邱伟华

（柳州职业技术学院，广西 柳州 545006）

只需要一个独立坐标，就可完全定义其几何位置的系统，就是单自由度系统，也就是最简单的、最基本的离散系统。实际工程中，很多简单系统可以简化为单自由度系统，例如简单弹簧和质量系统。当我们对只包含惯性元件和弹性元件的系统，不考虑阻尼进行讨论，这就是最简单的单自由度无阻尼系统。

笔者介绍了单自由度弹簧质量系统固有频率的计算方法，并依靠不同的方法，比较了忽略弹簧自身质量以及考虑弹簧自身质量对于固有频率的影响。

1 无阻尼弹簧质量系统的自由振动[1]

如图1所示，就是本文要讨论的单自由度无阻尼系统。

图1 弹簧质量系统及简化坐标

该系统有质量为m的重物（惯性元件）和刚度为k的弹簧（弹性元件）组成。假设不考虑重物的尺寸效应，可以用一个简单质点来表示这一类重物。为了描述图示系统位置，采用如图1所示的单轴坐标系。坐标原点选取在质点静平衡位置，用x表示质点在任意时刻处于坐标系中的坐标，以向下的方向为正。在此系统运动过程中，x 是时间t的函数，可以称为质点的位移函数。由于只需要一个空间坐标x，就可以完全确定图中质点任意时刻的位置，因此可以认为该系统就是单自由度系统。不考虑阻尼的情形下，系统将在初始条件激励下，围绕静平衡点做无阻尼自由振动。

2 振动方程的建立方法[2]

对于简单系统，振动微分方程的建立主要有2种方法。本文首先进行不考虑弹簧自身质量情形下的微分方程建立方法。

2.1 用牛顿第二定律法建立微分方程

牛顿第二定律又称运动定律，即物体动量的改变与施加的力量成正比。对于图示系统，定义质点的静平衡位置为坐标原点，则质点与坐标原点O的距离为x，可得作用在质点上的弹簧力为[3]

式中，

ξs=mg/k表示弹簧在重物作用下的静伸长，符号表示力fs的方向始终与（x +ξs）的方向相反，其作用是始终试图恢复弹簧的原长，一般称为弹性恢复力。

又由牛顿第二定律有

上两式运算结果得

式（3）就是图1所示单自由度无阻尼系统的自由振动微分方程，其是一个二阶线性常系数齐次微分方程。为了使得图1所示系统产生自由振动，需要有一个初始激励，或者说系统应该有一个非零的初始状态。初始激励，也就是初始扰动，通常由t=0 时刻的位移和速度来表示，即为

2.2 用能量法建立系统微分方程

对于本文讨论的假设情形无阻尼状态，那么可以认为是不存在能量耗散，也不会对外提供额外能量，那么系统的机械能是守恒的。机械能守恒的数学表达式为

式中，

Tmax为系统动能最大值；

Umax为系统势能最大值；

等式含义即是系统的动能最大值等于势能的最大值。

在此还有另一种表达方式

求导后有

根据图1的弹簧质量体系，若把坐标原点选在质点的静平衡位置，选择质点m的任意时刻坐标为x，可以求得任意时刻系统动能为

假定系统在静平衡的位置作为势能零点，对于质点m 处于x位置时刻的系统势能为

把T 和U 代入（7）可得：

即获得和式（3）相同的微分方程。

因此，可以得出结论，即使使用方法的不同，不影响同一系统具有相同的运动微分方程。

3 运动微分方程的求解

通过上边的微分方程建立，可知同一系统的运动微分方程具有唯一形式，下边将对此微分方程进行求解。

3.1 振动微分方程的求解与振动特性分析

这是一个常系数微分方程，可以直接解出。假设方程（3）具有如下形式的特解

代入式（13）得

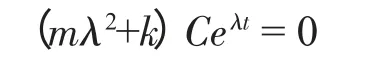
由于系统的振动位移不恒等于零，因此可得

此式即为式（3）的特征方程。解方程易得

此式中

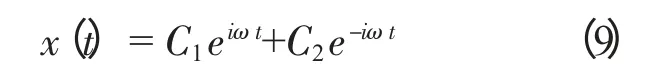
由特征根可以得到式（3）的通解为此式即为质点任意时刻的运动轨迹方程的复数表达方式，式中C1和C2均为待定常数。为了更清楚看出运动的特点，可以用欧拉公式进行转化，以三角函数来表示运动的轨迹。根据欧拉公式代入式（9）并整理有[4]

由于C1和C2均为待定常数，而且C1和C2必须为一对共轭复数，进一步整理得

式中，C 和D 均为待定常数，进一步三角变化得

式中的A 和φ 均为由初始条件确定的待定常数。

此时可以看出，本文讨论的质量体系的运动方式为一个以A为振幅，以ω为固有频率，以φ为初始相位的无阻尼简谐振动。其中

即为简谐振动的固有频率。

必须强调，以上计算都是以忽略弹簧自身质量作为基础的。

3.2 考虑弹簧自身质量情况下的固有频率计算

一般的理论力学考虑中，弹簧自身质量都是不予考虑的。但是在实际工程中，大型弹簧的实际质量很大，在固有频率的计算中，忽略弹簧自身质量之后的影响非常大，因此有必要给出考虑弹簧自身质量之下的弹簧质量系统固有频率的计算结果，并和理想状况下的固有频率进行对比。

方程的建立，使用能量法。

如图2所示，可设弹簧长度为l，单位长度的质量为ρ，坐标原点选在系统静平衡处，当弹簧端点的位移是x的时候，静平衡时刻距离固定支点端距离为s 处，弹簧位移为sx / l，此处的质量为ρds。

图2 考虑弹簧质量情况下的计算

此时可知，弹簧的动能为

则系统的总动能为

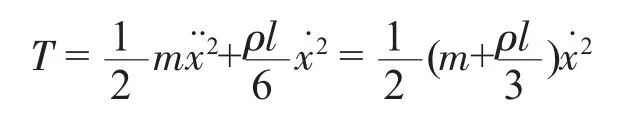
而系统的总势能为

根据式（7）

以及微分方程求解如文中第3 节计算得考虑了弹簧质量情况下的弹簧质量系统的固有频率

4 结束语

由上边计算可以知道，在实际工程中，一旦考虑了弹簧的自身质量，那么简单弹簧质量系统的固有频率对比不考虑弹簧自身质量的理想结果，实际中的固有频率，是低于忽略弹簧自身质量的理想结果的。

[1]诸德超，邢誉峰.工程振动基础[M].北京：北京航空航天大学出版社，2005.

[2]（美）Singiresu Rao.机械振动[M].李欣业，张明路，译，北京：清华大学出版社，2009.

[3]尹冠生理论力学[M].西安:西北工业大学出版社，2004.

[4]陈宗煊，刘名生.复变函数[M].北京：科学出版社，2010.