☉贵州省龙里中学 洪其强（特级教师）

高中“数学情境与提出问题教学实践”与启发式教学
——“圆锥曲线与对称问题”的教学案例

☉贵州省龙里中学 洪其强（特级教师）

教学目的：

1.引导学生探索并掌握中心对称及轴对称问题的解决方法.

2.通过对称问题的研究求解，进一步理解数形结合的思想方法，提高分析问题和解决问题的能力.

3.通过对称问题的探讨，使学生进一步会运用运动变化的观点，用化归的思想处理问题.

教学重点：

两曲线关于定点和定直线的对称问题.

教学难点：

把数学问题转化为对称问题，即用对称的观点解决实际问题是难点.

教学过程：

师：前面学过了几种常见的曲线方程，并讨论了曲线的性质.今天这节课继续讨论有关对称的问题.大家想一想：点P1（x1，y1）、P2（x2，y2）关于点Q（x0，y0）对称，那么它们的坐标应满足什么关系？

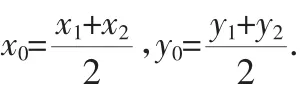
师：点P1（x1，y1）、P2（x2，y2）关于原点对称，那么它们的坐标又满足什么关系？

生：P1和P2的中点是原点.即x1=－x2，且y1=－y2.

师：若P1和P2关于x轴对称，它们的坐标又怎样呢？

生：x1=x2，且y1=－y2.

师：若P1和P2关于y轴对称，它们的坐标有什么关系？

生：x1=－x2，且y1=y2.

师：若P1和P2关于直线y=x对称，它们的坐标又会怎样？

生：y1=x2，且x1=y2.

师：若P1和P2关于直线y=x+a对称，它们的坐标又会怎样？

生：y1=x2+a，且x1=y2－a.

师：若P1和P2关于直线y=－x对称，它们的坐标又会怎样？

生：y1=－x2，且x1=－y2.

师：若P1和P2关于直线y=－x+a对称，它们的坐标又会怎样？

生：y1=－x2+a，且x1=－y2+a.

师：下面哪位同学来归纳一下，P1和P2关于点以及上述有关的对称问题？

生：横变纵不变，关于y轴对称；纵变横不变，关于x轴对称；横纵都变负，关于原点对称；横纵都互换，关于y=x对称.

生：它们关于直线y=x对称.

师：若点P1和点P2关于直线Ax+By+C=0对称，那么它们的位置有何关系？

生：点P1和点P2必须在直线Ax+By+C=0的异侧.

师：还有吗？

生：P1P2的连线一定与直线Ax+By+C=0垂直.

师：点P1和点P2在直线Ax+By+C=0的异侧且与直线垂直就能对称了吗？

生：还需要保证点P1和点P2的中点落在直线Ax+By+C=0上，也就是说P1和P2的中点坐标满足直线方程Ax+By+C=0.

师：下面哪位同学来归纳一下，两点P1和P2关于直线Ax+By+C=0对称应满足的条件？

生：应满足两个条件.第一个条件是P1P2的连线垂直于直线Ax+By+C=0，第二个条件是P1和P2的中点应落在直线Ax+By+C=0上.

师：这两个条件能否用方程表示呢？（在黑板上可画出图形，以示直观）

生：设P（x，y），则P点关于直线Ax+By+C=0的对称点为P′（x1，y1），其方程组为：

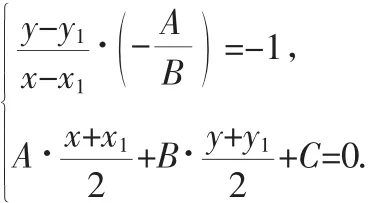
师：这个方程组说明了什么？它能解决什么问题？

生：方程组中含有x1和y1，也可认为这是一个含x1和y1的二元一次方程组．也就是说，给定一个点P（x，y）和一条定直线Ax+By+C=0，可以求出P点关于直线Ax+By+C=0的对称点P′（x1，y1）的坐标．

师：今后有很多有关对称的问题都可以用此方法处理，很有代表性．但也还有其他方法，大家一起看下面的例题．

例1 已知直线l1和l2关于直线2x－2y+1=0对称，若l1的方程是3x-2y+1=0，求l2的方程．

（选题目的：熟悉对称直线方程）

师：哪位同学能谈谈？

生：先求出已知两直线的交点，设l2的斜率为k，由两条直线的夹角公式可求出k，再用点斜式求得l2的方程．

（让这位同学在黑板上把解题的过程写出来，大家订正）

师：还有别的解法吗？

生：在直线l1上任取一点，求出这点关于2x－2y+1=0对称的点，然后再利用两点式可求出l2的直线方程．

（让这位学生在黑板上把解题过程写出来，如有错误，大家订正）

师：还有别的解法吗？

生：在l2上任取一点P（x，y），则P点关于2x-2y+1=0对称的点P′（x′，y′）在l1上，列出方程组，解出x′、y′，代入l1，问题就解决了．

师：请你到黑板上把解题过程写出来．

生：解：设P（x，y）为l2上的任意一点．

则P点关于直线2x－2y+1=0对称点P′（x′，y′）在l1上．

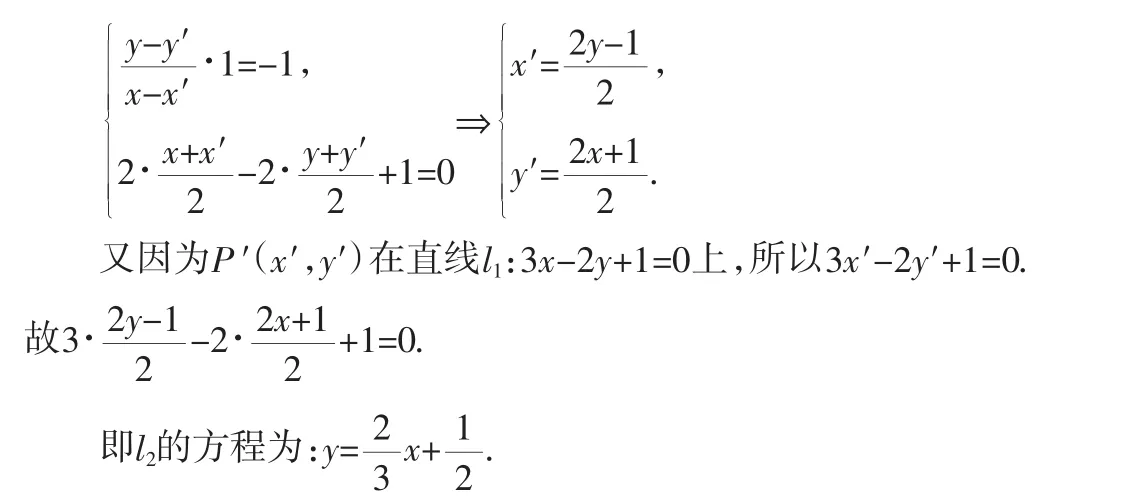
师：很好，大家刚才的几种解法是求对称直线方程的常规方法．那么，如果把l1改为曲线，怎样求曲线关于一条直线对称的曲线方程呢？

推广：已知曲线C：f（x，y）=0，求它关于直线x-y-2=0对称的曲线方程．

（选题目的：进一步熟悉对称曲线方程的一般方法）

师：例1中的几种解法还都适用吗？

生：第二种和第三种方法还能适用．

师：谁来试一试？

生：可先在曲线C：f（x，y）=0上任取一点P0（x0，y0），它关于直线的对称点P ′（x1，y1），可得直线P0P ′与x-y-2=0的交点，从中解出x0、y0，代入曲线C：f（x，y）=0即可．

（让学生把他的解法写出来）

解：设P0（x0，y0）是曲线C：f（x，y）=0上任意一点，它关于直线x-y-2=0对称的点为P′（x1，y1），因此，连接P0（x0，y0）和P′（x1，y1）两点的直线方程为y-y0=-（x-x0）．

师：还有不同的方法吗？

生：用两点关于直线对称的方法也能解决．

师：把你的解法写在黑板上．

生：解：设M（x，y）为所求的曲线上任一点，M0（x0，y0）是M关于直线x-y-2=0对称的点，所以M0定在曲线C：f（x，y）=0上．

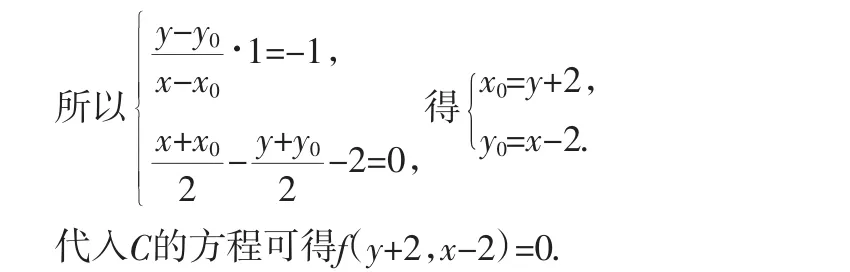
师：大家再看一个例子．

例2 已知点A（0，4）和圆C：（x－9）2+（y－8）2=16，一条光线从A点出发射到x轴上后，沿圆的切线方向反射，求这条光线从A点到切点所经过的路程．（如图1）

师：解这道题的关键是什么？

生：关键是找到光线与x轴的交点．

师：有办法找到交点吗？

（没人回答）

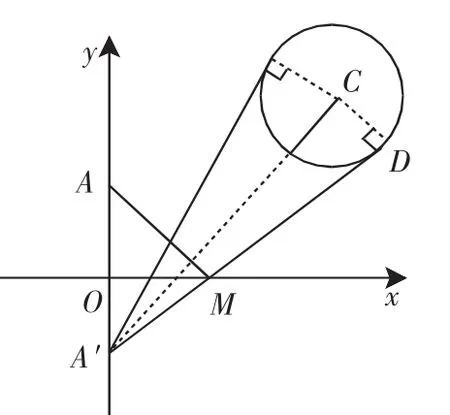
图1

师：交点不好找，那么我们先假设M就是交点，利用交点M对解决这个问题有什么帮助吗？

生：既然AM是入射光线，MD为反射光线，D为切点，这样入射角就等于反射角，从而能推出∠AMO=∠DMx.

（让这位学生把解答写在黑板上）

师：巧用对称性，化简了计算，很好.哪位同学能把这个题适当改一下，变成另一个题目？

师：谁能解答这个问题？

生：先作点M（－3，0）关于直线l：x－y+9=0的对称点M′（－9，6），连接M′N并延长交l于一点，易证该点即是所求的点P.

师：这题还能不能再做些变形，使之成为另一个题目？

师：哪位同学能够解决？

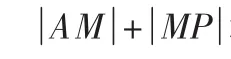
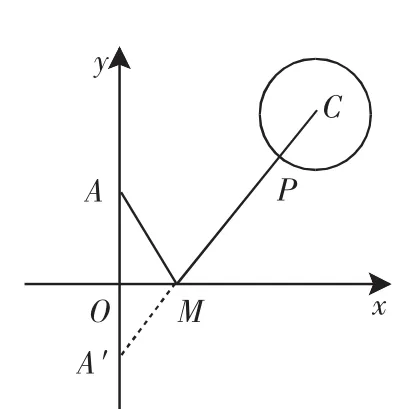
图2

师：你怎样想到先找A点关于x轴的对称点A′的呢？

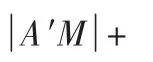
师：很好，大家一起动笔算一算（同时让这位学生上前面书写）.

师：我们一起看下面的问题.

例3 若抛物线y=ax2－1上总存在关于直线x+y=0对称的两点，求a的范围.

师：这题的思路是什么？

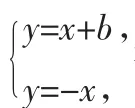
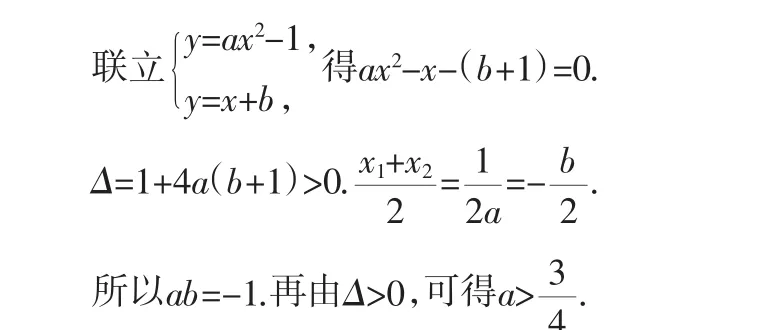
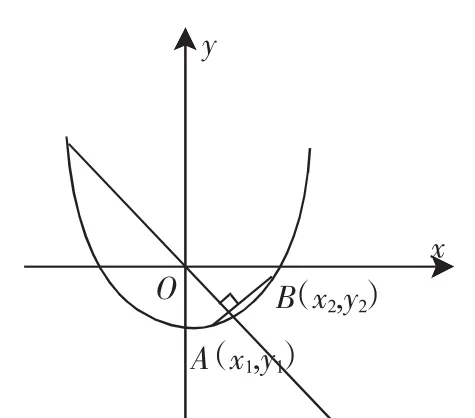
图3

师：很好，谁还有不同的解法吗？

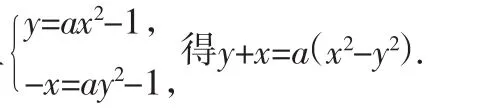
师：今天我们讨论了有关点、直线、曲线关于定点、定直线对称的问题.解决这些问题的关键所在就是牢固掌握灵活运用两点关于定直线对称的思想方法，结合图像利用数形结合思想解决问题.

作业：

1.一个以原点为圆心的圆与圆：x2+y2+8x－4y=0关于直线l对称，求直线l的方程.

2.四边形ABCD是平行四边形，已知点A（－1，3）和C（－3，2），点D在直线x－3y－1=0上移动，则点B的轨迹方程是______.

3.若光线从点A（－3，5）射到直线3x－4y+4=0之后，反射到点B（3，9），则此光线所经过的路程的长是______.

4.已知曲线C：y=－x2+x+2关于点（a，2a）对称的曲线是C′，若C与C′有两个不同的公共点，求a的取值范围.

设计说明：

1.这节课是一节专题习题课，也可以认为是复习题，通过讨论对称问题把有关的知识进行复习，最重要的是充分突出以学生为主体．让学生讨论和发言，就是让学生参加到数学教学中来，使学生兴趣盎然，思维活跃，同时对自己也充满了信心．这样，才有利于发挥学生的主动性，有利于培养学生独立思考的习惯，发展学生的创造性和思维能力．因此，在数学教学中，要有一定的时间让学生充分地发表自己的见解，从而来提高他们的兴趣，发展他们的能力．

2．这节课自始至终贯穿数形结合的数学思想，让学生在脑海里留下一个深刻的印象，对称问题归根结底都可以化成点关于直线的对称问题，即可用方程组去解决．反过来，一直线与一曲线的方程组消元后得到一元二次方程，若这个二次方程的判别式大于0，也可得直线与曲线有两个交点，这种从形到数，再由数到形的转化为我们处理解析几何问题带来了便利．在解题时，只有站在一定的高度去处理问题，思路才能开阔，方法才能灵活，学生的能力才能真正的得到培养，同时水平才能提高得较快．

3．习题课的一个中心就是解题，怎样才能让学生做尽可能少的题，从而让学生掌握通理通法，这是一个值得研究和探讨的问题．本节课采取了让学生把题目进行一题多变，一题多解，从中使学生悟出一些解题办法和规律，从而达到尽可能做少量的题，而达到获取尽可能多的知识、方法和规律的目的，真正提高学生分析问题、提出问题、解决问题的能力，解决当前学生课业负担过重的问题，根除题海战术给学生带来的危害．

4．本课的例题可根据自己所教学生的实际情况进行选择，下面几个备用题可供参考．

题目1 过圆O：x2+y2=4与y轴正半轴的交点A作这圆的切线l，M为l上任一点，过M作圆O的另一条切线，切点为Q，求点M在直线l上移动时，△MAQ的垂心的轨迹方程．

（选题目的：熟练用代入法求动点的轨迹方程，活用平面几何简化计算）

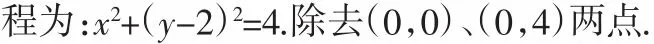
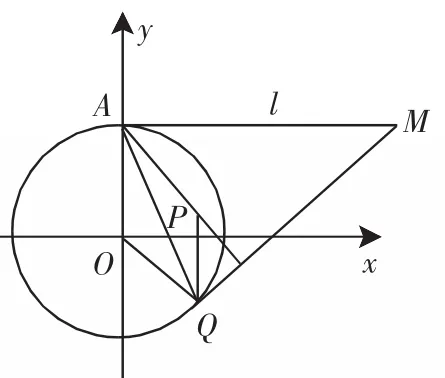
图4

题目2 若抛物线y=x2上存在关于直线y=m（x－3）对称的两点，求实数m的取值范围．

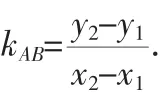
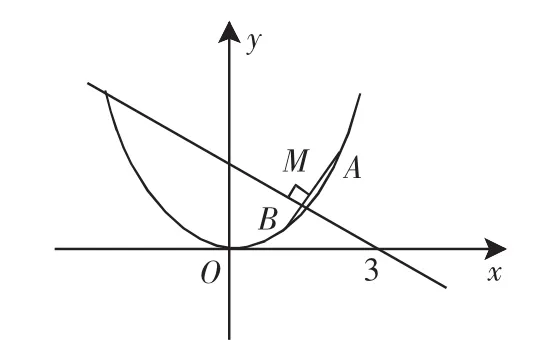
图5

（选题目的：结合对称问题，训练反证法的应用）

此题证法很多．下面给出一种证法，供参考．

证明：如图6，若P、Q两点关于y=x对称，可设P（a，b）、Q（b，a）且a≠b，a、b∈R．

由P、Q在抛物线上，得

图6

其判别式Δ=4－8＜0，所以a∉R，这与题设矛盾，说明P、Q两点不存在．