梁海华,吴奎霖

(1.广东技术师范学院计算机科学学院,广东广州 510665; 2.中山大学数学与计算科学学院,广东广州 510275)

一类三次系统的正规形和无环性

梁海华1*,吴奎霖2

(1.广东技术师范学院计算机科学学院,广东广州 510665; 2.中山大学数学与计算科学学院,广东广州 510275)

研究了具有次数不超过3的多项式倒积分因子的三次平面微分系统，给出了这类系统的正规形并证明了这类系统不存在极限环.

倒积分因子; 三次系统; 正规形; 极限环

近年来,很多文献研究了具有不变代数曲线或具有Darboux型首次积分的二次系统的拓扑性态,见文献[1]、[2]及其参考文献.研究相应的三次系统的文献则很少.本文研究一类三次平面多项式微分系统

(E3)

的正规形并讨论它是否存在极限环.为此,首先阐述一些基本概念和本领域的一些基本成果.

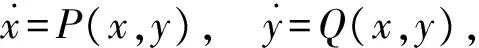
(1)

如果存在上述开集U及定义在其上的不恒为常数的连续可微函数R使得X(R)=-divX·R,则称R是系统(1)的一个积分因子.利用积分因子往往能够构造出首次积分.如果1/V是系统(1)的一个积分因子,则称V是系统(1)的一个倒积分因子.简单计算可以看出,V是系统(1)的倒积分因子当且仅当X(V)=divX·V在U上恒成立.

对于一个多项式系统而言,代数曲线的存在性是十分重要的.例如,任一m次多项式系统(1),如果存在m(m+1)/2条线性无关的不可约的不变代数曲线,则该系统一定是Darboux可积的.详细情形见文献[3](最近文献[4]把文献[3]的结论推广到n维仿射空间).另一个重要的结论是,利用一个已知的不变代数曲线,可以得到系统的正规形,见下面的命题.

命题1[5]假定C=0是m次多项式系统(1)的不可约的不变代数曲线,c=degC,且C的c次齐次项没有重因子,则系统(1)具有如下正规形:

其中A、B和D是适当的多项式,满足degA,degB≤m-c,degD≤m-c+1.

有趣的是系统(1)的倒积分因子也是该系统的不变代数曲线并以Px+Qy作为其余因子.这种具有特殊的代数曲线的多项式系统引起了人们极大的兴趣[6].文献[7]证明了：

命题2 令V是系统(1)的倒积分因子,则系统(1)的极限环(如果存在的话)必含于代数曲线∑={(x,y):V(x,y)=0}中.

利用这个命题来判断具有倒积分因子的多项式系统是否存在极限环(若存在,是否唯一)显然是十分方便的.我们给出一个简单的例子.

例1 系统

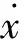
具有倒积分因子V=(x2+y2)(x2+y2-1).不难看出x2+y2=1是该系统的极限环.因此该系统具有唯一的一个极限环x2+y2=1.

本文将讨论具有次数不超过3的不可约多项式倒积分因子的三次系统(E3),确定这类系统的正规形并证明这类系统不存在极限环.这里所说的正规形是指在仿射变换下,必要时可以改变时间的尺度,使得系统可以化为该(正规)形式.顺便指出,文献[8]探讨了二次多项式系统的正规形,而文献[9]证明了一类具有特殊结构的二次多项式系统不具有极限环,因此本文的结果是对这方面的一个拓展.

1 系统(E3)的正规形

假定V(x,y)是系统(E3)的一个不可约的倒积分因子,且degV≤3.我们将根据V(x,y)的次数来确定系统(E3)的正规形,使得系统(E3)仿射等价于该正规形.根据文献[10]、[11],任一不可约的三次平面多项式经过仿射变换后,可以化为如下4种形式:

(A3)ax3+xy2+bx2+cx+dy+e;

(B3)ax3+bx2+y2+cx+d(a≠0);

(C3)ax3+xy+bx2+cx+d(a≠0);

(D3)ax3+bx2+cx+y+d(a≠0).

任一不可约的二次多项式经过仿射变换后总能化为如下4种形式:(A2)x2+y2+1(复单位圆);(B2)x2+y2-1(实单位圆);(C2)xy-1(双曲抛物线);(D2)y-x2(抛物线).而任一一次多项式经过仿射变换后总能化为x+c.

本节的主要结论是如下定理:

定理1 设系统(E3)具有一个不可约的多项式倒积分因子,则

(a)如果该倒积分因子是三次多项式,则系统(E3)具有如下正规形

(2)

其中V是(A3)～(D3)中的一个,而r,s和m是常数且r2+s2≠0;

(b)如果该倒积分因子是二次多项式,则系统(E3)具有如下正规形

(3)

其中V是(A2)～(D2)中的一个,而r,m,n,k,l,a是常数且a2+n2+m2≠0;

(c)如果该倒积分因子是一次多项式,则系统(E3)具有如下正规形

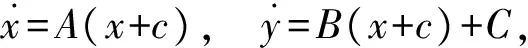
(4)

其中A,B是关于x,y的二次多项式,C是关于x的三次多项式.

证明作为系统(E3)的倒积分因子,V满足X(V)=divX·V,即

P(x,y)Vx(x,y)+Q(x,y)Vy(x,y)=

(Px(x,y)+Qy(x,y))V(x,y).

根据地理学内容，可将地理国情监测划分为2个方面，基础性地理国情监测和专题性地理国情监测，以便最真实客观地反映自然地表及人文地理的现状。地理国情监测具体内容延续普查时期的内容体系，利用符合监测时点和分辨率的卫星影像，收集民政、国土、环保、建设、交通、水利、农业、统计、林业等最新版专题资料，采集变化信息，同时结合外业核查结果，补充新增和变化内容，使各类要素的现势性符合当年的真实状态，形成覆盖全国的时间序列数据成果。

(5)

首先证明(a).不失一般性,我们设系统(E3)的不可约的三次多项式倒积分因子V已经是(A3)～(D3)中的一个,并依照这4种形式来证明.

(1)V=ax3+xy2+bx2+cx+dy+e.

如果a≠0,则V的最高次齐次项ax3+xy2没有重因子.根据命题1,系统(E3)经过仿射变换后可以化为

这里L=mx+ny+k,r,s,m,n,k是实数.

把P=rV-LVy,Q=sV+LVx代入式(5)得到

(rV-LVy)Vx+(sV+LVx)Vy=[(r+n)Vx+(s-m)Vy]V,

从而nVx=mVy.由于V的最高次齐次项ax3+xy2没有重因子,所以(Vx,Vy)=1(见文献[5]的引理5).故m=n=0.于是系统(E3)具有正规形(2).

如果a=0,即V=xy2+bx2+cx+dy+e,则分为b=0及b≠0这2种情况来讨论.

a03=a02=a21=a30=b30=b11=b03=b21=0,

a00=-b02d+a20e,a01=a20d,a12=a20,

a11=-2b02,a10=a20c,

b20=b12,b01=b12d,b10=2b02+b12c,b00=b02c+b12e.

由此,系统(E3)可以写为

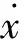
这就是正规形(2).对于b<0的讨论完全类似,此处从略.

(ii)b=0.此时V=xy2+cx+dy+e.如果d≠0,则把V=xy2+cx+dy+e代入式(5)，得

a02=a03=a30=a20=a21=b20=b11=b30=b21=b03=0,

a12=a01/d,a10=a01c/d,a00=-b02d+a01e/d,

a11=-2b02,b00=b02c+b12e,b10=b12c,b01=b12d.

故系统(E3)可以写为正规形(2):

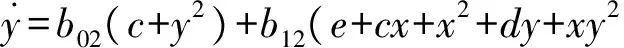
如果d=0,即V=xy2+cx+e,则e≠0,否则V是可约多项式.类似前面的分析可得

b00=b02c+b12e,b10=b12c,a10=a00c/e,

a11=-2b02,a12=a00/e,

且系统(E3)的其他系数全部等于零.这时系统(E3)可以化为正规形(2):

证毕.

(2)V=ax3+bx2+y2+cx+d.

b00=-a01c/2c+b02d，b10=b02c,

b20=-3a01/2,a00=a30d,a02=a30,

而系统(E3)的其他系数为零.这样,系统(E3)变为

这就是正规形(2).

(3)V=ax3+xy+bx2+cx+d.

b00=b01c+b11d,b10=2bb01+b11c,b20=3b01+bb11,

b30=b11,a10=-b01+a30c,a11=a30,a20=a30b,a00=a30d,

而系统(E3)的其他系数为零.这样,系统(E3)化为正规形(2):

(4)V=ax3+bx2+cx+y+d.

b30=b01,b00=b20c/3,b10=b01c,

a01=a30,a00=-b30/3,a10=a30c.

故系统(E3)变为正规形(2):

(6)

最后,注意到系统(E3)是三次系统,所以在正规形(2)中必有r2+s2≠0.这就完成了(a)的证明.

其次证明(b).不失一般性,设系统(E3)的不可约的二次多项式倒积分因子V已经是(A2)～(D2)中的一个,并依照这4种形式来进行证明.

(1)V=x2+y2+1.

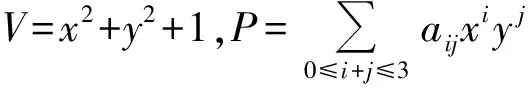
-a10-b01=0,-a11+2b00-2b02=0,

-a10-a12+b01-3b03=0,

-a11=0,-a12-b03=0,2a00-2a20-b11=0,

a01-a21+b10-b12=0,

2a02-2a20+b11=0,a03-a21=0,

a10-3a30-b01-b21=0,-a30-b21=0,

a11-2b02+2b20=0,a12-3a30-3b03+b21=0,

-b11=0,b12-b30=0.

化简得

a00=a20,a01=a21-b10+b30,a02=a20,

a03=a21,a10=-b21,a11=0,a12=-b21,a30=-b21,

b00=b20,b01=b21,b02=b20,b03=b21,b11=0,b12=b30.

代回系统(E3)就可以得到

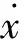
这就是正规形(3).其他情形(B2)～(D2)的讨论完全类似,此处从略.

a00=c(a10+b11c-b21c2),a01=c(a11+2b12)c,

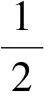
代回系统(E3),得

2b21cx+b21x2-2a11y-4b12cy+4b12xy-2a12y2),

这就是正规形(4).证毕.

2 系统(E3)的无环性

这一节将证明,当三次系统(E3)具有次数不超过3的不可约多项式倒积分因子V时,它一定不存在极限环.已有文献在讨论类似的问题时往往是以命题2作为主要工具,即假定所考虑的系统存在极限环,则该环必含于V=0中.因此V=0必须含有闭曲线.应用到我们所讨论的问题,对于degV=2,不失一般性可设V=x2+y2-1.对于degV=3,根据文献[12],任一含有闭曲线的三次代数曲线可以化为(经过仿射变换)

(7)

故不失一般性可设V具有式(7)左端的形式.然后分别证明degV=2及degV=3时V=0不是该系统的闭轨线,从而系统(E3)不存在极限环.然而这种方法在讨论过程中比较繁琐,故我们不打算采用之.另一方面,对于任一平面微分系统,只要其存在不恒为常数的解析的首次积分,则该系统不存在极限环.事实上,假设该系统存在极限环γ,则可在γ附近找到一条轨线γ1,使得γ1无限缠绕而趋于γ.设系统的首次积分是H.由于H解析,所以H(γ1)可以无限地接近H(γ).这矛盾于H(γ)和H(γ1)是2个不同的常数.在下面的讨论中,我们将使用这一原理以及定理1来证明系统不存在极限环.为此首先证明下面的引理.

引理1 假设系统(1)存在一个解析的倒积分因子V.此外,存在实数r以及定义在2上、不恒为常数的实值解析函数B(x,y),使得X(B)=r·divX,即

P(x,y)Bx(x,y)+Q(x,y)By(x,y)=

r(Px(x,y)+Qy(x,y))，

(8)

则系统(1)不存在极限环.

证明如果r=0,则

X(B)=P(x,y)Bx(x,y)+Q(x,y)By(x,y)≡0.

如果r≠0,令

则H在2上解析.根据式(8)得

下面证明本节的主要定理：

定理2 假设系统(E3)有一个次数不超过3的不可约的多项式倒积分因子V,则系统(E3)不存在极限环.

证明当degV=1时,根据命题2以及V(x,y)=0不可能包含闭曲线可看出定理的结论是成立的.

当degV=2时,根据定理1,系统(E3)具有正规形(3).

令B(x,y)=ny2-mx2+2axy-2lx+2ky.直接计算得

X(B)=P(x,y)Bx(x,y)+Q(x,y)By(x,y)=

r(Px(x,y)+Qy(x,y)),

其中P(x,y)=(ax+ny+k)V-rVy,Q(x,y)=(mx-ay+l)V+rVx.由引理1,系统(E3)不存在极限环.

当degV=3时,系统(E3)具有正规形(2).

令B(x,y)=2ry-2sx,则

X(B)=P(x,y)Bx(x,y)+Q(x,y)By(x,y)=

m(Px(x,y)+Qy(x,y)),

其中P(x,y)=rV-mVy,Q(x,y)=sV+mVx.由引理1,系统(E3)不存在极限环.证毕.

[3] DARBOUX G.Mémoire sur les équations différentielles algébriques du premier ordre et du premier degré[J].Bull Sci Math,1878,2:60-96.

[4] LLIBRE J,ZHANG X.Darboux theory of integrability inntaking into account the multiplicity[J].J Diff Eqns,2009,246:541-551.

[5] CHRISTOPHER C,LLIBRE J,PANTAZI C,et al.Darboux integrability and invariant algebraic curves for planar polynomial systems[J].J Phys A:Math Gen,2002,35:2457-2476.

[6] CHAVARRIGA J,GIACOMINI H,GINÉ J,et al.Darboux integrability and the inverse integrating factor[J].J Diff Eqns,2003,194:116-139.

[7] GIACOMINI H,LLIBRE J,VIANO M.On the nonexistence,existence and uniqueness of limit cycles[J].Nonlinearity,1996,9:501-516.

[8] GASULL A,REN S,LLIBRE J.Chordal quadratic systems[J].Rocky Mountain J of Math,1986,16:751-782.

[9] ARTÉS J C,LLIBRE J.Nonexistence of limit cycles for a class of structurally stable quadratic vector fields[J].Disc Contin Dyn Sys,2007,17:259-270.

[10] BRIESHORN E,KNRRER H.Plane algebraic curves[M].Basel:Birkhauser,1986.

[12] HOROZOV E,ILIEV I D.On the number of limit cycles in perturbations of quadratic Hamiltonian systems[J].Proc London Math Soc,1994,69:198-224.

Keywords： inverse integrating factor; cubic system; normal form; limit cycle

【责任编辑 庄晓琼】

NORMALFORMANDNONEXISTENCEOFLIMITCYCLEOFACLASSOFCUBICSYSTEM

LIANG Haihua1*,WU Kuilin2

(1.Department of Computer Science,Guangdong Polytechnic Normal University,Guangzhou 510665,China;2.Department of Mathematics,Sun Yat-Sen University,Guangzhou 510275,China)

A planar cubic differential system with an inverse integrating factor,whose degree is no larger than 3,is investigated.The normal form of this system is given and it is proved that this system has no limit cycles.

2010-09-01

国家自然科学基金项目(10871214);广东省自然科学基金项目(9151008002000012)

*通讯作者,haiihuaa@tom.com

1000-5463(2011)02-0028-05

O175.12

A