寇惠敏，孟昭为

(山东理工大学理学院，山东 淄博 255049)

由于金融资产(特别是股票和外汇)的交易价格一般具有“时间连续性”，因此，金融资产的收益率应该是平稳的。但是，随着日内高频交易数据的可用性，许多学者发现，金融资产的收益率在日内近似连续的时间内有可能出现大幅波动，这种现象称为“跳跃”。跳跃在金融资产收益波动率的估计和预报中具有非常重要的意义。在金融计量经济学中对带有跳跃项的随机波动率模型的研究是一个重要的课题，模型中过高的峰度等一般都是由收益和波动中的跳跃引起的，而用简单的SV模型无法解释。在Eraker的文章中曾讲过研究带有跳跃的SV模型的重要性和实用性。

本文在收益和波动中的跳跃项带同期性和相关性的随机波动率模型的基础上，用LM乘子检验，验证了在波动中跳跃的存在性，利用的是狄拉克·δ函数的思想推导出方差无限小的跳跃项密度函数，这个方法是kobayashi和Shi提出的，用它去处理在原假设下退化的密度函数。

1 基本SV模型

基本形式:

其中:ut～ N(0，1);νt～N(0，1);|β|＜1;ut与 νt相互独立。可以求出 yt与 θt的条件密度函数

状态变量的初始值θ0通常假设为服从，或者假设为一个固定值。前一个假设中状态变量是稳定的，后一种情况，θ0的密度的均值和方差均退化成零，可以看成是狄拉克·δ函数。在这2种情况下，都用h0(θ0)表示θ0的密度函数。

基本 SV 模型的密度函数可以通过 θ0，θ1，…，θT和 y1，…，yT的联合密度函数表示出的 θ0，θ1，…，θT获得，可以表示为

此后，为书写上的方便，积分区间(－∞，+∞)可省略，用dθ代表n个参数的积分符号dθ0dθ1…dθT。

2 在收益方程中带有跳跃项的SV模型

假设在收益方程中跳跃发生的概率为p，跳跃的大小服从独立的正态分布，其中均值为0，方差为λ。跳跃变量et的分布是一个正态分布和一个0向量合成的，权重分别为p和1－p，其中0向量表示所有的点在0处都等于0的退化分布。可以写成:

其中，0＜p＜1，跳跃的发生和ut，νt是独立的，这个模型叫做SVJ模型，由 Eraker等提出。用测量和变换方程表示成非线性状态空间模型的形式

它们的条件密度函数可以写成

那么，在收益方程中，带有跳跃项的y1，…，yT的密度函数可表示为

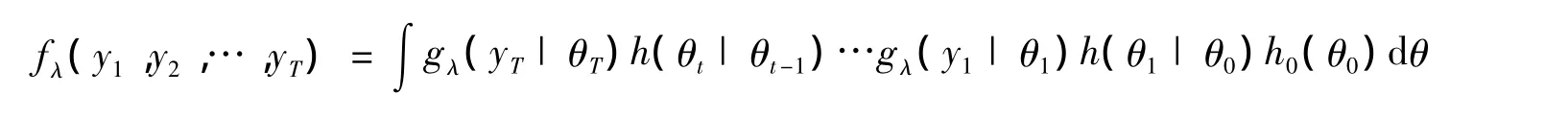
3 在波动和收益方程中跳跃项的相关性和同期性检验

在假设跳跃在收益和波动方程中同时发生的情况下，推导出一种新的拉格朗日乘子检验法，并用该方法去检验在波动方程中的跳跃项。原假设为在收益方程中含有跳跃项的SV模型，被择假设为在收益和波动方程中含有相关的跳跃项的SV模型，后者记为SVCJ模型。

在波动和收益方程中，含有同期性和相关性的随机波动率模型可以表示为

假设在波动和收益方程中跳跃ηt，et同时发生的概率为p，跳跃发生的条件是这些跳跃满足二元正态分布，且ηt＞0。在波动方程中跳跃项的边缘分布是一个半正态分布，即正态分布的正向部分。按照传统的假设，波动方程中的跳跃项不能为负，但本文做了一些改动，因为用到的模型中是原先情况的扩展，所以波动方程中的跳跃项可以是负的。

波动和收益方程中跳跃有条件发生时的联合概率密度函数为

其中:

ρ表示:2个跳跃项的相关性系数，当ρ＜0时，波动方程中的跳跃伴随着收益方程中的一个负的跳跃;当ρ＞0时，伴随着收益方程中一个正的跳跃。在检验统计量推导过程中，假设ρ≠0，因为若ρ=0，那么关于k的得分函数是恒等于0，就不能求出其检验统计量。收益方程和波动方程中震动的相关性也就是所谓的“杠杆效应”，在研究中是一个非常重要的问题。跳跃在t时刻发生时，θt和yt的条件联合密度函数表示为

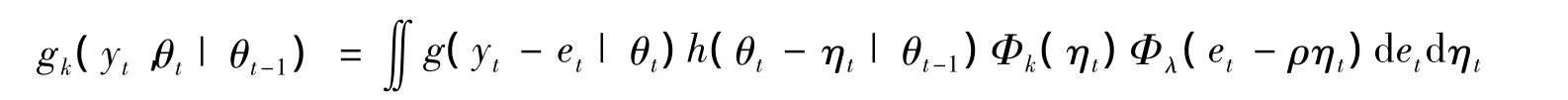
另一方面，在t时刻跳跃没有发生时，θt和yt的条件联合密度函数可以表示为

在收益和波动过程中含有相关跳跃项的y1，y2，…，yT的密度函数可以表示为

θt和yt的无条件联合密度函数表示为

测量和转移方程的密度函数 g(yt|θt)，h(θt|θt－1)可以分别由式(1)、(2)给出。

本文求SVJ模型在原假设下的LM检验统计量，即为在式(6)中的模型对备择假设含有未知参数α，β，σ2，λ，k，p，ρ的SVCJ模型。在原假设 k=0下，相当于 ηt≡0 。则，在原假设下，式(5)中的相关系数 ρ是不可辨认和不能估计的;但是，可以证明它对本文的LM检验统计量是没有影响的，因为在LM检验统计量中ρ可以忽略，所以检验统计量的分布对ρ来说是独立的。下面计算一阶导数。

第一，式(7)中已经给出了SVCJ模型的似然函数的形式，可以得到

而跳跃项关于k的条件联合密度函数的一阶导数是

则

此后，除非另有说明，所有的参数都是在k=0或ηt=0的条件下估计。可以得到

那么，在k=0时，y1，…，yt似然函数的一阶导数可以写成

其中de1，…，deT，缩写成de，它们的联合密度函数定义为

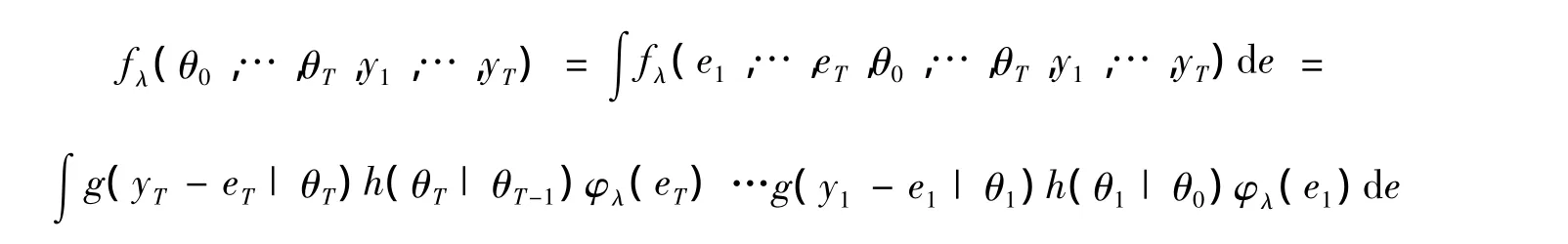
和

式(8)的第1项与方程成正比，定义为SVJ模型的σ2的最大似然估计并让它等于零，则

式(8)的第3项也为零，因为它与方程成正比例，定义为SVJ模型中参数λ的最大似然估计。因此，通过判断式(9)是否离零足够远，来检验假设k=0。

在收益方程中，跳跃项的条件密度函数定义为

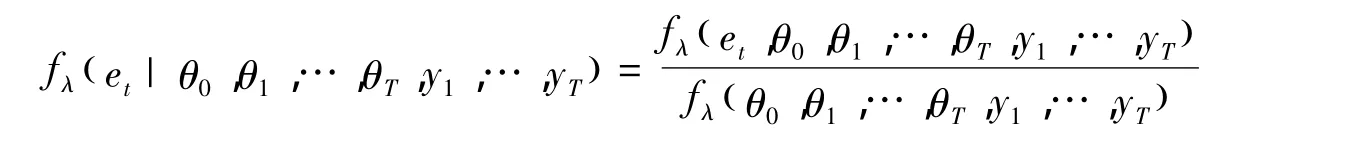
简写成

其中

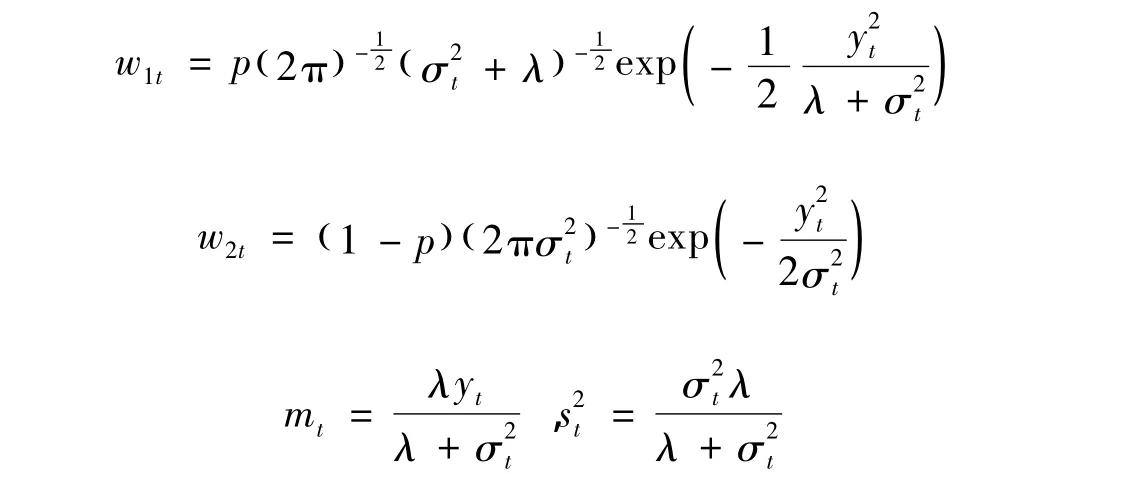
从而用式(10)在式(9)中表示出et，最后得到

上面用到在θt，yt给定的条件下，et的条件期望值是mtw1t/w1t+w2t，通过在y1，…，yT数值给定的条件下θ0，θ1，…，θT的条件密度函数可以计算出这个积分值，密度函数为式(4)给出的状态空间中SVJ模型代表的θ0，θ1，…，θT的平滑密度，这在Hamilton中已经给出了证明。

在这个问题上，构造了一个单边的LM检验:k=0对k＞0。起初，LM单边检验被定义为

其中S11是关于参数k，α，β，σ，λ，p的Fisher信息阵的逆的第(1，1)的元素。估计Fisher信息阵S也就是得分函数的标准误差用的是BHHH方法，通过公式

得到。其中，条件对数似然函数的一阶偏导数可以通过

求得。

例如，类似可以定义，sαt≡Sαt－ Sα，t－1，其中 Sαt是在样本量为 t下的关于的 α 得分函数在 k=0 时的估计。应该注意的是，sαt，sβt，sσ2t，sλt，spt与 ρ都是独立的，因为它们是 SVJ 模型的条件对数似然函数的一阶导数。假设Sk0=0，从式(11)和(14)也可以得到，

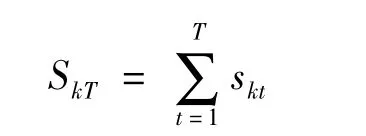
BHHH方法适合本文的问题(BHHH方法在估计Fisher信息时仅要求求一阶导数)，因为在SVJ模型的估计中关于k的对数似然函数的二阶导数是不可求的，下面证明可以构造一个独立于ρ且仅仅在写法上与LM式(12)检验不同的新的检验方法。这儿，不能计算出LM检验统计量，因为在零假设下，ρ是无法辨认的，因此得分函数式(11)和skt也是不可辨认的。现在构造一个新的检验统计量，用

下面证明 LM=sign(ρ)LM*，其中，因为，且从式(14)得 skt=

首先，从式(13)、(15)可以得到

通常，假设ρ的符号为负，因为一个负的跳跃往往引起在波动上一个正的跳跃，那么拒绝域位就会于LM*分布的负的区域。这个单边检验统计量被认为是渐进服从N(0，1)分布。但是，极限分布仍然是未知的，因此，通常用蒙特卡罗实验进行检查。

4 蒙特卡罗实验和实证分析

计算实际样本大小(n≥1 000)的检验统计量需要很长的时间，由于时间关系，本文仅进行一次小型的蒙特卡罗计算机仿真实验。样本量的大小为300，在原假设下，迭代的次数为400，在备择假设下次数为100。状态变量 θ0的初始值定为0，在原假设和备择假设下，设定参数(α，β，σ，p，λ)=(0.0，0.9，0.4，0.05，25.0)，统计量LM*的正态性可以通过J－B统计量来检验。

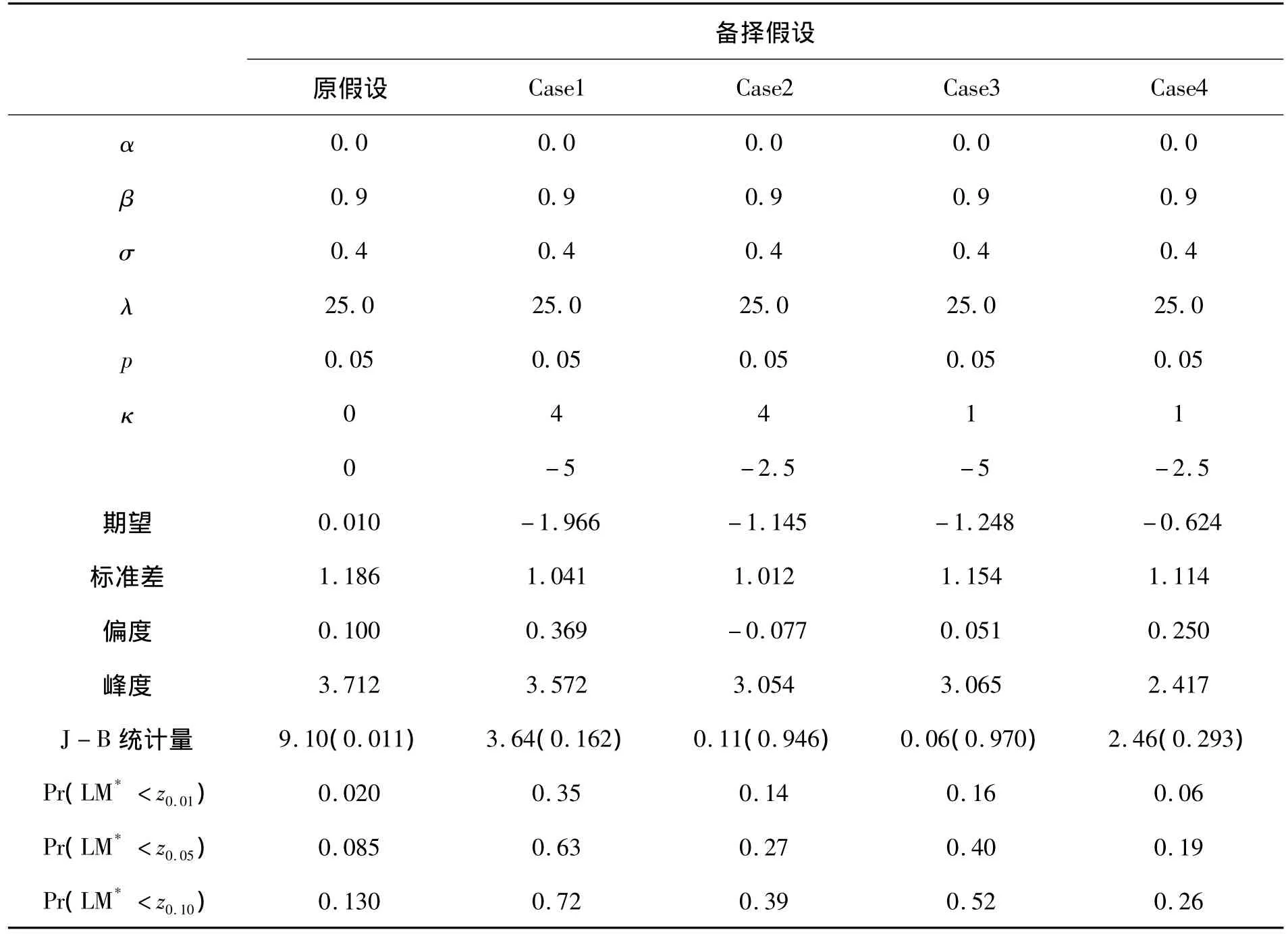
表1 在SVCJ过程中，LM*统计量在原假设和备择假设下的分布和检验能力

在原假设下，J－B统计量分布近似于χ2(2)。当显著性水平为0.05时，正态性假设被拒绝。实验结果表明，LM*检验统计量有很强的检验能力，在备择假设下，随着ρ和k程度的增加，LM*检验统计量的分布就会往负方向上偏移。

5 结束语

本文借助狄拉克·δ函数的思想，提出了在收益和波动中的跳跃项带有同期性和相关性的随机波动率过程的基础上，检验在波动方程中跳跃项存在性的拉格朗日乘子检验统计量，但它是只针对带有跳跃项的SV模型进行检验，对于其他的SV模型能否使用，是今后的研究目标。

［1］Berndt E，Hall R，Hauaman J.Estimation and inference in nonlinear structural models［J］.Ann Econ Soc Meas，1974，3:653 －665.

［2］Davies R B.Hypothesis testing when a nuisance parameter is present only under the alternative［J］.Biometrika，1977，64:247 －254.

［3］史秀红.指数自回归条件异方差模型的检验［J］.数量经济技术经济研究，2008(6):146－153.

［4］Eraker B，Johannes M，Poison N G.The impact of jumps in returns and volatility［J］.J Finance，2003，53:1269 －1300.

［5］Khalaf L，Saphores J D，Bilodeau J F.Simulation-based exact jump tests in models with conditional heteroskedasticity［J］.J Econ Dynam Control，2003，28:531 －553.

［6］Rogers A J.Modified Largrange Multiplier tests for Problems with one-sided alternative［J］.Journal of Econometrics，1986，12:112－117.

［7］Watanable T.A Non-linear Filtering Approach to Stochastic Volatility Models with an Application to Daily Stock Returns［J］.Journal of Applied Econometrics，1999，14:101 －121.

［8］Andersen T G，Hyung-Jin Chung，Bent E.fficient method of moments estimation of a stochastic volatility model:A Monte Carlo study［J］.Journal of Econometrics，1999，91:61 －87.

［9］Pan J.The jump-risk premia implicit in options:Evidence from an integrated time-series study［J］.J Finan Econ，2002，63:3 －50.