郑文治, 陈海波, 操小龙

(1. 中国科学技术大学 近代力学系 中国科学院材料力学行为与设计重点实验室,合肥 230027;2. 北京机电工程研究所,北京 100074)

拓扑优化由于其可以相当灵活地改变结构的拓扑构型,在振动与噪声控制领域受到了广泛关注。Du等[1]以辐射声功率最小为目标,对平板的材料分布进行了拓扑优化设计;之后Du等[2]将此优化框架扩展到微结构的拓扑优化设计;Zhang等[3]以目标点的声压最小为目标,基于固体各向同性材料惩罚(solid isotropic material with penalization,SIMP)模型对振动结构的阻尼材料分布进行了优化设计;吴振云等[4]使用非负声强识别结构表面对远场声辐射起主要贡献的区域,对约束阻尼板阻尼材料的最优分布进行研究。目前,大多数声振优化的研究仅考虑弱耦合,即仅考虑结构对声场的作用而忽略了声场对结构的反作用。对于像空气这种流体密度远低于结构的声学介质来说,这种简化通常是合理的,但对于像水这种重流体,则必须考虑结构和声学介质之间的相互作用,即强耦合作用。已有学者针对强耦合情况开展了研究工作。Shu等[5]基于水平集方法对声振耦合系统进行了拓扑优化设计;Chen等[6]以目标点的声压级最小为目标,对声振耦合系统中的复合材料板的微结构进行了优化。上述两项研究都基于有限元法,针对有限域的内声场问题开展的。对于无限域外声场问题,有限元法需要对较大的声场域进行离散,计算效率大大降低,且无限远处的无反射条件难以精确满足,需要进行麻烦的特殊处理[7-8]。边界元法只需在声场边界进行离散,且自动满足无限远处声场的无反射条件,对于分析外声场问题有很大的优势,因此基于有限元-边界元耦合的分析方法可以有效地用于解决外声场与结构的耦合问题[9-10]。近些年,针对外声场强耦合问题的拓扑优化的研究工作也已开展起来[11-12]。Zhao等采用有限元-边界元耦合方法,以辐射声功率级最小为目标,基于材料属性的有理近似方法(rational approximation of material properties, RAMP)模型和移动渐近优化算法(method of moving asymptotes,MMA)对声振耦合系统的材料分布进行了拓扑优化设计。

上述的拓扑优化都是在确定性的条件下进行的。然而在实际工程中,由于制造、装配、外部载荷的不可完全预测等因素,导致材料属性、几何尺寸、外部载荷等存在不确定性。传统的确定性拓扑优化忽略了系统的不确定性,可能导致优化的结果是次优的甚至完全不符合实际。因此,开展考虑不确定性的拓扑优化研究工作是很有必要的。

考虑不确定性因素的拓扑优化通常分为两种:可靠性拓扑优化[13-14]和稳健拓扑优化。可靠性拓扑优化关注的是在极端条件下系统的工作状况,而稳健拓扑优化侧重于在一定程度上减小目标函数对不确定性参数的敏感性。赵清海等[15]考虑载荷的不确定性,针对多材料结构进行了稳健拓扑优化;李冉等[16]基于随机有限元方法进行不确定性分析,考虑增材制造工艺中引起的表面层厚度不确定性进行了稳健拓扑优化;Yin等[17]基于随机摄动方法进行不确定性分析,将声介质的物理参数、外部载荷和材料特性视为随机参数,对声振耦合系统的微结构进行了稳健拓扑优化设熟计。Keshavarzzadeh等[18]基于混沌多项式展开(polynomial chaos expansion,PCE)方法量化不确定性的传播和响应的灵敏度,建立可靠性拓扑优化设计方法和稳健拓扑优化设计方法;Zhang等[19]将PCE方法拓展到声子晶体的稳健拓扑优化中;Torii等[20]使用该方法处理了考虑不确定量的发热、不确定位置的发热和不确定位置损伤的热传导稳健拓扑优化;Kang等[21]考虑材料梯度界面梯度的不确定性,基于PCE方法和水平集方法对多材料结构进行了稳健拓扑优化设计。以上研究均未涉及外声场强耦合声振系统问题,我们的文献调研也未见相关报道。

本文针对外声场与结构强耦合问题,建立了考虑材料性能空间不确定性的稳健拓扑优化模型。使用RAMP模型来描述材料分布;假设材料的弹性模量服从高斯随机场分布,通过级数最优线性估值(expansion optimal linear estimation,EOLE)方法将弹性模量随机场离散成有限个随机变量;基于PCE方法进行随机响应预测和随机响应的灵敏度分析;采用MMA算法进行设计更新,最终得到最优的材料布局。最后通过数值算例说明了考虑材料性能不确定性的必要性和本文所建立方法的有效性。

1 有限元-边界元分析方法

1.1 结构有限元分析

在简谐激励作用下,有限元离散后的结构振动方程可表示为

(K-iωC-ω2M)u=Kdu=f

(1)

式中:K,C和M分别为结构刚度矩阵、阻尼矩阵和质量矩阵;u为节点位移;f为等效节点载荷;ω为激励圆频率。

考虑声场对结构的反作用时,外载荷表示为

f=fs+fp

(2)

式中:fs为直接加载到结构的载荷;fp为声场反作用到结构上的载荷。将式(2)代入式(1)可得

Kdu=fs+fp

(3)

采用瑞利阻尼模型,结构的阻尼矩阵可以表示为刚度矩阵和质量矩阵的线性组合

C=α0M+β0K

(4)

式中,α0和β0为瑞利阻尼模型的相关系数。

1.2 声学边界元分析

在均匀理想流体介质中,声场的控制方程为Helmholtz方程

∇2p(x)+k2p(x)=0, ∀x∈Ωf

(5)

式中:p为声压;k=ω/cf为波数,ω为圆频率,cf为波速。应用格林第二公式,并将源点趋近于边界,可得常规边界积分方程(conventional boundary integral equation, CBIE)

(6)

式中:x为源点;y为场点;q(y)=∂p(y)/∂n(y)为通量,n(y)为边界点y处的外法线方向向量;系数c(x)的大小由点x处的几何性质决定,当点x处为光滑边界时,c(x)=0.5;对于三维声学问题,其基本解为

(7)

式中,r=|x-y|为源点x和场点y的距离。

同时对式(6)的两边对源点x所在边界外法向方向求导,即可得超奇异边界积分方程(hypersingular boundary integral equation, HBIE)

(8)

对外声场进行分析时,单独使用式(6)或式(8)会引起解的非唯一性问题,因此Burton等[22]提出了将两式进行线性组合,即Burton-Miller方法

CBIE+αHBIE=0

(9)

式中,α为耦合系数,本文取为-i/k[23]。对声学边界进行离散,得到式(9)的离散格式

Hp=Gq

(10)

式中:H和G为边界元系数矩阵;p和q分别为边界节点声压及其法向通量。

1.3 有限元与边界元耦合

结构与声学耦合面上需满足位移连续与力的平衡条件

q=iωρfvf=ω2ρfS-1Cfsu

(11)

fp=Csfp

(12)

式中:ρf为流体介质密度;vf为声场法向速度,Cfs和Csf为结构与流场之间的耦合矩阵;S为边界质量矩阵。

(13)

(14)

(15)

将式(11)、式(12)分别代入式(10)、式(3)中,得到声振耦合系统控制方程

(16)

通过求解上述方程,就可以完成对声振耦合系统的分析。整个系统对外辐射做功的大小可以通过辐射声功率表示

(17)

式中:W为辐射声功率; 上标()H为共轭转置; Re()为取实部。辐射声功率级可以表示为

(18)

式中,W0为参考声功率,本文取W0=2×10-12W。

2 随机场模型及随机响应分析

2.1 随机场离散

本文考虑采用高斯随机场t(x)描述材料弹性模量的不确定性,其均值为μ(x),其协方差函数为

(19)

式中: cov(x1,x2)为随机场的协方差函数;σ为随机场的标准差;l为随机场的相关长度; |x1-x2|为点x1和点x2的距离。

首先,将随机场域离散为一系列节点x1,…,xn,则随机场的协方差矩阵为

(20)

基于EOLE方法[24],随机场可以表示为

(21)

式中:Cv=[cov(x1,x),cov(x2,x),…,cov(xn,x)]T;λk,ψk分别为协方差矩阵Cm的特征值和与之对应的特征向量;ξ1,ξ2,…,ξk,…,ξn为互不相关的随机变量,其均值和方差满足

E[ξi]=0, E[ξiξj]=δij

(22)

式中: E[]为期望;δij为Kronecker delta符号。

为了减小问题的维数,将特征值λk降序排列,对式(21)取前s(s≤n)项进行截断

(23)

随机场的截断精度误差为

(24)

根据式(23)就可以实现对随机场的有限离散。

2.2 基于PCE方法的随机响应分析

对随机场离散后,得到一系列互不相关的随机变量ξ=[ξ1,ξ2,…,ξs]T, 声振耦合系统的随机响应通过PCE方法进行预估

(25)

式中:Y(ξ)为系统响应;yi为多项式的系数;φi(ξ)为多项式的正交基函数,正交于随机变量ξ的概率密度函数。对于不同的概率分布,多项式的形式会有不同,例如当随机变量ξ服从均匀分布时,φi(ξ)为Legendre多项式; 当随机变量ξ服从高斯分布时,φi(ξ)为Hermite多项式。正交基函数φi(ξ)满足

(26)

对于多维随机变量ξ=[ξ1,ξ2,…,ξs]T,多项式函数φi为

(27)

式中:καj为随机变量ξj的αj阶多项式;φi的阶数为

(28)

为了在保证计算精度的前提下,有效降低计算量,一般将式(25)截断为有限项

(29)

式中,多项式系数的项数N+1取决于随机变量的维数s和PCE的阶数m

(30)

求解混沌多项式展开的关键在于求解其中的系数yi,利用多项式φi的正交特性可得

(31)

由式(31)可得

(32)

(33)

式中:ρ(ξ)为随机变量ξ的概率密度函数;ξ(q),w(q)和nq分别为积分点、权值和积分点数目。由于本文采用的是高斯随机变量,所以采用Gauss-Hermite数值积分计算,由此可求解系数。

计算得到式(29)的系数yi后,响应Y(ξ)的均值E[Y(ξ)]和标准差σ[Y(ξ)]可以通过下式获得

(34)

(35)

3 稳健拓扑优化设计

3.1 确定性拓扑优化数学模型

拓扑优化是通过优化材料的空间分布,在满足约束的前提下最大程度的改善结构性能。声振耦合系统一般选择位移幅值、声压级、声功率级作为目标函数,其数学模型表达为

(36)

式中: 目标函数为结构位移u和声压p的实函数;ρ=[ρ1,ρ2,…,ρNe]T为设计变量;Ne为设计变量总数;ve为第e个单元的体积;fv为体积比约束。对于本文研究的声振耦合问题,除了满足上述的材料体积约束之外,还要满足式(16)的控制方程。

3.2 稳健拓扑优化数学模型

与确定性拓扑优化相比,稳健拓扑优化考虑了随机变量对结构响应的影响,其目标是寻找对随机变量不敏感的优化设计,目标函数的形式通常是随机响应的均值和其标准差的加权和,属于多目标优化设计。其数学模型表述为

(37)

式中,k为随机响应标准差的权值因子。

3.3 材料插值模型

本文通过优化双材料的分布,在满足约束的条件下达到减振降噪的效果。本文采用RAMP插值方法来描述双材料的分布并建立设计变量ρ和材料分布的关系,可以将单元矩阵表示为

(38)

(39)

式中:Ke,Me分别为第e个单元的刚度矩阵、质量矩阵;Ke1和Ke2,Me1和Me2是与分别给定的两个材料相关的刚度矩阵和质量矩阵;ρe=1为该单元完全由材料1(强材料)组成,ρe=0为该单元完全由材料2(软材料)组成;η为让中间密度趋近于0或1的惩罚因子,通常取5。

3.4 确定性条件下的灵敏度分析

确定性拓扑优化的目标函数对于设计变量ρe的导数可以表示为

(40)

(41)

式中,λ1,λ2为伴随乘子。则目标函数对于设计变量的灵敏度可以表示为

(42)

由于G,H只与频率、几何形状有关;Csf,Cfs,S只与几何现状有关;均与设计变量无关。本文考虑的载荷fs也与设计变量无关。因此,式(42)可以简化为

(43)

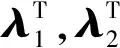
(44)

(45)

则,式(43)进一步简化为

(46)

3.5 随机响应的灵敏度分析

随机响应相对于设计变量的灵敏度也采用PCE方法进行表示

(47)

式中,系数zi可根据与式(32)类似的方法获得

(48)

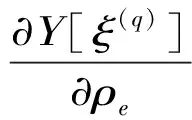
(49)

(50)

由此可得,稳健拓扑优化问题的目标函数的灵敏度为

(51)

3.6 稳健拓扑优化设计流程

基于以上随机响应的灵敏度信息,采用MMA算法进行设计变量更新。收敛条件为当两个相邻迭代步的目标函数的相对比值小于一个特定的常数τ

(52)

式中,Ji为第i步迭代对应的目标函数。本文中取τ=5.0×10-5。为了有效消除中间密度单元,使单元的相对密度趋近于0～1分布,本文采用保体积密度过滤方法[25],且将过滤半径设为0.05 m。该过滤方法中的β参数会有效影响过滤的程度,β越大,过滤越明显,但是β取值过大可能导致最终结果收敛至局部最优解。本文中,在前20个迭代步,β=0;在迭代20步之后,迭代每增加一步,β增加0.5,最大不超过100。详细的优化过程如图1所示。

图1 声振耦合系统稳健拓扑优化流程图Fig.1 Flow chart of robust topology optimization of coupled structural-acoustic systems

4 数值算例

本章中,考虑水下立方壳在点激励作用下的拓扑优化问题。立方壳边长为1 m,上表面为厚度0.02 m的四边固支板,其余各面是刚性的。在上表面中心处有幅值为1 N的简谐力作用,力的方向垂直于上表面竖直向下,如图2所示。在壳的上表面划分80×80的四节点板单元进行结构分析,对于声场部分,在壳的每一个面采用40×40的四节点常量元进行声场分析。立方壳的外部介质为水,其声速为cf=1 482 m·s-1,密度为ρf=1 000 kg·m-3,不考虑立方壳内部的耦合影响。

图2 立方壳结构Fig.2 The cubic shell

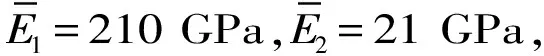
4.1 克服网格依赖性验证及体积约束影响测试

Sigmund等[26]指出采用独立于网格的过滤技术可以克服网格依赖性问题。本文采用了保体积过滤技术进行密度过滤,其过滤半径是独立于网格尺寸的。这里,我们先通过一个算例测试来说明本文的优化方法是没有网格依赖性问题的。以辐射声功率级为目标函数,材料1的体积分数约束fv=0.5;设计变量的初始值全部设置为1,即设计域全由材料1构成。分别以80×80和60×60的结构网格对在300 Hz激励下的立方壳进行拓扑优化,最终得到的拓扑优化结果如图3所示。可以看出,采用不同网格密度进行优化,最终得到的拓扑结构是基本相同的。80×80和60×60网格的最终优化结果对应的辐射声功率级分别为60.328 dB和60.340 dB, 相差很小。因此在本文中网格密度的差异不会对拓扑优化的结果产生影响。本文后续算例将采用80×80的结构网格进行计算。

图3 不同网格密度下的拓扑优化结果Fig.3 Topology optimization results under different grid densities

为了说明体积约束分数fv对优化结果的影响,这里我们以辐射声功率级为目标函数,分别在材料1的体积分数约束fv取0.5,0.6,0.7时对300 Hz激励下的立方壳进行拓扑优化。表1给出了不同体积分数约束下的优化结果对应的辐射声功率级以及优化迭代步数。可以看出随着fv的取值变大,辐射声功率级是降低的,这是因为强材料的刚度更大,强材料的应用有利于降低振动幅值,进而降低辐射声功率级。

表1 不同体积分数约束fv下拓扑优化结果对应的辐射声功率级和优化迭代步数

4.2 随机响应分析的精度验证

在介绍稳健拓扑优化之前,我们先通过一个数值算例验证本文所用的PCE方法进行随机响应分析的正确性。

我们选择4阶的PCE方法进行随机响应分析,其中计算PCE系数过程中需要计算的积分,即式(33),我们通过5阶Gauss-Hermite积分的张量积格式进行计算。表2给出了当设计域全为材料1时,即全为强材料时,采用PCE方法分别在频率为50 Hz,100 Hz,150 Hz,200 Hz,250 Hz,300 Hz,400 Hz激励下的辐射声功率级的均值和标准差的计算结果,并将其与取10 000个样本点下的蒙特卡洛方法(Monte Carlo method, MCM)得到的结果进行比较。从表2结果可以看出,在以上所述的各个频率激励下,PCE方法得到的随机响应的均值和标准差和MCM得到的结果非常相近。由此可知,采用4阶PCE方法可以获得相当精确的随机响应结果,因此在后续的稳健拓扑优化设计中使用PCE方法进行随机响应分析是可靠的。

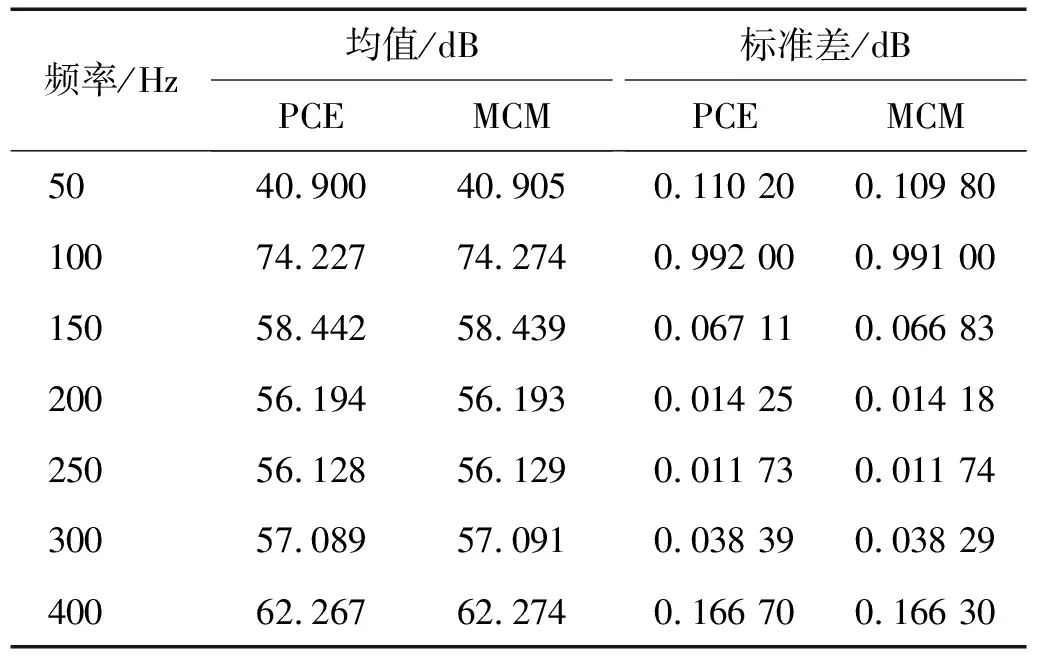
表2 PCE和MCM随机响应结果对比

4.3 稳健拓扑优化设计结果

首先对立方壳在300 Hz激励下的情况进行稳健拓扑优化设计,其目标函数取辐射功率级的均值和标准差的加权和,如式(37)所示,其中权重因子k=3;材料1的体积分数约束fv=0.5;设计变量的初始值全部设置为1,即设计域全由材料1构成。在优化44步迭代后目标函数和体积约束函数收敛。目标函数和体积约束以及辐射声功率级的均值和标准差的迭代历史如图4所示。在最初的几次迭代中,强材料的体积分数从1降至0.5,并保持在0.5附近。由于我们设计变量的初始值全部设为1,目标函数在开始时有很大的增加,但是在接下来的迭代中,目标函数、均值、标准差基本在稳定的减小,从而实现对材料分布不确定性的不敏感设计。稳健拓扑优化设计的辐射声功率级的均值为60.336 dB,标准差为0.218 0 dB。为了体现稳健优化设计的优越性,我们以辐射声功率级作为目标函数,同样基于RAMP材料插值模型和MMA算法进行了确定性拓扑优化设计。考虑材料性能的不确定性,对获得的确定性拓扑优化结果进行随机响应分析,其辐射声功率级的均值为60.351 dB,标准差为0.236 7 dB。稳健拓扑优化设计的辐射声功率级的均值和标准差均小于确定性拓扑优化结果,稳健拓扑优化结果比确定性拓扑优化具有更好的随机性能,并且对材料性能的不确定性不太敏感。稳健拓扑优化和确定性拓扑优化的结果,如图5所示。图5中,黑色表示材料1,浅灰色表示材料2,两者的结果仅有在一些细节上有所差别。

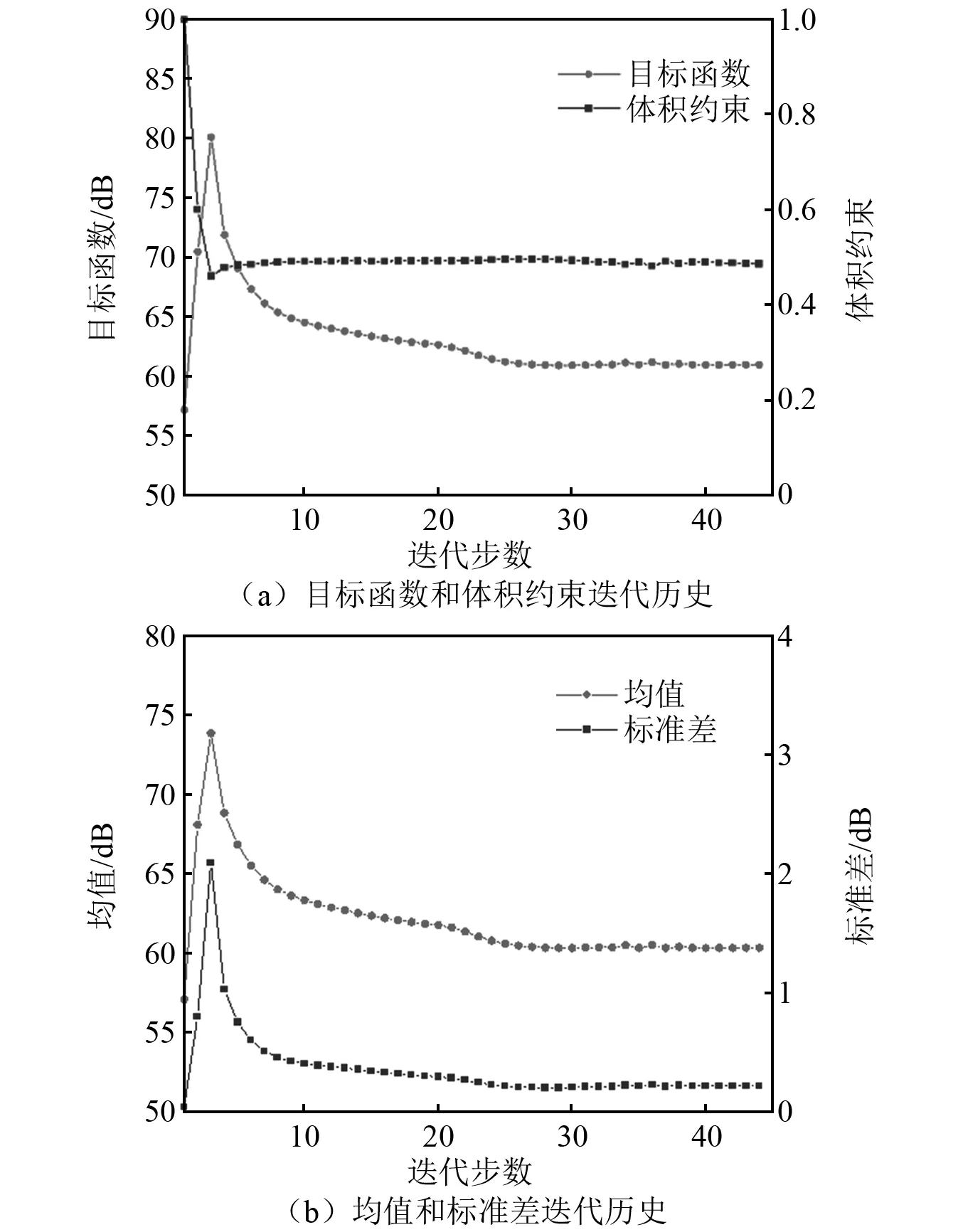
图4 300 Hz激励下稳健拓扑优化的迭代历史Fig.4 Iterative history of robust topology optimization under 300 Hz excitation

图5 300 Hz激励下的稳健优化和确定性优化结果Fig.5 Robust and deterministic optimization results under 300 Hz excitation

为了进一步研究稳健拓扑优化设计的性能,我们在与上述相同的条件和参数下又对立方壳分别在200 Hz,250 Hz,400 Hz激励下进行了稳健拓扑优化设计和确定性拓扑优化设计。图6给出了相应的确定性拓扑优化和稳健拓扑优化的结果。其中200 Hz激励下的稳健拓扑优化结果和确定性拓扑优化仅在一些细节上存在差别,但是对于250 Hz和400 Hz,稳健优化拓扑结果和确定性拓扑优化存在明显差异,这说明考虑材料弹性模量的不确定性对声振系统的拓扑优化结果有较大的影响,也说明考虑材料弹性模量的不确定性很有必要。为了更详细地比较确定性优化和稳健优化的结果,表3给出了在各个频率激励下稳健拓扑优化设计和确定性拓扑优化设计对应的辐射声功率级的均值和标准差。可以看出,与确定性拓扑优化相比,稳健拓扑优化结果的标准差都较小,这表明稳健拓扑优化设计对材料弹性模量的不确定性的敏感性更低,不仅如此,稳健拓扑优化设计的均值也都比确定性拓扑优化的均值更低。

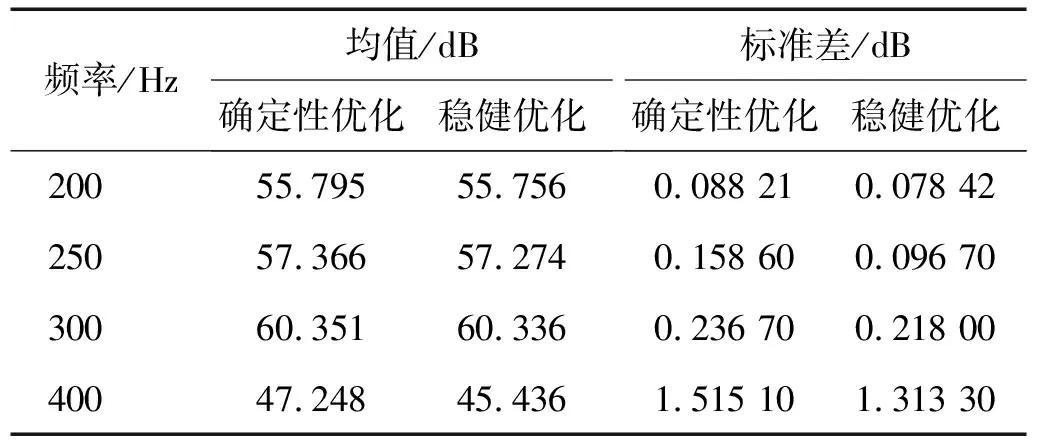
表3 确定性设计和稳健设计的辐射声功率级的均值和标准差

图6 不同激励频率下的稳健和确定性优化结果Fig.6 Robust and deterministic optimization results at different excitation frequencies

为了研究稳健拓扑优化的目标函数中的标准差的权值因子k对优化结果的影响,以5种不同的权重因子对在400 Hz激励下的水下立方壳进行稳健拓扑优化设计,其他参数设置均相同。表4中给出了采用不同权值稳健拓扑优化结果对应的辐射声功率级的均值和标准差。结果显示优化结果的辐射声功率级的均值随着权值因子k的逐渐增大而增大,标准差逐渐减小,这和双准则优化问题帕累托解的基本特征是吻合的。同时也表明随着权值因子k的增大,目标函数中标准差的权重变得更大,有利于降低优化结果对材料弹性模量的不确定性的敏感性。图7给出了k取1,2,4,5时的稳健拓扑优化结果,k取3时的结果已在图6(e)中给出。从这些稳健优化得到的结果上可以看出,不同的权值因子k得到的优化结果存在明显的差异。综上所述,权值因子k对优化结果有较大的影响,选择合适的权值因子k对于稳健优化设计至关重要。

表4 400 Hz激励下不同权值因子k下的稳健设计对应的辐射声功率级的均值和标准差

图7 400 Hz激励下不同权值因子k的稳健优化结果Fig.7 Robust optimization results of different weight factors k under 400 Hz excitation

为了研究两材料弹性模量的变异系数的影响,在其他参数保持不变的情况下,以4种不同的变异系数γ对在400 Hz激励下的立方壳进行了稳健拓扑优化设计,目标函数中的权重因子k都取3。图8给出了变异系数为0.06,0.16,0.25时对应的稳健拓扑优化结果,γ=0.10对应的优化结果已在图6(e)给出。当不确定性较小时(γ=0.06),稳健拓扑优化结果和确定性拓扑优化结果较为相近,随着变异系数的增大,稳健拓扑优化结果和确定性拓扑优化的差异也越来越大。表5中给出了变异系数γ取不同值时,稳健拓扑优化设计对应的辐射声功率级对应的均值和标准差。

表5 400 Hz激励下不同变异系数γ下的稳健设计对应的辐射声功率级的均值和标准差

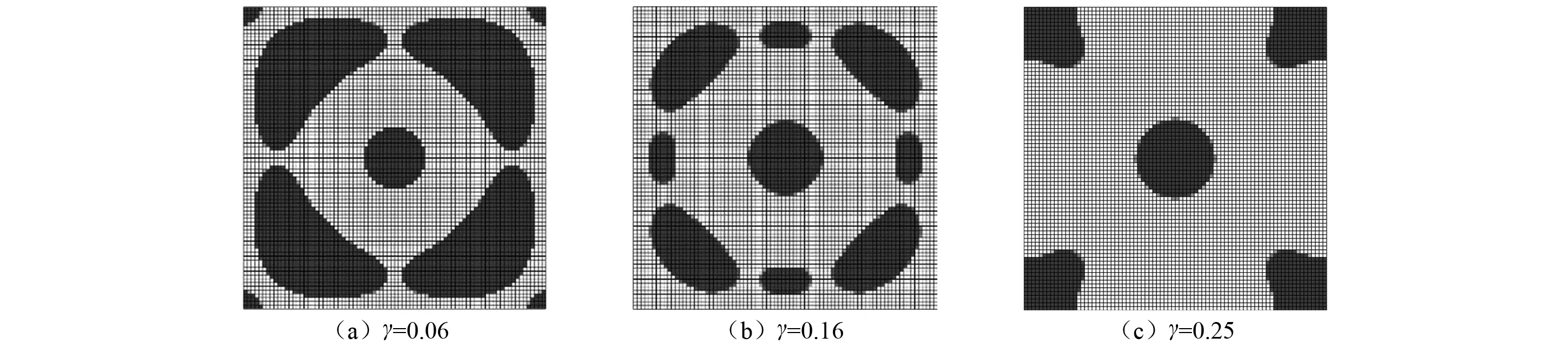
图8 400 Hz激励下不同变异系数γ下的稳健优化结果Fig.8 Robust optimization results with different coefficients of variation γ under 400 Hz excitation

5 结 论

本文研究了考虑材料性能的不确定性情况下,外声场与结构强耦合情况下的稳健拓扑优化问题。通过随机场模型描述两材料的弹性模量的不确定性,采用EOLE方法将随机场离散为有限个不相关的随机变量;采用PCE方法进行随机响应预估和随机响应的灵敏度分析;采用RAMP模型进行密度插值,建立单元相对密度和弹性模量、材料密度之间的关系;稳健拓扑优化的目标函数为辐射声功率级的均值和标准差的加权和;采用MMA算法对优化问题进行更新迭代求解。数值结果表明:

(1) 由于采用了独立于网格尺寸的过滤方法,提出的拓扑优化方法没有网格依赖性问题。

(2) 与确定性拓扑优化设计相比,稳健拓扑优化设计对应的辐射声功率级的标准差更低,实现了对材料性能不确定性更加不敏感的设计,证实了本文建立的考虑材料性能不确定性的稳健拓扑优化模型的有效性。

(3) 随着权值因子k的增大,稳健拓扑优化设计的辐射声功率级的均值逐渐增大,标准差逐渐减小,且权值因子k对稳健拓扑优化结果的影响也较大。选择合适的权值因子k很重要。