贺苏娟 邹为

(华南师范大学数学科学学院,广州 510631)

耦合Stuart-Landau 极限环系统为研究含振幅自由度的自持续振荡系统同步相变和集体动力学提供了一个重要的范式模型.本文研究了平均场反馈下全局耦合Stuart-Landau 极限环系统中3 种典型的可解集体动力学:非相干态、振幅死亡及锁频态.在热力学极限 N →∞ 情形下,利用非相干态线性稳定性分析揭示了耦合系统中同步发生的临界条件,发现了增强平均场反馈强度可使得耦合系统在更小的扩散耦合强度下出现同步相变行为;通过对振幅死亡态的线性稳定性分析得到了参数空间中振幅死亡的稳定区,发现了平均场反馈强度可有效地消除耦合系统中的振幅死亡现象;从理论上分析了锁频态的存在性条件,并从锁频态序参量的自洽关系中推导出了振幅死亡区的边界线.本文的研究揭示了平均场反馈对耦合非线性系统中集体行为的动力学控制作用,加深了平均场反馈技术对耦合诱导的集体行为影响的理解,进一步阐释了复杂耦合系统中自组织行为的涌现规律与机制.

1 引言

大量单元通过相互作用而自组织形成的集体行为在自然界中普遍存在,其动力学行为的演化规律与机制可通过耦合非线性振子模型进行定性与定量的探索[1-4].近些年来,耦合非线性振子系统中各种丰富集体动力学受到不同研究领域学者们的广泛关注[5-7].其中,同步现象是自然界中最普遍与最典型的集体行为之一,自1975 年Kuramoto模型提出以来[8],同步现象的研究已经取得了大量的理论进展;迄今,Kuramoto 模型已经成为从物理学到生物学与工程学等众多学科领域中同步行为研究的范例[9-12].Kuramoto模型是由一组全局耦合的相振子来描述的,通常可有效地刻画弱耦合系统中的同步相变行为[13-15].然而,当系统之间的耦合强度变得足够强时,为了获得对耦合系统集体动力学的完整描述,子系统的振幅自由度一般不能被简单地忽略.在强耦合非线性系统中,振幅自由度通常在决定集体行为涌现形式方面起着关键性作用,譬如鸟群、鱼群、无人机或昆虫群等[16-18].同时包含相位与振幅自由度的模型对于理解强耦合非线性系统中的分岔也具有特别重要的意义.结合相位和振幅动力学的一个最简单模型被称为Stuart-Landau 极限环系统[19],它是描述超临界霍普夫(Hopf)分岔的标准形式.在弱耦合的极限下,全局耦合Stuart-Landau 振子系统事实上可退化为经典的Kuramoto 相位模型[20].

通过考虑单个子系统的振幅动力学,许多有趣的新的集体行为在耦合非线性振子系统被发现,通常这些现象在不含振幅自由度的纯相位模型中是不存在的[21,22].其中,最为典型的一个现象是振幅死亡(amplitude death)[23,24]:指自持续振荡系统的振幅由于耦合作用而被完全抑制.从动力学角度看,振幅死亡是由于子系统间的相互耦合作用而使得均匀不动点从非稳变为稳定,进而消除耦合系统的宏观振荡的一种集体行为.过去的几十年里,耦合Stuart-Landau 极限环系统经常被用作一个理想的数学模型来探索振幅死亡现象的涌现规律,其中许多导致振幅死亡行为的不同动力学机制相续被提出,譬如频率不匹配[25-27]、时滞耦合[28-30]、动态耦合[31]、共轭耦合[32,33]、非直接耦合[34]等.除了振幅死亡现象外,全局耦合Stuart-Landau 极限环系统也可表现出其他有趣的集体行为[35-37]:非相干态(incoherence)与锁频态(locked states).在非相干态中,耦合极限环系统的宏观振荡行为消失,但每个子系统却以其固有自然频率沿着共同的极限环做周期运动.此外,在强耦合情形下,耦合Stuart-Landau 极限环系统可经历锁频态,指每个子系统被吸引到不同的不动点上.本质上,振幅死亡、非相干态和锁频态这三类集体行为是耦合Stuart-Landau 极限环系统的不同类型的定态动力学行为,其共同点是振子数目在相空间的分布并不会随时间变化.

在过去的近十年里,对同时具有相位和振幅自由度的耦合非线性系统中集体行为的理论研究如春笋般地涌现.例如,Schwab 等[38]研究了非直接耦合Stuart-Landau 极限环系统模型,并解析地推导出了非相干态、振幅死亡和锁频态3 种集体行为在参数空间中的边界线.考虑子系统振幅参数服从一定的概率分布函数,Lee 等[39]从理论上深入地研究了全局耦合Stuart-Landau 振子的宏观动力学.通过调节耦合作用方式,Wang 和Garnier[40]在全局耦合Stuart-Landau 极限环系统中建立从连续到不连续的同步相变过程;特别地,他们通过对非相干态的线性稳定性分析解析地推导出了向前相变点的临界耦合强度.令人惊讶的是,即使在全局耦合的全同Stuart-Landau 振子系统中,研究人员也发现了大量的新奇的集体行为,如奇异态[41]、广泛多稳态[42]、多集团态[43]等.最近,相位约化技术(phase reduction technique)已成功地从相模型扩展到了全局耦合的全同Stuart-Landau振子系统中[44,45],该研究具有重要的理论意义,这将更加有利于耦合Stuart-Landau 极限环系统中集体行为的深入研究.

众所周知,反馈作用在许多自然系统中普遍存在,譬如神经网络[46]、基因网络[47]、视觉系统[48]等.反馈在系统动力学控制与同步控制问题中的重要性在电子学、生物学、量子信息等各个领域已被广泛地报道.例如,脑深部刺激中反馈控制已被发现是治疗震颤(tremor)、肌张力障碍(dystonia)、帕金森病(Parkinson’s disease)等慢性神经疾病最有效的治疗方式[49-51].本文研究了平均场反馈下全局耦合Stuart-Landau 极限环系统中的集体行为.通过引入平均场反馈,研究结果表明,在热力学极限N →∞情形下,这种推广的耦合Stuart-Landau极限环系统模型中的定态集体动力学行为是可解的.具体地,首先通过对非相干态的线性稳定性分析解析地得到了系统发生同步时平均场反馈强度与扩散耦合强度所满足的具体条件,发现了平均场反馈利于耦合系统的同步行为的发生;其次通过对振幅死亡态的线性稳定性分析得到了参数空间中振幅死亡区的解析边界线,发现了平均场反馈可有效地消除耦合系统中的振幅死亡现象;最后对锁频态的存在性条件给出一定的理论刻画,并从锁频态序参量的自洽方程中进一步地推导出了振幅死亡稳定区的边界曲线的解析表达式.

本文内容安排如下:第2 节引入带平均场反馈的全局耦合Stuart-Landau 极限环系统模型,并给出了序参量的具体定义和在序参量下模型的不同表达形式;第3 节分别对模型的非相干态、振幅死亡和锁频态3 种集体行为做了系统的理论分析,包括通过对非相干态与振幅死亡态的线性稳定性分析得到了各自稳定的解析条件,并通过数值模拟结果证实了理论预测的有效性;最后,第4 节对全文内容进行概括总结,并对下一步的研究进行了展望.

2 理论模型

本文考虑平均场反馈下N个全局耦合Stuart-Landau 极限环振子的模型,其动力学演化方程如下:

其中j1,2,···,N(N ≫1),zjxj+iyj是复变量,ωj代表第j个振子的固有自然频率,K1≥0 是全局扩散耦合强度,K2≥0 刻画平均场反馈强度.当扩散耦合强度与平均场反馈强度为零,即K1K20时,单个Stuart-Landua 系统是一个超临界Hopf 分岔的范式模型[1],其有一个稳定的极限环zj(t)与一个非稳的焦点zj0.

为了定量地刻画耦合系统(1)的集体动力学特性,引入如下的复序参量:

其中R和ϕ是复序参量幅值和幅角.此时,方程(1)可改写为如下形式:

在极坐标系下,方程(4)可进一步地表达为

当平均场反馈强度K20时,方程(1)退化为文献[35,36]中所研究的模型.研究表明当逐渐增强扩散耦合强度K1时,全局耦合Stuart-Landau极限系统可表现出3 种典型的定态集体动力学行为:非相干态、振幅死亡与锁频态.耦合系统(1)中的宏观定态集体行为是统计意义上的,指相空间中振子的概率密度分布并不会随时间演化而变化,即序参量(3)中R与ϕ均为常数.本文将在热力学极限N →∞下,从理论上研究平均场反馈作用对全局耦合Stuart-Landau 系统中定态集体行为的影响.特别地,将在扩散耦合强度与平均场反馈强度的参数空间中严格地得到非相干态、振幅死亡与锁频态涌现条件的解析形式.

3 理论与数值结果

3.1 非相干态

耦合系统(1)中的非相干态是一种无序态(非同步态),每个振子都在半径为|zj|的极限环上以各自的自然频率ωj旋转,且满足序参量〈z〉0.显然非相干态存在的前提条件为扩散耦合强度满足K1＜1.特别地,平均场反馈作用K2不会影响非相干态解的存在性,但可能会改变其稳定性.严格来讲,非相干态仅在热力学极限N →∞下才存在.

当N →∞时,耦合系统(1)的宏观动力学可方便地由概率密度分布函数f(r,θ,ω,t) 来描述,其中f(r,θ,ω,t)rdθdr表示t时刻频率为ω、介于区间r ∈(r,r+dr)和θ ∈(θ,θ+dθ) 内振子的占比或振子数密度,其满足归一化条件:

由于系统的振子数量守恒,分布函数f(r,θ,ω,t) 满足如下极坐标系下的连续性方程:

在非相干态中,对每一个频率ω,振子均匀地分布在半径为ra的圆环上,故非相干态对应的概率密度分布函数为

可直接验证(10)式中非相干态的解满足连续性方程(8)及其对应的序参量R0.

令F(r,θ,ω,t)f(r,θ,ω,t)r,连续性方程(8)可改写为

相应地,序参量的幅值与非相干态的解分别为

注意,(11)式和(12)式为耦合系统(1)在热力学极限N →∞下的集体动力学提供了一个简洁的自洽描述.

为得到非相干态失稳的临界条件,接下来对其做线性稳定性分析.对(13)式中非相干态解F0引入一个小的扰动:

其中 0＜ε ≪1.将(14)式代入(12)式有

其中A,B,C,D均独立于r与θ.将(17)式中F1的形式解代入(16)式的左边,并利用δ函数等式

可分别计算出A,B,C,D的具体表达式为

利用(19)式,将F1的具体解(17)式代入(15)式后,等式两边消掉非零的R1,可得到关于s的方程:

其中g(ω) 假定是关于原点对称的偶函数.当且仅当方程(20)没有正实部根s时,非相干态是线性稳定的.特别地,在方程(20)中通过取极限s →0+,可得到非相干态稳定的临界扩散耦合强度与临界平均场反馈强度需满足

(21)式很好地从理论上预测耦合系统(1)在系统尺寸N充分大时非相干态失稳的临界条件.

为验证(21)式中理论预测的有效性,接下来通过展示方程(1)的数值模拟结果来直观地显示耦合系统中非相干态的行为规律.在数值实验中,固定N10000,利用四阶Runge-Kutta 方法与随机初始条件对方程(1)进行数值模拟,其中振子的自然频率服从(2)式给出的高斯分布.图1(a)给出了不同平均场反馈强度K2下序参量R随扩散耦合强度K1的相变图,其中频率标准差固定为Δ0.2.显然可以看到,随着K2的增大,系统非相干态失稳(R的值从零变为非零)的临界扩散耦合强度K1c逐渐减小.图1(b)进一步给出了在不同K2值下K1c随Δ的变化关系,其中实线为(21)式给出的理论预测,蓝色的方形实点为数值结果,可以清晰地看到数值模拟与理论预测一致.

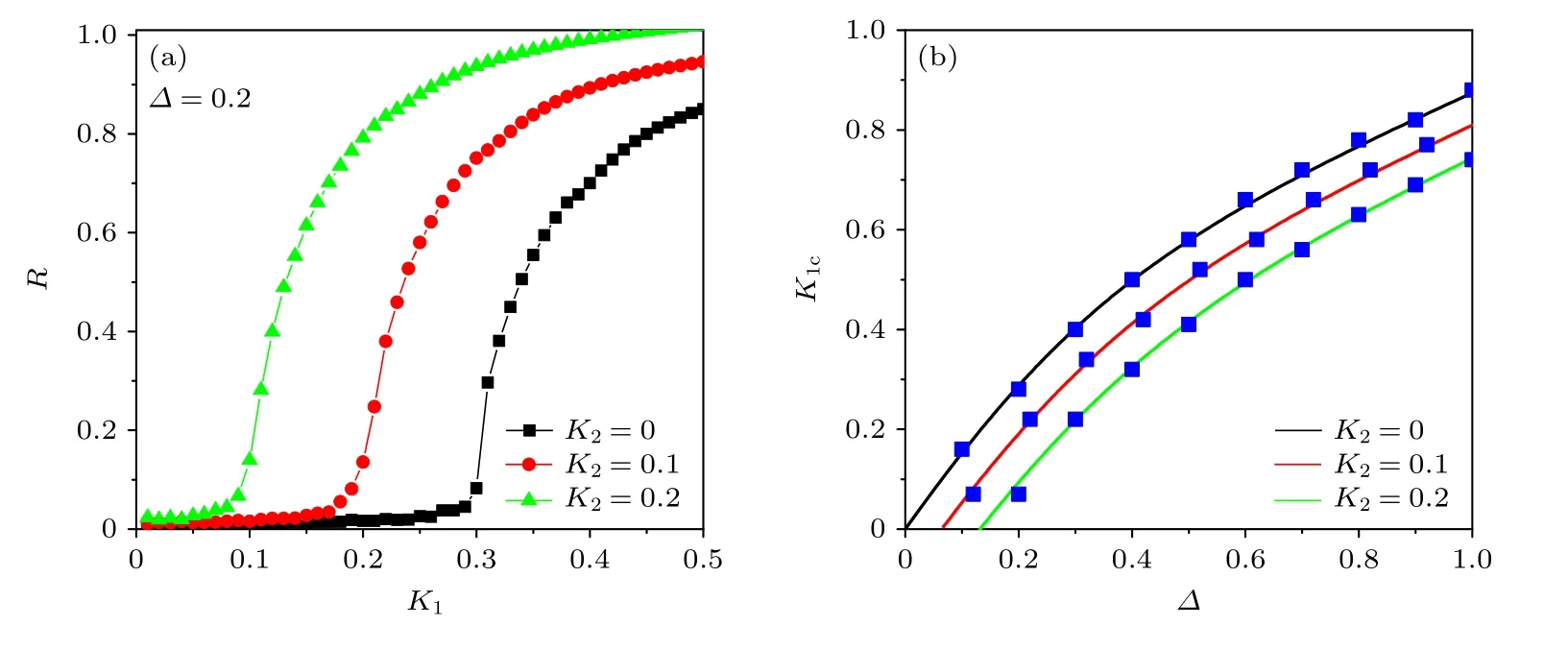
图1 平均场反馈对全局扩散耦合系统(1)中非相干态的影响(a) 不同平均场反馈强度 K2下,序参量R 随扩散耦合强度K1的相变图,其中频率标准差固定为 Δ0.2 ;(b) 不同平均场反馈强度 K2下,使得非相干态失稳的临界扩散耦合强度K1c与频率标准差Δ 的关系.实线为(21)式给出的理论预测,蓝色的方形实点为数值结果Fig.1.Effect of mean-field feedback on the incoherence in coupled system(1):(a) Phase transition diagrams of order parameter R with the strengths of diffusive coupling K1 under different strengths of the mean-field feedback K2,where the standard deviation of natural frequencies is fixed at Δ0.2 ;(b) dependence of the critical diffusive coupling strength K1c,beyond which the incoherence becomes destabilized,on the standard deviation Δ of natural frequencies under different strengths of the mean-field feedback K2.The solid lines are the plots of the theoretical prediction given in Eq.(21),whereas the blue squares denote the numerical results.

3.2 振幅死亡

当扩散耦合强度与平均场反馈强度均为零,即K1K20时,方程(1)中第j个Stuart-Landau系统在半径为|zj|1 的极限环上以频率ωj旋转,且有一个非稳的焦点zj0.显然,对于任何的K1＞0与K2＞0,zj0 依然为方程(1)的一个解.特别地,当平均场反馈强度K20时,前人研究表明在一定的固有自然频率分布与扩散耦合强度K1＞0 下[25],不动点zj0 可转变为方程(1)的一个稳定解,即耦合系统(1)经历所谓的扩散耦合诱导的振幅死亡现象[23,24].通过在耦合振子系统中引入反馈,Chandrasekar 等[52]首次研究了两个耦合的非全同Stuart-Landau 振子系统中反馈作用对振幅死亡的影响,他们发现反馈的出现可消除参数不匹配诱导的振幅死亡现象.进一步地,Zhao 和Sun[53]揭示了平均场反馈可消除两个耦合的Stuart-Landau 振子系统在不同耦合情形下的振幅死亡行为.最近,Shi 等[54]将平均场反馈扩展到更一般的形式:使用双权重反馈作用于耦合Stuart-Landau 系统中的每个振荡器.他们发现消除振幅死亡现象的反馈作用中存在一个最优的权重值.本节将从理论上揭示平均场反馈对N(N ≫2)个全局耦合非全同Stuart-Landau 振子系统中振幅死亡的作用;特别地,通过严格的线性稳定性分析,在热力学极限情形(N →∞)下得到依赖于扩散耦合强度K1与平均场反馈强度K2的振幅死亡态稳定的精确条件.

为了得到振幅死亡的发生条件,对方程(1)在解zj0 处进行线性稳定性分析.将带小扰动的振幅死亡解zj0+εηj(0＜ε ≪1) 代入到(1)式中展开,只保留ε的一阶线性项后,可得到如下的线性方程:

其中j1,2,···,N.由(22)式可知,耦合系统(1)在zj0 处线性化后的雅可比矩阵为

振幅死亡稳定的充要条件为(23)式中的矩阵M所有特征值的实部都小于零.

记aj1-K1+iωj,按照行列式的性质,矩阵M的特征方程 det(λI-M)0 可具体地计算为

故方程(1)在解zj0 处线性化后的特征方程最终为

如果特征方程(24)只有实部为负的根,则耦合系统(1)中的振幅死亡态是稳定的.反之,如果特征方程(24)有一个实部为正的根,则振幅死亡态是非稳的.

一般情况下,当N ＞2时,(24)式所给出的特征方程的根很难解析地求解,因为它们依赖于特定频率ω1,ω2,···,ωN的具体分布.然而,在热力学极限N →∞情形下,特征方程(24)的根的求解问题可得到极大的简化且易于解析地处理.具体地,当N →∞时,(24)式中左边的两部分分别对应于振幅死亡的连续谱和离散谱.一方面,振幅死亡的连续谱可直接求得为

其中 support(g) 为使得g(ω)0 的ω的集合.显然,当K1＞1时,连续谱是稳定的,即连续谱不会诱导振幅死亡失稳.另外一方面,振幅死亡的离散谱由如下方程的根给出:

若(26)式的根的实部均为负数,则离散谱是稳定的.特别地,在方程(26)中令λ →0时,可得离散谱决定的振幅死亡稳定的临界条件为

值得强调的是,热力学极限N →∞情形下,连续谱(25)式与离散谱(26)式所预测的振幅死亡稳定区具有重要的理论意义,它为具有足够大的尺寸N的耦合系统(1)中振幅死亡的涌现提供了一个相当准确的描述.

图2(a)给出了使得振幅死亡稳定的扩散耦合强度K1区间随着平均场反馈强度K2的变化,其中频率标准差固定为Δ1.5.随着K2的增大,稳定的振幅死亡区间逐渐变小,并最终彻底地消失.图2(b)进一步地给出了平均场反馈强度为K20,0.1和0.2时,耦合系统(1)在参数空间(K1,Δ) 中振幅死亡的稳定区.图2(a)与图2(b)中,实斜线为(27)式所给出的理论预测,蓝色的方形实点则表示数值实验得到的振幅死亡稳定区的边界.在数值实验中,固定系统的尺寸为N10000,自然频率服从高斯分布(2)式,且采用随机初始条件.图2表明理论分析与数值模拟的结果一致:随着平均场反馈强度的增大,振幅死亡稳定的参数区逐渐缩小.故平均场反馈可有效地消除扩散耦合系统(1)中的振幅死亡现象,从而恢复系统的宏观振荡行为.

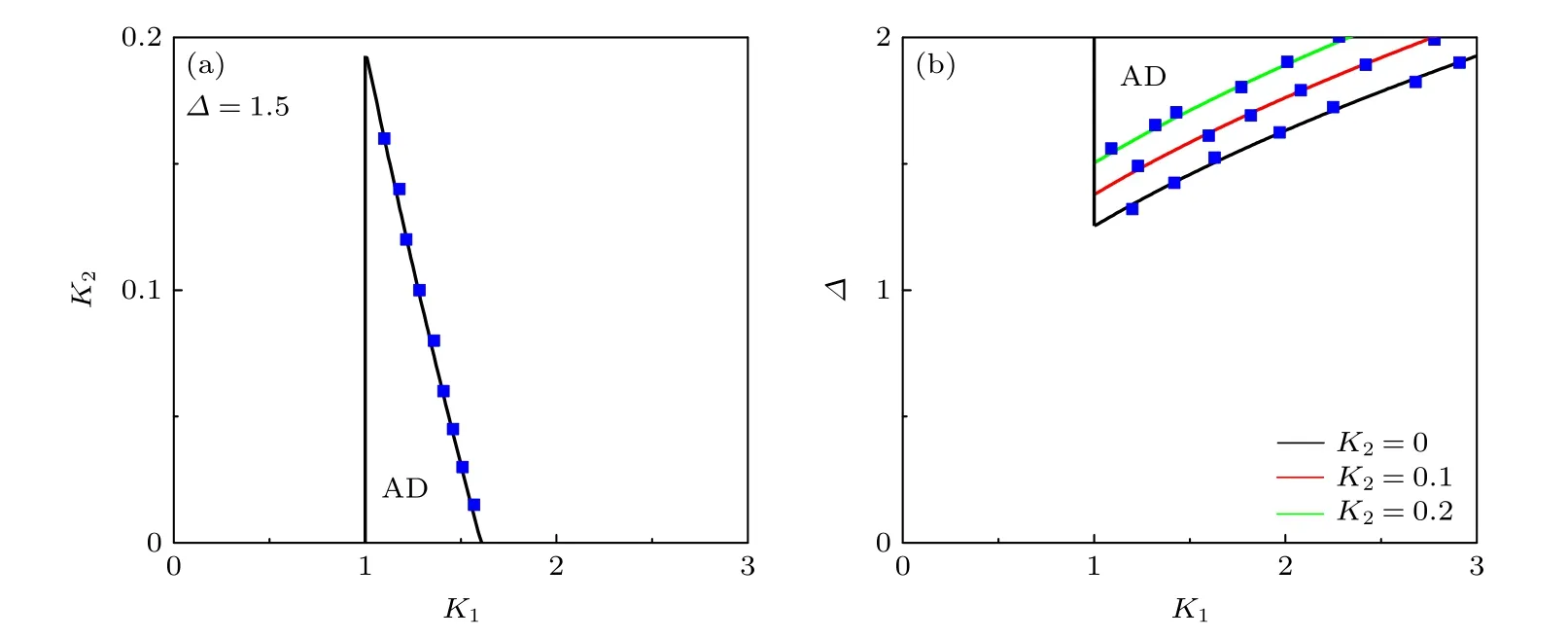
图2 平均场反馈对全局扩散耦合系统(1)中振幅死亡的影响(a) 稳定的振幅死亡扩散耦合强度 K1 区间随平均场反馈强度K2 的变化,其中频率标准差固定为 Δ1.5 ;(b) 不同平均场反馈强度 K2下,参数空间(K1,Δ) 中振幅死亡的稳定区.(a)与(b)中,蓝色的方形实点表示数值模拟结果,实斜线为(27)式中的理论预测结果Fig.2.Effect of mean-field feedback on amplitude death(AD) in coupled system(1):(a) Stable AD interval of diffusive coupling K1 versus the strength of the mean-field feedback K2,where Δ1.5 is fixed;(b) stable regions of AD in the parameter space of(K1,Δ) under different strengths of the mean-field feedback K2.In both panels,the blue squares represent the numerical results,whereas the solid lines denote the theoretical prediction by Eq.(27).

3.3 锁频态

本节讨论耦合系统(1)中的另外一种典型的定态集体行为:锁频态.注意到方程(1)具有旋转对称性,假定平均频率ω00时,锁频态对应于方程(1)的非平庸不动点解.当 2≪N ＜∞时,方程(1)的非平庸不动点解几乎不可能显式地求得.然而,在热力学极限N →∞情形下,依然可从理论上对耦合系统(1)中的锁频态获得一定程度的理解.

当N →∞时,锁频态中每个振子的位置取决于自然频率ω,故方程(1)中振子的状态变量z可看作为依赖ω的函数.由(5)式与(6)式中的极坐标方程可知,锁频态中有:

其中r,θ,R和ϕ同时满足:

(28)式—(30)式对耦合系统(1)的锁频态的解提供一个完整的自洽描述.

锁频态中,振子的位置r与θ完全由序参量R,ϕ和自然频率ω来刻画.显然,从(29)式中可得:

将其代入到(28)式有:

可进一步地写为关于 cot(θ-ϕ) 的三次方程:

它给出了锁频态中振子相位θ依赖于序参量R,ϕ和自然频率ω的一个隐式关系.此外,将(28)式与(29)式两边平方后相加,可得关于r2的一个三次方程:

它给出了锁频态中振子幅值r依赖于序参量R和自然频率ω的一个隐式关系.事实上,由(28)式与(29)式有:

可知(33)式与(34)式本质上是同一个三次方程.

注意到耦合系统(1)中的振幅死亡态其实是其锁频态的一类特殊情况,对应于方程(1)中的平庸不动点解r0,且有序参量R0.下面说明(27)式中的振幅死亡稳定区的边界线可从锁频态的序参量的自洽关系(30)式中推导出.由(31)式,方程(30)可改写为

在振幅死亡态中r0,故从(35)式可解得:

利用三角函数等式可进一步地求得:

将(38)式与(39)式代入(36)式中可得:

即为(27)式中所给出的振幅死亡稳定区的边界线表达式.

4 结论

本文在热力学极限条件N →∞下,探讨了平均场反馈下全局扩散耦合Stuart-Landau 极限环系统中的3 种典型的可解集体动力学:非相干态、振幅死亡态及锁频态.首先,通过对非相干态的线性稳定性分析,解析地得到了耦合系统发生同步的临界扩散耦合强度与临界平均场反馈强度之间满足的具体条件.理论与数值结果均表明增强平均场反馈强度可使得耦合系统在更小的临界扩散耦合强度下出现同步行为.其次,利用振幅死亡线性稳定性分析解析地得到了参数空间中振幅死亡区的临界边界线,并通过数值实验证实了理论预测的有效性.结果显示增强平均场反馈强度会导致系统的振幅死亡区逐渐缩减,进而可使耦合系统从振幅死亡态中复苏系统的集体振荡行为.最后,通过对锁频态的序参量的自洽分析得到了锁频态的一些基本理论性质;特别地,从锁频态存在性的自洽条件中进一步地推导出了振幅死亡态稳定区的边界线.

一方面,本文使用的Stuart-Landau 振子系统是描述超临界霍普夫(Hopf)分岔动力学的一个范式模型,该模型被诸多学科领域中的研究人员所广泛使用.基于Stuart-Landau 极限环模型所得的结果具有非常深刻的科学意义,常常被认为在大多数霍普夫分岔附近的非线性系统中均成立.另外一方面,反馈技术在众多的自然系统中无所不在且有着重要意义与应用,比如同步控制问题与脑深部刺激(DBS).本文是对全局扩散耦合Stuart-Landau极限环系统中集体动力学研究的一个重要拓展,本文的研究结果不仅在理论上有很好的普适意义,而且在许多物理与生物系统中都将有着重要的潜在应用.基于本文的研究未来会有更多的关于耦合非线性系统中可解集体动力学的有益探索,同时对发展平均场反馈技术的应用也有所裨益.最后,本文仅对全局耦合系统所表现出的定态集体动力学给出了相应的理论分析,缺乏对非定态的集体动力学(序参量随时间变化的振荡态,如周期、拟周期或混沌行为等)的考量以及耦合网络拓扑结构的讨论,这些重要问题未来亟需得到分析与解决.