Rozhin Yousefjani, Xingjian He(何行健), and Abolfazl Bayat

Institute of Fundamental and Frontier Sciences,University of Electronic Science and Technology of China,Chengdu 610051,China

Keywords: quantum information,quantum statistical mechanics,quantum phase transitions

1.Introduction

Quantum sensors can achieve unprecedented precision in measuring time,[1,2]electric,[3,4]magnetic,[5-7]and gravitational fields,[8,9]way beyond the capability of their classical counterparts.They can be manufactured in atomic scales and have found applications in a wide range of fields, from cosmology[10-12]to biology.[13-15]The precision of estimating an unknown parameterh, encoded in a quantum density matrixρ(h),is fundamentally bounded by Cram´er-Rao inequality aswhere Δhis the standard deviation that quantifies the accuracy of the estimation,Mis the number of repetitions andFis a positive quantity called Fisher information.The scaling of Fisher information with respect to sensing resources,such as the probe sizeL,is a figure of merit that can be used for comparing the precision of different sensors.Typically,Fisher information scales are algebraically with the size of the resource,namelyF∝Lβ.In the absence of quantum features,classical sensing at best results inβ=1,is known as the standard limit.Quantum sensors,however,can achieve superlinear scaling withβ ＞1 through exploiting quantum features such as entanglement.[16,17]Originally,enhancement in precision has been discovered for a special form of entangled states,known as GHZ states,[18]which results inβ=2 also known as Heisenberg limit.[19-27]Although there are several experimental demonstrations of GHZ-based quantum sensors,[28-32]their scalability is challenging due to the sensitivity of such delicate quantum states to decoherence.In addition,the interaction between particles in these probes is detrimental to their precision.[33-35]

Strongly correlated many-body systems are very resourceful for realizing quantum technology tasks, such as sensing.These quantum probes,which harness the interaction between particles, are naturally scalable and expected to be more robust against decoherence.In particular,various forms of phase transitions in such systems have been used for achieving quantum-enhanced sensitivity,including first-order,[36-39]second-order,[25,40-53]Floquet,[54,55]dissipative,[56-62]time crystals,[63,64]topological,[65-68]many-body[69]and Stark localization[70]phase transitions.Other types of manybody probes profit from diverse measurement methods including adaptive,[71-80]continuous,[29,62,81,84]and sequential[85,86]measurements.Since most of the sensing proposals in many-body probes have been dedicated to short-range interactions, a key open problem is whether long-range interactions can provide more benefits for sensing tasks? Longrange interactions naturally arise in certain quantum devices,such as ion traps[87-89]and Rydberg atoms.[90,91]The nature of these interactions prevents the systematic study of their interesting physics and except for some models such as Lipshin-Meshkov-Glick(LMG),[42,92]and long-range Kitaev chain,[93]the effect of long-range interaction on sensing precision remains almost untouched.

Gradient field sensing is of major importance in various fields, including biological imaging[94,95]and gravitometry.[96-99]In the former,the ultra-precise sensing of a weak gradient magnetic field increases imaging resolution,enabling the visualization of smaller tumors for early cancer detection.In the latter,precise gravity measurement is essential for detection of gravitational waves,[100,101]investigating the equivalence principle,[102]obtaining the fine-structure[103]and measuring Newton’s gravitational constant.[104]Recently,we have shown that Stark probes can be exploited for measuring weak gradient fields with super-Heisenberg precision,[70]in which the scaling exponentβcan be as large asβ～= 6.This sensor relies on Stark localization transition which could even happen in the presence of an infinitesimal gradient field in single- and multi-particle quantum systems.The effect of a longer range of interaction on this sensor has not yet been explored.Addressing this issue is essential since the physical platforms for experimental realization of Stark localization,including ion traps[87-89]and Rydberg atoms[90,91]are naturally governed by long-range interactions.

In this paper,we systematically study the effects of longrange interaction on the sensing capability of Stark probes.We show that the strong super-Heisenberg scaling of the Stark probes persists even in the presence of long-range interaction and is achievable throughout the extended phase of the system until the transition point.Our results show that various range of interaction leaves distinct imprints on the scaling of the Fisher information.Making the interaction more longranged enhances the localization and, hence, decreases the value of the Fisher information andβ.The localization effect disappears as the system gets closer to a fully connected graph and thus the sensitivity enhances again.The achievable super-Heisenberg scaling remains valid even when the state preparation time is taken into account in resource analysis.Moreover,we provide a comprehensive investigation of the critical properties of long-range Stark probes and establish a concrete relationship between critical exponents of the system through an extensive finite-size scaling analysis.We show that the enhanced sensitivity can be captured by measuring spin configurations in the relevant sector of the Hilbert space.Finally,we analyze the effect of filling factor (i.e., the number of excitations per site) on the sensing power of our Stark probes.While super-Heisenberg scaling is achievable for all studied filling factors,lower filling factors provide better precision.

This paper is organized as follows.We start by presenting the tools for assessing a quantum probe in Section 2.After introducing our long-range Stark many-body probe in Section 3,we present the numerical results of sensing with the probe in the half-filling sector in Section 4.In the subsections of Section 4,the scaling behavior of the probe,its critical properties,the resource analysis, and the optimal measurement are discussed.Section 5 contains the analysis of the filling factor and the paper is summarized in Section 6.

2.Ultimate precision limit

In this section, we briefly review the implications of Cram´er-Rao inequality for quantum sensing problems.In order to estimate an unknown parameterhencoded in a probe,described by density matrixρ(h), one has to perform a measurement which is described by a set of positive operatorvalued measure (POVM){Πi}.Each measurement outcome appears with the probabilitypi(h)=Tr[Πiρ(h)].For this classical probability distribution one can show that the classical Fisher information(CFI),defined as[16,105]

which establishes a bound on the estimation uncertainty Δh,known as Cram´er-Rao bound

whereMrepresents the number of samples.The saturation of the inequality requires an optimal estimation algorithm.For large values ofM, it is known that the optimal algorithm is the Bayesian estimator.[106,107]Note that the CFI depends on the choice of measurement.In order to have a measurement-independent quantity, as an ultimate precision limit, one can maximize the CFI with respect to all possible measurements.The corresponding quantity, known as quantum Fisher information (QFI), is thus defined asFQ(h) =max{Πi}FC(h).[108,109]Therefore,the Cram´er-Rao inequality can be written in a hierarchical form as[24,110]

This hierarchical inequality shows that the QFI can serve as a benchmark for evaluating any sensing protocol with a given measurement setup through a comparison of its corresponding CFI with the ultimate precision limit, quantified by the QFIFQ.Saturation of the ultimate precision bound, in Eq.(3),relies on both selecting the optimal measurement basis and choosing the best estimation algorithm.While the maximization with respect to measurement in the definition of the QFI seems notoriously challenging, alternative methods can provide computational-friendly methods for calculating the QFI.In particular, it turns out that the QFI is related to a quantity called fidelity susceptibilityχ(h)asFQ=4χ(h).The fidelity susceptibility is defined as[41,48,51,111]

withδhbeing an infinitesimal variation inh.It has been shown that for systems that go through a second-order quantum phase transition, the fidelity susceptibility and, hence,QFI show non-analytic behavior in the vicinity of the critical point.[48,111-114]This reflects the tremendous sensitivity of the system with respect to the control parameterhwhich drives the system into the phase transition.In this paper,we rely on Eq.(4) for calculating the QFI and investigating the sensing power of a Stark many-body probe with long-range interaction.

3.Stark many-body probe

We consider a one-dimensional spin-1/2 chain ofLsites that is affected by a gradient fieldh.While spin tunneling is restricted to nearest-neighbor sites,the interaction between particles is taken to be long-range which algebraically decays by exponentη ＞0.The Hamiltonian reads

whereJis the exchange coupling,are Pauli operators acting on sitei, andhis the amplitude of the applied gradient field, which has to be estimated.By varying the powerlaw exponentη,one can smoothly interpolate between a fully connected graph(η=0)and a standard nearest-neighbor onedimensional chain (η →∞).Inherently, many interactions are long-range.Coulomb and dipole-dipole interactions are notable examples of this interaction that can be modeled in certain quantum simulators,e.g.,ion traps[87-89]and Rydberg atoms.[90,91]The Hamiltonian Eq.(5) conserves the number of excitations in thezdirection, namely [H,Sz] = 0, whereThis implies that the Hamiltonian is blockdiagonal with respect to the number of excitationsN.Hence,each block can be described by a filling factor ofn=N/L.Here, we focus on the sensing power of our probe assuming that the filling factornis fixed and the probe is prepared in the lowest energy eigenstate of the relevant sector.Note that the true ground state of the Hamiltonian lies in the sector withn=0(i.e.,N=0 excitations).Nonetheless,throughout the paper,for the sake of convenience,we call the lowest eigenstate of the Hamiltonian for any given filling factornthe ground state which should not be mistaken by the true ground state of the Hamiltonian at filling factorn=0.

Regardless of the range of interaction, by increasing the strength of the fieldh, the probe undergoes a quantum phase transition from an extended phase to a many-body localized one.[115-119]It is known that the many-body localization(MBL) transition occurs across the entire spectrum, in contrast to the conventional quantum phase transition which occurs only at the ground state.[51]Detecting and characterizing the MBL transition across the whole spectrum usually rely on exact diagonalization which severely restricts the numerical simulations to small systems.[120]For analyzing the sensing power of a probe,one requires large system size behavior which is not accessible through exact diagonalization.Therefore,we exploit matrix product state(MPS)simulation[121]to capture the behavior of QFI in large system sizes.While this allows us to extract a precise scaling analysis, it comes with the price that we will be limited to the ground state in each filling factor and cannot analyze the sensing power of excited states.

4.Sensing at half-filling sector(n=1/2)

We first focus on the half-filling sector of the Hamiltonian in which we haveN=L/2 excitations.In Fig.1(a), we plotFQas a function of Stark fieldh/Jfor a probe of sizeL=30 with various choices ofη.Several interesting features can be observed.First, by increasingh/Jthe QFI shows a dramatic change in its behavior from being almost constant in the extended phase to a decreasing function in the localized regime.During this transition, the QFI peaks at somehmax(η),which asymptotically converge to the transition pointhcin the thermodynamic limit.[111,114]Second,variousηleave distinct imprints on the QFI.By moving from a fully connected probe(η=0)to a nearest-neighbor one(η →∞), the peaks of the QFI first decrease and then show a revival behavior.This is because asηdecreases (i.e., interaction becomes more long-range) each spin configuration induces a different Zeeman energy splitting at any given site.This effect is like random disorder potential, which helps the system to localize and thus reduces the QFI.The observed behavior continues until the system becomes close to a fully connected graph(forη～0.1) in which all spin configurations induce almost the same energy splitting and thus the localization effect from off-resonant energy separations gradually disappears.Third,strong long-range interaction indeed enhances the sensitivity of the probe by providing the highest value ofFQin both the extended phase(i.e.,h ＜hmax)and at the transition point(i.e.,h=hmax).

To explore the behavior of the QFI in the thermodynamic limit,namely forL →∞,one can study the QFI for various system sizes.In Figs.1(b)-1(d),we plot the ground state QFI as a function of Stark fieldh/Jfor various system sizesLand selectedη=0,1,and 5,respectively.Regardless of the range of the interaction,by enlarging the probe size,the peak of the QFI increases andhmaxgradually approaches zero, signaling the divergence ofFQin the thermodynamic limit for a vanishing transition pointhc→0.While the finite-size effect can be seen in the extended phase,in the localized regime one deals with a size-independent algebraic decay of the QFI which can be perfectly described byFQ∝|h-hmax|-α(η)(dashed lines).From Figs.1(b)-1(d),one can see that the exponentαtakes the valuesα(η=0)=4.00,α(η=1)=4.94,andα(η=5)=3.97,respectively.

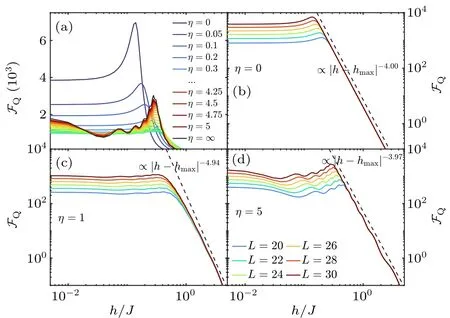
Fig.1.(a)The QFI versus Stark field h/J when our probe of size L=30 is prepared in the ground state of H(h)with n=1/2 and different powerlaw exponents η.(b)-(d)FQ as a function of h/J for probes of different sizes L initialized in the ground state of H(h) for η =0, 1, and 5, respectively.The dashed lines in all panels are the best fit of FQ, namely FQ∝|h-hmax|-α, representing the size-independent algebraic behavior of the QFI in the localized phase.

4.1.Super-Heisenberg sensitivity

Fig.2.Upper panels: the maximum of QFI(markers)versus probe size L for some values of η in(a)transition point(h=hmax)and(b)extended regime (h/J=10-4).The lines are the best fitting function of the form FQ ∝Lβ(h,η).Lower panels: the scaling exponent β(h,η)versus η obtained(c)at the transition point and(d)in the extended phase.

To characterize the scaling of the QFI with the probe size, in Figs.2(a) and 2(b), we plotFQversusLfor some values ofηboth at the transition point, i.e.,h=hmax, and in the extended phase, i.e.,h/J= 10-4, respectively.In both panels, the markers represent the QFI obtained by numerical simulation and the lines are the best fitting function of the formFQ(h,η)∝Lβ(h,η).The best obtained exponentβ(h,η)has been plotted as a function ofηin Figs.2(c)and 2(d),forh=hmaxandh/J=10-4, respectively.Some interesting observations can be highlighted.First,regardless of the interaction rangeη, one can obtain super-Heisenberg sensitivity for our probe (i.e.,β ＞2) both at the transition point and in the extended regime.Second, as discussed before, by decreasingη(i.e., making interaction more long-range)the effective Zeeman energy splitting enhances the localization and thus reduces the QFI as well as the exponentβ.Asηfurther decreases,the probe becomes effectively fully connected,implying that all spin configurations induce equal energy splitting that does not contribute to the localization anymore.Therefore,βchanges its behavior and starts rising asηdecreases towards zero.

4.2.Finite-size scaling analysis

The observed trend of the QFI in Figs.1(b)-1(d)(shown with dashed lines)strongly implies the algebraic divergence of the QFI in the thermodynamic limit asFQ∝|h-hmax|-α.For the sake of the abbreviation, we drop the dependency of the parameters onηandh.This behavior which is attributed to all second-order phase transitions in the thermodynamic limit is accompanied by the emergence of a diverging length scale asξ～|h-hc|-ν,withνknown as the critical exponent.To extract the parametersαandνin finite-size systems one needs to establish finite-size scaling analysis.In this technical method,the QFI is rescaled as

whereg(·) is an arbitrary function.Plotting the rescaled QFI, namelyL-α/νFQ, versusL1/ν(h-hc) collapses all the curves of different probe sizes and the best data collapse can be obtained for accurate selection of critical properties, i.e.,(hc,α,ν).Figures 3(a) and 3(b) illustrate the best-achieved data collapse for probes of sizeL= 20,...,30 for selectedη=0 andη=1,respectively.The critical properties for both panels, obtained using Python package PYFSSA,[122,123]are(hc,α,ν)=(1.04×10-5,4.00,1.01)and(hc,α,ν)=(0.70×10-5,4.94,1.39).For the sake of completeness,in Table 1 we report the exponentsαandνfor different values ofη.

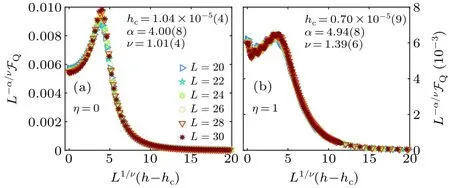
Fig.3.Finite-size scaling analysis of the QFI following the ansatz Eq.(6)in (a) a fully connected probe η =0 and (b) a probe with η =1.The optimal data collapses are obtained for the attached critical properties(hc,α,ν)in each panel.

Table 1.Extracted critical exponents including α, ν, their ratio α/ν, and the exponent β for various values of η.Here, reported α and ν that control the speed of algebraic divergence of the QFI FQ ∝|h-hmax|-α and the length scale ξ ～|h-hc|-ν in the thermodynamic limit,respectively,are obtained through finite-size scaling analysis.As it is evident from the values in the table,α/ν and β are very close to each other,which guarantees the validation of Eq.(8)for all ranges of interaction.Small deviations between α/ν and β are due to finite-size effects.

Since in the finite-size systems, the peaks of the QFI athmaxare cutoff by the system size,one hasFQ∝Lβ.The two expected behaviors of the QFI,namelyFQ∝|h-hc|-αin the thermodynamic limit andFQ(hmax)∝Lβfor finite systems at the transition point,suggest a unified ansatz for the QFI as

whereAis a constant.One can indeed retrieve the two behaviors from the above ansatz by either choosingL →∞orh=hmax.Note that, the two ansatzes of Eqs.(6) and (7) describe the same quantity and thus have to match with each other.A simple factorization ofL-βfrom the denominator of Eq.(7) shows that the two ansatzes are the same provided that the exponents satisfy

The validity of the above equation for all the consideredηis evidenced in the presented data in Table 1, in whichα/νobtained from finite-size scaling analysis of Eq.(6), matches closely withβ,obtained from scaling analysis in Fig.2(a).

4.3.Resource analysis

Up to now, we have shown that quantum criticality can indeed offer significant advantages for quantum sensing.Nevertheless, this advantage is usually hindered by the time required to prepare the ground state close to the critical points.Initializing a probe in its ground state via, for instance, adiabatic evolution,[43]demands a time that scales with the probe size ast∝Lz,[53]in which the exponentzis known as dynamical exponent and determines the rate of the energy gap closing,namely ΔE∝L-z, for a system approaching to its criticality.Taking initialization time into consideration offers the normalized QFI, i.e.,FQ/tas a new figure of merit.[42,53,86]SinceFQ(hmax)∝Lβone can easily show that the normalized QFI scales as

In order to estimate the dynamical exponentz,one has to numerically compute the energy gap ΔEversus the system sizeL.In Fig.4(a),we plot energy gap ΔEobtained through exact diagonalization as a function ofLfor a fully connected probe(η=0)in the extended phase(i.e., 0.0001 ≤h≤0.1),at the transition point(i.e.,h=hmax)and in the localized phase(i.e.,h/J=1).An algebraic decay as a function ofLfor energy gap is observed in the extended phase withz=0.91,at the transition point withz=1.04,and in the localized phase withz=0.In Fig.4(b), we plot the dynamical exponentzas a function ofηfor a probe in the extended phase (h/J=10-4) and at the transition point(h=hmax).As the results show,the exponentzqualitatively behaves similarly to the exponentβas the interaction rangeηvaries.It is worth emphasizing that even by considering time into the resource analysis, the exponentβ-zremains larger than 2 in all interaction ranges.This super-Heisenberg scaling can indeed provide a significant advantage for weak-field sensing.

4.4.Optimal measurement

Recovering the precision enhancement offered by the QFI, generally, demand performing complex measurements that may dependent on the unknown parameter.This makes it crucial to provide a suboptimal yet local and experimentally achievable set of measurements that capture the precision enhancement.Remarkably,in our probe measuring spin configurations described by observable ∑Li=1σziin the sectorSz=0 closely saturates the Cram´er-Rao inequality Eq.(3).To show this,in Fig.5 we plot both CFI(markers)and QFI(lines)captured by Eqs.(1) and (4), respectively.The curves show the sensitivity of the probe as a function of the Stark fieldhfor a system of sizeL=20 which is prepared in the ground state ofH(h)withη ∈{0,0.1,1,2}.Clearly,regardless of the interaction range, the CFI and QFI closely match showing that spin configuration is indeed an optimal measurement.The maximum of CFI happens exactly at the transition point, namelyhmax,and this quantity resembles the behavior of QFI with respect toη.

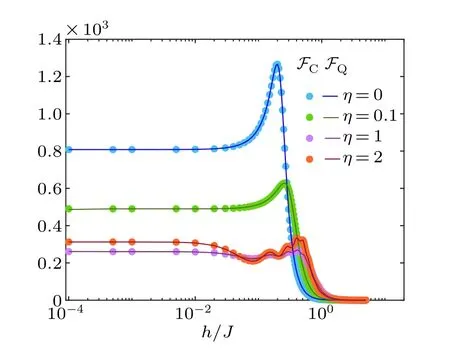
Fig.5.The QFI(filled lines)and the CFI(markers)versus Stark filed h/J for a probe of size L=20 prepared in the ground state of Hamiltonian Eq.(5)with different η.

5.Filling factor analysis

Having described the many-body Stark probe in a halffilling sector of the Hilbert space, we now focus on the effect of the filling factornon the performance of our sensor.In Figs.6(a) and 6(b), we plot the QFI at the transition pointh=hmaxas a function ofηfor filling factorsn=1/4 andn= 1/8, respectively.Clearly, analogs to the scenario ofn=1/2 (see Fig.1(a)) asηdecreases (the interaction becomes more long-range)the QFI goes down and then revives as the effective localization impact disappears.Interestingly,for larger filling factors(e.g.,n=1/2 and somehown=1/4),a fully connected probe withη= 0 outperforms the other choices ofη.As the filling factor reduces, the best performance belongs to the nearest-neighbor probe withη →∞.In addition,our results evidence that decreasingncan remarkably boost the achievable QFI.This can be observed in Fig.6(c)which representsFQ(hmax)in a probe of sizeL=32 prepared in various sectors ofn=1/2,1/4 and 1/8.These results are in line with our previous results in which the highest advance was obtained for a Stark probe with single excitation.[70]

To characterize the impact of the filling factor on the scaling of the QFI with respect toL,similar to the scenario of then=1/2,we fit the obtained QFI for different probe sizeLwith functionFQ∝Lβ(h,η).The best fits result in reportedβas a function ofηin Figs.7(a)and 7(b)forn=1/4 andn=1/8,respectively.In each panel, we report the obtainedβat the transition point (h=hmax) as well as in the extended phase(h/J=10-4).As the Figs.7(a) and 7(b) show, the exponentβshows qualitatively similar behavior to the half-filling case as the interaction becomes more long-ranged.Importantly,for all interaction ranges the exponentβshows super-Heisenberg scaling, and the best performance is always obtained for a nearest-neighbor probe.By decreasing the filling factorn,the performance of the probe in the extended phase gets closer to the one at the transition point.This is in full agreement with our previous results obtained for the Stark probe with single particle[70]in which for the nearest-neighbor probe both cases yield the sameβ.

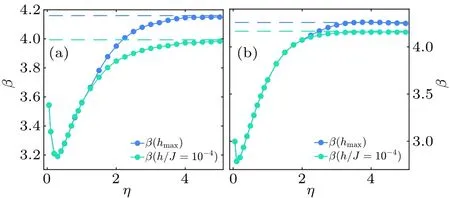
Fig.7.The scaling of the QFI, namely FQ(h,η)∝Lβ(h,η), as a function of η for (a) n=1/4 and (b) n=1/8.In both panels the extracted β is reported for the transition point h=hmax and the extended phase h/J=10-4.

6.Conclusion

Stark localization transition in many-body systems, as a result of applying a gradient field in the lattice,has been harnessed to generate an ultra-precise sensor for measuring weak gradient fields.In this paper, we address the effect of longrange interactions on the capability of these probes.Our study shows that strong super-Heisenberg precision of the Stark probe can be obtained in all ranges of interaction in the extended phase until the transition point.However,as the interaction becomes more long-range two different behaviors can be observed.Initially,by making the system more long-ranged the sensing power, quantified by QFI and its exponentβ, decreases.Then, aroundη～0.1, where the system becomes effectively a fully connected graph, the sensitivity enhances again which can be seen in the rise of both QFI andβ.These different trends can be explained through long-range interaction induced localization.In long-range interacting systems,keeping the filling factor fixed,every given spin configuration induces a different Zeeman energy splitting at each site.This energy splitting behaves like an effective random disorder that enhances localization and decreases the sensing power.When the interaction becomes almost fully connected, the energy splitting of all spin configurations becomes equal and effective localization disappears,which boosts the sensitivity of the probe.Interestingly, even by incorporating state preparation time in our resource analysis, the super-Heisenberg scaling still remains valid.In the localized phase,the system becomes size-independent and QFI follows a universal function.Several critical exponents governing the localization transition as well as their relationship have been extracted through extensive finite-size scaling analysis.Finally, we have shown that the sensitivity decreases by increasing the filling factor.

Acknowledgments

Project supported by the National Key R&D Program of China (Grant No.2018YFA0306703), the National Science Foundation of China (Grant Nos.12050410253, 92065115,and 12274059), and the Ministry of Science and Technology of China (Grant No.QNJ2021167001L).Rozhin Yousefjani thanks the National Science Foundation of China for the International Young Scientists Fund(Grant No.12250410242).