陆佳州，戴辽轩，张国胜，胡银龙，石尚，2

（1. 河海大学能源与电气学院，南京 211100；2. 东南大学自动化学院，南京 234299）

0 引言

由于具有高效率、小尺寸、高稳定性等优点，DC-DC 变换器已广泛应用于直流电机驱动、计算机系统、通信设备和其他工业系统［1-2］。DC-DC 变换器作为基础单元电路广泛应用于各类电力电子设备，其稳定性对电力电子设备在一些高科技行业的应用起着至关重要的作用，其中DC-DC 降压变换器是最重要的开关变换器之一。随着新应用的不断发展，DC-DC 降压变换器对动态响应速度和稳定性精度的要求越来越高。因此，以实现DC-DC 降压变换器输出电压精确调节为目标，选择最优的控制方法显得尤其重要。

线性平均数学模型常被用于DC-DC 变换器的控制设计问题，因此PID 控制被广泛运用［3-4］，但是PID 控制器无法消除由不确定性和外部扰动等构成的集总干扰的影响。因此，非线性控制策略给带有集总干扰的DC-DC 降压变换器带来了新的解决思路。针对这一主题，相关研究者已经提出了许多新颖控制方法，如基于观测器的控制［5］、自适应控制［6］和鲁棒控制［7］等。近年来，滑模控制（sliding mode control，SMC）因具有鲁棒性好和物理实现简单等优点，被广泛用于降压控制，并产生大量积极成果［8-9］。文献［9］介绍了DC-DC 降压变换器滑模控制器的一般设计思路。随后，在文献［10］中，研究者提出了一种通过选择滑模系数来进行有效控制的简单方法，以确保所设计的控制器也是最优的。应该注意的是，上述的所有SMC 控制器可能会遇到两个问题：一个问题是滑模变量的相对阶必须等于1，这大大限制了滑模面的选取；而第二个问题是由不连续项引起的抖振问题，这限制了它的实际应用范围。二阶滑模（second order slide mode，SOSM）技术已被广泛用于解决这两个问题［11］。作为最简单的SOSM 算法之一，文献［12］提出的twisting 控制器只需要状态变量的符号进行反馈，其中仿真结果表明，这种SOSM 控制方法可以显著减少抖振问题。在文献［13］中，针对DC-DC 降压变换器，提出了次优SOSM 控制器。文献［14］中，学者通过几何方法为DC-DC 降压变换电路提出了SOSM控制器。

以上许多控制方法都属于有限时间控制，系统收敛时间受到初始条件的严重制约，并且当初始条件趋于无穷大时将无限增长［15］。为了解决这个限制条件，固定时间收敛现象在文献［16］中首次发现并在之后得到不断发展［17-18］。近年来，固定时间控制在DC-DC 变换器中的应用也逐渐得到学者们的关注，但与有限时间控制相比，相关成果还不是很多。在文献［19］中，作者针对参数已知和未知两种情况下的DC-DC 升压-降压和降压变换器电路提出了固定时间控制算法。在文献［20］中，作者针对存在参数不确定、输入电压波动以及负载变化等未知动态的降压型变换器系统提出一种基于未知系统动态估计器的快速固定时间控制方法。然而，文献［19-20］均未考虑外部干扰对系统的影响，且当系统具有未知参数时，收敛误差只能到原点的邻域内。在最近的文献［21］中，研究者引入干扰和参数误差，针对降压电路系统设计了基于固定非奇异终端滑模控制的电压调解算法。可以发现，文献［21］中的算法也仅能让系统收敛在原点的邻域内，但是必须保证干扰具有一个已知的常数上界。然而在实际的降压电路中系统的集总干扰包含了未建模动态、内部外部扰动等，是依赖于与系统的状态的，其上界也将随状态的变化而变化。因此，常数上界假设仅能在局部条件下成立，将常数上界假设推广至函数上界更为合理。目前扰动由函数条件限定下降压电路的固定时间输出调节问题尚未解决。

基于以上分析，本文针对扰动由函数条件限定下的DC-DC 降压电路系统，设计了一种新型变增益SOSM 控制的输出电压调节算法。本文的优势主要有两个方面。

1） DC-DC 降压电路的传统控制方法许多都是误差有限时间收敛，收敛时间受初始条件影响［12-14］。不同于其他算法，本文所提出的方法可以实现固定时间收敛，收敛时间不依赖于系统初始条件，因此具有更广泛的应用。

2） 现有DC-DC 降压电路的固定时间控制［19-21］仅能保证输出误差在固定时间内收敛到原点的邻域，且所考虑的干扰具有一个已知的常数上界。本文首次在将常数上界推广至函数上界的前提下，设计变增益SOSM 算法，确保输出误差能在固定时间内精确收敛到0。

1 系统建模与预备知识

1.1 DC-DC降压变换器建模

如图1 所示为DC-DC 降压变换器系统原理图。其中Vin为输入电压源，S 为半导体开关，D 为二极管，C和L分别为滤波电容和电感，R为负载电阻。

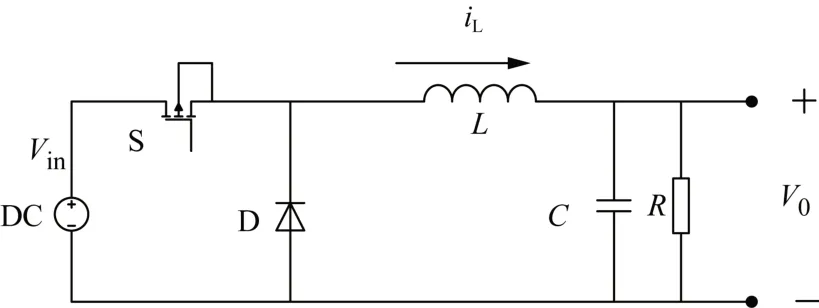
图1 DC-DC 降压变换器系统原理图Fig.1 Schematic diagram of DC-DC buck converter system

DC-DC 降压变换器可以用平均状态空间方程表示为：

式中：V0为负载电阻R的输出电压；Vin为输入电压；iL为电感L的电流；μ为PWM 的控制信号；C为电容值。但在实际情况下，变换器的参数存在一定误差，存在不确定性。此外，外部干扰也会对模型产生影响。本文以电感参数不确定和外部干扰为误差，因此将状态空间方程改写为：

式中：ΔL为L误差值；d(t)为有界干扰。

本文的设计目标是提出一种电压调节控制器，能够在参数不确定和外部干扰的情况下，让DCDC 降压变换器的输出电压V0在不依赖于系统初值的固定时间内精确跟踪期望参考电压Vref。

1.2 不等式引理

本节会介绍3 个不等式引理，为下文具体设计步骤提供理论依据。首先，做出定义：xα=|x|αsign(x)，∀x，α∈R。

引理1［22］，不等式（3）成立。

式中：x、y为实数变量；p1和p2为常数，p1＞0 且0 ＜p2＜1。

引理2［23］不等式（4）成立。

式中：x、y∈R 为实数变量；c、d＞0 是正常数；那么对任意给定函数γ＞0且∀x、y∈R。

引理3［24］不等式（5）成立。

式中：∀xi∈R，i= 1，…，n为实数变量，那么对任意实数p满足0 ＜p＜1。

1.3 固定时间稳定性

考虑如下等式：

式中：x∈Rnx为状态向量；ẋ(t)为状态向量的导数；f：R+× Rnx→Rnx为非线性函数，且可以是不连续的。当f(t，x)不连续时，等式（6）的解被称为Filippov意义下的解［25］。

定义1［15］对于∀x0∈Rnx，存在一个固定时间Tmax，且不受系统初值x(t，x0)依赖，使得等式（（6）的解收敛到0 的时间始终在Tmax内，即x(t，x0) = 0，∀t≥Tmax，那么称系统（6）在原点是全局固定时间稳定的。

引理4［26］考虑等式（6），如果对∀x0∈Rnx，存在一个全局径向无界且正定的C1函数V(x)，标量α，β＞0， 0 ＜p＜1，q＞1， 使 得V̇(x)≤-αVp(x)-βVq(x)。由此可知，等式（6）能够在原点处达到稳定，属于全局固定时间稳定，收敛时间T(x0)满足：

2 SOSM控制器设计

文献［11］阐述了SOSM 的基础理论，可知设计SOSM 控制器首先要确定一个滑模变量。定义滑模变量s1=V0-Vref，其中Vref为期望输出电压。根据文献［11］可得：

式中：滑模变量s2为s1的导数；ṡ2为s2的导数；u为控制器；a和b为平滑函数，可以表示为：

由文献［11］可知，传统的二阶滑模控制往往假设不确定项a具有已知的常数上界。由式（8）可知，a受到iL、V0限制，上界也会受iL、V0的改变而变化。因此，常数上界只能在局部状态空间内满足，从全局的角度来看这一假设非常严格。因此，本文将采用如下假设。

假设1 存在一个常数-b≥0 和函数(t，x) ≥0，使得a，b满足b≥，|a|≤(t，x)。

假设1 放宽了传统SOSM 控制中对于不确定函数a的上界要求，将a的常数上界aˉ推广至时变函数上界(t，x)。同时，假设1移除了对不确定函数b的上界要求。

2.1 主要结论

在给出主要结论之前，先选定任意参数满足ρ≥a1≥r1＞0，并定义r2=r1+τ，r3=r2+τ，其中τ∈[-，0)。

定理1 以假设1 的成立为前提，全局固定时间控制器根据式（10）进行设计。

式中：s1、s2为式（7）给出的滑模变量；(t，x)和由假设1 给出；、β1(s1)为控制器设计的变量函数。

函数、β1(s1)满足：

式中：α0＞0，β0＞0 为任意给定正常数；c1(β0)、c2(s1)、c3(s1)满足：

闭环系统式（7）和式（9）满足全局固定时间稳定，收敛时间Tmax满足：

2.2 稳定性分析

本节将对定理1进行严格推导证明。

证明方法可分为3个部分。

1） 第一步：首先，选择一个C1正定Lyapunov函数V1(s1)的导数可以计算为：

式中：是需要设计的虚拟控制器；s1、s2为式（8）给出的滑模变量；常数参数ρ、r1、r2满足2.1 中条件。定义并且选择虚拟控制器为：

2） 第二步：选择Lyapunov函数

式中常数参数ρ、a1、r2、τ满足2.1 中条件。根据文献［27］可知，Lyapunov 函数V2为C1正定的。定义V2的导数满足：

式中：u为控制器；a和b为平滑函数。

命题1不等式（19）成立

式中：c1(β0)为固定的正常数；c2(s1)、c3(s1)为正函数。

将式（19）代入到式（18），可得：

由ξ1和的定义可得：

因此，控制器函数可以写成：

因此，将式（22）代入式（21）可得：

因此，V2满足：

注意到2ρ(2ρ-τ)＜1，对式（23）使用引理3可以得出：

对式（25）使用引理3可得：

由式（23）以及式（26）—（27）可得：

式中η1和η2由定理1 给出。容易证明

根据引理4 可知，存在固定时间Tmax不依赖于初始状态，使得在∀t≥Tmax情况下都有V2≡0 ⇒s1≡s2≡0成立。由此，定理1证明完毕。

文献［28］已经提出了一种变增益固定时间二阶滑模控制算法。一方面，文献［28］要求未知函数b的上界已知，因此相比本文所采用的假设1更为严格。另一方面，文献［28］中的控制器和本文的也大为不同。本文控制器包含两个连续项，而文献［28］中的控制器只包含一项。在附加连续项的帮助下，本文控制器中的不连续项增益函数只需用来抑制输入通道不确定项，因此和文献［28］相比，本文的控制器具有更小的不连续控制增益，从而有助于进一步削弱抖振现象。

由式（17）可知，定理1 中所提控制器的收敛时间是可调节的。选择合适的参数α0、β0，收敛时间Tmax可以为任意小的值。

3 模拟仿真

为了验证所提出的SOSM算法的准确性，通过模拟仿真测试了基于本文控制器的闭环DC-DC 降压变换器系统。对DC-DC降压变换器进行参数设置如表1所示。为了进行仿真，干扰设置为d(t)=0.1sin(2t)，其上界为dmax= 0.1。根据定理1，本文设计的全局固定时间SOSM控制器常数参数如表2所示。

表2 可变增益SOSM控制器常数参数设置Tab.2 Parameters settings of variable gain SOSM controller constant

DC-DC 降压变换器被广泛应用于电力、通信、家电、铁路交通、工业控制等领域中。本文所提出的SOSM 算法对于闭环DC-DC 降压变换器系统的控制具有普遍适用性，因此在模拟仿真测试中并没有给出具体的应用环境，而是将变换器常见的故障干扰等问题以外部信号的方式出现在模拟仿真中，以此来辨别本文所提出算法的优势。实际上，不同的应用场景意味着系统具有不同的负载电阻。

根据表1 与表2 提供的各个参数，滑模变量为s1=V0- 12，s2=ṡ1，控制器中(t，x)和分别为：

函数、的表达式为：

c1(β0)、c2(s1)、c3(s1)可具体表示为：

因此有：

可得SOSM控制器的具体表达式为：

基于上述选择的参数和函数，将通过MATLAB软件来仿真模拟。首先，将本文设计控制器分别与有限时SOSM 控制器与PID 控制器比较控制效果。根据文献［29］，有限时间SOSM控制器设计为：

式中：滑模变量s=V0-Vref；β1= 10。同时，根据线性控制理论，PID控制器设计为：

式中：KP= 13，KI= 100，KD= 0.01。采样时间设置为1 ms，初始状态选择为(iL(0)，V0(0))=(0，0)。

本文比较了所提出的可变增益固定时间SOSM控制器、有限时间SOSM 控制器和传统PID 控制器之间的控制性能。状态启动后，观察从启动时间t= 0 s 以后，系统的输出电压从0 V 稳定到跟踪参考电压的瞬态性能和稳态性能，以此来判断控制器的控制性能。除此之外，考虑到在实际操作中，参考电压Vref可能不是恒定不变的，可能会需要在运行过程中修改参考电压Vref。所以在模拟仿真中，在1 s 时将参考电压Vref进行修改，观察控制器是否能做出应对。选取参考电压Vref满足式（36）。

仿真结果如图2 所示，可变增益固定时间SOSM 控制器、有限时间SOSM 控制器和PID 控制器从启动到达到稳态的时间大约在0.15 s、0.18 s和0.26 s。可以明显发现可变增益固定时间SOSM控制器不仅响应速度快，超调量也更小，控制性能更强。除此之外，在面对参考电压Vref陡变时，3类控制器虽然都很快做出响应，但从曲线走向可以看出可变增益固定时间SOSM 控制器还是比另外两种控制方式稍快。在3 类控制器的比较中可以发现，可变增益固定时间SOSM 控制器不管在正常启动后还是运行过程中系统参考电压Vref陡变时，都具有最优的瞬态性能和稳态性能。事实上，通过调整参数可以稍微改善有限时间SOSM 控制器和PID 控制器的启动性能，但干扰抑制会变得更糟。

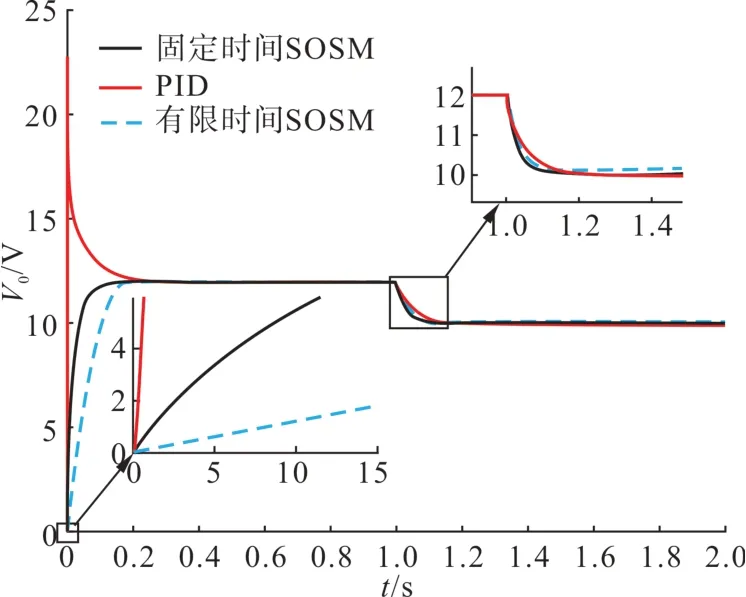
图2 PID控制器、有限时间SOSM控制和可变增益固定时间SOSM控制器下输出电压V0的仿真结果Fig.2 Simulation results of output voltage V0 under PID controller, finite-time SOSM controller and variable gain fixedtime SOSM controller

考虑在实际应用中会因为器件老化等原因存在一定的故障干扰。所以在进行模拟仿真时，引入ΔR= 10 Ω 作为系统电阻R故障时产生的误差，被控对象表达式改为：

将电阻负载器件故障扰动前后3 种控制方式下的输出电压V0进行对比，模拟结果如图3 所示。从图3中可以发现，在被控对象发生变化后，ΔR对于3 种控制器都是未知的，所以在t= 1：1.1s时，输出电压V0出现明显的抖动。并且可变增益固定时间SOSM 控制器的抖动幅度明显低于有限时间SOSM控制器和PID 控制器的抖动幅度。但当ΔR消失后，3 种控制器开始恢复稳态，固定时间的SOSM 控制器的回复稳态的响应时间也比有限时间SOSM 控制器和PID 控制器更短，表明可变增益固定时间SOSM控制器具有更好抗干扰性。

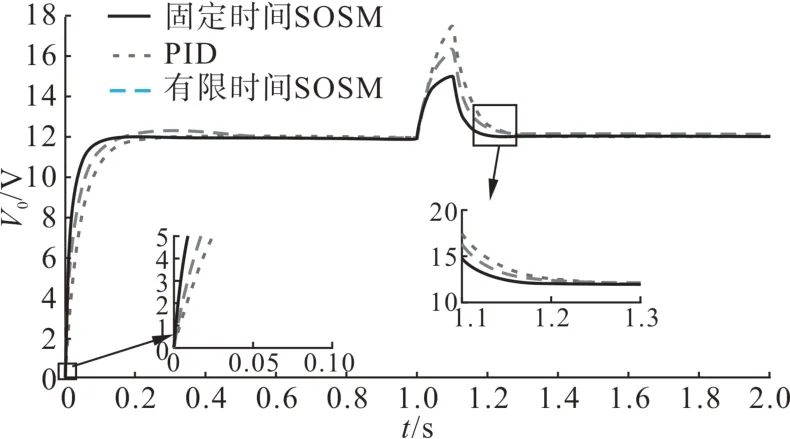
图3 电阻器件故障扰动前后3种控制方式输出电压V0对比Fig.3 Comparison of output voltage V0 of three control modes before and after disturbance of resistance device fault

除此之外，本文在模拟仿真时，还考虑了由于外部干扰导致输入电压Vin失效的情况，被控对象表达式改为：

将输入电压Vin失效前后3种控制方式下的输出电压V0进行对比，模拟结果如图4所示。由于在t=1 1.1s时，Vin= 0 V，所以3种控制方式无论怎么迭代都会被抵消为0，无法起到控制作用。因此3种控制方式下的输出电压V0在这段时间内是基本一致的，都是上下波动并逐渐趋向于收敛到某一个值。但当将输入电压Vin恢复正常后，3 种控制方式开始正常工作。从3 条曲线进行对比，固定时间的SOSM 控制器的回复稳态的响应时间还是比有限时间SOSM控制器和PID 控制器更短。所以可以得出结论：可变增益固定时间SOSM控制器具有最佳性能。

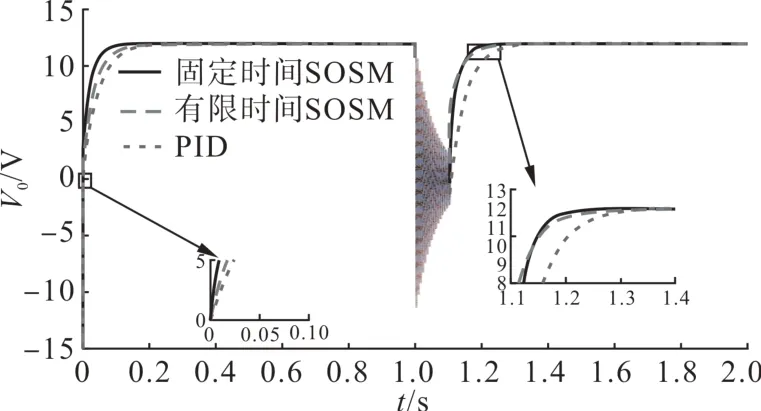
图4 输入电压干扰前后3种控制方式输出电压V0对比Fig.4 Comparison of output voltage V0 of three control modes before and after input voltage interference

本文还验证了常数参数α0、β0如何影响闭环系统的收敛。根据式（17）可知，只保留α0、β0，其余参数根据表2进行计算，收敛时间Tmax满足：

当保持其中一项不变，则另一项与Tmax呈负相关。

相应的模拟结果如图5—6所示，分别显示了其他常数参数不变只有α0、β0变化的SOSM控制器下输出电压和滑动变量S的响应曲线。从两幅图中可以清楚地观察到，随着α0、β0的增加，收敛时间缩短。

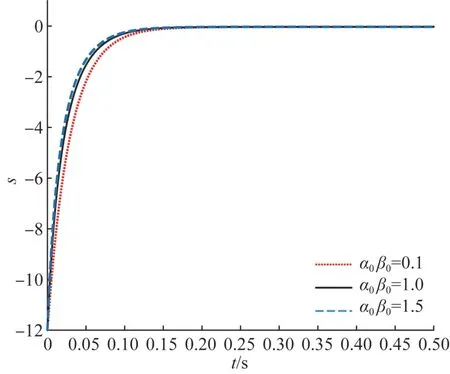
图6 可变增益固定时间SOSM控制器在常数参数α0、β0变化，其他参数不变的条件下，滑模变量S的仿真结果Fig.6 Simulation results of sliding mode variable S for variable gain fixed-time SOSM controller under the condition that constant parameters α0、β0 change and other parameters remain unchanged

本文所提算法是在充分考虑理想电路模型和实际电路模型差异的前提下设计的，因此在实际电路应用中具有更高的可行性。现有的大部分模拟仿真所考虑的数学模型［30-32］都是实际模型根据其运行原理的理想化表示。但在实际情况下，变换器的参数存在一定误差，存在不确定性。此外，外部干扰也会对模型产生影响。本文在充分考虑了参数不确定和外部干扰对系统影响的情况提出了一种新的固定时间变增益二阶滑模控制算法，该算法的设计背景更符合实际电路的运行情况，因此在实际应用中具有更高的可行性。通过与已有算法进行仿真比较，证明了本文所提算法的优越性。后续将考虑在实际应用中验证所提算法的有效性。

4 结语

本文对于DC-DC 降压变换器提出了一种新的可变增益固定时间SOSM 控制器。通过Lyapunov分析表明，可以发现本文所设计的控制器有如下两个优势：首先，即使存在参数未知以及具有函数上界的集总干扰，本文所提控制算法可以实现固定时间收敛，收敛时间不依赖于系统初始条件，因此与传统的有限时间收敛相比具有更广泛的应用；除此之外，本文将干扰的常数上界拓展到干扰的函数上界，将原来的误差只能收敛到原点的邻域内变为精确收敛到0，准确性得到极大的提高。