郑峰椿 汤靖师（ 南京大学天文与空间科学学院 南京 00）

（2 现代天文与天体物理教育部重点实验室 南京 210023）

（3 南京大学空间环境与航天动力学研究所 南京 210023）

1 引言

分析法轨道预报由于具有较大的速度优势而被广泛应用于近地天体动力学研究中, 在构造轨道分析解时除了计算二体引力还需要考虑地球非球形引力、日月第三体引力、大气阻力、太阳光压等摄动力的作用, 其中地球非球形引力摄动影响最大, 与二体引力相比量级约为O（10-3）. 地球非球形引力摄动函数一般以地固坐标系中卫星的球坐标进行计算, 若将球坐标转换为卫星轨道根数, 那么函数表达式中可分离出只包含轨道倾角的倾角函数, 而倾角函数是田谐项摄动解的重要组成因子.

在近地天体动力学领域, Kaula[1]最先提出倾角函数的概念并记为Flmp（I）, 表达式为关于sinI和cosI的三重求和多项式, 其中I是轨道倾角,l、m、p是倾角函数的3个指标, 其取值范围为2 ≤l≤L,1 ≤m≤l, 0 ≤p≤l,L即地球引力场阶次. 之后Izsak[2]给出更加简洁的公式Kjnm（I）, 指标n、j分别对应了l、p, 只需要对sin和cos作一重求和.在此基础上Allan[3]改写了相应符号而保持公式结构不变, 得到迄今为止最泛用的倾角函数表达式,公式如下:其中v为求和指标.

尽管此公式已足够简洁,但在田谐项摄动解中,倾角函数需要多重求和, 在引力场阶次较高时计算效率低, 且会出现损失精度的情况. Gooding[4–5]提出另一种递推计算方法, 将归一化倾角函数分解为两个函数的乘积, 公式如下:

其中是关于sinI和cosI的多项式, 而则是关于sin和cos的多项式, 并可以通过三项递推公式计算, 即Gooding递推公式[4–5].与关系为:

其中Nlm为归一化因子,k=l -2p. 值得注意的是倾角函数第3个指标无论使用p还是k都可以, 本质上没有差别, 而Gooding等[5]指出虽然k取值不连续, 但倾角函数关于k的正负具有对称性, 在递推计算时可借此减少计算量. 此外Gooding等[5]对递推算法做出进一步优化, 并将分离出不含倾角的因子以递推方法计算, 解决了在高阶次情况下出现上溢和下溢的问题. 同时Gooding等[5]还给出了倾角函数1阶、2阶偏导数的计算公式, 并证明了按照（2）式计算倾角函数时效率最高且具有高稳定性, 因此Gooding递推公式得到了广泛应用, 成为其他计算方法的衡量标准.

在文献[4–5]中Gooding等人并没有详细给出递推公式的证明, 吴连大等[6–7]分别利用超几何级数的递推关系和Jacobi多项式的递推关系, 完成了公式推导, 并指出其实质为Jacobi多项式的递推. 之后吴连大等[8–9]在Gooding递推方法的基础上提出计算倾角函数的改进Gooding方法, 按照文中给出的标准递推过程计算, 而对于V klm则将Gooding[4]提出的表达式进行改写并直接计算, 同时避免了出现上溢和下溢的情况. 测试结果表明改进Gooding方法计算速度更快、计算精度和稳定性也有所提高, 另一方面倾角函数的计算程序也更加简洁, 因此在分析法轨道预报过程中可以使用改进Gooding方法计算倾角函数.

在分析法轨道预报过程中地球非球形引力摄动解的计算占据了较大比重, 而田谐项摄动分析解中需要大批量计算倾角函数, 因此倾角函数的计算速度很大程度上影响了分析法预报耗时. 本文第2节以改进Gooding方法为基础, 对附加的Fortran程序进行改进, 进一步提升了大批量计算倾角函数的效率,为了方便,本文称此方法为网格Gooding法.

一般情况下, 对地球卫星作轨道预报时预报弧段不会太长, 预报过程中轨道倾角的变化量∆I很小, 因此可以将倾角函数在初始倾角I0处作泰勒展开, 以1阶或2阶展开式计算倾角函数. 倾角函数展开式为关于∆I的线性或2次多项式, 与改进Gooding法相比,一方面计算效率得到大幅提升,但另一方面展开式存在一定的截断误差, 从而导致分析法预报精度受到影响. 如果展开式误差带来的轨道预报结果偏差在一定范围内, 那么在分析法预报过程中可以使用展开式计算倾角函数, 从而很大程度地提高预报速度, 对大量目标作轨道预报时利用此方法可极大减轻工作量. 本文第3节分析了不同初始倾角、地球引力场阶次、倾角变化量对倾角函数展开式误差的影响, 比较了分别精确至1阶、2阶时展开式的计算速度以及精度. 第4节设计若干算例, 在分析法轨道预报中分别使用网格Gooding法、1阶、2阶展开式计算倾角函数, 以改进Gooding方法为基准, 分析预报星历偏差以及预报耗时,其中预报星历为J2000平赤道坐标系下的直角坐标.

2 倾角函数递推算法介绍与程序优化

由于吴连大等[8–9]提出的改进Gooding方法具有计算速度快、计算精度和稳定性高、程序简洁的优点, 故可以直接应用到分析法轨道预报中, 而在实际应用中发现递推程序有进一步提升速度的空间. 根据田谐项摄动解公式可知预报过程中需要计算大批量倾角函数, 参考刘林[10]书中公式:

其中σ（2）s（t）表示轨道根数的2阶短周期项, ∆σlmpq中包含倾角函数Flmp及其1阶偏导数F′lmp, 刘林[10]给出了田谐项摄动解的具体公式, 由于公式较长,本文不再罗列. 需要注意的是改进Gooding法计算结果为归一化倾角函数, 而常用的分析解中倾角函数为非归一化的,所以实际计算时需对其进行转换.

根据（4）式, 由l≤L可知倾角函数计算次数取决于地球引力场阶次, 递推次数N可由下式计算,

这表示至少需要循环调用N次递推程序, 而根据改进Gooding法原理可知在递推过程中可计算出若干倾角函数, 如果能够记录下这些值, 那么在循环过程完全可以跳过这次计算,从而减少程序调用次数.当引力场阶次较高时, 将节省不少倾角函数的计算时间.

同Gooding递推方法一样, 吴连大等[8–9]将倾角函数分解为（2）式的形式, 按照标准过程递推计算, 不同的是改写了表达式并直接计算, 因此在批量计算时只需考虑的程序改进, 其递推公式为:

其中x= cosI, 0 ≤J≤l, 公式沿着l递推, 递推初值为其中q= max（m,k）. 该递推关系成立的条件为k≥0, 在k <0时可以利用倾角函数的对称性直接计算, 如（7）式所示:

根据（6）式可知, 倾角函数在沿着l方向递推过程中可得到中间值（q≤z≤l）, 由（2）式和（4）式可知这些中间值正是田谐项摄动分析解计算中所需要的, 而对递推程序的改进原理为将其记录下来以避免在循环过程中重复计算.

递推程序改进的具体方法为将倾角函数以3维数组形式作为函数接口. 在吴连大等[8–9]给出的程序中, 函数输入接口为轨道倾角和3个指标l、m、k, 输出接口为倾角函数及其偏导数. 修改之后输入接口为倾角、地球引力场阶次L, 输出接口为3维数组形式的倾角函数及其偏导数, 在函数内部同样为3维数组.该算法的原理很简单,规定2 ≤l≤L,1 ≤m≤l, 0 ≤p≤l, 在沿着l、m、p进行3重循环过程中将p转换为k, 以改进Gooding法计算倾角函数, 并将、分别赋给3维数组A[l][m][p]和F[l][m][p].每次计算之前对A[l][m][p]进行检验,如果已经被赋值, 则跳过该过程, 并且在计算倾角函数时直接引用A[l][m][p]. 改进之后仍需计算N次, 而的计算次数减少, 因此倾角函数的计算耗时有所缩减, 且随着阶次的增加, 耗时减少比例逐渐增大. 由于该算法本质为使用改进Gooding法计算倾角函数并在3维网格中赋值, 因此精度并未改变, 为了方便, 本文中称其为网格Gooding法.

吴连大等[8–9]测试了1–200阶倾角函数的计算时间, 与Gooding方法相比, 使用此方法时效率提升了41%. 本文设计若干算例, 对改进后程序的计算效率进行评估, 考虑到在分析法预报中地球引力场取50阶即可获得高精度星历, 因此L选取10、50, 每组设置10个倾角, 选取0.1◦、10◦、20◦、···、90◦, 分别按照改进Gooding法和网格Gooding法批量计算倾角函数及其偏导数, 且重复计算10次, 并记录平均耗时, 其中两种算法都以C++语言实现.表1给出计算机配置以及编译设置, 所有算例均以Release模式进行测试. 相比之下, 随着L增大, 网格Gooding法的计算效率逐渐提高,L取10、50时计算耗时分别缩短了18.8%、23.8%（若将此方法应用到分析法预报中, 预报耗时可参考本文第4节中的表5）.

3 倾角函数的展开式分析

3.1 倾角函数展开式

根据（1）式可知在3个指标不变时倾角函数为关于sin和cos的多项式, 若已知初始倾角I0处的倾角函数及其偏导数, 则可以在I0附近进行泰勒展开,以展开式计算倾角函数及其1阶偏导数, 如下式所示:

通常情况下, 分析法预报的弧段较短, 轨道平倾角变化幅度一般较小, 在3天弧段以内基本不超过0.01◦, 因此在分析法预报中能够对倾角函数作泰勒展开, 以t0时刻的倾角函数（I0）及其1阶、2阶偏导数为初值, 在t时刻使用展开式计算倾角函数. 倾角函数及其偏导数初值通过改进Gooding法计算, 由于只提供2阶以内的初值, 因此倾角函数展开式最高可以精确到2阶,而偏导数只能展开至1阶.

以泰勒展开式计算倾角函数可大幅提高计算速度,从而有效缩短分析法预报耗时.与改进Gooding法相比, 尽管使用网格Gooding法计算大批量倾角函数能在保持精度不变的同时提高计算速度, 但在轨道预报过程中倾角函数的计算只是其中一部分, 因此预报速度虽有所提升, 但并不明显. 展开式进一步大幅减小了倾角函数的计算量, 经测试在地球引力场取50阶时,与网格Gooding法对比,1阶、2阶展开式的计算耗时均缩短了99%以上, 因此不难理解以展开式计算倾角函数能够显著提高分析法预报效率.

虽然泰勒展开方法可以有效提高计算效率, 但是计算精度却受到一定影响. 由（8）式可知, 展开式存在截断误差, 倾角函数精度降低, 从而导致预报结果产生偏差. 只有当截断误差较小、预报星历偏差不足以影响预报精度时, 才可以将倾角函数展开式应用到分析法轨道预报中.

3.2 展开式误差分析

吴连大等[8–9]已经验证改进Gooding法的精度相比Gooding法更高一些, 而网格Gooding法计算结果与改进Gooding法一致, 因此可以将其作为计算倾角函数的精度对比标准. 倾角函数展开式误差按照下式计算:

其中ε1为倾角函数1阶展开误差,ε2为2阶展开误差,ε′为倾角函数偏导数1阶展开误差, 其中各项初值通过网格Gooding法计算得到.

3.2.1 算例

根据（9）式可知倾角函数展开式的误差主要与初始倾角I0、倾角变化量∆I以及3个倾角函数指标有关, 为了较为全面地分析倾角函数展开式的精度与这3种影响因素的关系, 我们设计了若干算例如表2所示. 其中地球引力场阶次取为50, 指标l取值范围是2 ≤l≤50, 初始倾角I0从1◦起每隔1◦取值至179◦, 此外也设置了0.01◦及179.99◦, 总共181组取值, 倾角变化量∆I分别取为0.1◦、0.01◦、0.001◦,倾角函数展开式精确至1阶、2阶, 分别使用泰勒展开方法和改进Gooding法计算倾角函数, 通过这些算例分析其计算结果偏差. 在实际应用场景中, 对于近圆轨道, 当地球引力场阶次取50, 使用完整力模型时, 以分析方法预报3天后的平倾角变化量基本小于0.01◦, 因此∆I选择0.01◦为标准. 倾角函数共有3个指标, 这里不再详细讨论m、p, 仅计算各阶次l的倾角函数误差最大值.

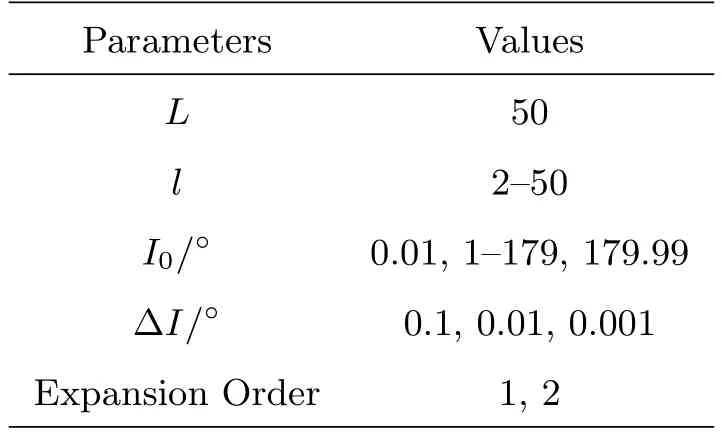
表2 倾角函数展开式误差分析算例参数设置Table 2 Parameters setting for the error analysis test of the inclination function expansion

3.2.2 计算结果

由于倾角函数1阶、2阶展开计算速度差别很小, 而2阶展开式精度更高, 因此主要分析不同初始倾角和倾角变化量对2阶展开式误差的影响, 并简单对1阶、2阶展开式误差进行比较. 2阶展开式的误差计算结果见图1, 分别表示∆I取不同角度时倾角函数2阶展开式（左列）及其偏导数1阶展开式误差最大值（右列）的等高线图, 其中误差值取对数, 横轴为指标l, 纵轴为初始倾角I0. 由图1可知随着l增加, 倾角函数2阶展开误差逐渐增大, 而根据等高线分布密度可知误差增大速度逐渐降低. 另一方面在l <20时, 误差大小几乎不受初始倾角的影响,l≥ 20时, 误差随着初始倾角增加而减小, 当超过90◦之后又逐渐增大, 并且很明显可以看出等高线关于I0=90◦对称. 倾角函数偏导数1阶展开的误差分布与上述规律基本一致, 只是误差更大. 图2为倾角函数1阶展开误差结果, 表示∆I取为0.01◦时展开式误差最大值的等高线图, 误差取对数, 横轴为指标l, 纵轴为初始倾角I0. 根据图1 （d）与图2结果,倾角函数偏导数的1阶展开误差约为倾角函数1阶展开误差的30倍.

图2 倾角函数1阶展开式的误差最大值等高线图Fig.2 Contour diagram for maximum error of 1st-order expansion of the inclination function

通过图1中6个子图的对比可知, 倾角函数及其偏导数误差随着∆I增加而增大, 并且∆I每增加10倍, 倾角函数误差增大约1000倍, 而偏导数误差增大约100倍, 这与展开式的截断误差是∆I的n次幂相关, 为便于理解, 将（9）式整理为如下形式:

据此可知倾角函数及其偏导数的展开式误差分布和2阶或3阶偏导数分布是一致的.

根据计算结果显示, 倾角函数展开误差受指标l和倾角变化量∆I的影响较大,l越大误差越大,而从（10）式可以直观看出误差与∆I具有幂次关系.另外初始倾角对误差影响较小, 尤其是l<20时, 随着I0增加, 误差几乎没有变化. 通过对比图1 （c）和图2可知倾角函数2阶展开相比于1阶展开误差减小了约3个量级. 上述分析全部基于误差最大值进行, 尽管该结果不能完全体现出倾角函数展开误差在（l,m,k）空间的分布特征, 但由于在田谐项摄动分析解计算时倾角函数误差最大值更能反映对计算精度的影响, 所以上述结果已经足够用来分析倾角函数展开式的适用场景了. 对于预报弧段较短、平倾角变化量较小的轨道, 当地球引力场取较低的阶次时, 在分析法预报中可以尝试将倾角函数以2阶展开式计算, 此时预报误差相对较小, 不过实际应用结果需要使用大量算例进行测试才能进一步分析.

4 分析法轨道预报误差分析

分析法轨道预报中使用展开式计算倾角函数可有效提高预报速度, 但不可忽视展开式存在较大误差, 而由（4）式可知在计算田谐项摄动分析解时误差会在三重求和过程中逐渐累积, 并最终导致预报结果产生偏差. 虽然根据图1与图2可以初步分析倾角函数展开式的适用场景, 但为了进一步分析实际应用中的预报精度, 需要使用大量算例作轨道预报测试. 一般情况下分析法预报误差比较大,预报24 h的误差为数十米至数百米不等, 而倾角函数展开导致的预报误差并没有这么大, 如果直接将展开后的预报结果与数值法预报结果比较, 则可能被分析法预报本身的误差掩盖. 由于展开式误差不确定正负, 实际计算中可能出现展开式的预报精度比完整算法更高的“假象”, 因此以数值法预报星历作为标准无法准确评估展开式的预报精度. 因为整个预报过程中只有倾角函数的计算方法不同, 所以直接比较展开前后预报星历的偏差即可. 本章以改进Gooding法为基准, 分别将倾角函数展开式精确到1阶和2阶, 对预报星历偏差进行分析, 另一方面,为定量比较倾角函数展开前后分析法预报的速度,设计了若干算例, 并记录预报耗时.

4.1 精度分析算例

倾角函数展开式误差的影响因素为初始倾角I0、倾角变化量∆I和阶次l, 而阶次l的取值范围与地球引力场阶次有关, 因此选择不同的初始轨道, 分析初始倾角I0和地球引力场阶次L对预报星历偏差的影响. 由于∆I是在轨道预报过程中计算的, 无法通过给定初值分析, 所以不再考虑此因素.由于田谐项摄动分析解公式中存在因子（）l, 所以容易理解轨道半长径a越大倾角函数展开误差对预报结果的影响就越小, 因此主要选取低轨算例进行分析, 同时加入少量中高轨的算例, 算例的参数设置如表3所示. 分析法预报初始历元按照简约儒略日设为59000, 预报长度为3 d, 步长为30 min,L分别设5组取值, 地球参考半径为6378.137 km, 轨道高度h通过将轨道半长径a与地球参考半径相减得到, 在300 km与40000 km之间取值, 共有46条低轨与14条中高轨, 轨道偏心率均设为0.001, 初始倾角则在90◦以内每隔5◦选取了19组值, 轨道升交点经度、近地点角和平近点角均设为50◦.

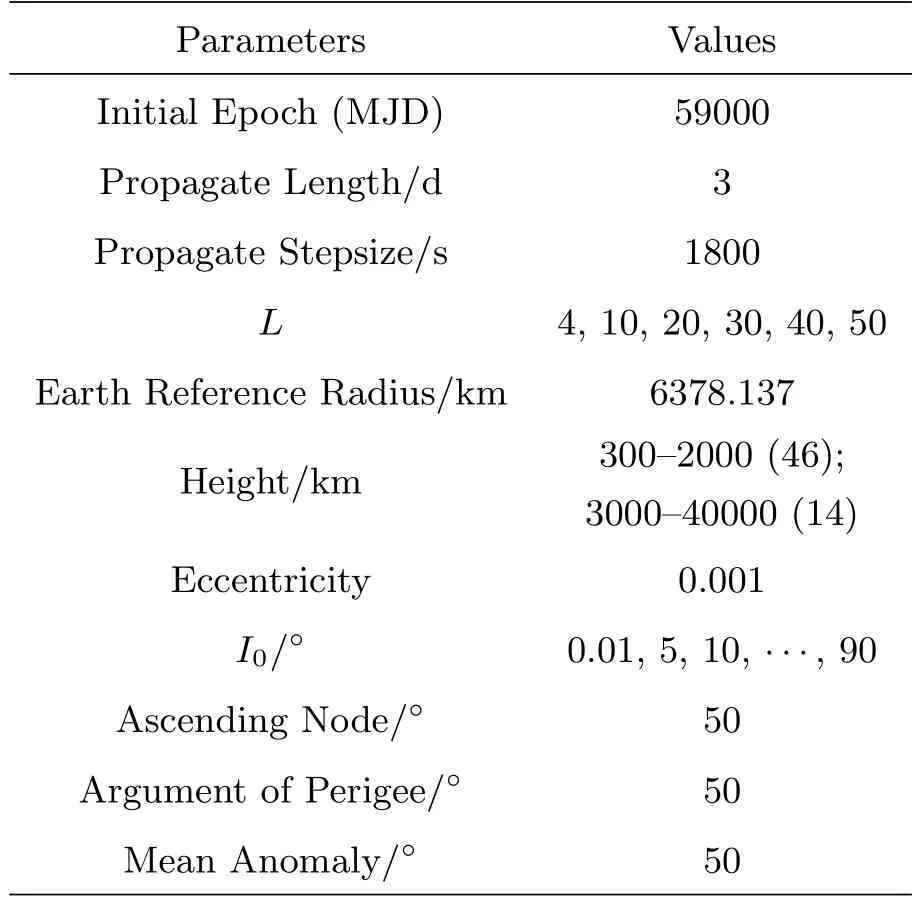
表3 分析法预报精度分析算例参数设置Table 3 Parameters setting for test of calculation accuracy of analytical orbit prediction

分析法预报所用摄动模型为完整力模型, 包括带谐项、田谐项、日月引力摄动、大气阻力摄动和光压摄动等. 一般情况下为了发挥分析法预报的速度优势, 步长设置为与预报时长相等, 而本次测试将步长设为30 min, 一方面是为了得到较密集的星历, 便于分析星历偏差, 另一方面可以更频繁地更新参考星历, 从而一定程度上提高预报精度,此外轨道预报是精密定轨过程中不可或缺的一部分, 而精密定轨中观测数据的历元间隔也决定了步长是较小的. 由于倾角函数展开误差与偏心率无关, 因此简单地选取近圆轨道进行测试, 偏心率取0.001. 根据倾角函数展开式误差分析结果可知误差关于I0= 90◦对称, 因此不再考虑初始倾角大于90◦的算例.

在计算田谐项摄动解时可能存在共振现象,即（4）式中某些项具有小分母问题（分母接近于0）,这主要取决于求和指标l、m、p、q和卫星平运动速率, 具体表达式可见文献[10]. 一般情况下地球引力场阶次越高, 满足小分母关系的求和指标越多,共振项也就越多, 另外低轨卫星会更频繁地遇见共振现象. 在本文所使用的分析法预报算法中, 计算田谐项时所有满足小分母关系的求和指标不再参与短周期项的计算.

测试中分别使用网格Gooding法、1阶展开和2阶展开这3种方法计算倾角函数及其偏导数, 遍历以上轨道预报算例, 得到3组预报星历, 即各时刻的位置矢量:接着按照下式分别计算1阶展开和2阶展开的预报星历偏差RMS:

其中Nt为星历点数量, 根据RMS结果对倾角函数展开式在轨道预报中的适用性进行分析.

4.2 算例结果分析

为研究地球引力场阶次和初始倾角与预报精度的关系, 挑选出相同轨道高度的算例, 对预报星历偏差RMS作图,并为了直观分析,将RMS取对数.另外挑选出若干初始倾角相同的算例, 比较不同轨道高度的预报星历偏差RMS, 从而分析在不同轨道高度下, 倾角函数展开对预报结果的影响. 由于倾角函数2阶展开精度更高, 且速度几乎相同, 因此主要对2阶展开的预报结果进行分析.

对于轨道高度在2000 km以内的低轨算例, 一般情况下地球引力场阶次越高, 预报星历偏差RMS越大, 只是增加幅度很小.L≤50时, 预报星历偏差RMS整体上随着初始倾角的增加有逐渐减小的趋势, 这和倾角函数误差的变化规律相符, 而在I0=90◦时RMS小幅增大.以500 km高度的轨道为例,倾角函数2阶展开的预报星历偏差如图3所示, 横坐标为初始倾角I0, 纵坐标为预报星历偏差RMS, 并取对数, 图例表示地球引力场阶次L. 由图3可知地球引力场在50阶以内时RMS小于0.5 mm, 在I0=85◦处RMS为极小值. 经过进一步计算和分析发现,由于各阶次的引力场系数和倾角函数表达式不同,不同阶次的RMS极小点存在差异, 例如L= 3时极小点在I0= 83.5◦左右, 因为田谐项分析解为各阶次计算结果的和, 所以图3中极小点为综合结果, 并不严格在90◦处.

图3 500 km高度轨道在取不同初始倾角时, 倾角函数2阶展开的分析法预报星历偏差Fig.3 The ephemeris deviations of analytical orbit prediction for 500 km altitude orbit that have different initial inclination with inclination function calculated by 2nd-order expansions

对于中高轨算例, 地球引力场阶次对预报误差影响很小, 而随着初始倾角增加, 轨道高度不同时,预报星历偏差RMS具有不同的变化规律, 但RMS整体很小. 比如轨道高度为10000 km算例的RMS随初始倾角增加而逐渐增大, 而高度为36000 km的同步轨道算例的RMS却有所浮动,如图4所示,不过二者RMS均不超过10-7m.

另一方面为更清晰地分析预报误差与轨道高度h的关系, 取L= 50, 将预报星历偏差RMS关于h作图. 轨道高度小于和大于2000 km, 结果分别如图5、图6所示, 其中横坐标为h, 纵坐标为预报星历偏差RMS的对数值, 图例表示初始倾角I0. 可以发现当轨道高度小于2000 km时, RMS随轨道高度增加而逐渐减小, 但随着初始倾角增加而减小, 且均小于1 mm. 而当轨道高度大于2000 km时, RMS先随轨道高度增加而减小, 然后逐渐增大并维持在10-8m至约10-7m之间.

图5 不同高度的低轨倾角函数2阶展开的分析法预报星历偏差Fig.5 The ephemeris deviations of analytical orbit prediction for Low Earth Orbit at different altitude with inclination function calculated by 2nd-order expansions

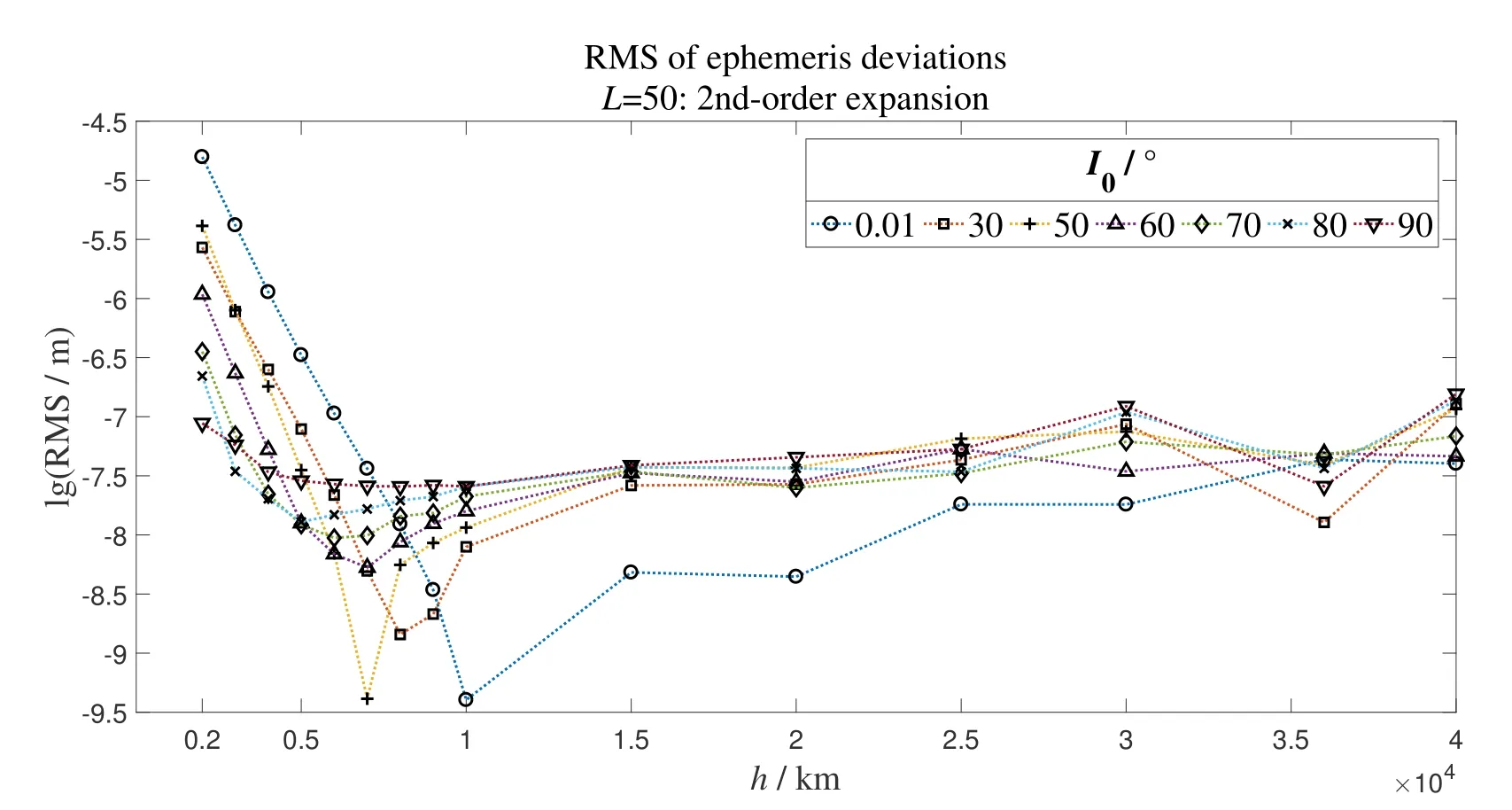
图6 不同高度的中高轨倾角函数2阶展开的分析法预报星历偏差Fig.6 The ephemeris deviations of analytical orbit prediction for Medium-High Earth Orbit at different altitude with inclination function calculated by 2nd-order expansions

通过上述算例结果可知,在分析法轨道预报中,当地球引力场不高于50阶时, 以2阶泰勒展开式计算倾角函数, 与改进Gooding法相比, 低轨卫星的预报星历偏差RMS小于1 mm, 而中高轨卫星则更小, 以地球同步轨道卫星为例, RMS约为10-7m.在实际应用场景中, 分析法预报一般不需要使用高阶次的地球引力场模型, 50阶已经足够满足精度要求, 由于分析法预报24 h的位置误差一般大于10 m量级, 因此可以认为倾角函数2阶展开不会影响分析法预报精度.

4.3 分析法预报速度分析

为定量比较倾角函数展开前后分析法预报的效率,设计若干算例进行分析,参数设置如表4所示.由于分析法预报耗时受轨道半长径影响很小, 主要取决于地球引力场阶次的大小以及预报节点的数量, 因此轨道半长径不需考虑, 引力场阶次分别取6个, 预报时长和预报步长分别设为3 d、30 min, 共有144个预报节点. 摄动模型依然为完整力模型, 轨道偏心率为0.001, 初始倾角在1◦–90◦之间间隔1◦取值.

测试环境同样如表1, 以Release模式编译程序.分别使用改进Gooding法、网格Gooding法、1阶展开和2阶展开4种方法计算倾角函数, 在L取不同值时, 分别对不同初始倾角的90组算例进行预报, 记录预报耗时并求和,并以改进Gooding法为基准,计算其余3种方法的耗时减小比例. 统计结果如表5所示, 网格Gooding法使得分析法轨道预报速度有小幅提升, 在L较高时预报耗时减少13%左右, 而1阶、2阶展开对预报速度的提升效果十分显著, 且二者差别很小, 随着L的增加预报耗时减小比例逐渐增大,L= 50时达到48%左右. 因为分析法预报中除了倾角函数还有其他各种计算, 因此预报耗时的减小存在上限, 根据测试结果分析, 倾角函数的计算耗时约占预报总耗时的50%, 因此当L增加时, 预报耗时最多可减少约50%.

5 结论

本文基于改进Gooding法调整了倾角函数的计算程序, 使其能够一次性作大批量计算, 在计算50阶以内的倾角函数时, 相较于循环调用程序, 使用网格Gooding法耗时缩短了23.8%.

考虑到倾角函数计算公式为多项式, 可以进行泰勒展开, 而在短弧轨道预报中平倾角变化量一般很小, 所以本文对倾角函数展开式的计算精度进行分析, 发现2阶展开式精度更高. 为了研究倾角函数展开式应用到分析法轨道预报中的可行性, 设计了大量算例, 在预报过程中分别使用改进Gooding法和1阶、2阶展开式计算倾角函数, 分析预报星历偏差RMS. 根据测试结果, 在地球引力场取50阶以内时, 倾角函数2阶展开后, 低轨卫星的预报星历偏差RMS小于1 mm, 而随着轨道高度增加, RMS呈减小的趋势. 一般在分析法预报中, 地球引力场阶次取值较低, 基本不会超过50阶, 因此将倾角函数作2阶展开并不会影响分析法预报精度.

在计算耗时方面,与改进Gooding法相比,网格Gooding法的预报速度有小幅提升, 而1阶、2阶展开对预报速度的提升效果更加明显, 且二者速度几乎相同. 另一方面3种方法的预报耗时减小比例随着地球引力场阶次的增加而增大, 在50阶时分别达到14%、49%、48%.