一致分数阶时滞微分方程边值问题解的存在性与唯一性
2023-09-27周文学黎文博
张 敏, 周文学, 黎文博
(兰州交通大学 数理学院, 兰州 730070)
0 引 言
分数阶微分方程的边值问题是分数阶微分系统理论的重要课题. 目前, 对分数阶微分方程边值问题的研究已取得了丰富成果, 其中最主要的是基于Riemann-Liouville和Caputo分数阶导数的定义[1-9]. 但这两种导数均不满足经典链式法则, 并且这两种导数的某些性质使得分数阶导数的应用很困难. 因此, Khalil等[10]提出了一种新的分数阶导数和分数阶积分的定义, 称为一致分数阶导数和积分. 这种新的分数阶导数的定义可满足经典的分数阶导数不能满足的一些性质, 如乘积法则、 商法则、 链式法则、 罗尔定理和中值定理等, 并且其在生物物理学、 电容理论、 控制理论和实验数据拟合等领域应用广泛[11-13]. 但对带有时滞的分数阶微分方程边值问题的研究目前报道较少[14-16]. Yang等[17]利用Schaefer不动点定理和Krasnoselskii’s不动点定理研究了一类非线性分数阶微分方程边值问题
正解的存在性, 其中0 解的存在唯一性, 其中1 基于上述研究, 本文利用Leray-Schauder度理论和Banach压缩映射原理考虑如下一类一致分数阶时滞微分方程边值问题: (1) 解的存在性与唯一性, 其中1<β≤2,τ>0,f: [0,1]×→是连续函数,是阶数为β的一致分数阶导数. 定义1[10]假设函数f: [0,∞)→, 则f的β∈(n,n+1]阶一致分数阶导数定义为 (2) (3) 注2由一致分数阶导数定义可知, 当β=1时, 一致分数阶导数定义即为传统的一阶导数定义. 引理1[10]当β∈(n,n+1]并且f在t>0处n+1阶可微时, 有 (4) 定义2[19]假设函数f: [0,∞)→, 则f的β∈(n,n+1]阶一致分数阶积分定义为 (5) 引理2[19]假设函数f: [0,∞)→连续, 并且β∈(n,n+1], 则有 DβIβf(t)=f(t). (6) 引理3[19]假设f: [0,∞)→是β阶可微函数, 并且β∈(n,n+1], 则有 IβDβf(t)=f(t)+a0+a1t+…+antn, (7) 其中ai∈,i=0,1,2,…,n. 引理4设函数f: [0,1]×→是连续的,u(t)是边值问题(1)的解, 则 (8) 其中格林函数G(t,s)为 (9) 证明: 由引理3知, 有 (10) a0+a1=0; (11) 根据u(1)+u′(1)=0, 有 (12) 结合式(11),(12)可得 (13) 将式(13)代入式(10)可得 引理5(Arzela-Ascoli定理)[20]集合P⊂C([a,b])列紧的充分必要条件为: 1) 集合P有界, 即存在常数ψ, 使得对∀u∈P, 有|u(t)|≤ψ(∀t∈[a,b]); 2) 集合P等度连续, 即对∀ε>0, 始终存在σ=σ(ε)>0, 使得对于∀t1,t2∈[a,b], 只要|t1-t2|<σ, 即有|u(t1)-u(t2)|<ε(∀u∈P). 设A为C([-τ,1],)按范数构成的Banach空间, 在A上定义一个算子Q, 假设条件: (H1) 函数f∈C([0,1]×,), 并且φ∈C([-τ,0],); (H2) 存在常数α,B>0, 使得∀(t,u)∈[0,1]×, 有|f(t,u)|≤α|u|+B; (H3) 存在函数η(t)∈L1/2([0,1],+), 使得∀t∈[0,1], 当任取u,v∈时, 有|f(t,u)-f(t,v)|≤η(t)|u-v|, 其中 证明: 由函数G(t,s),f(s,u(s-τ))的连续性可知算子Q是连续的, 并且易证Q(A)⊂A.设P是A中的一个有界集, 则存在常数M>0, 使得对任意的u∈P, 有‖u‖≤M. 下面利用Leray-Schauder度理论证明边值问题(1)正解的存在性, 分以下3个步骤. 1) 证明算子Q(P)是一致有界的.对任意的u∈P, 有 因此, 算子Q(P)是一致有界的. 2) 证明算子Q(P)是等度连续的.对任意的u∈P,t1,t2∈[-τ,1]且t1 ① 当0≤t1 ② 当-τ≤t1 ③ 当-τ≤t1<0 在上面3种情形中, 当t1→t2时, 总有|Qu(t2)-Qu(t1)|→0, 表明Q(P)是等度连续的.故由引理5可知,Q(P)是列紧的, 从而算子Q:A→A是全连续的. 令ω=T+1,Bω={u∈A: ‖u‖<ω}, 则u≠γQu, 对任意的u∈∂Bω,γ∈[0,1].定义一个映射:Fγ(u)=u-γQu, 则Fγ(u)=u-γQu≠0, 对任意的u∈∂Bω,γ∈[0,1].因此, 由Leray-Schauder度的同伦不变性, 有 deg(Fγ,Bω,θ)=deg(I-γQ,Bω,θ)=deg(F1,Bω,θ)=deg(F0,Bω,θ)=deg(I,Bω,θ)=1≠θ. 从而根据Leray-Schauder度的可解性可知, 方程F1(u)=u-Qu=0在Bω上至少存在一个解, 进而边值问题(1)至少有一个正解.证毕. 定理2如果条件(H1)和(H3)成立, 并且‖η‖(Λ2+Λ3)<1, 则边值问题(1)存在唯一解. 下面利用Banach压缩映射原理证明边值问题(1)解的存在唯一性, 分以下两个步骤. 1) 证明Q(Bδ)⊂Bδ.对任意的u∈Bδ, 有 则‖Qu‖≤δ.表明算子Q将Bδ中的有界子集映为Bδ中的有界子集, 即Q(Bδ)⊂Bδ. 2) 证明算子Q为压缩映射.对任意的u,v∈A: ① 当t∈[0,1]时, 有 ② 当t∈[-τ,0]时, 有|Qu(t)-Qv(t)|=|φ(t)-φ(t)|=0. 由①,②可得 ‖Qu-Qv‖[-τ,1]≤‖η‖(Λ2+Λ3)‖u-v‖[-τ,1]. 因为‖η‖(Λ2+Λ3)<1, 所以算子Q为压缩映射.即由Banach压缩映射原理可知算子Q存在唯一的不动点, 故边值问题(1)存在唯一解. 考虑下列一致分数阶时滞微分方程边值问题: (14) 解的存在性与唯一性. 所以存在η(t)=e-3tsin1/2t∈L1/2([0,1],+), 满足条件(H3), 且‖η‖=0.166 7.又因为 所以‖η‖(Λ2+Λ3)≈0.571 3<1.因此根据定理2可知, 边值问题(14)存在唯一解.
1 预备知识



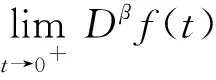




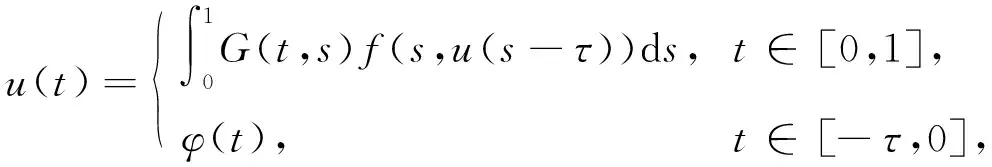
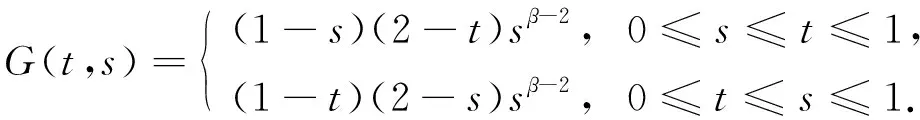
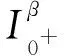



2 主要结果
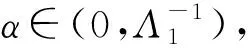
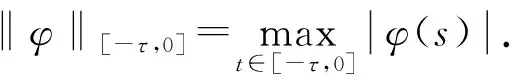
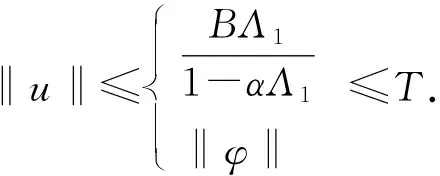
3 应用实例

