胡春安,熊昱然

(江西理工大学信息工程学院,江西 赣州 341000)

1 引言

以模拟自然界中动物种群行为为基础设计的算法被称为元启发式算法[1,2]。这些行为包括繁殖、捕猎和迁徙等。通过对这些行为进行数学建模,来解决一些分布式问题[3]。近年来,群优化算法[4]逐渐被应用于诸如图像处理、路径规划和数据挖掘等方面,并取得了相应的研究成果。目前,群智能算法发展现状已经从简单的粒子群演变到一些具有一定感知、预警和自主搜寻能力的种群。比较常见的群智能算法有粒子群优化算法[4]、蚁群算法[5]、麻雀搜索算法[6]和布谷鸟算法[7]等。群算法的基础理论提出后主要的发展方向有2个:一个是在算法的基础上进行改进,优化其中的种群行为策略;另一个是将算法应用在实际工程案例中,获得更好的优化效果。

哈里斯鹰优化HHO(Harris Hawk Optimization)算法是由Heidari等人[8]在2019年提出的一种元启发算法,源于观察哈里斯鹰和它们的猎物(兔子)之间的追逐逃跑行为。哈里斯鹰捕捉猎物的主要策略是突袭。在这个智能策略里,鹰群从几个不同的方向协同攻击检测到的正在逃跑的兔子。由于猎物存在一定的逃生能力,哈里斯鹰可能在几分钟内在猎物附近进行多次短距离的快速攻击。鹰群能根据环境和猎物的逃跑状态表现出几种不同的追逐风格。当最强的鹰(领导者)俯身冲向猎物并且迷路时,就会发生策略的转换,由鹰群中另一名成员继续追击。

与其他的元启发式算法类似,传统的哈里斯鹰优化算法本身也存在在开发阶段搜索容易陷入局部最优、收敛精度低等问题[9]。为了使算法有所改善,郭雨鑫等人[10]提出了多策略优化的哈里斯鹰优化算法,在探索阶段引入了柯西变异,局部搜索阶段引入了自适应权重粒子来更新位置,解决原始哈里斯鹰优化算法易陷入局部最优和收敛精度低的问题。马一鸣等人[11]提出了一种改进的哈里斯鹰优化定位算法,在提升原算法性能的基础上保留其寻优机制,对基于最大似然估计的适应度函数进行改进,在优化过程中达到更优的适应度值,从而提高算法的寻优精度。王归新等人[12,13]通过结合2种较新的群智能算法(改进灰狼优化算法与哈里斯鹰优化算法),从而获得了二者易实现、收敛速度快和全局搜索能力强的优点。

目前的HHO改进策略虽然在一定程度上改进了算法的寻优能力,但只是针对其中的某一种更新策略进行更改或者改变逃逸能量的变化方式,并没有有效解决寻优的盲目性。针对以上问题,本文提出了一种融合分布式估计策略、混沌局部搜索策略和精英池策略的多策略改进哈里斯鹰优化算法。

2 哈里斯鹰优化算法

哈里斯鹰优化算法通过构建数学模型来模拟现实中哈里斯鹰在不同情况下的捕猎策略,整个算法分为探索阶段和开发阶段。

2.1 探索阶段

在HHO算法中,哈里斯鹰个体是候选解,每个迭代步骤中的目标猎物为所求问题的最优解,并根据2种策略来发现猎物,如式(1)所示:

(1)

其中,t表示为当前迭代次数,X(t+1)表示第t+1次迭代时鹰的位置;Xrabbit(t)表示第t次迭代时猎物的位置;X(t)表示第t次迭代时鹰的位置;r1,r2,r3,r4,q是(0,1)的随机数;LB和UB分别表示搜索空间的下界和上界;Xrand(t)表示第t次迭代时种群中随机选择的鹰的位置;Xm(t)表示第t次迭代时鹰群位置的平均值,如式(2)所示:

(2)

其中,Xi(t)表示第t次迭代时第i只鹰的位置,N表示鹰的总数。

2.2 过渡阶段

根据猎物的逃逸能量,HHO算法可以从探索阶段转移到开发阶段。在猎物逃跑的过程中,猎物的能量是递减的,本文把逃逸能量抽象成式(3):

(3)

其中,E表示当前猎物的逃逸能量;T表示最大迭代次数;E0表示初始能量,是(-1,1)的随机数。

在每次迭代过程中,当逃逸能量|E|≥1时,进入探索阶段;逃逸能量|E|<1时,进入局部开发阶段。

2.3 开发阶段

HHO提出了4种可能的策略来模拟哈里斯鹰的攻击手段。用r来表示猎物的逃跑概率。

Case 1:软围攻。当r≥0.5且|E|≥0.5时,在这种攻击方式中,哈里斯鹰群将会对它进行软包围,使猎物更加疲惫,然后进行突袭。该行为的抽象数学模型如式(4)所示:

X(t+1)=ΔX(t)-E|JXrabbit(t)-X(t)|,

ΔX(t)=Xrabbit(t)-X(t)

(4)

其中,ΔX(t)表示第t次迭代时猎物位置与哈里斯鹰距离之差;J表示猎物在逃跑过程中的随机跳跃强度,是一个(0,2)的随机数,每次迭代中都会随机变化。

Case 2:硬围攻。当r≥0.5且|E|<0.5时,猎物此时逃逸能量低,哈里斯鹰直接进行最终突袭。在这种情况下用式(5)更新当前位置:

X(t+1)=Xrabbit(t)-E|ΔX(t)|

(5)

Case 3:累速俯冲式软围攻。当r<0.5且|E|≥0.5时,猎物仍然有足够的能量成功逃脱,在突袭之前,哈里斯鹰建立了一个软围攻策略,将Levy飞行集成进了HHO中,这个阶段的位置更新策略如式(6)～式(8)所示:

Z=Y+S·LF(D)

(6)

Y=Xrabbit(t)-E|JXrabbit(t)-X(t)|

(7)

(8)

其中,D表示当前问题的维度,S表示D的随机行向量,Y表示累速俯冲式软围攻公式计算出的位置向量,Z表示经过Levy飞行扰动过的位置,F(·)表示求当前适应度值的函数,LF(·)表示Levy飞行生成的扰动值。

Case 4:累速俯冲式硬围攻。当r<0.5且|E|<0.5时,猎物没有足够的能量逃跑,在突袭捕捉猎物之前哈里斯鹰会进行一次硬围攻。在这次围攻中,哈里斯鹰试图缩小它与猎物的距离,因此按照式(9)～式(11)所示的策略更新:

Z=Y+S·LF(D)

(9)

Y=Xrabbit(t)-|EXrabbit(t)-Xm(t)|

(10)

(11)

3 改进的哈里斯鹰优化算法

通过分析HHO算法可知,HHO也存在开发能力不足、种群多样性下降、容易陷入局部最优等缺点,这是由于算法对搜索空间开发和探索的不平衡造成的。为了提高算法的性能,平衡HHO算法的开发和探索能力,本文提出了一种具有3种改进策略的HHO算法变体,叫做多策略改进的哈里斯鹰优化算法MHHO(Harris Hawk Optimization algorithm using Multi-strategy)。首先,在HHO中引入混沌局部搜索策略,提高算法的开发能力。利用混沌映射的优点,围绕当前个体进行局部搜索,从而找到更好的个体。其次,为了增强种群多样性,提出了精英备选池策略。此外,为了修改进化方向,本文采用了分布估计策略,通过对优势种群信息进行采样,更好地引导种群方向,从而提高算法收敛速度。最后,采用贪婪策略充分保留优势个体,加快收敛速度。

3.1 混沌局部搜索策略

混沌局部搜索策略通过搜索每一个解决方案的附近区域,从而找到更好的解决方案,因此该策略能够有效提高算法的开发能力。另一方面,混沌映射具有随机性和遍历性的特点,所以利用混沌映射能够进一步提高局部搜索策略的有效性。在MHHO中,混沌局部搜索策略只应用于种群的优势种群。混沌局部搜索策略的公式如式(12)所示:

(12)

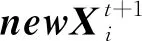
混沌映射的方法有很多种[14],最常见的有Logistic映射、Tent映射和Sin映射。但是,Logistic映射的遍历性较差,对初始参数的设置较敏感,映射点在边缘位置的密度大,在中间位置的密度相对较小,与本文想要达到的种群均衡性的预期不符合。而Tent映射值的分布比较平坦、均匀,映射的均匀性相比于Logistic映射的均匀性更好,能够提高算法的寻优速度。考虑结合完全随机化的特点,MHHO将Tent混沌映射生成Ct,同时在[0,1]产生分布较均匀的初始值。Tent混沌映射分布值如图1所示,Tent映射表达式如式(13)所示:

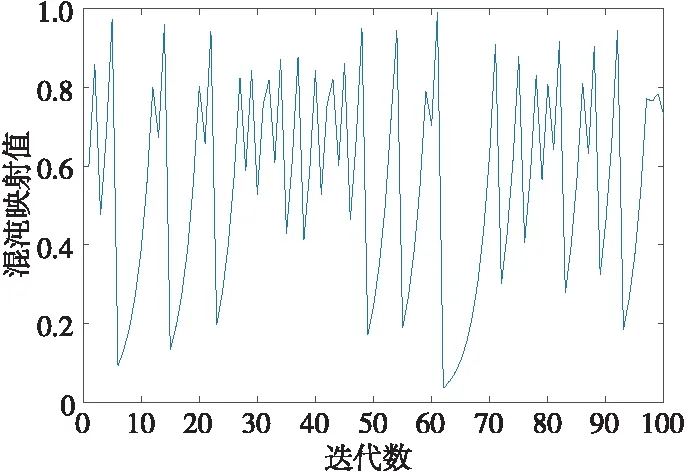
Figure 1 Tent chaos mapping

(13)

3.2 精英备选池策略

在早期迭代阶段,HHO通过跟随最优个体更新其余个体位置信息,虽然这有利于算法加快收敛,但会减弱种群的多样性,容易导致算法陷入局部最优[15]。此外,在迭代后期,使用Levy捕食策略时,同样仅跟随最优个体。为了保证算法开发和探索的平衡,本文提出了一种精英备选池策略,将当前最好的3个个体放入一个集合,如式(14)所示:

Xesp={Xesp1,Xesp2,Xesp3}

(14)

其中,Xesp1、Xesp2和Xesp3是种群中最好的3个个体。

食物源每次都从这3个个体中随机选择。通过使用精英备选池策略,食物源的位置从最优个体变为最好的3个个体中的一个,这在一定程度上避免了因最优个体陷入局部最优而导致算法早熟收敛。为了平衡算法的开发和探索,本文算法还将全局最优个体放入精英备选池,以确保每一个个体有机会向最优个体靠近,确保算法的收敛效率。因此,精英备选池策略的最终数学模型描述如式(15)所示:

Xesp={Xesp1,Xesp2,Xesp3,Xbest}

(15)

避免局部最优一直是群智能算法的一个重大难题。本文通过精英池策略能够有效地避免个体陷入局部最优。最终的精英池由几个最好的个体随机组成,这保留了选择优势个体的可能性,也给当前种群提供了更大的选择范围。由于精英池内的个体是随着每次迭代进行更新的,所以不必担心精英池内的个体陷入局部最优导致整个算法陷入局部最优的情况发生。

为了更直观地比较原始HHO算法与使用精英池策略改进后HHO算法的区别,本文选取CEC2017中F3、F4、F9和F10作为测试函数。

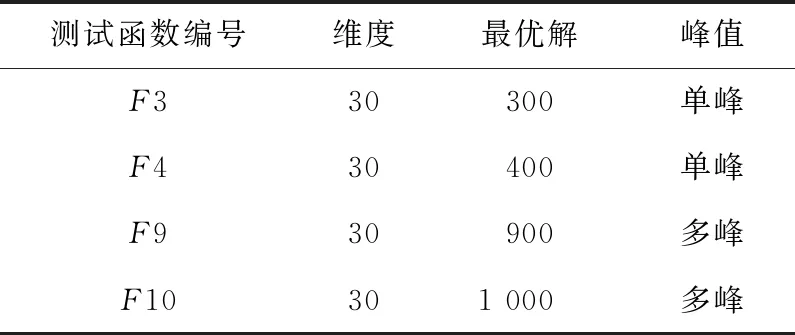
Table 1 Test functions

从图2中可以很明显地看出,在4个测试函数上,精英池HHO算法比原始HHO算法有更好的收敛性和收敛速度。

3.3 分布估计策略

在原始的HHO中,迭代过程中种群的更新主要由迄今为止得到的最佳解引导,因此种群的多样性在算法过程的后期迅速减少,导致HHO很容易陷入局部最优。分布估计策略的核心是加权协方差矩阵,具有较强的局部最优规避能力。因此,本文采用加权极大似然估计法对分布模型进行估计,选取表现较好的前一半作为优势总体,以充分利用有希望的种群信息来估计更好的进化方向。该策略的数学模型描述如下:

(16)

(17)

Cov=

(18)

(19)

(20)

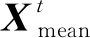
在每一次迭代完成之后,使用贪婪策略保留父代群体和子代群体中的最优NP个个体形成新的群体,这样进一步提高了MHHO算法的全局收敛能力。

3.4 改进算法流程图

MHHO的流程图如图3所示。

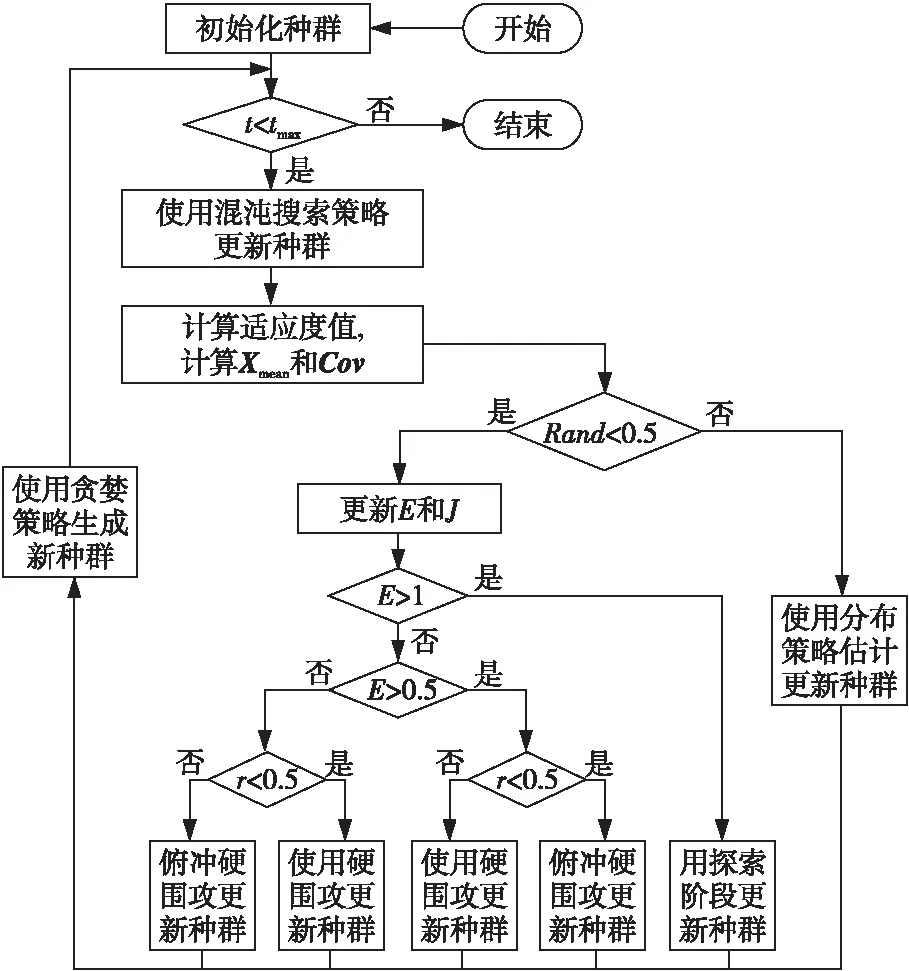
Figure 3 Flow chart of MHHO algorithm

3.5 时间复杂度分析

本节对HHO算法和MHHO算法的时间复杂度进行分析。对于原始的HHO算法而言,种群规模为NP,搜索空间维度为D,最大迭代次数为T,需要优化的目标函数为f(x),由此可知HHO算法的时间复杂度为:O(NP)+O(T·NP·D)+O(T·NP)。

MHHO算法每次只对优秀种群使用分布估计策略产生出M个变异新解。MHHO会计算M+NP/2个个体的适应度值,从得到的适应度值中挑选出前NP/2个个体进入下一轮更新。计算M+NP/2个个体的适应度值的时间复杂度为O(T·(M+(NP/2)))。将这些得到适应度值的个体进行排序的时间复杂度为:O(T·(M+(NP/2))log(M+(NP/2))),所以MHHO算法的总时间复杂度为:O(NP)+O(T·(M+(NP/2)))+O(T·(M+(NP/2))log(M+(NP/2)))+O(T·NP·D)。

4 仿真实验和结果分析

4.1 测试函数和初始化参数

为了充分验证MHHO算法的优越性,本文使用IEEE CEC2017单目标测试函数对算法进行测试。CEC2017测试集由16个测试函数组成。F1是一个只有一个全局最优解的单峰函数,用来验证算法的局部搜索能力。F2～F4是多峰函数,主要用于测试算法跳出局部最优的能力。F9～F12、F17和F18是混合函数,F19、F20、F25～F28是复合函数,可以用来测试算法在现实世界中解决复杂优化问题的潜力。表2给出了函数及其全局最优点。

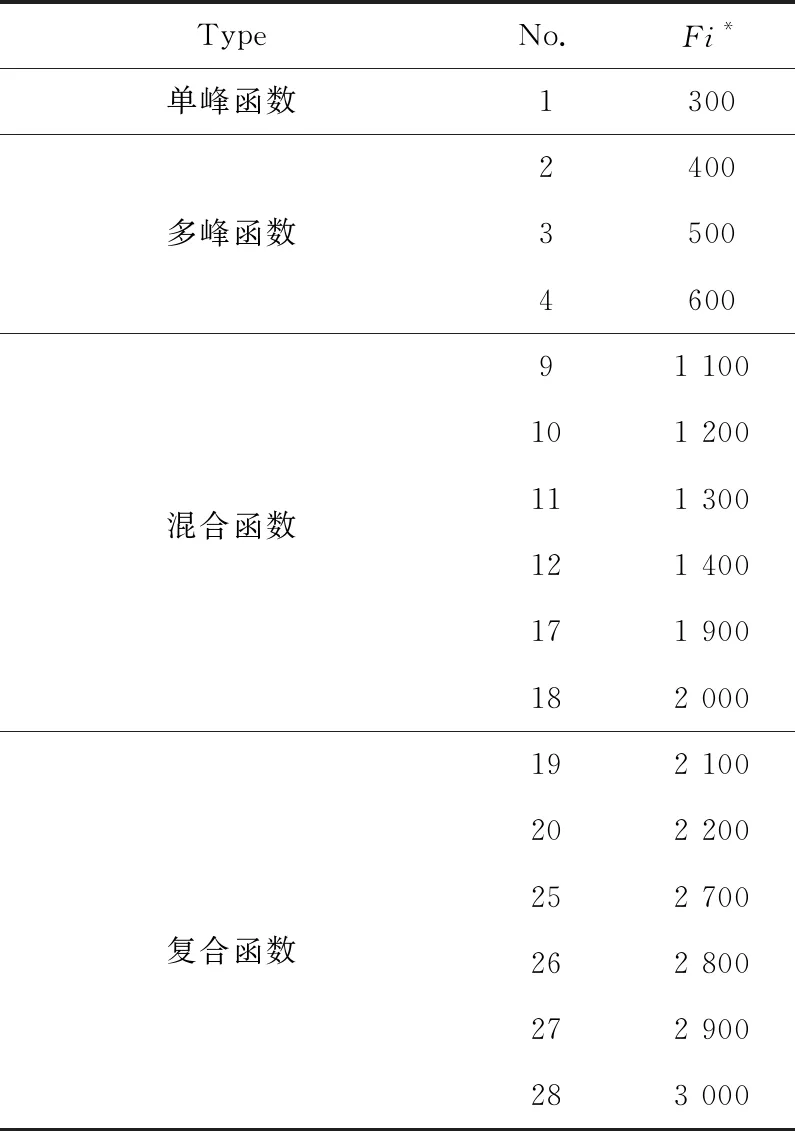
Table 2 CEC2017 test functions

为了保证公平性,对于经典测试函数,所有算法都采用相同的维度,最大迭代次数设置为300,种群数量设置为50,分别对每个函数独立求解30次。对于CEC 2017测试集,维度(Dim),最大迭代次数tmax和种群数(NP)分别被统一设置为30,600和500。所有测试函数独立运行51次。本文实验在一台装有Intel i5-8500U处理器和8 GB内存的计算机上进行,并使用Matlab R2020a进行编程。

4.2 实验结果与分析

本节将最近提出的5种算法与MHHO进行比较。这些最先进的算法包括蝴蝶优化算法BOA(Butterfly Optimization Algorithm)、樽海鞘群算法SSA(Salp Swarm Algorithm)、算术优化算法AOA(Arithmetic Optimization Algorithm)、寻路者算法PFA(PathFinder Algorithm)和被囊群算法TSA(Tunicate Swarm Algorithm)[16-20]。所有算法的参数设置与原文献的一致,如表3所示。

Table 3 Algorithm parameters setting

本文通过数值分析、收敛分析、稳定性分析、Wilcoxon符号秩检验、Friedman检验对MHHO的性能进行全面评估,结果如表4所示。

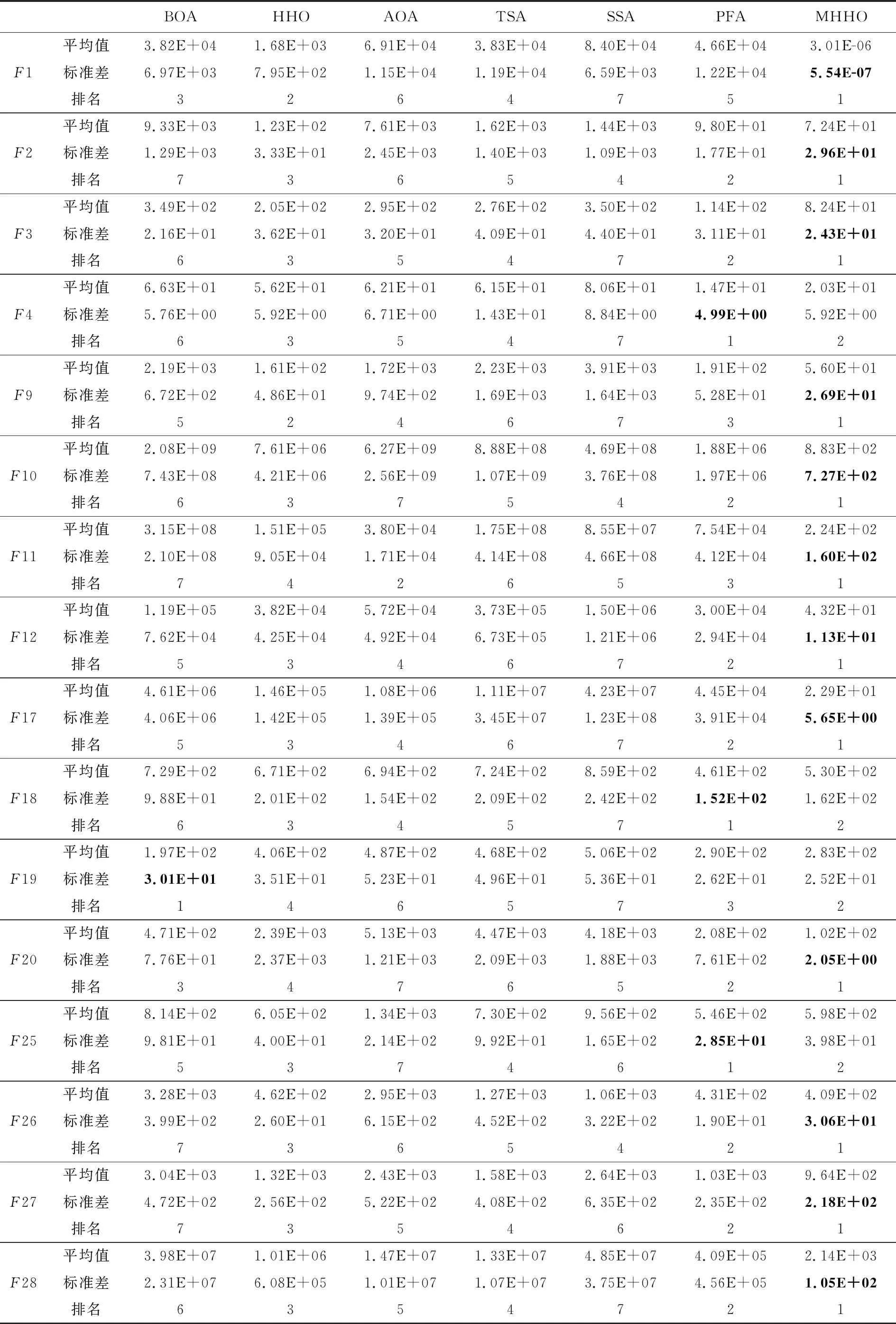
Table 4 Statistical results of seven algorithms on CEC2017 test functions

从表4可知,对于单峰测试函数F1,MHHO性能优于所有对比算法的,虽然MHHO无法取得最优解,但在所有对比算法中表现最好,表明了MHHO具有最强的开发能力;对于多峰测试函数,MHHO在2个测试函数(F2和F3)上表现最好,在F4上PFA取得了最好的结果,MHHO均排在第2位,MHHO在多峰函数上的表现说明改进算法能够保持足够好的种群多样性,避免了陷入局部最优;对于混合函数和复合函数,每个算法各有优劣:MHHO在F9～F12、F17、F20、F26～F28上获得了最优解,PFA则在F18和F25上求得了更好的解,BOA在F19上表现优于其他对比算法的。总的来说,MHHO在复合函数和混合函数上取得的结果均排在前两位,很好地表明了MHHO解决现实世界中复杂优化问题的潜力。值得注意的是,MHHO在所有测试函数上的表现都优于HHO,表明本文提出的改进算法性能更好。

为了分析改进算法所求解的分布特性,根据各算法51次独立求解的结果绘制了箱式图,如图4所示。对于每种算法,每个框的中心标记表示51次求解函数结果的中位数,框的底部和顶部边缘表示一等分点和三等分点,符号“+”表示不在箱子内的坏值。从图4可以得知,在求解其中5个测试函数(F3、F12、F20、F27和F28)时,MHHO没有异常值,这表明MHHO所求解的分布非常集中;同时,对于其它在箱式图中存在异常值的测试函数(F1、F2、F9～F11、F17、F26),MHHO有着最小的中位数,表明MHHO的解的质量相对更优。因此,本文提出的改进算法具有很强的鲁棒性。

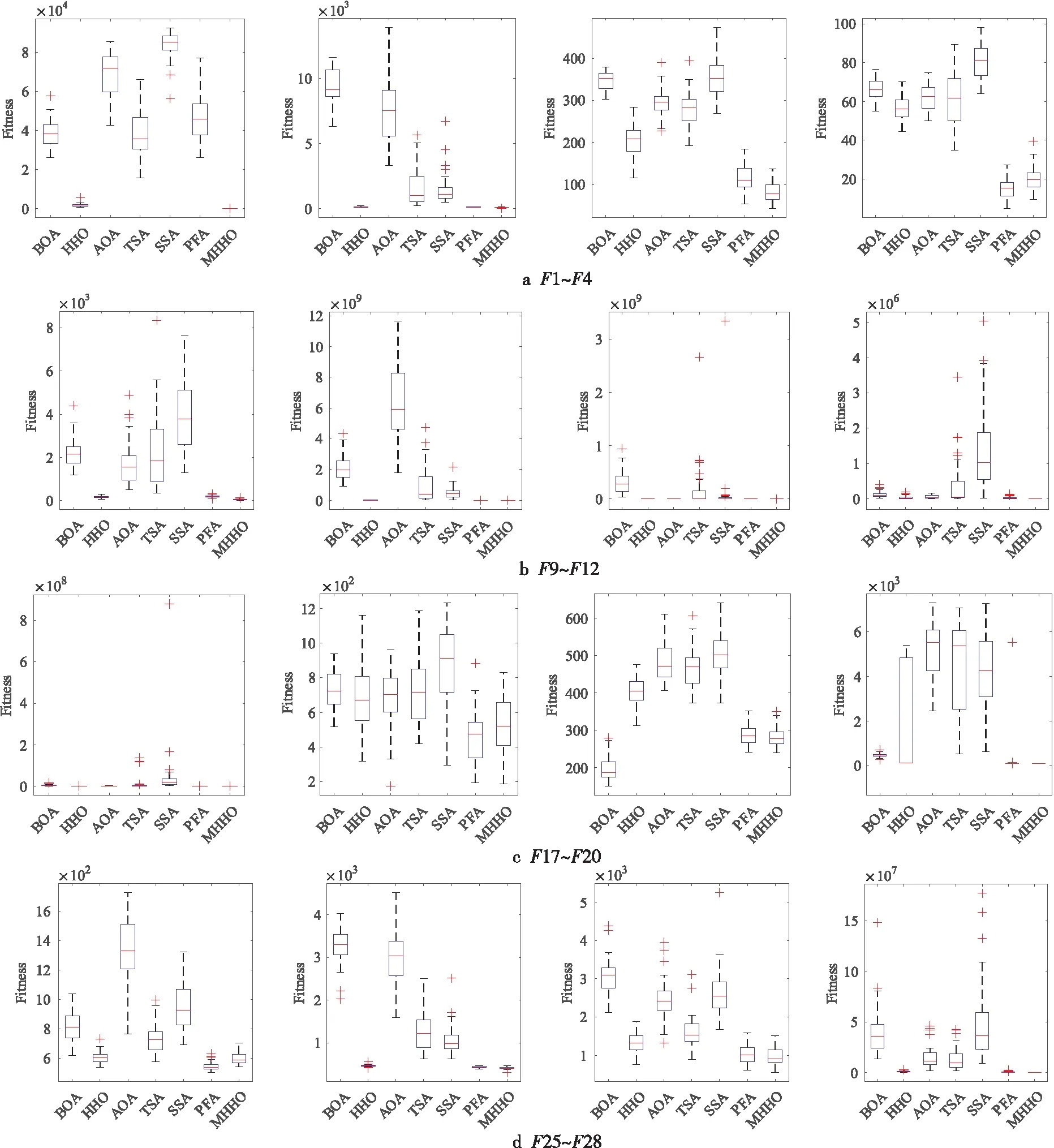
Figure 4 Box diagrams of CEC2017 test functions

为进一步说明算法的收敛性能,将适应度值为以10为底的对数计量的适应值(Fitness)作为每个算法收敛精度的评判标准。图5展示了7种算法求解CEC2017测试集的平均误差收敛曲线图(迭代曲线图),横坐标表示算法的迭代次数,纵坐标表示算法的收敛精度,也就是最终得到的适应度值。结合以上7种算法在每个测试函数所展现出的进化曲线和收敛精度,实验结果分析如下:

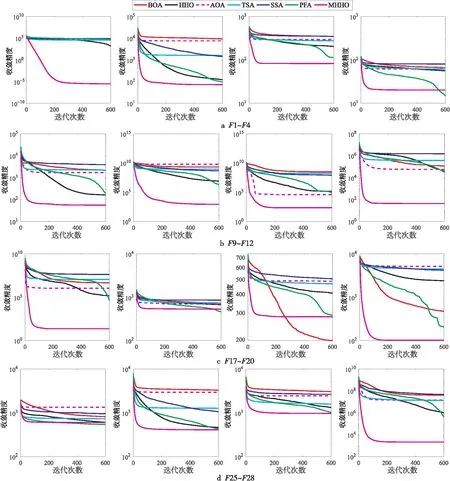
Figure 5 Convergence diagrams of CEC2017 test functions

对于单峰函数F1,MHHO有更好的收敛精度和更快的收敛速度。对于多峰函数F2～F4,MHHO在F2和F3上有更好的收敛精度和更快的收敛速度,PFA则在F4上具有更好的收敛精度。对于复合函数和混合函数,MHHO在求解其中的9个函数(F9～F12、F17、F20、F26～F28)时,收敛速度更快,收敛精度更高。值得注意的是,MHHO在所有测试函数上的寻优精度和收敛速度都比HHO的更好。综上所述,MHHO在收敛精度和收敛速度方面优于对比算法。

为了测试函数的时间消耗(单位为s),本文挑选了CEC2017中几个有代表性的单峰、多峰以及混合函数来对改进策略进行评估。

从表5可以发现,无论是单峰函数、多峰函数还是最复杂的混合函数,MHHO的时间消耗都控制在7 s左右;HHO的时间消耗极度不稳定,且远高于MHHO的,这说明改进算法具有更好的性能。

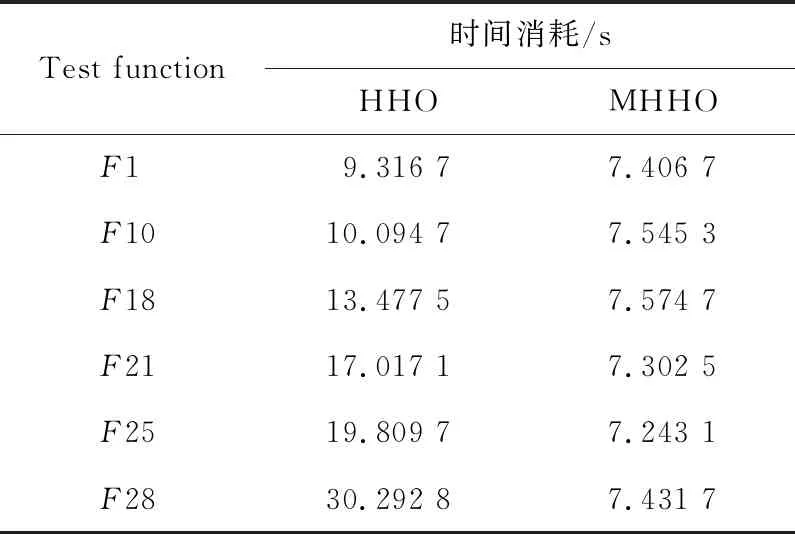
Table 5 Time consumption of two algorithms on test functions

仅根据平均值比较算法性能还不充分,为了避免测试中的偶然性,本文使用Wilcoxon符号秩检验来验证改进算法与对比算法是否在统计上存在显著差异。表6列出了每种算法和MHHO的Wilcoxon符号秩检验的结果。在表6 中,“+”表示MHHO的优化结果优于对比算法的,“-”表示结果较差,“=”表示结果相似;符号“R+”是一个正等级值,表示MHHO比对比算法更好的程度,“R-”表示相反的结果。从表6可以看出,MHHO至少在12个测试函数上优于所有对比算法,并且在所有测试函数(15个)上均优于原始HHO,在统计学上验证了改进算法的出色性能。

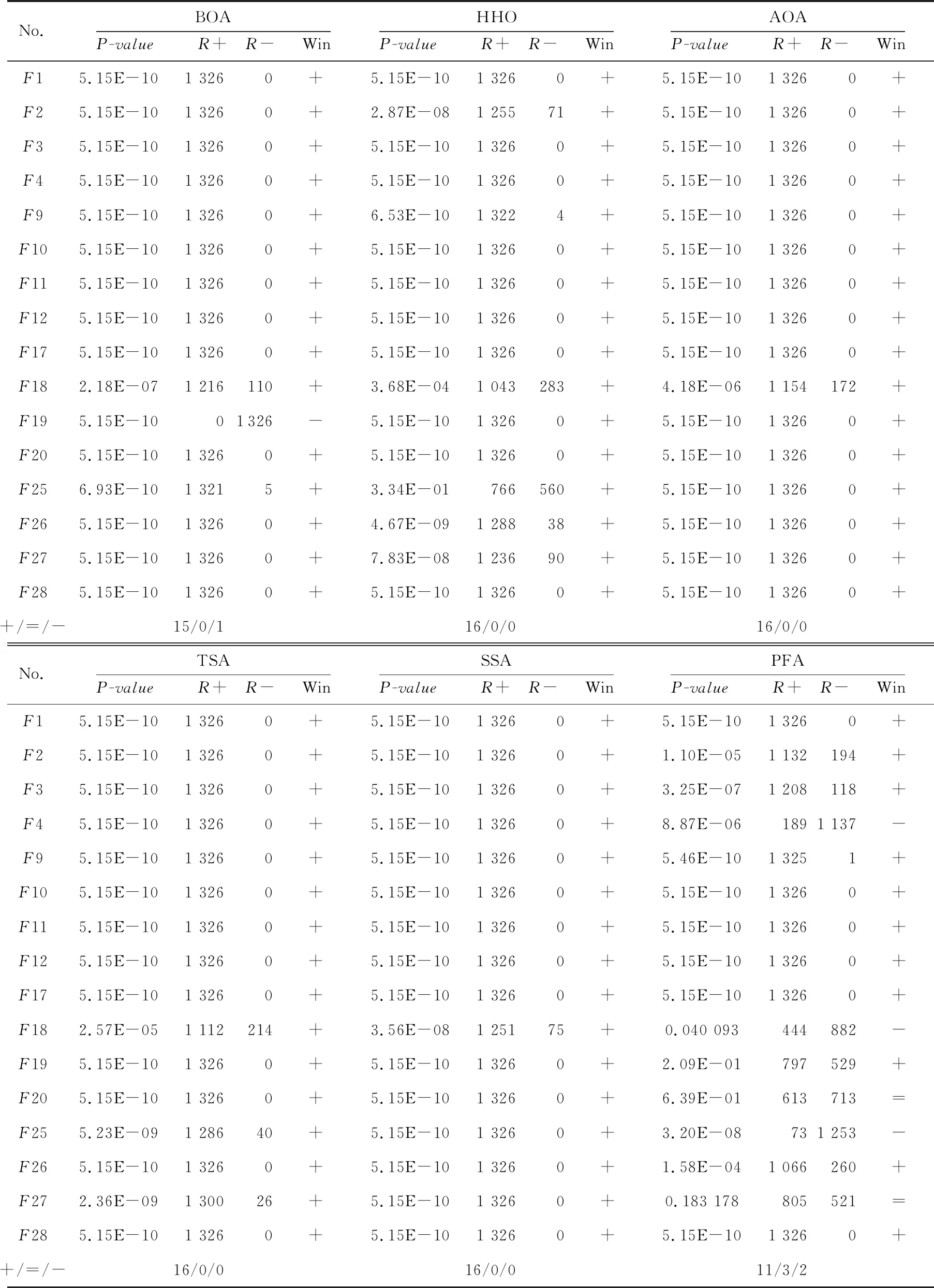
Table 6 Results of Wilcoxon signed rank test

通过CEC2017测试集对MHHO的性能进行验证,实验结果表明:改进策略均能有效提高算法性能;和BOA、AOA、TSA、SSA和PFA相比,MHHO无论是在收敛精度和收敛速度,还是在算法稳定性上,均有显著优势,证明了本文改进算法的优越性。

5 工程约束问题

工程设计问题是一个几何形状复杂、设计变量多、实际工程约束多的非线性优化问题。本文通过求解实际工程问题对MHHO的性能进行评估。考虑到这些工程设计问题都是包含不等式和等式的约束优化问题,利用罚函数将约束优化问题转化为无约束优化问题。这些问题包括压力容器设计问题和拉压弹簧设计问题,均使用相同的迭代次数(500)和种群(200)来解决这些优化设计问题。每个问题独立运行30次,并将统计结果与文献中的其他算法进行比较。

5.1 压力容器设计问题

图6所示的压力容器设计问题是一个典型的混合优化问题,其目标是降低包括成形成本、材料成本和焊接成本在内的总成本。有4个不同的变量:容器厚度Ts(x1)、封头厚度Th(x2)、内径R(x3)和容器圆柱截面长度L(x4)。这个问题的数学描述如式(21)～式(24)所示:

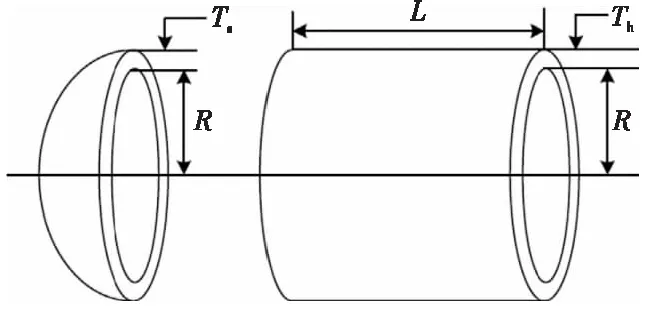
Figure 6 Schematic diagram of pressure vessel design

(21)

g2(X)=-x2+0.00954x3≤0

(22)

(23)

g4(X)=x4-240≤0

(24)

约束条件如式(25)所示:

变量范围:1×0.0625≤x1,

x2≤99×0.0625,10≤x3,x4≤200

(25)

各算法运行结果如表7所示。分析表7中数据可知,MHHO在求解压力容器设计问题时的寻优精度和稳定性是最好的。MHHO得到的最佳方案是[0.778 2,0.384 7,40.321 0,199.981 2],说明MHHO在处理该工程问题时能获得最佳结果。

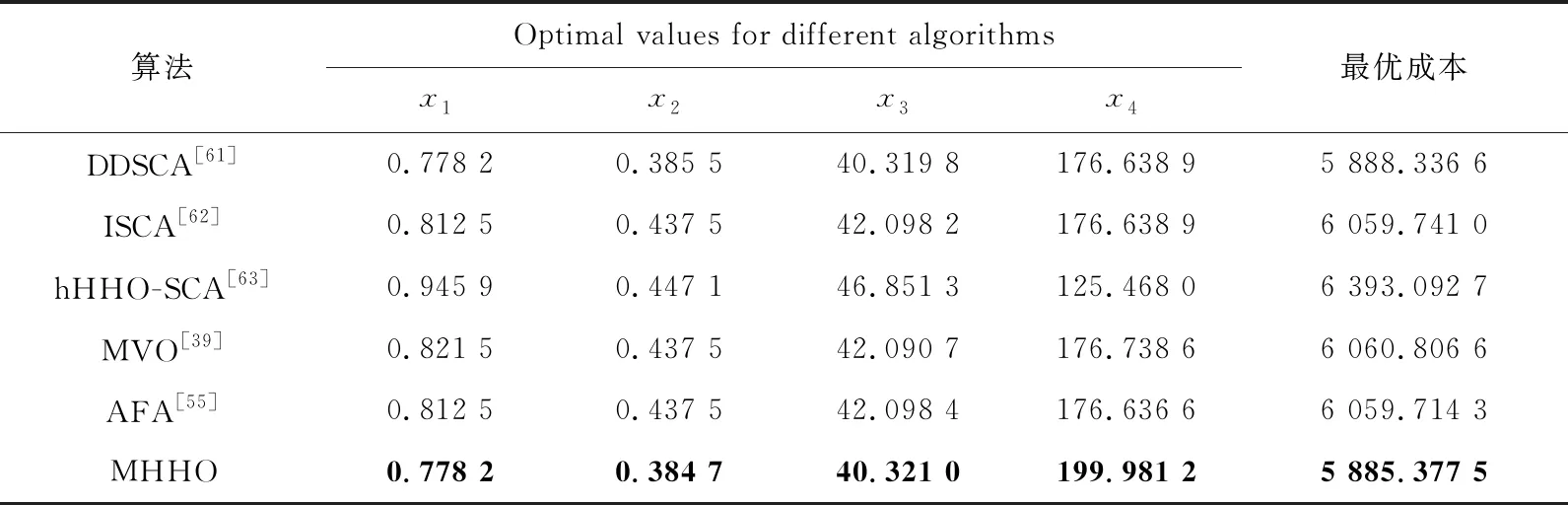
Table 7 Comparison of optimal solutions for pressure vessel design problem

5.2 拉压弹簧设计问题

拉伸/压缩弹簧设计问题是一个机械工程设计优化问题,可以用来评价算法的优越性。如图7所示,此问题的目标是减轻弹簧的重量。它包括4个非线性不等式和3个连续变量:导线直径w(x1)、线圈平均直径d(x2)、线圈长度或数量L(x3)。

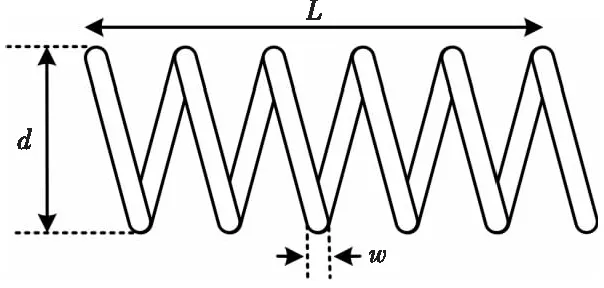
Figure 7 Schematic design of tension spring design

该问题的数学模型可以用式(26)～式(31)所示来描述:

(26)

(27)

(28)

(29)

(30)

约束条件如式(31)所示:

变量范围:0.05≤x1≤2,

0.25≤x2≤1.3,2.0≤x3≤15.0

(31)

各算法运行结果如表8所示。分析可知,MHHO在4项统计数据中均表现最好,说明MHHO具有最好的寻优精度和稳定性,MHHO的最佳方案为[0.051 600,0.354 400,11.424 800]。

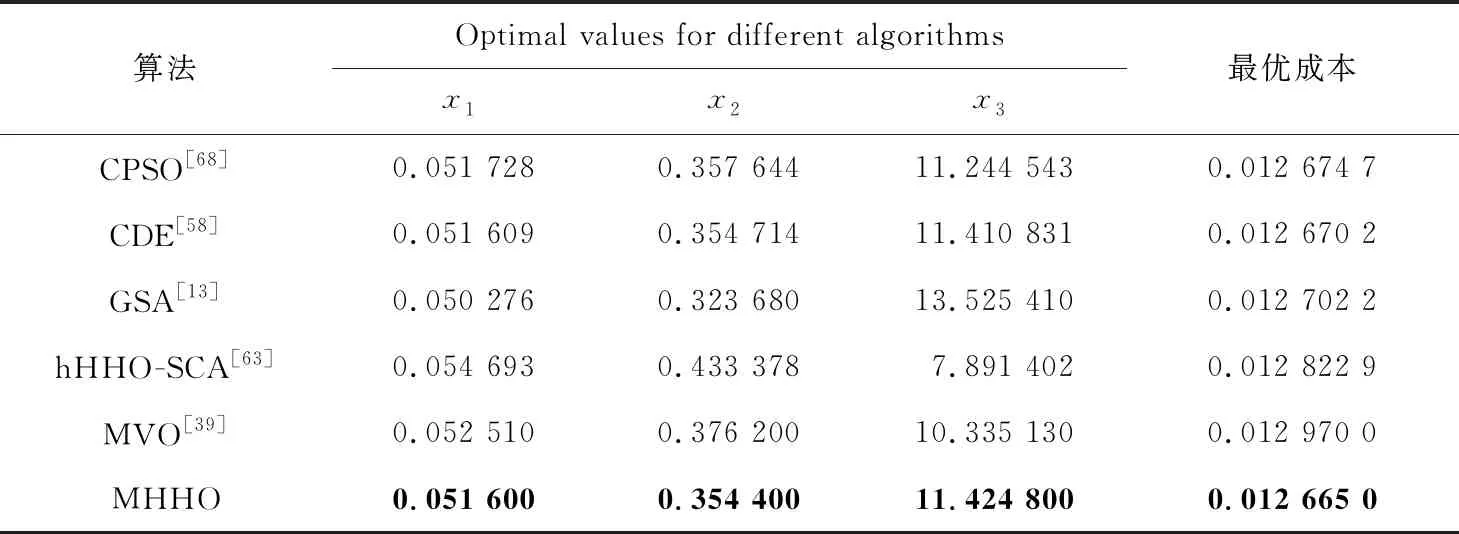
Table 8 Best solution for tension spring design problem

6 结束语

哈里斯鹰优化算法是近几年提出的一种新颖的元启发式算法,其原理简单易懂,算法本身参数较少,易实现,适合与其他的元启发式算法进行结合,也适合解决各种高维问题和多极值问题。本文为了能使算法的性能进一步提升,提出了融合多策略改进的哈里斯鹰优化算法。引入了混沌局部搜索策略,提高了算法的开发效率,围绕单个个体进行扰动,从而找到更好的个体。为了增加种群多样性,提出了精英备选池策略。最后为了修改种群的进化方向,加入了分布式估计策略,能更好地对优质种群进行采样获得其权重值,把种群向更好的方向引导。通过CEC2017测试函数与其他5种新型群智能算法进行比较,实验结果表明,融合了多策略的哈里斯鹰优化算法的性能得到大幅度提高。今后准备把改进后的HHO算法运用到更多的实际工程问题,为解决各种问题提供另一种可行的思路。