吴焕芹, 王茂才,2, 宋志明,2, 陈晓宇,2

1.中国地质大学(武汉) 计算机学院， 湖北武汉 430074；2.中国地质大学(武汉) 智能地学信息处理湖北省重点实验室， 湖北武汉 430074

卫星入轨位置精准度受多种因素的影响,不可避免地存在系统误差和随机误差。系统误差可以在设计或实际操作过程中予以考虑并削减,而随机误差是由偶然因素引起的,难以预测和控制。随机误差亦会导致卫星入轨空间位置的不确定,并在卫星组网和运行过程中传播,对工作效能产生影响。工程实际中对于高价值的重要航天器,一般是通过发动机点火等方式对轨道进行校正和调整,但对于小卫星和微纳卫星,由于其体积小携带有限,进行自身轨道修正的代价较高或远超其设计发射成本,况且大规模星群也没法进行广泛的轨道修正。但不同用途的卫星对位姿精度要求不同,如果能准确快速地估计其位置偏差,可以让工作者做出正确的决策。

当前已经有很多学者对卫星定位精度及运行误差进行了相关研究,并取得了一定成果。如针对卫星的定位精度,Knogl等[1]利用LEO卫星通信信道对GEO卫星进行精确定位。Vighnesam等[2]研究了通过位置差确定IRS运行轨道的系统方法。Zhou等[3]针对北斗卫星定轨提出了一种基于反单点定位的近实时无推力建模方法。Li等[4]实现了利用卫星激光测距分析北斗3号卫星的轨道精度。Larki等[5]研究了基于梯度法确定卫星轨道的方法。白显宗[6]基于历史轨道数据研究了空间目标轨道预报误差与碰撞概率问题。贺若飞等[7]提出一种基于蒙特卡罗卡尔曼滤波的目标定位算法,并应用于无人机目标定位中,取得较好效果。阎海峰等[8]针对伪卫星空中基站位置不易精确确定的问题,建立了组合导航系统和非线性数学模型,提出了一种抗差自适应高斯混合Sigma点粒子滤波算法。文献[9]基于多项式区间参数分析法,针对探测器着陆过程动态特性,提出基于非线性有限元建模的探测器着陆区间分析流程,计算得到探测器着陆动响应上界和下界。文献[10]对分布式InSAR目标三维定位的空间几何关系,给出了定位精度指标与系统参数精度指标之间关系的解析表达式。文献[11]针对三星编队系统,将卫星位置误差源分为体现误差相关性的整体绝对位置误差和体现误差非相关性的星间相对位置误差,从而对存在相关性误差的卫星编队系统进行定位精度分析。在运行误差分析中,文献[12]对影响遥感卫星覆盖的不确定性因素进行归一化量化,对具有不确定性因素影响的指标进行求解,得到具有统计特性的指标结果。文献[13]提出一种线性回归近似替代不确定性,将不确定性参数对于效能影响降维为一个线性组合系数进行求解。文献[14]给出了降维表示方法中功率谱密度函数的解析随机误差,并通过数值算例加以证明。文献[15]提出了一种用神经网络替代不确定性的分析方法,通过人工神经网络在拟合回归分析上的非线性特性,研究分布式卫星系统概念设计中的不确定性参数。文献[16]引入模拟误差场对不确定进行描述,从而获得比较精确的估计数值。

综上可知,目前针对卫星轨道位置精度或误差描述主要有解析法、数值法或通过第三方测量获得;研究对象主要是中、高轨单个高价值卫星或低轨少量卫星系统。相关研究中的解析法是将某时刻卫星位置用轨道根数的解析函数表示,为便于建模学者一般采用简化模型或对不确定性因素做近似处理。该方法在卫星数量不多的情况下适用性较好,但影响计算精度,也不适用于大规模星群。数值法在抽样数量足够多的前提下,可实现对样本的无偏估计,但在卫星规模较大情况下,又存在计算效率低、耗时长等缺点。通过第三方介入测量,又存在过程复杂、成本高等问题。显然上述方法不能满足近几年大量卫星发射入轨,对位置误差多、精、快的评估要求。

本文结合解析法和数值法,采用概率论的知识和误差椭球理论进行研究。首先针对卫星发射入轨位置随机误差,依据卫星入轨六根数不确定性矩阵,利用协方差阵传播率确定地心惯性坐标系下卫星入轨位置在3个坐标轴方向的位置不确定性,构建了描述卫星入轨位置随机误差的一种椭球理论,给出卫星入轨在一定空间范围内的概率计算公式。然后利用STK软件和蒙特卡罗方法,模拟随机因素影响下低轨微纳卫星入轨位置,验证误差理论模型与实际工况的一致性。实验结果表明本文构建的误差椭球理论可以很好地用于估计入轨位置随机误差,尤其是估计大规模星群位置误差,本文方法具有高效性,很好地克服了已有方法的局限性。

1 卫星发射入轨位置表达式

卫星发射入轨位置通常用轨道六根数表示。在航天工程中,卫星六根数期望值根据效能要求精准确定,而卫星实际入轨位置的离散程度通常可通过六根数的不确定性矩阵表示。

1.1 入轨位置不确定性矩阵

假设卫星入轨位置六根数用向量X表示,即:

X=[XaXeXiXEXωXf]T

向量X中Xa,Xe,Xi,XE,Xω,Xf分别表示卫星轨道的半长轴、偏心率、轨道倾角、升交点赤经、近地点幅角和卫星入轨位置的真近点角。

在卫星发射过程中考虑随机因素的影响,其入轨位置为随机变量。设其轨道参数向量X的数学期望为

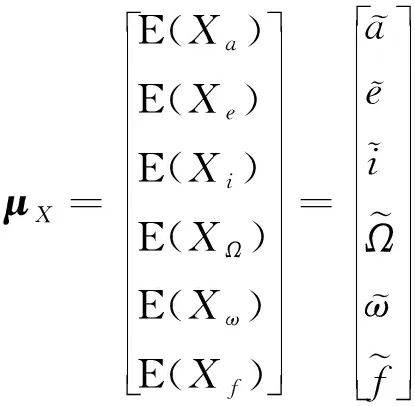
(1)

卫星轨道位置六根数向量X的方差用DXX表示,即

(2)

DXX的主对角线上的元素为轨道六根数随机变量Xa,Xe,Xi,XE,Xω,Xf的方差,非主对角线中的元素是描述2个轨道参数之间相关性的协方差。由于在卫星轨道六根数中,各参数相互独立,即协方差为零,故向量X的方差阵可进一步写为

(3)

由于卫星入轨位置受许多相互独立的随机因素的影响,且每个因素所产生的影响都很小,由中心极限定理,可假设入轨位置六根数服从正态分布。

1.2 卫星入轨位置随机误差表示

图1 卫星入轨点位置误差示意图

(4)

式中,rx,ry,rz为空间位置误差r在x,y,z轴上的分量。显然

(5)

所以

(6)

(7)

2 卫星入轨位置误差模型构建

卫星入轨位置误差σP可以用来评定入轨位置精度,但不能显示在哪个方向上的位差,在讨论卫星或星群的空间碰撞安全、对地覆盖或其他效能时,需要考虑卫星所处轨道位置在哪个方向上的偏差,为此,需要确定卫星在三维空间内的位置矢量差。卫星入轨位置等概率密度点的集合可形成一闭合曲面,该曲面能把各个方向上的误差表示出来(见图2)。但该曲面不是一种典型的曲面,作图也不方便,但其形状与椭球很相似,为便于分析,以椭球近似,称之为等概率密度误差椭球(见图3),简称误差椭球。

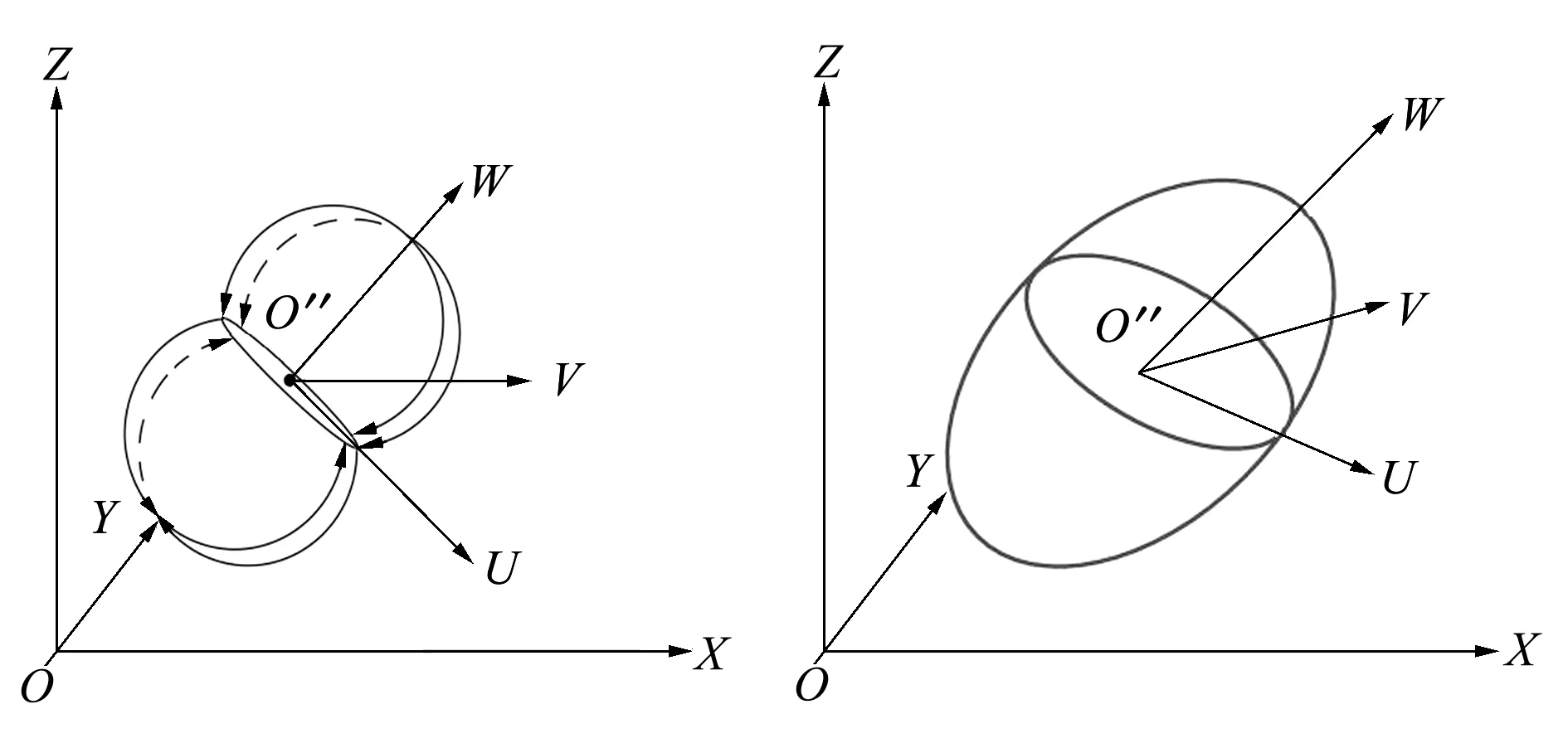
图2 等概率密度点 图3 误差椭球示意图曲面示意图

2.1 误差椭球模型函数

在随机误差下,卫星入轨位置在地心惯性坐标系下呈三维正态分布,其联合分布密度函数为

(8)

式中:Dxx为地心惯性坐标系下卫星入轨位置的不确定性矩阵;|Dxx|为不确定性矩阵的行列式。Dxx的表达式为

(9)

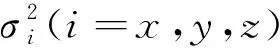
2.2 不确定性矩阵Dxx的确定

已知轨道六根数的协方差阵DXX,根据协方差传播率[17]可以计算不确定性矩阵Dxx

Dxx=ADXXAT

(10)

式中,矩阵A为一个3×6的矩阵,可用(11)式表示。

(11)

2.3 误差椭球轴长的确定

根据联合分布密度函数(8)式,该三维正态分布空间内概率密度相同点的表达式为

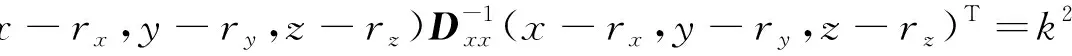
(12)

令x-rx=x′,y-ry=y′,z-rz=z′,则(12)式可写为

(13)

(13)式是地心惯性坐标系下一个相似椭球族表达式,k为放大因子,给定一个k值,就得到一个椭球。为方便分析,进行坐标转换,求出其在主轴坐标系OUVW(如图4所示)内的表达式。

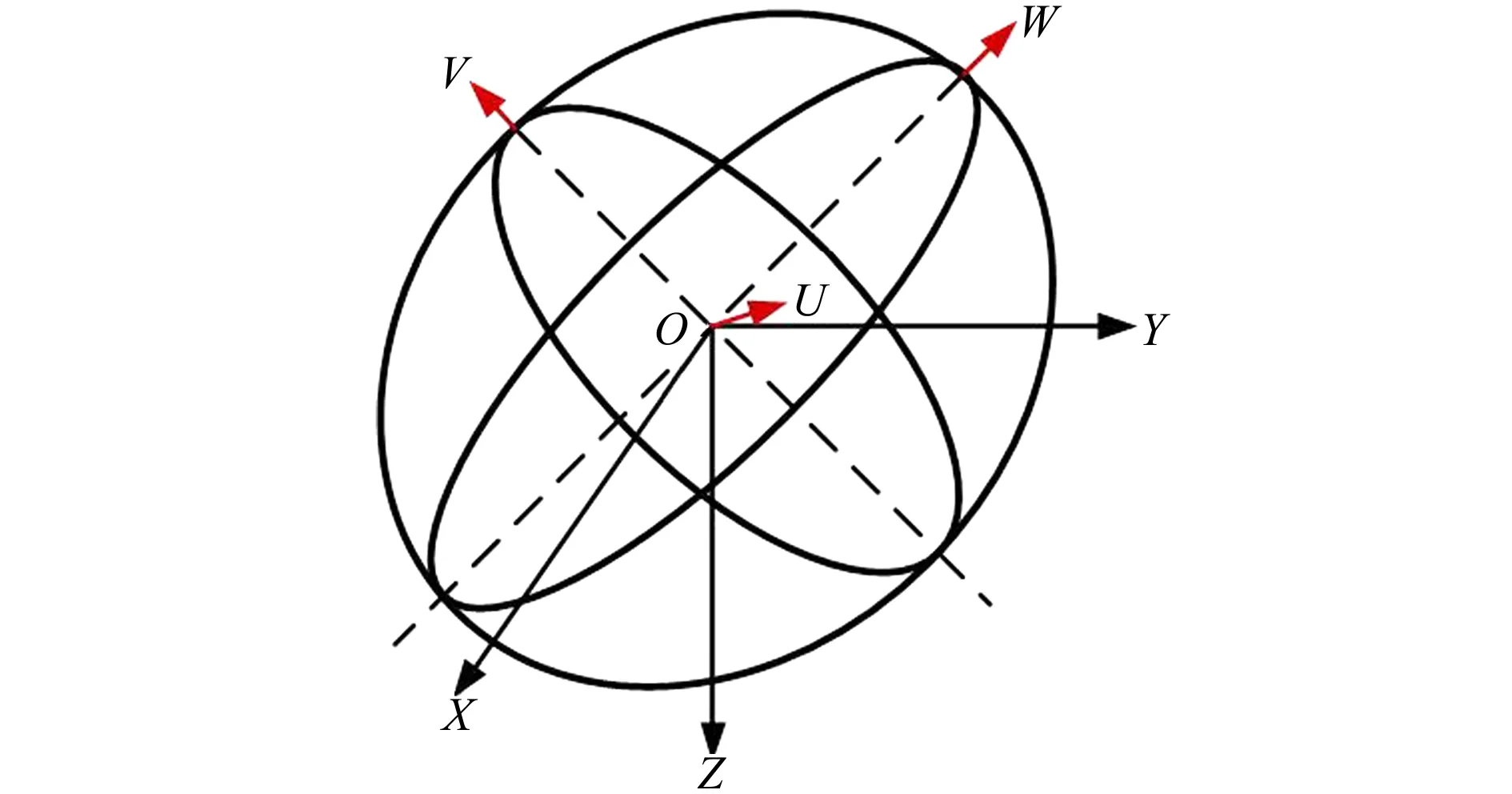
图4 地心坐标与主轴坐标示意图

图4中椭球族的主轴为OU,OV,OW。因为Dxx为实对称矩阵,则存在正交矩阵M,使得

(14)

对(14)式两边同时取逆,得到

(15)

进一步变换形式,得到

(16)

令

(17)

得到

(18)

展开得到

(19)

(19)式为在主轴坐标系下的误差椭球方程,其半轴长平方分别为k2λ1,k2λ2,k2λ3,这里k为前面定义的放大因子,λ1,λ2,λ3为协方差阵Dxx的特征值。已知协方差阵,给定k值,即可确定相应的椭球轴长。

2.4 误差椭球轴向的确定

(14)式中的正交矩阵M=(aij)3×3即是从地心惯性坐标系OXYZ转换到主轴坐标系OUVW的旋转矩阵,由此可以确定椭球3个轴分别与Z轴的夹角。以轴OU为例,如图5所示,OU轴与OZ轴的夹角为α(0°≤α<180°),OU轴在OXY平面的投影与OX轴的夹角为β(0°≤β<360°),由于M为旋转矩阵,则可以直接根据旋转矩阵的元素计算相应角度,并转换到α,β规定的范围内,即

图5 椭球轴与地心惯性坐标轴的夹角示意图

α=arccosa31

(20)

β可由a21,a31通过Matlab中双变量反正切函数确定。

同理,可以计算OV和OW分别与OZ轴的夹角,及其在XOY平面的投影与OX轴的夹角。

3 卫星入轨位置在一定误差范围内的概率

根据概率密度函数(8)式和误差椭球方程(19),卫星入轨在误差椭球内的概率可写为[18]

(21)

令

(22)

代入(21)式得到

(23)

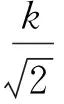
(24)

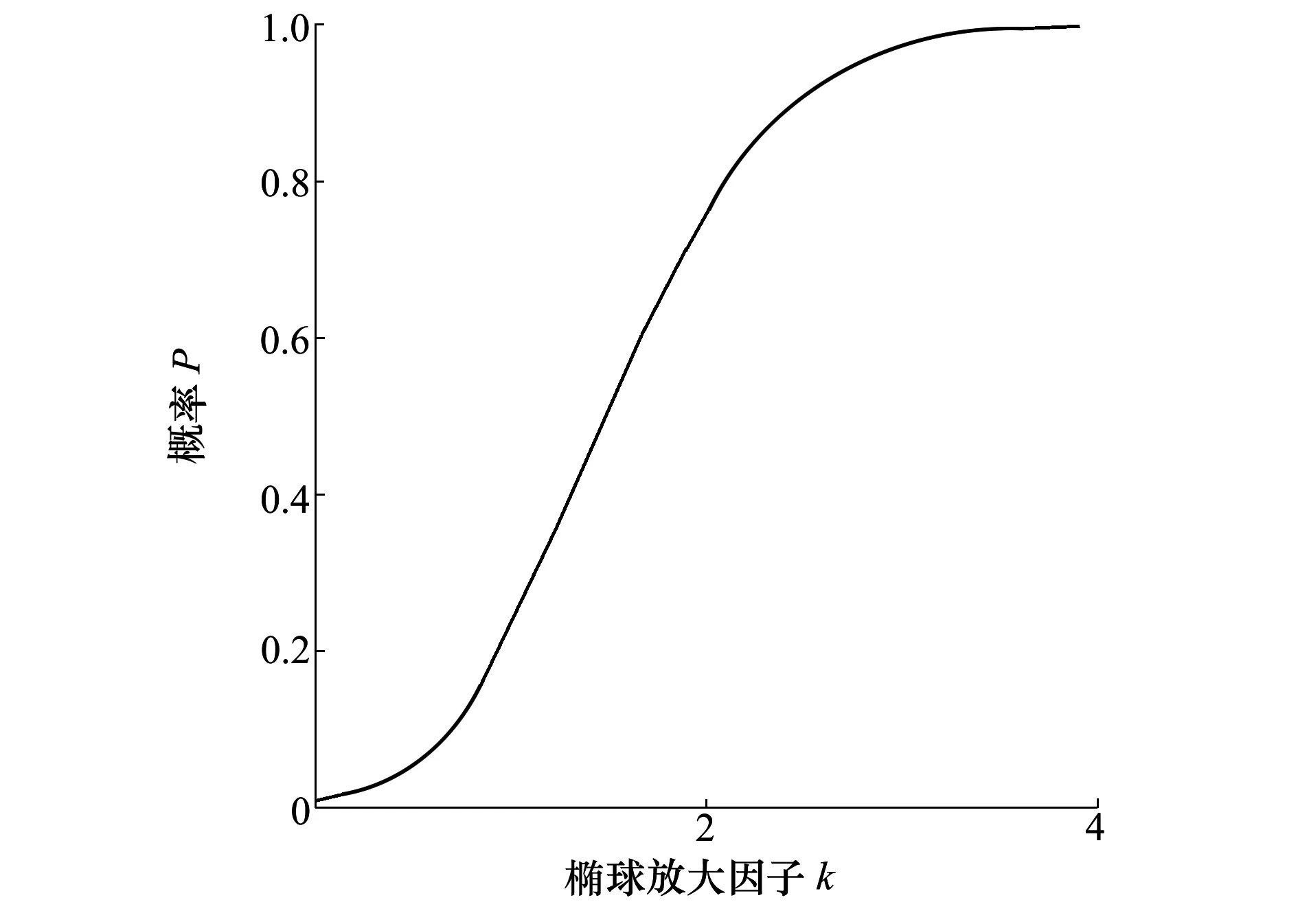
图6 P与k的关系曲线图

从图6可以看出,在随机误差下卫星入轨位置基本都在4倍的椭球轴长范围内。当然,卫星入轨位置在不同的误差范围内的概率亦可得到。

4 算例分析及仿真验证

计划一颗离地526 km的太阳同步圆形轨道卫星发射升空,在真近点角60°入轨,分析其在随机因素影响下卫星入轨位置的随机误差。

4.1 确定相关参数

根据已知要求和给定条件,确定卫星相关参数。

卫星轨道位置采用六根数表示,地球半径按6 378.14 km计算,则其轨道及位置参数如下:

轨道长半轴a=6 904.14 km;轨道偏心率e=0;轨道倾角i=97.5°;轨道近地点幅角ω=0°;轨道升交点赤经Ω=0°;卫星真近点角f=60°。

根据卫星研究所提供的经验数值,依据(3)式确定轨道六根数的协方差阵DXX为

DXX=

(25)

卫星入轨位置在地心惯性坐标系下的位置表达式

(26)

将轨道参数期望值代入(26)式得到地心惯性坐标系下期望入轨位置

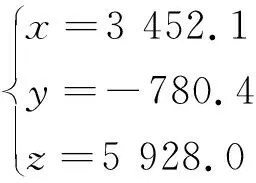
(27)

根据(11)式,对(26)式中x,y,z表达式分别对轨道六根数求偏导,并计算在近似值(期望值)的结果,得到偏导数矩阵A

(28)

根据(10)式得到地心惯性坐标系下的不确定性矩阵

(29)

将Dxx和rx,ry,rz代入(8)式即可得到该卫星入轨位置误差椭球函数。

4.2 误差椭球分析结果

对卫星入轨位置误差椭球函数进行计算,得到正交矩阵M和对应的对角阵

(30)

(31)

据此确定卫星入轨位置误差矢量。当放大因子k取1时计算结果见表1,当k取2.8时(95%的概率落在椭球范围内)误差椭球如图7所示。

表1 椭球分析结果

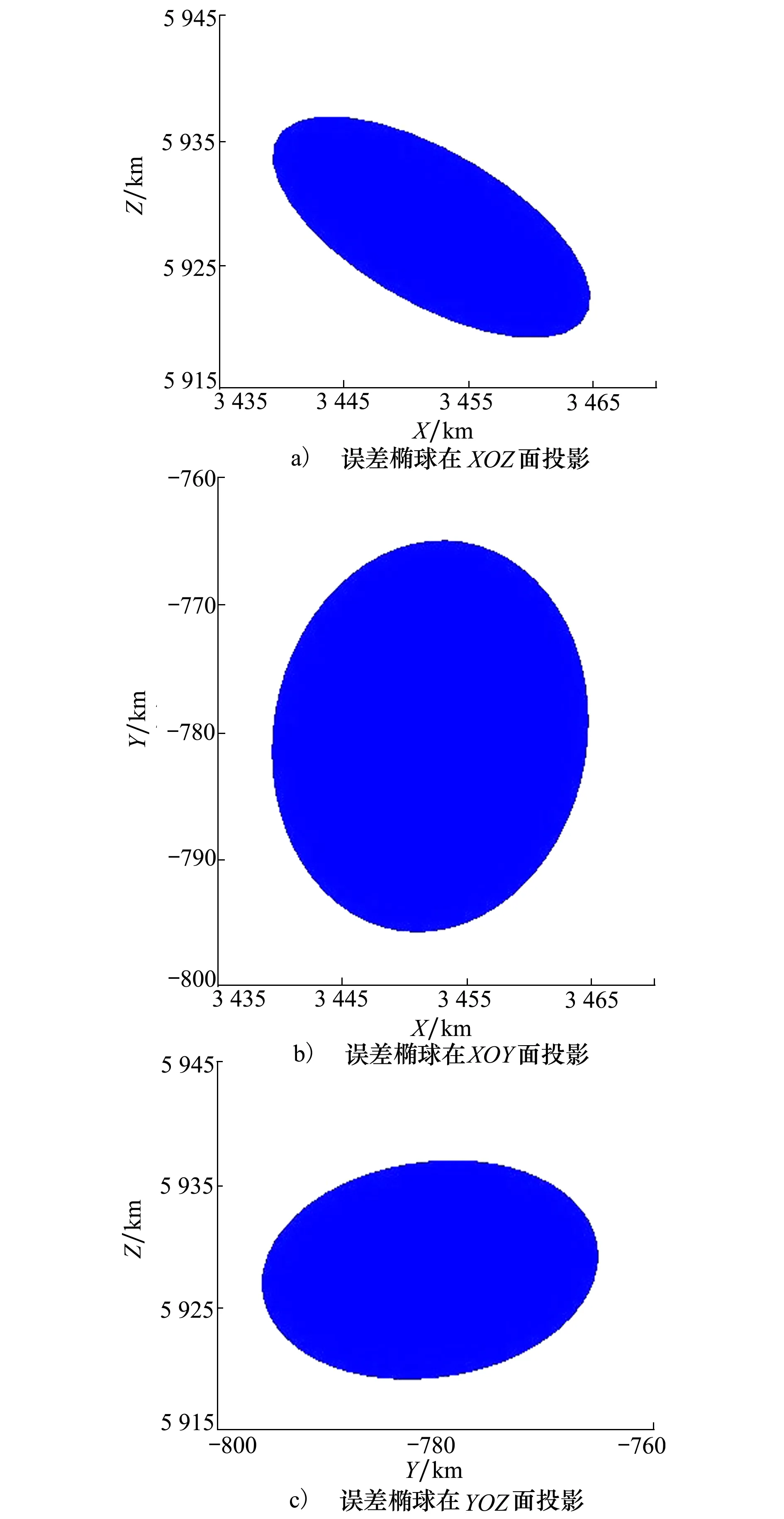
图7 卫星入轨位置椭球仿真结果

进一步地,利用误差椭球理论分析卫星在不同真近点角处的误差椭球、轴长、轴向分别如图8～10所示。

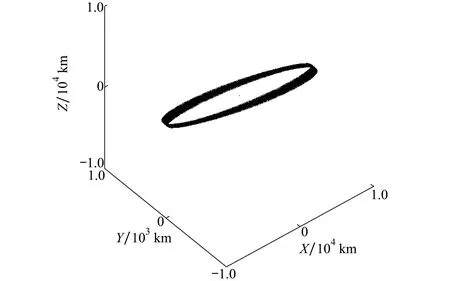
图8 不同真近点角处误差椭球示意图

图9 不同真近点角下误差椭球三根轴长示意图

图10 不同真近点角处误差椭球三根轴轴向示意图

4.3 蒙特卡罗仿真结果

采用同样的轨道六根数协方差阵(15)式,通过STK软件模拟该卫星入轨位置仿真10 000次,则入轨位置分布如图11所示。

图11 蒙特卡罗仿真卫星入轨位置

对10 000次入轨位置求平均值,得到入轨位置x,y,z的平均值(3 452.056 888,-780.432 294 9,5 927.999 303),根据(7)式可得到入轨位置点位方差为15.191 1 km2,入轨位置中误差为3.897 6 km,卫星入轨在一定误差范围内的概率用频度表示,其概率密度直方图如图12所示。

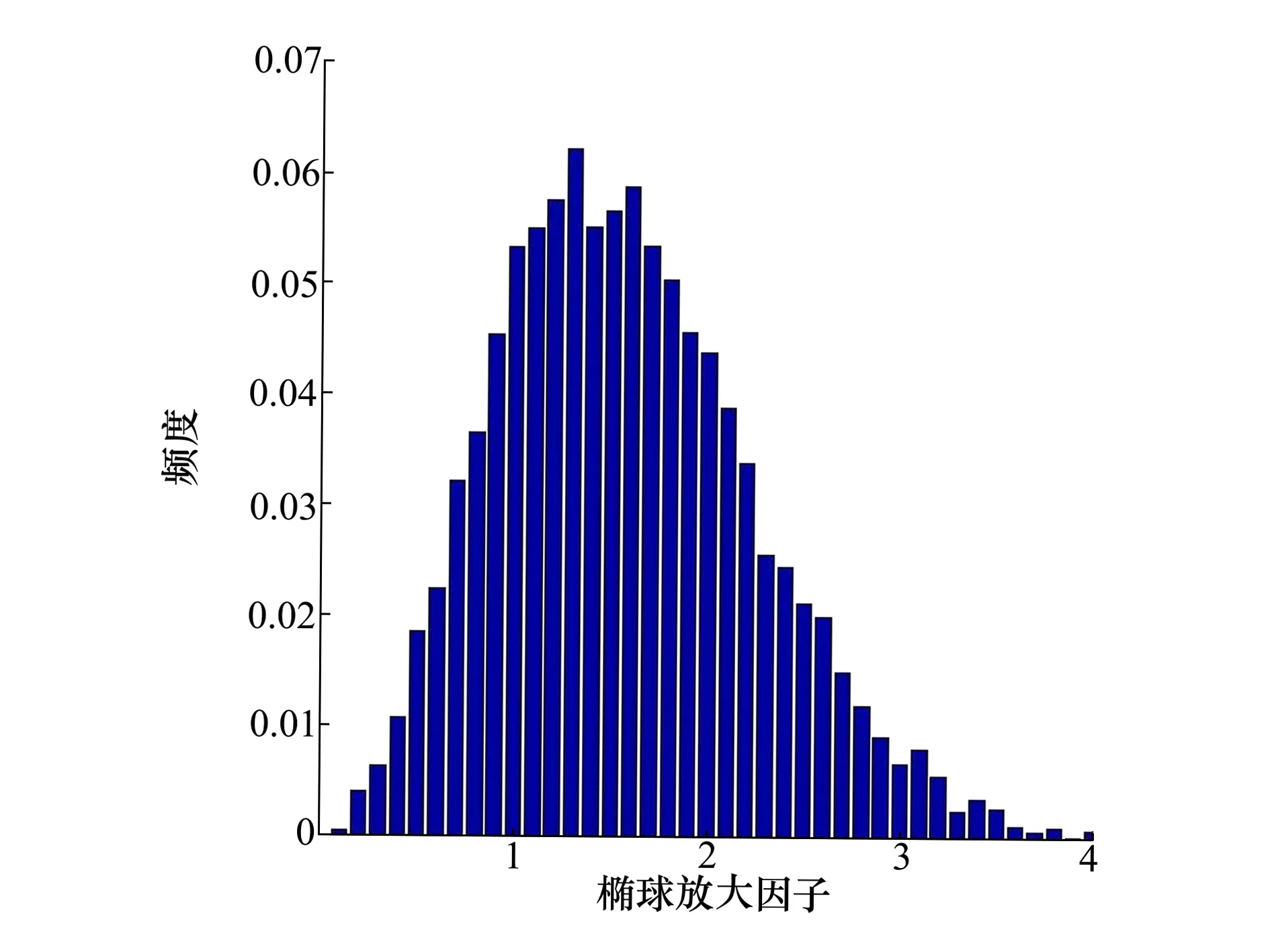
图12 在一定误差范围内出现的概率直方图

对蒙特卡罗仿真结果通过主成分分析,得到卫星分布椭球3个轴长及轴向,如表2所示。

表2 蒙特卡罗结果主成分分析

4.4 2种方法分析结果比较

从表1和表2的结果可以看出,误差椭球分析和蒙特卡罗仿真结果非常接近。

为进一步验证误差椭球理论的合理性,在此采用提出的椭球模型计算卫星落入的概率,并与蒙特卡罗实验仿真方法比较,在特定k值时,2种分析方法呈现的概率结果如表3所示。

表3 卫星落在一定误差范围内的概率

在放大因子k从0～4整个区间,误差椭球理论估算的卫星入轨位置概率和模拟仿真的结果比较,如图13所示。

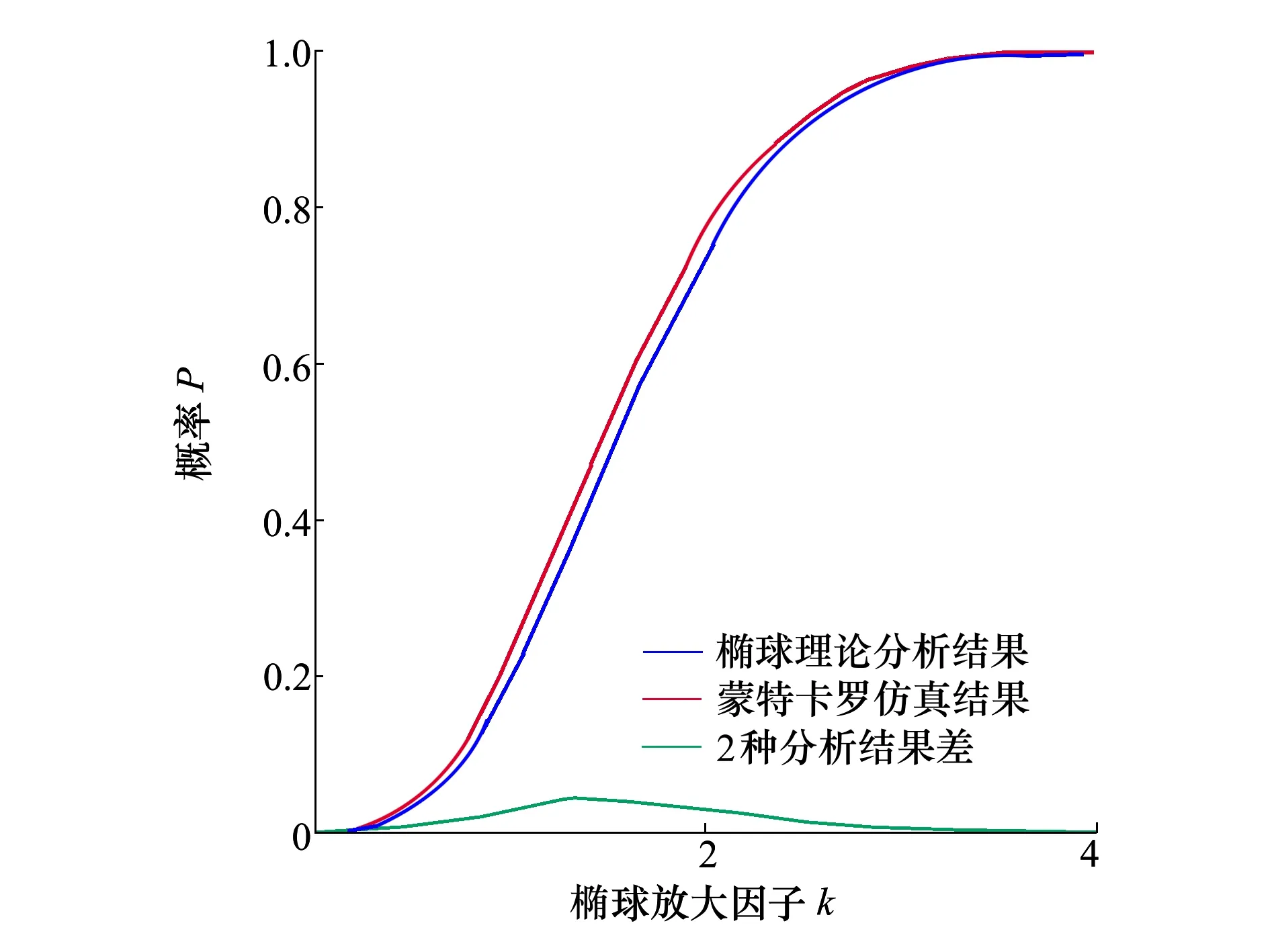
图13 2种方法分析卫星入轨误差概率曲线比较图

从图中可以看出,2个结果非常接近,且误差椭球计算概率略低于蒙特卡罗仿真结果,说明该误差椭球理论模型可以可靠地估计卫星在随机误差下的入轨位置。

5 结 论

本文构建了描述卫星入轨位置随机误差的一种椭球理论模型并验证了其合理性。根据随机误差下入轨位置六根数的不确定性矩阵,把入轨位置随机误差等概率密度曲面近似为椭球,确定椭球三根轴的长度及轴向,并给出卫星入轨在一定误差范围内概率的计算方法。利用蒙特卡罗方法,借助STK软件模拟了一颗低轨微纳卫星在随机因素影响下发射入轨的实验,得到实验卫星入轨位置实际分布,并与误差椭球模型下入轨位置的概率分布对比,结果表明椭球模型分析结果与仿真结果一致,从而说明误差椭球理论可以用于估计入轨位置随机误差,尤其是高效估计大规模星群位置误差,对大规模星群设计及发射具有较好参考价值。

精确地估计卫星入轨位置随机误差,对于计算卫星运行中的碰撞安全、卫星对地覆盖效果等都有很重要的意义,后期可以结合入轨位置误差椭球理论及误差传递特性进一步研究任意时刻卫星运行轨道的误差及对效能的影响。