骆茂森，黄世沛

(温州大学 电气数字化设计技术国家地方联合工程实验室，浙江 温州 325035)

0 引言

随着现代工业、社会经济和计算机技术的快速发展，越来越多的系统和信号需要用多维、多变量的思想来描述。多维系统在数字图像处理、卫星天气云图分析[1]、地震多发区监测数据等方面有着极其重要的应用。这些深厚的工程物理背景使得二维系统 (two dimensional，2-D)的研究方兴未艾，成为控制理论的重要研究领域之一。2-D系统是指状态具有两个独立变量的系统，包括2-D连续系统、2-D离散系统和2-D连续离散系统。2-D连续离散系统包括连续动力学和离散动力学，这两种动力学相互影响。此类系统在实践中有广泛的应用，如长臂采煤[2]、车辆排水[3]、运河灌溉[4]和其他实际工程领域。

在2-D系统的研究过程中发现此类系统容易受到突然变化的影响，此类现象可以用切换系统来描述。切换系统是一种重要的混杂系统，它是由一组动态连续或者是动态离散时间子系统和一条决定子系统之间如何进行切换的切换规则组成[5]。近年来切换2-D系统也引起了国内外学者的广泛关注，且取得了一些初步的成果。例如，文献[6]使用平均驻留时间方法建立了切换2-D离散系统的指数稳定性准则，并设计了状态反馈控制器。文献[7]使用多重Lyapunov函数方法和平均驻留时间方法，建立了切换连续非线性系统的渐近稳定性和指数稳定性准则。文献[8]通过应用模式相关持续驻留时间切换方法，提出了一种适用于切换2-D离散系统的准时间相关滤波方法。文献[9]旨在研究Roesser模型中具有时变时滞的2-D切换正非线性系统的稳定性。文献[10]提出了一类具有多面体不确定参数和脉冲的2-D切换正系统的异步控制问题。

在很多实际控制系统中，执行器饱和是最为普遍的非线性现象之一，这是因为在系统实际运行的过程中，由于执行器元件受到自身物理限制，其输出值往往都是有一定界限的，而不可能趋于无限大。如果不考虑执行器的这一限制就对系统进行设计，会导致系统得不到期望的输出值甚至会酿成重大的事故。近些年，关于具有执行器饱和的2-D系统也引起了越来越多学者的研究，例如文献[11]研究由Fornasini-Marchesini型状态空间方程表示的具有执行器饱和的离散二维切换时滞系统的状态反馈H∞镇定。文献[12]研究了一类控制输入饱和的2-D离散时间切换时滞系统的状态反馈H∞问题。文献[13]介绍了一种通过模糊控制设计来处理具有执行器饱和的二维模糊系统H∞控制问题。文献[14]研究了带有时变延迟和执行器饱和的二维delta算子系统的镇定问题。

需要指出的是，上述关于2-D系统的研究均是基于连续时间控制的，这样的控制策略会使执行器频繁更新，并导致不必要的资源浪费和执行器的损耗。有研究指出事件触发控制[15]既能保持系统的稳定性，还能够弥补传统连续时间控制下造成的有限通信资源浪费的不足。文献[16]研究由Roessor模型描述的2-D离散系统的事件触发控制。文献[17]针对具有干扰的离散2-D Roesser系统，提出了一种事件触发滑模控制(SMC)策略。文献[18]研究了由Fornasini-Marchesini模型描述的2-D系统的事件触发滑模控制问题。文献[19]提出了Fornasini-Marchesini型切换2-D离散系统的事件触发控制方案。然而，到目前为止，具有执行器饱和的切换2-D连续离散系统的事件触发控制问题还未被研究。

基于上述分析，本文将研究具有执行器饱和的切换2-D连续离散系统的事件触发控制问题。为了减少通信资源浪费和执行器的损耗，本文提出了一种用于执行器饱和且含有多参数矩阵的事件触发机制。利用凸组合技术将饱和非线性控制器转化为一组凸包内的线性控制器组合。利用多Lyapunov函数法设计了一种依赖于触发时刻状态的切换信号，并导出了状态反馈控制器存在的充分条件，以保证闭环系统的指数稳定性。

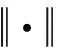
1 预备知识

1.1 基本定义

定义1[20]：考虑以下系统：

(1)

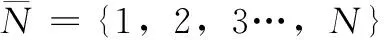
(2)

(3)

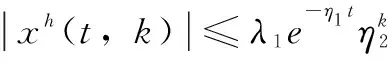
定义2给出系统(1)指数稳定的定义。从定义中可看出，系统要具有指数稳定性，需要满足LV和L∞有界的初始条件。由于系统状态xh(t，k)与xv(t，k)是关于t与k的二元函数，定义2中的指数稳定性质要求系统状态在t与k方向都是指数衰减的。

1.2 基本引理

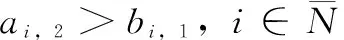
(4)

ΔVi，2(xv)≤-ai，2Vi，2(xv)+bi，2Vi，1(xh)

(5)

则子系统i是指数稳定的。

证明：通过文献[21]中定理3的证明思路，即可得到引理1。

引理1给出了2-D连续-离散系统满足指数稳定性的充分条件，该引理将在下文中用于系统的稳定性证明。值得注意的是，式(4)意味着能量函数Vi，1(xh)在t方向上是输入状态稳定的，其衰减的速率取决于ai，1的大小，式(5)意味着能量函数Vi，2(xv)在k方向上是输入状态稳定的，其衰减的速率取决于ai，2的大小。通过调节ai，1和ai，2的大小可以调节系统衰减的速率。此外，把式(4)和式(5)两式相加，可以得到：

-(ai，1-bi，2)Vi，1(xh)-(ai，2-bi，1)Vi，2(xv)

在上述式子中，divV(x)称为散度。在满足ai，1>bi，2和ai，2>bi，1的前提下，上式可保证2-D连续离散系统是指数稳定的。

1)S<0；

引理2又称为Schur补引理，经常用于矩阵的等价变换，将非线性矩阵不等式转换成可求解的线性矩阵不等式。

引理3[23](状态反馈下的凸组合表示)：给定F∈Rm*n，H∈Rm*n，对于所有状态x∈(H)={x∈Rn：|hsx|≤1，s=1，2m}，有其中hi为矩阵H的第i行，co(·)表示凸包。

引理3在很多文献中都有应用，利用其来处理具有执行器饱和系统线性化的问题，其应用原理是将执行器饱和函数用凸组合的形式来描述，可以将难以处理的饱和执行器转化成可以进行处理的线性化形式。该引理会在下文中用于处理本文研究的切换2-D连续离散系统的执行器饱和问题。

2 问题描述

2.1 系统介绍

本文考虑的具有执行器饱和的切换2-D连续离散系统如下所示：

Bσ(t，k)sat(u(t，k))

(6)

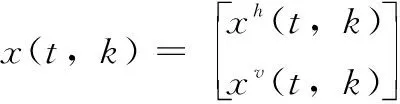
sat(u(t))=[sat(u1(t))，sat(u2(t))，sat(um(t))]T

其中：umax>0表示控制输入的最大幅值。不失一般性，本文取umax=1。

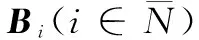
Ai，11∈Rn1×n1，Ai，12∈Rn1×n2，Ai，21∈Rn2×n1，

Ai，22∈Rn2×n2，Bi，1∈Rn1×m和Bi，2∈Rn2×m

系统(6)包含水平状态和垂直状态，它们都是关于t与k的二元函数，有两个维度，且一个维度是连续变量，另一个维度是离散的变量，这与通常的一维(1-D)系统是不同的。进一步地，系统中又有切换信号的存在，并且考虑了在实际中可能会出现的执行器饱和的状况，所以系统(6)被称为具有执行器饱和的切换2-D连续离散系统，该系统是一类重要的混杂系统，关于它在实际工程领域中的应用在引言中已做介绍。Roesser模型是常见的2-D系统模型，本文主要针对切换2-D连续离散Roesser模型展开讨论。由于系统的复杂结构，以及执行器饱和的存在，该系统的稳定性分析与控制器设计具有一定的困难。如引言中所述，事件触发控制既能保持系统的稳定性，还能够弥补传统连续时间控制下造成的有限通信资源浪费的不足，而该问题还未被研究。因此，本文主要讨论该模型在执行器饱和状态下的指数稳定性和事件触发控制器设计问题。

2.2 事件触发条件的选取

对于系统(6)，采用传统的时间触发方案来确定在每一个时刻的传输系统状态可能会导致执行器的损耗和通信通道的冗余。其次，为了充分利用执行器饱和的性质，进一步节约资源，本文设计了一种考虑到饱和特性的事件触发控制方案。

首先设系统上一时刻的传输状态为xh(tg，kl)，xv(tg，kl)(g，l∈)，那么，只有当以下条件满足时才能传输当前状态：

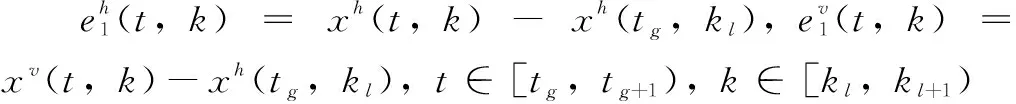
其次，考虑到执行器饱和的性质，定义即将到来的水平瞬时tg+1和垂直瞬间kl+1如下：

tg + 1=tg+ minτ{τ=t-tg|e1hT(t，k)φσ(t，k)he1h(t，k)≥

δσ(t，k)(∂xhT(t，k)φσ(t，k)hxh(t，k)+

(1-∂)xhT(tg，kl)φσ(t，k)hxh(tg，kl))} ∧

{sat(u(t))-u(t)= 0}

(7)

kl + 1=kl+ minθ{τ=k-kl|e1vT(t，k)φσ(t，k)ve1v(t，k)≥

δσ(t，k)(∂xvT(t，k)φσ(t，k)vxv(t，k)+

(1-∂)xvT(tg，kl)φσ(t，k)vxv(tg，kl))} ∧

{sat(u(t))-u(t)= 0}

(8)

其中：∂∈[0，1]。

值得指出的是，式(7)和(8)中的事件触发条件是借鉴了文献[24]中给出的关于2-D离散系统的一个事件触发条件，与之类似的是，所有的传输状态都是整个系统传输序列(xh(t，k)，xv(t，k))的一部分，这种处理使得事件触发控制在原有的基础上更加减少了信号的传输，使得同时在通信通道进行传输的信号量大大减少，进一步节约了通信资源以及减少了执行器的损耗。

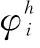
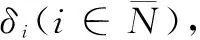
在判断事件触发条件的基础上，当执行器达到饱和状态时，如果满足了事件触发的条件，本应该有一次新的触发，然而此时得到的作用于下一个时间区间的控制量仍然是上一时刻饱和状态的值。因此，在构造事件触发方案时考虑了饱和特性的条件{sat(u(t))-u(t)=0}，只有当执行器处在未饱和状态，且满足事件触发的条件时，才可以进行新的触发，对系统进行这样的处理可以在事件触发的基础上进一步减少触发的次数，从而减少执行器的损耗和通信资源的浪费。

2.3 控制器的设计

在设计的事件触发机制下，状态反馈控制器可以设计为：

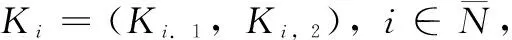
本文使用的事件触发控制方案不同于传统的时间触发控制方案，本小节中设计的控制器是使用状态xh(tg，kl)和xv(tg，kl)这意味着系统控制输入只在触发时刻更新，这既可以降低控制器与执行器之间的通信频率，又可以减轻执行器的磨损。

图1给出了在事件触发控制下的闭环系统的结构图，其中u(t，k)作为执行器的输入，sat(u(t，k))作为执行器的饱和输出。触发条件满足时，事件发生器将当前时刻的状态量xh(tg，kl)与xv(tg，kl)传输至状态反馈控制器，由于零阶保持器的作用，在两个连续的事件发生的区间t∈[tg，tg+1)与k∈[kl，kl+1)内，控制器将沿用上一个触发时刻的状态量，从而可以降低通信通道的拥堵和减少资源的浪费。

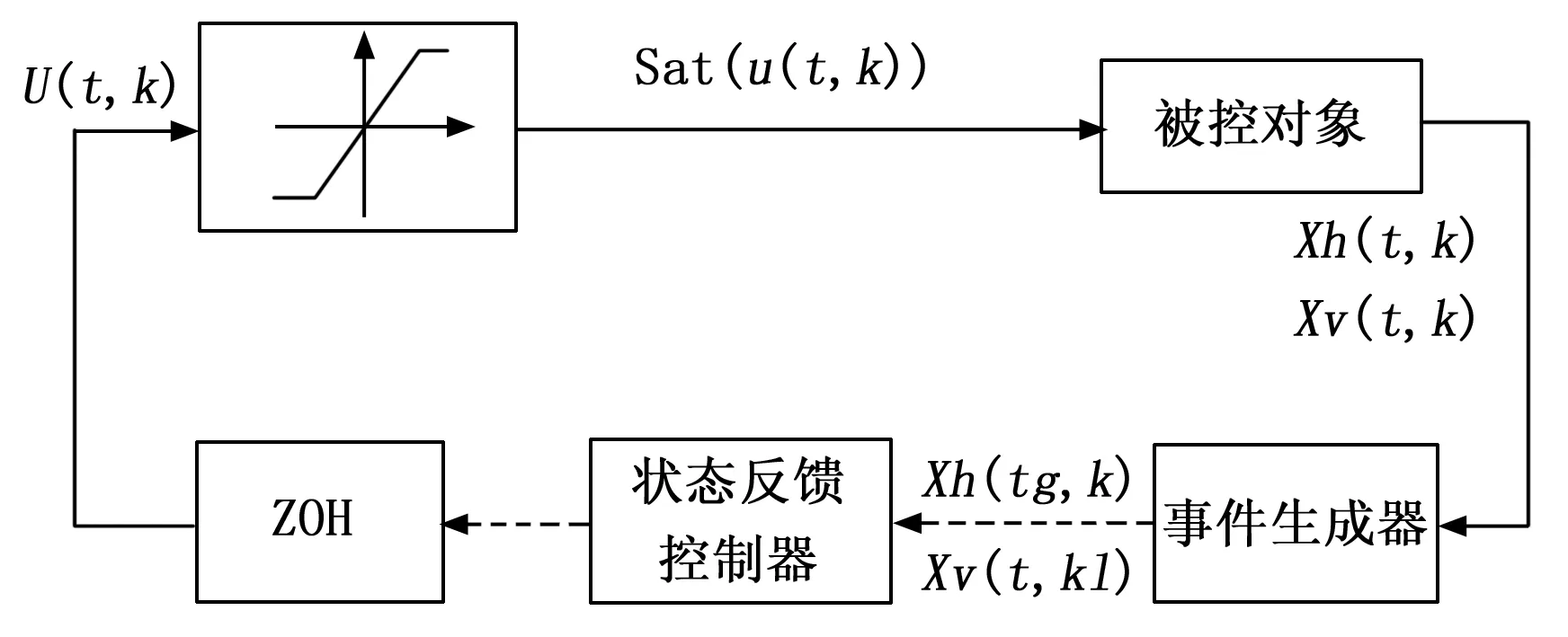
图1 事件触发控制下的闭环系统结构图

对于一个正定矩阵P∈Rn×n和一个标量δ>0，定义椭球体Ω(P，δ)如下：

Ω(P，δ)={x(t，k)∈Rn：x(t，k)TPx(t，k)≤δ}

当x(t，k)∈L(Hσ(t，k))时，根据引理3就可以得出：

(9)

结合系统(6)和状态反馈控制器，在t∈[tg，tg+1)，k∈[kl，kl+1)内，将(9)代入系统(6)，由引理3可以得到如下系统：

(10)

本文利用状态反馈下的凸组合表示方法处理了系统方程出现执行器饱和的情况，将系统(6)表示成系统(10)，使得接下来的处理就与执行器没有发生饱和时的系统的处理方法一致。

3 主要结果

3.1 稳定性分析

在本小节中，我们首先考虑系统(10)的稳定性，以下定理给出了系统(10)指数稳定的一个充分条件。

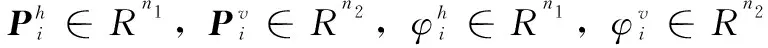
(11)

(12)

(13)

其中：

Hi=(Hi，1，Hi，2)，

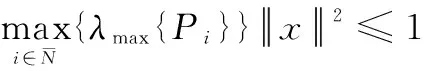
(14)

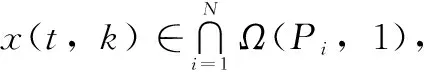
构造如下的Lyapunov函数：

V(t，k)=V1(t，k)+V2(t，k)

其中：

假设在t∈[tg，tg+1)，k∈[kl，kl+1)时，子系统i被激活，i.e.，σ(t，k)=i。

当t∈[tg，tg+1)时，对Vi，1(t，k)沿着系统方程的轨迹对时间t进行求导可得：

上述式子可以写成如下的矩阵形式：

φ(t，k)TΩi，1φ(t，k)

(15)

其中：

当k∈[kl，kl+1)时，对Vi，2(t，k)沿着系统方程的轨迹对时间k进行求差分可得：

ΔVi，2(t，k)+ai，2Vi，2(t，k)-bi，2Vi，1(t，k)=

Vi，2(t，k+1)-Vi，2(t，k)+ai，2Vi，2(t，k)-bi，2Vi，1(t，k)=

同样的，上述式子可以表示成如下的矩阵形式：

ΔVi，2(t，k)+ai，2Vi，2(t，k)-bi，2Vi，1(t，k)=

φ(t，k)TΩi，2φ(t，k)

(16)

其中：

加入事件触发条件之后，我们可以得到：

ϖ(t，k)TΩi，1ϖ(t，k)-e1hT(t，k)φσ(t，k)he1h(t，k)+

δσ(t，k)(∂xhT(t，k)φσ(t，k)hxh(t，k)+

(1-∂)xhT(tg，k)φσ(t，k)hxh(tg，k))-

e1vT(t，k)φσ(t，k)ve1v(t，k)+

δσ(t，k)(∂xvT(t，k)φσ(t，k)vxv(t，k)+

(1-∂)xvT(t，kl)φσ(t，k)vxv(t，kl))=

(17)

ΔVi，2(t，k)+ai，2Vi，2(t，k)-bi，2Vi，1(t，k)≤

ϖ(t，k)TΩi，2ϖ(t，k)-e1hT(t，k)φσ(t，k)he1h(t，k)+

δσ(t，k)(∂xhT(t，k)φσ(t，k)hxh(t，k)+

(1-∂)xhT(tg，k)φσ(t，k)hxh(tg，k))-

e1vT(t，k)φσ(t，k)ve1v(t，k)+

δσ(t，k)(∂xvT(t，k)φσ(t，k)vxv(t，k)+

(1-∂)xvT(t，kl)φσ(t，k)vxv(t，kl))=

(18)

其中：

(19)

(20)

ΔVi，2(xv)≤-ai，2Vi，2(xv)+bi，2Vi，1(xh)

即可通过引理1得到子系统在事件触发条件式(7)和(8)的前提下是指数稳定的。

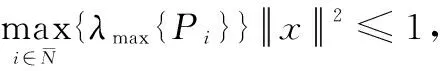
(13)给出了只有在(13)所示的这个收敛域中，才可以利用引理3对系统饱和执行器部分利用凸组合的形式进行处理。不等式(11)和(12)保证了系统(10)满足引理1中条件(4)与(5)，即系统(10)的第i个子系统是指数稳定的。(14)给出了系统切换信号满足的条件，它表明了切换发生在能量函数的最低处，保证了在切换时刻系统的能量函数是非增的，从而使得整个系统的能量函数是递减的，以保证整个切换2-D系统的稳定性。(14)也表明了切换系统只发生在触发时刻，可减少切换频率，从而进一步减少切换发生所需要的资源。

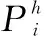
3.2 事件触发控制器的设计

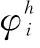
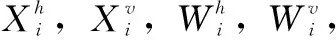
(21)

(22)

(23)

其中：

那么闭环系统在事件触发条件(7)和(8)，如下的切换信号：

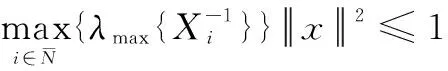
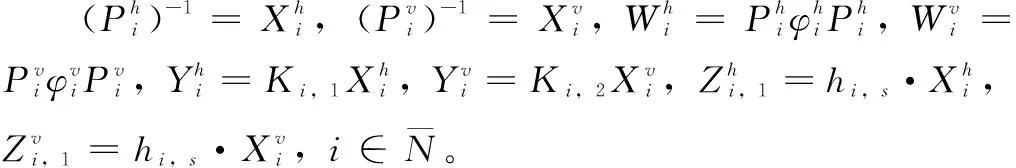
本文提出了具有执行器饱和的切换2-D连续离散系统的事件触发控制器设计方案。与连续时间控制方案相比，该方案能够减少通信资源浪费和执行器的损耗。尽管已有相关文献研究了2-D系统的事件触发控制，但是这些文献都只是针对2-D离散系统，并且未涉及执行器饱和的情况。而本文所考虑的切换2-D连续离散同时具有连续动态与离散动态，还考虑了执行器饱和，其动态行为相比于2-D离散系统来说更加复杂，稳定性分析与控制器设计更加困难。为此，本文采用凸组合技术与多Lyapunov函数法提出了一种用于执行器饱和的切换2-D连续离散系统的事件触发控制方案。该方案包含了事件触发条件、状态反馈控制器与状态依赖的切换信号的设计，且事件触发条件更一般，不仅能保证闭环系统的指数稳定性，还能进一步减少数据传输次数与切换频率。

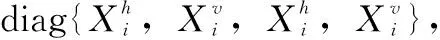
步骤1：给定系统参数矩阵和参数δi，∂，ai，1，ai，2，bi，1，bi，2。

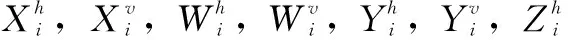
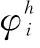
4 仿真算例

为了验证本文所设计的控制方案的有效性，本节将给出一个Darboux方程的仿真算例。

Darboux方程可以描述气体吸收、水蒸汽加热和空气干燥的一些线性过程。该方程描述如下[25]：

c0，σ(x，t)s(x，t)+dσ(x，t)f(x，t)

其中：s(x，t)是空间x∈[0，xf]和时间t∈[0，∞)处的未知函数，u(x，t)是给定的输入函数，σ(t，k)表示的是{1，2}中取值的在切换信号，c0，i，c1，i，c2，i和di是实系数，其中i=1，2。

定义：

令

xh(t，k)=s(k，t)=s(kΔx，t)，

xv(t，k)=r(k，t)=r(kΔx，t)，

u(t，k)=f(k，t)=f(kΔx，t)，

σ(t，k)=σ(kΔx，t)

需要注意的是，在文献[25]中，是对Darboux方程经过处理之后，将两个状态变量r和s均离散化处理之后得到的一个2-D离散系统方程，本文借鉴了文献[25]的处理方法并加以变化，继而通过上述的处理可以将Darboux方程其中的关于x方向上的变量离散化处理，另外一个关于t方向上的变量依旧保留为连续的变量，这样处理就可以得到一个由Darboux方程转变而来的切换2-D连续离散系统的方程。将Darboux方程中的元素定义成所需要的形式，并考虑上述系统在实际中会出现执行器饱和的情况，则可将其写成系统(6)的形式，其中：

qσ(t，k)=(c1，σ(t，k)c2，σ(t，k)+c0，σ(t，k))Δx，

得到系统所需要的参数矩阵之后，通过对于其中的变量进行赋值，就可以得到仿真所需要的数值矩阵。

需要注意的是，文献[25]也研究了Darboux方程，但该文献没有考虑实际中存在切换以及执行器饱和的情况。而在本文中，不仅考虑了执行器饱和的情况，还考虑了切换现象的存在，因此文献[25]所提出的控制器设计方案无法直接用于本文所研究的系统。为此，将利用本文所提出的控制器设计方法进行控制器设计。

Darboux方程系统参数设为：

c0，1=0.5，c0，2=0.5，c1，1=0.3，

c1，2=0.2，c2，1=-0.6，c2，2=-0.61，

d1=d2=0.05，Δx=0.5(N=2)

从而可以得出系统矩阵如下：

本次仿真实验的控制目标是设计事件触发条件(7)和(8)，控制器u(t，k)与切换信号σ(t，k)，使得闭环系统的状态是指数收敛的。

选取如下的设计参数：

a1，1=a1，2=0.25，a2，1=a2，2=0.47，

b1，1=b1，2=0.16，b2，1=b2，2=0.14，

∂=0.51

求解定理2中的线性矩阵不等式，可以得到可行解如下所示：

进而可以得到：

系统初始状态取为xh(0，k)=0.6，k=1，2，xh(0，k)=0，k≥3，xv(t，0)=0.24，t≤0.1，xv(t，0)=0，t>0.1，图2与图3分别给出了闭环系统水平状态和垂直状态的轨迹图。从图中可以看出，所考虑系统的水平状态和垂直状态均可以收敛到零。图4和图5给出了系统控制输入和切换信号的演化曲线。图6给出了系统的事件触发序列和事件触发次数。从图中可以看出闭环系统只发生了748次触发，说明信号只传输了748次，并且切换信号都是发生在触发时刻上，可以避免切换次数的频繁发生。控制输入的幅值也都没有超过最大值1。仿真结果可以表明，本文所提出的事件触发控制方案在执行器存在饱和情况下，不仅能够很好的保证闭环系统的稳定性，还能有效地利用系统的通信资源，从而避免不必要的浪费。从而表明本文所提出的控制设计方案的可行性与有效性。

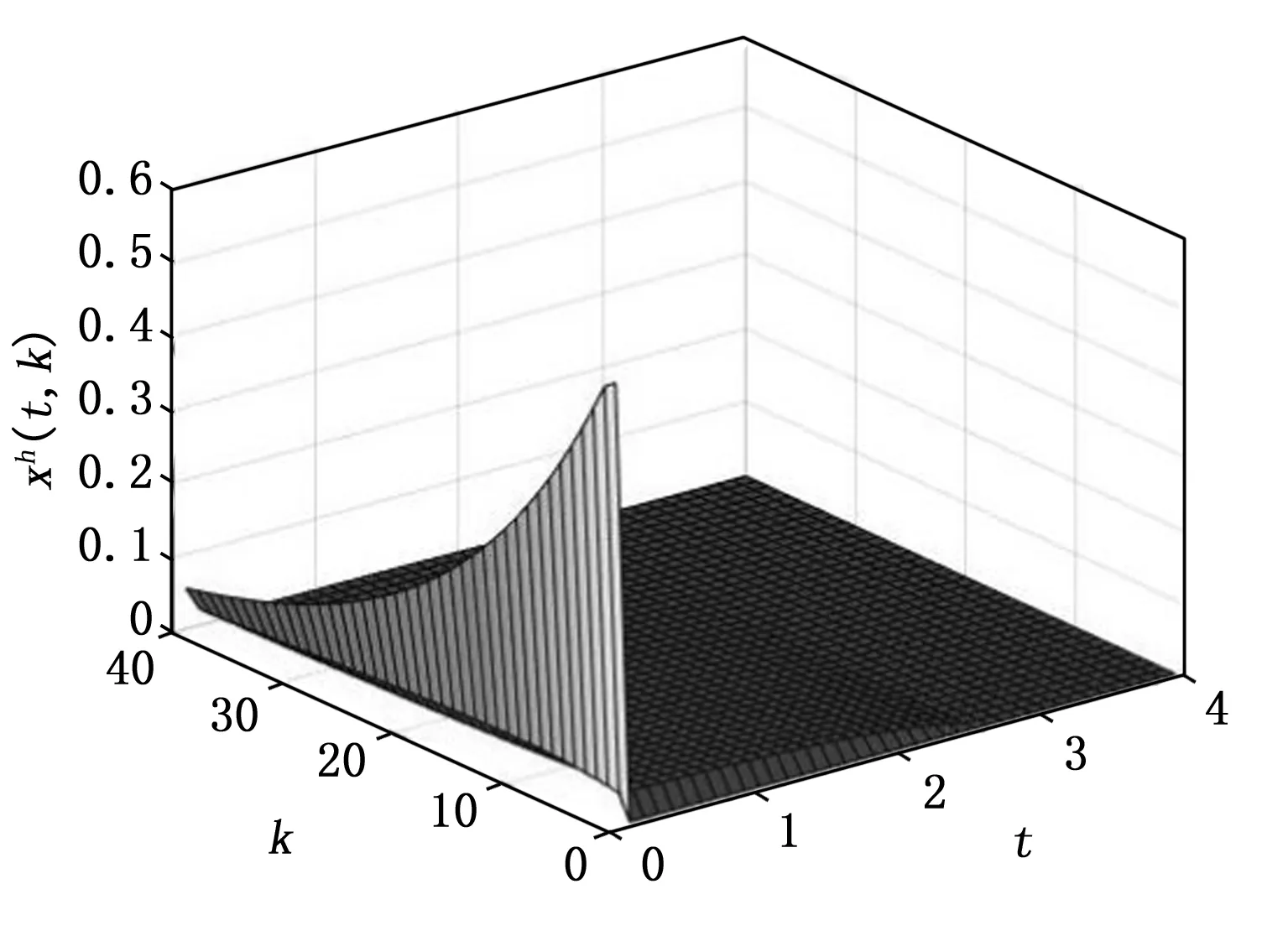
图2 ∂=0.51时状态xh(t，k)的轨迹

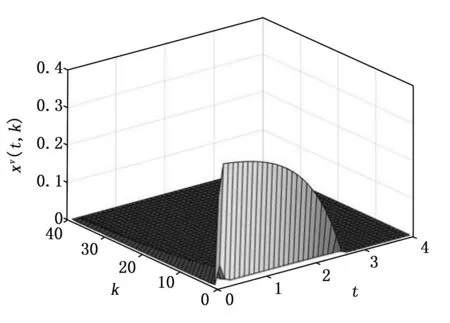
图3 ∂=0.51时状态xv(t，k)的轨迹

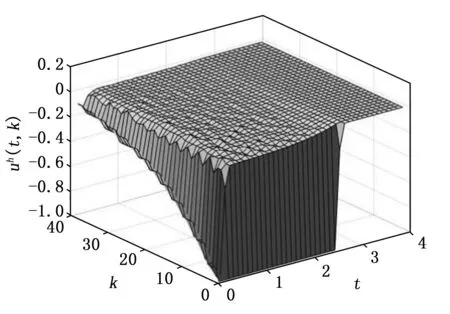
图4 控制输入uh(t，k)的演化曲线

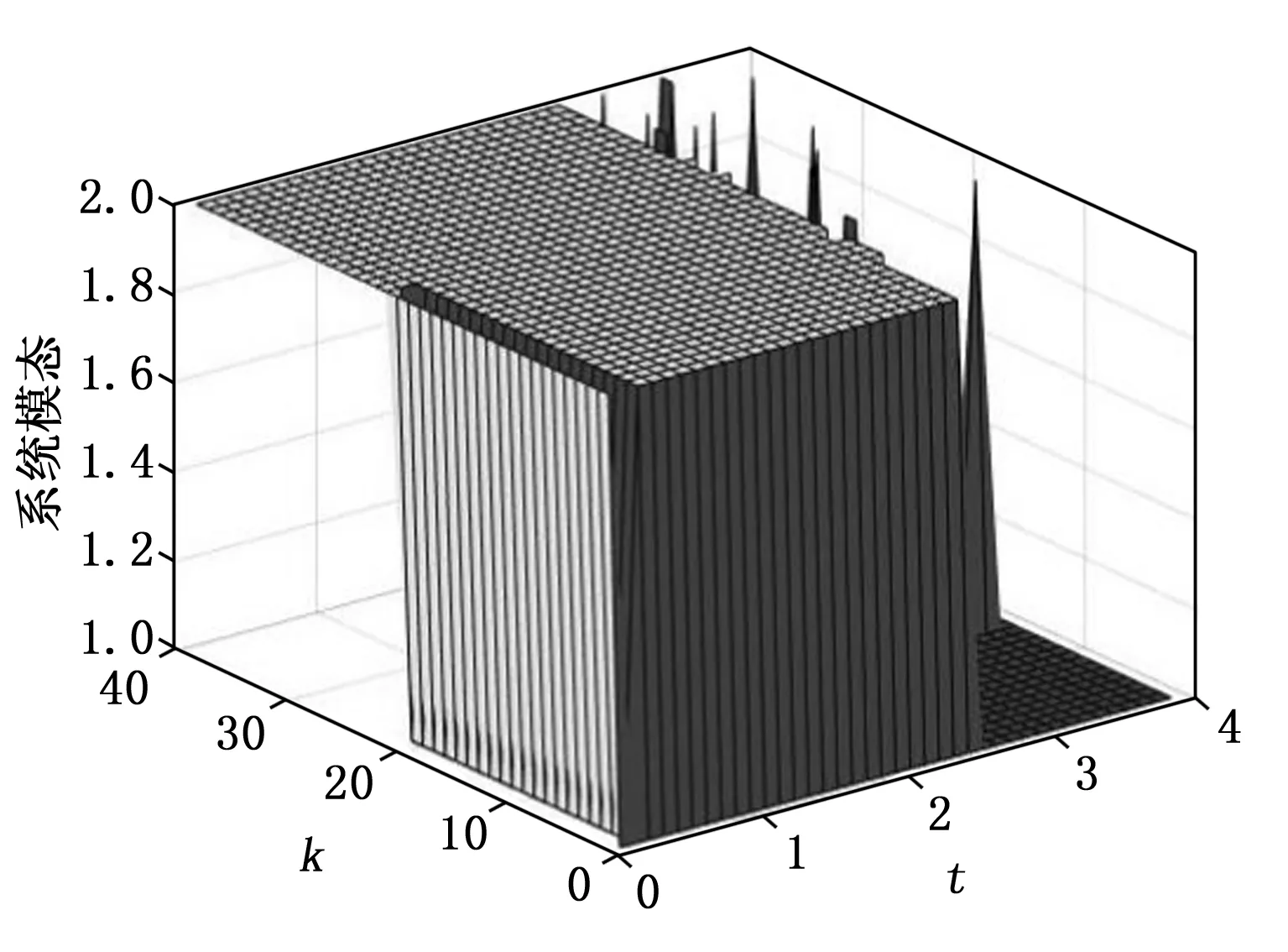
图5 切换信号

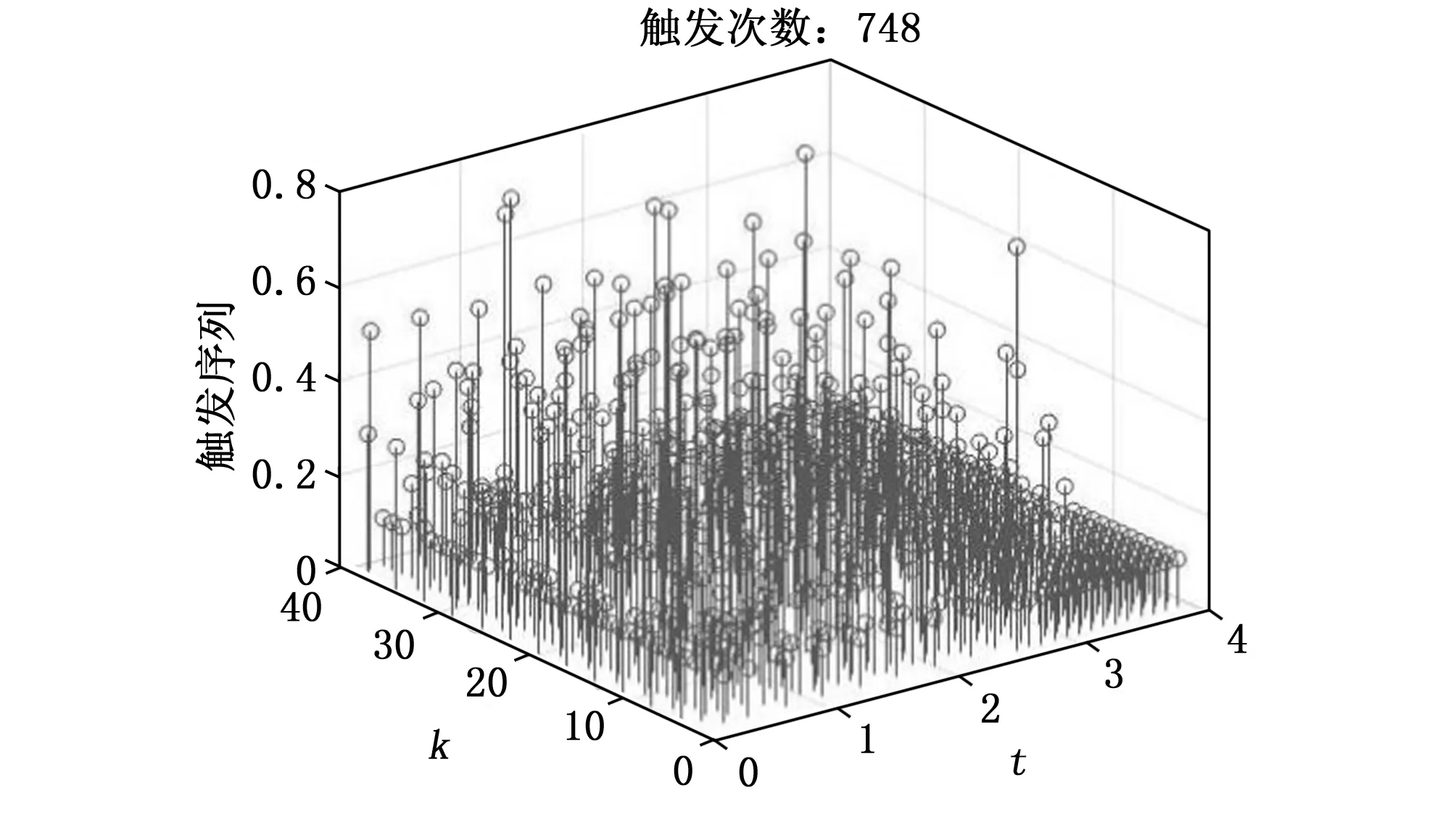
图6 ∂=0.51时的事件触发序列和事件触发次数

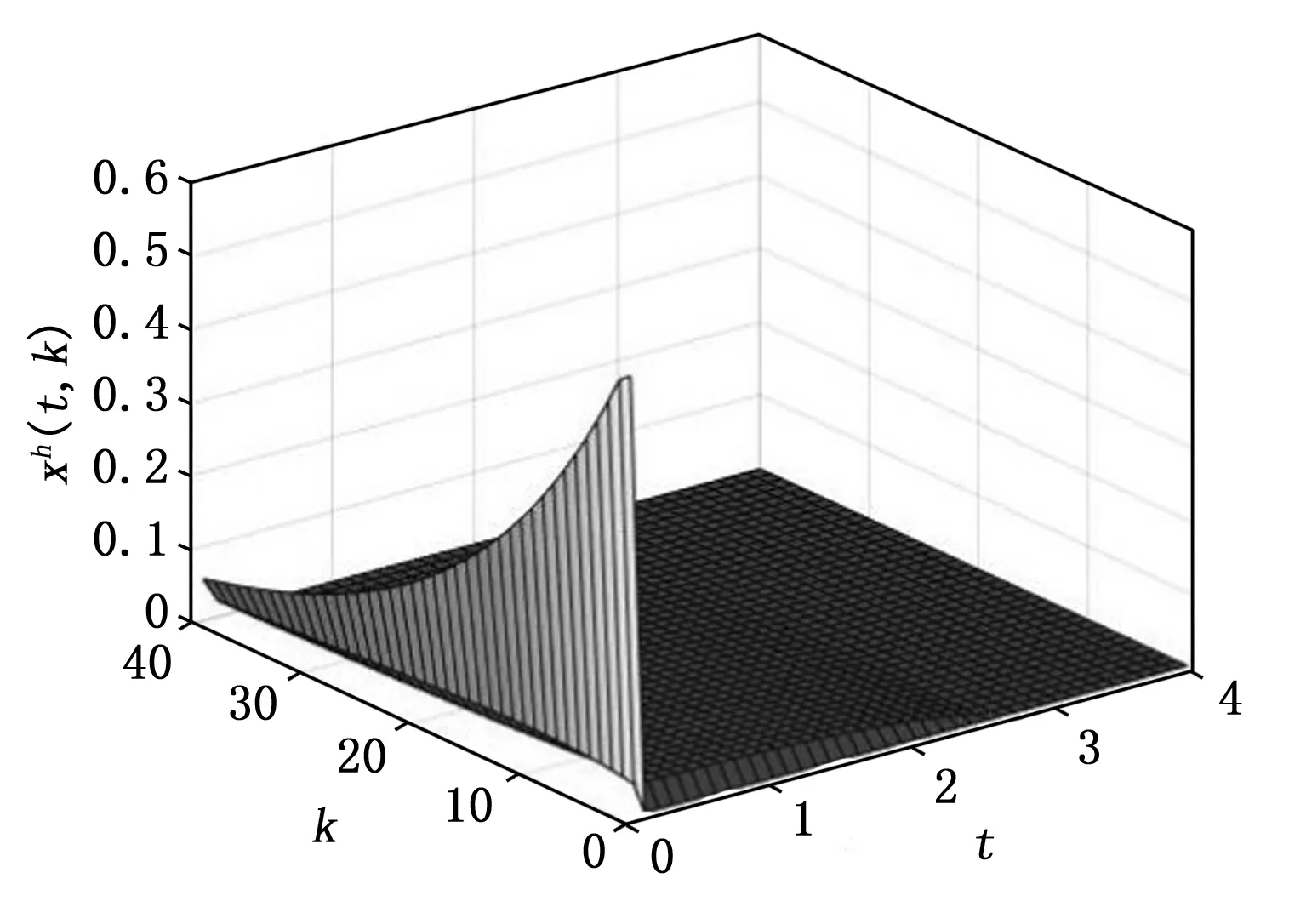
图7 ∂=1时状态xh(t，k)的轨迹

此外，我们还研究了参数∂的不同取值对于该算例的可行解的影响。通过仿真求解，我们得知只有当∂≥0.51时系统才有可行解，可见∂的取值对于该系统的可行解有比较大的影响。表1给出了∂取不同值时与触发次数之间的关系。图7和图8给出了∂=1时闭环系统水平状态和垂直状态的轨迹图，可以看出和∂=0.51时系统的状态轨迹图差别不大。图9给出了∂=1时系统的事件触发序列和事件触发次数。从表1、图6与图9可以看出，∂=0.51时的触发次数是最少的，当∂越来越大，触发次数逐渐变多。特别的，当∂=1时，也就是本文所提出的事件触发条件(7)和(8)就退化成文献[24]中所给出的事件触发条件时，触发次数是最多，可见本文所提出的事件触发控制的效果是优于文献[24]中所提出的事件触发控制的，在保证相近的系统性能时，可以进一步减少事件触发的次数，从而进一步减少通信通道的冗余和降低执行器的损耗，由此说明了本文所提方法的优越性。

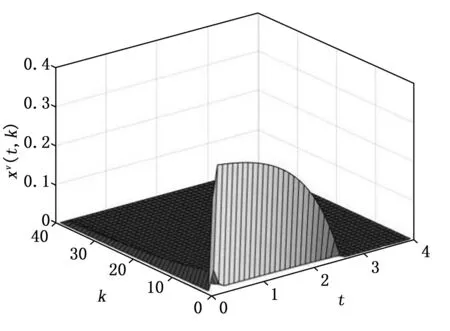
图8 ∂=1时状态xv(t，k)的轨迹

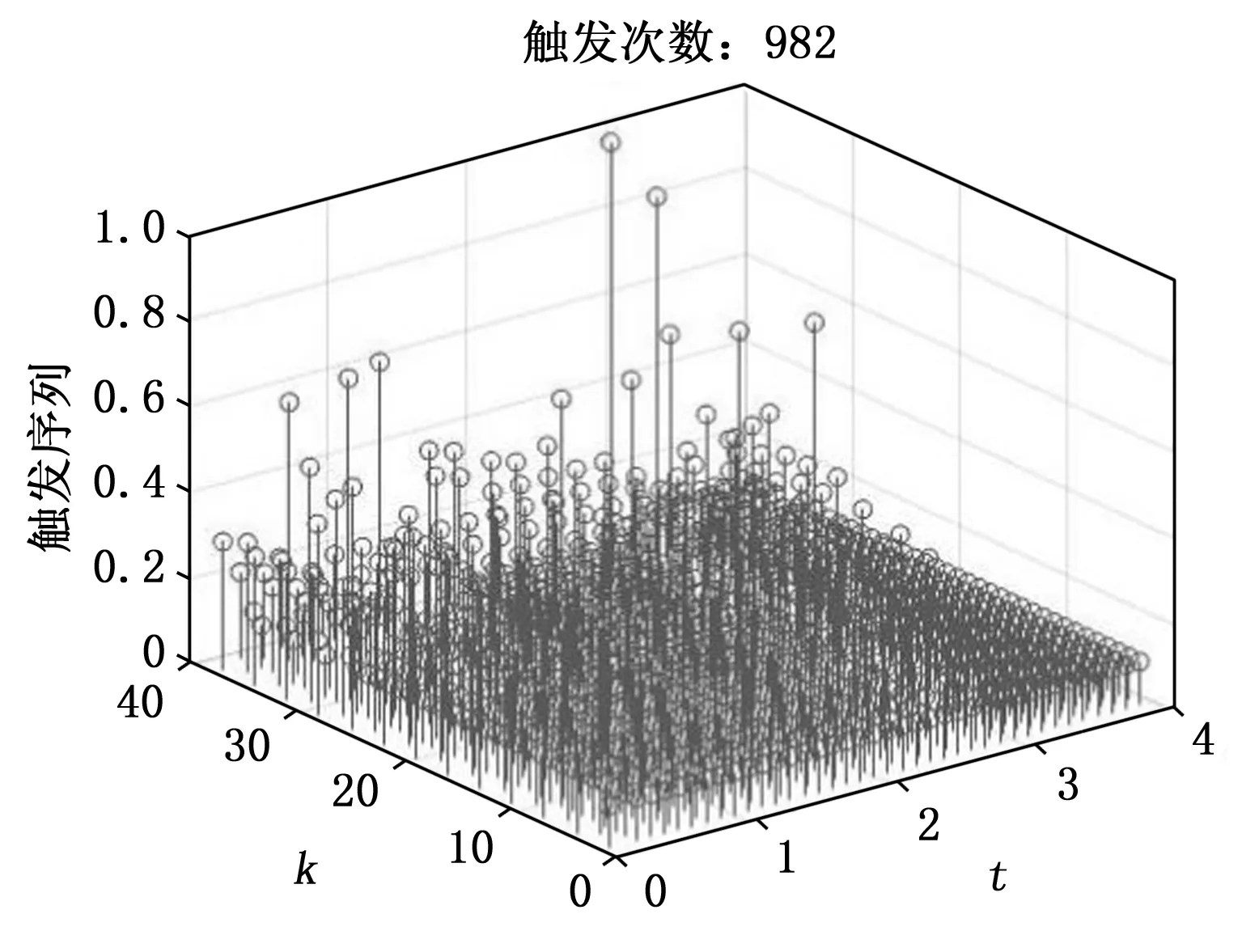
图9 ∂=1时的事件触发序列和事件触发次数

表1 ∂的取值与触发次数之间的关系

5 结束语

本文针对具有执行器饱和的切换2-D连续离散系统，提出了一种事件触发控制方案。利用凸组合技术将饱和非线性表示成一组凸包的线性组合，采用多Lyapunov函数法设计了一种考虑到系统饱和特性的事件触发机制和与之相关的状态依赖切换信号以及状态反馈控制器，并以线性矩阵不等式的形式给出了控制器增益矩阵和事件触发参数矩阵存在的充分条件。本文所提出的控制方案在保证闭环系统指数稳定的同时，可进一步减少通信资源浪费和执行器的损耗。最后通过一个仿真算例验证了本文所提出的控制方案的有效性与优越性。在未来的工作中，将重点研究具有执行器饱和的切换2-D连续离散系统的事件触发动态输出反馈控制问题，以及该系统存在传输时延或网络攻击的事件触发控制设计问题。