胡中惠，沈 丹，王 磊，杨申申

(1. 中国船舶科学研究中心, 江苏 无锡 214082；2. 深海技术科学太湖实验室, 江苏 无锡 214082；3. 深海载人装备国家重点实验室, 江苏 无锡 214082)

0 引 言

水下无人航行器（autonomous underwater vehicle，AUV）具有自主决策和控制能力，在海洋安全、海洋开发、海洋科研等领域发挥重要作用，是世界海洋强国竞相发展的重要装备之一[1]。航行控制，特别是航行过程中对航向和深度的控制是AUV 高效执行水下任务的重要基础。国内多位学者在AUV 航向和深度控制方面做了一系列研究工作，罗建超[2]、雷江航[3]、饶志荣[4]、李泽宇[5]、梅新华[6]等采用垂直面运动数学模型对AUV 的深度控制进行研究，胡坤[7]、聂为彪[8]、于浩洋[9]、陈恳[10]等采用水平面运动数学模型对AUV 的航向控制进行了研究。

水平面/垂直面运动数学模型是在平面运动假设的前提下简化分解而得到的，详细推导见文献[11]。平面/运动数学模型认为只改变航向而不改变深度，或只改变深度而不改变航向，并忽略2 个平面之间的耦合作用。但AUV 由于外伸信标、天线、推力器、舵翼、起吊点等多种附体，整体外形复杂，导致其空间运动具有非线性、强耦合的特点，AUV 在前进、变向的同时，还将伴随变深、姿态的变化，此时。单平面的运动数学模型将不再适用。因此，采用六自由度空间运动数学模型研究航行控制更能反映AUV 水下空间运动的真实情况，具有重要意义。本文以某AUV 为研究对象，基于六自由度空间运动数学模型，对AUV 进行受理分析。应用工程应用中常用的增量式PID 控制方法，通过仿真计算对比分析不同运动数学模型计算AUV 航向和深度控制时的运动规律，为AUV 的水动力及操纵面设计提供参考。

1 空间运动数学模型

1.1 坐标系

研究AUV 的水下空间运动时，采用通用的2 个右手坐标系，如图1 所示。一个是固定坐标系E-ξηζ，固定于地球；另一个是随体坐标系G-xyz，固定于AUV。

图1 坐标系Fig. 1 Coordinate system

1.2 数学模型

1.2.1 空间运动模型

在建立六自由度空间运动数学模型时，认为AUV 是一个刚体，AUV 在水下的空间运动可以看作一个刚体在流体中的空间机动。通过惯性坐标系与AUV 随体坐标系的转换，即可得到AUV 的空间运动模型[12]。

其中：X，Y，Z，K，M，N为AUV 所受的外力和外力矩，包括重力、浮力、推力器推力、水动力及力矩等，具体的受力情况和所研究的对象相关，需要具体分析。

1.2.2 受力分析

本文以某AUV（见图2）为研究对象。

图2 某AUV 外观图Fig. 2 Appearance of an AUV

AUV 的主要参数如表1 所示。

表1 某AUV 主要参数Tab. 1 Main parameters of an AUV

该AUV 通过尾部设置的推力器和十字舵实现水下空间运动的操纵与控制，通过对其受力分析，可得其所受外力和外力矩的数学模型如下：

AUV 在固定坐标系中的位置参数可表示为：

2 自动控制模型

自动控制采用工程应用中常用的增量式PID 控制方法实现AUV 的自动定向和自动定深。增量式PID 通过对系统偏差进行比例、几分、微分操作并线性组合成控制量，以减小系统误差，提高系统响应速度和响应效果。增量式PID 控制模型如下：

其中：

航向控制结构如图3 所示。

图3 自动航向保持结构Fig. 3 Automatic heading angle-holding structure

航向控制结构如图4 所示。

图4 自动深度保持结构Fig. 4 Automatic depth-holding structure

3 空间运动仿真计算

针对某型AUV，分别通过式（1）～式（8）建立空间运动数学模型以及平面运动数学模型，对AUV 典型的空间运动进行仿真计算和对比分析。

3.1 Z 形操舵运动仿真计算

Z 形操舵运动采用10°/10°操舵方法，采用空间运动数学模型和水平面运动数学模型分别进行仿真计算。其中，采用空间运动数学模型进行仿真计算时，对深度采用增量式PID 控制方法进行控制。仿真计算过程中，AUV 的航行速度为1.5 m/s，初始深度30 m，采样间隔为0.5 s，结果如图5 所示。

图5 10°/10°Z 形操舵特征曲线图Fig. 5 Characteristic curves of Z-shaped steering motion

可知，当采用空间运动数学模型进行仿真计算时，前2 个周期中，AUV 的操舵规律和首向角变化规律与水平面运动数学模型的计算结果基本一致。从第3 个周期开始，AUV 的操舵规律和首向角变化规律发生变化，如图6～图8 所示。

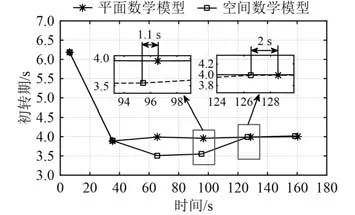
图6 初转期对比图Fig. 6 Comparison of initial turnaround periods

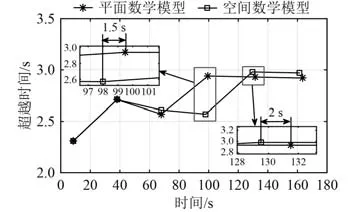
图7 超越时间对比图Fig. 7 Comparison of beyond times

图8 周期时间对比图Fig. 8 Comparison of cycle times

由图6 可知，在前2 个周期中，2 种数学模型计算得到的初转期一致。从第3 个周期开始，空间运动数学模型比平面运动数学模型计算得到的初转期小，其中第3 个周期小0.48 s。同时，空间运动数学模型计算的艏向角比平面运动数学模型提前1.1 s 达到10°；第4 个周期中初转期小0.42 s，提前2 s 达到10°。到第5 个周期时，2 种数学模型计算得到的初转期恢复一致，保持在4 s 左右，但空间运动数学模型计算的首向角始终比平面运动数学模型提前1.1 s 达到10°。

由图7 可知，在前3 个周期中，2 种数学模型计算得到的超越时间一致。第4 个周期中，空间运动数学模型比平面运动数学模型计算得到的超越时间小0.36 s。同时，空间运动数学模型计算的超越角比平面运动数学模型提前1.5 s 达到峰值。到第5 个周期时，2 种数学模型计算得到的超越时间恢复一致，保持在3 s左右，但空间运动数学模型计算的首向角始终比平面运动数学模型提前2 s 达到峰值。

由图8 可知，在前2 个周期中，2 种数学模型计算得到的周期时间一致。从第3 个周期开始，空间运动数学模型比平面运动数学模型计算得到的周期时间小，其中第3 个周期小1.16 s。同时，空间运动数学模型计算的艏向角比平面运动数学模型提前0.72 s 进入下一个周期；第4 个周期中周期时间小1.33 s，提前2 s 进入下一个周期。到第5 个周期时，2 种数学模型计算得到的周期时间恢复一致，保持在32 s 左右，但空间运动数学模型始终比平面运动数学模型提前2 s 进入下一个周期。

上述操舵规律和首向角变化规律的不同将导致运动轨迹的不同，运动轨迹对比如图9 所示。

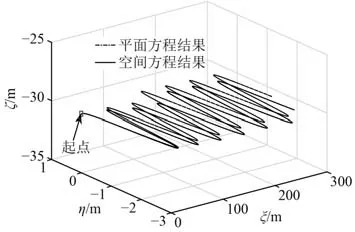
图9 运动轨迹对比图Fig. 9 Comparison of movement trajectories

可知，采用2 种数学模型仿真得到的AUV 运动轨迹并不重合，存在一定的差别。因为AUV 整体外形的不对称，导致AUV 在水平面内运动时伴随着垂直面内的运动，为保证AUV 水平面运动的稳定性，需要对垂直面内的运动进行控制。在使用空间运动数学模型进行仿真计算时，对深度采用增量式PID 控制方法进行控制，PID 参数值为KP=0.7，KI=1.1×10-4，KD=0.01。深度控制结果如图10 所示，水平舵操舵如图11 所示。

图10 深度变化图Fig. 10 Depth with time

图11 水平舵舵角变化图Fig. 11 Horizontal rudder angle with time

由图10 可知，如果AUV 在进行Z 形操舵运动时不对深度进行控制，则AUV 将由于整体外形不对称产生的力及力矩而同时向更深的方向运动，该运动将反向影响AUV 水平面内的运动。因此，AUV 在进行水平面内的运动时，同时需要对垂直面内的运动进行控制，转动水平舵抵消整体外形不对称产生的力及力矩引起的深度变化。由图11 可知，水平舵舵角最终稳定在0.26°左右，AUV 深度保持在30.15 m 左右，AUV 实现水平面内运动的稳定。

3.2 航向与深度保持仿真计算

AUV 在实际航行过程中，航向与深度往往需要同时保持，这也是AUV 空间机动能力的体现。本文分别采用空间运动数学模型和平面运动数学模型进行航向与深度保持仿真计算，计算类型划分如表2 所示。

表2 计算类型Tab. 2 Type of calculation

仿真计算过程中，AUV 的航行速度为1.5 m/s，初始航向0°，初始深度0 m，采样间隔为0.5 s，3 种模型采用相同的控制律。其中，航向控制的PID 参数为KP=0.15，KI=1.0×10-4，KD=0.01，深度控制的PID 参数为KP=0.7，KI=1.1×10-4，KD=0.01。计算结果如图12～图15 所示。

图12 航向角控制对比图Fig. 12 Comparison of heading angle control

图13 垂直舵舵角变化对比图Fig. 13 Comparison of vertical rudder angle

图14 深度控制对比图Fig. 14 Comparison of depth control

图15 水平舵舵角变化对比图Fig. 15 Comparison of horizontal rudder angle

通过图12 和图13 可以看出，对于航向的机动与保持，在相同控制律的情况下，采用空间运动数学模型比水平面运动数学模型的上升时间长9 s，采用空间运动数学模型计算的航向角最终稳定在61.6°，采用水平面运动数学模型计算的航向角最终稳定在61.3°，基本一致。也就是说，当AUV 在水下进行空间机动时，深度机动会导致航向机动响应变缓，但对最终的控制效果无影响。

通过图13 和图14 可以看出，对于深度的机动与保持，在相同控制律的情况下，采用空间运动数学模型比垂直面运动数学模型的上升时间长9 s，超越深度小0.35 m，采用空间运动数学模型计算的深度最终稳定在29.9 m，采用垂直面运动数学模型计算的深度最终稳定在29.8 m，基本一致。也就是说，当AUV 在进行水下空间机动时，航向机动会导致深度机动响应变缓，超越深度变小，但对最终的控制效果无影响。

4 结 语

本文以某AUV 为研究对象，基于六自由度空间运动数学模型，对AUV 进行受力分析，应用工程中常用的增量式PID 控制方法，形成AUV 水下空间运动自动控制仿真计算的数学模型。分别采用空间运动数学模型和平面运动数学模型进行典型空间运动仿真计算。通过对比分析可以看出，当AUV 在水下进行空间运动时，其水平面运动与垂直面运动之间的耦合作用不可忽略，该耦合作用将直接影响AUV 的操纵律和空间运动的控制律。本文研究结果可为AUV 水下空间运动的自动控制研究提供参考，具有一定的工程价值。