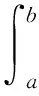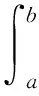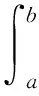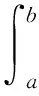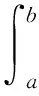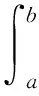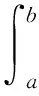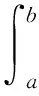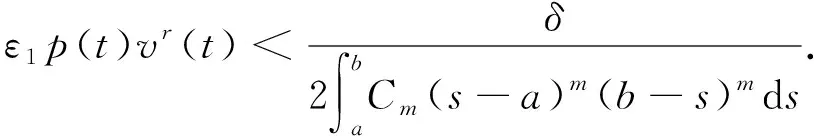李 阳

(西安电子科技大学 数学与统计学院,西安 710126)

1 引言与预备知识

考虑环域上2m阶半正椭圆方程:

(1)

若f(|x|,0)≥0,则问题(1)称为正问题.这类问题已被广泛研究[1-3].如文献[1]研究了环域上2m阶半线性椭圆方程

(2)

在g1∈C([a1,b1],[0,∞)),f1∈C([0,∞),[0,∞))且f1是超线性的条件下证明了该问题至少有一个正径向解,其中m≥1是一个正整数,D={x∈N;a1<|x|

当f(|x|,0)<0时,问题(1)称为半正问题[4].目前,对于二阶微分方程半正问题的研究已有很多结果[4-10].如Kajikiya等[7]研究了环域上半正椭圆方程

正径向解的存在性,其中θ>0是一个参数,A1={x∈N;a2<|x|

对于双调和及多调和微分方程半正问题径向解的研究目前报道较少,因此,本文将在半正即f(|x|,0)<0的情形下,用拓扑度理论研究带参数λ的2m阶半正椭圆方程(1)正径向解的存在性.

注1与正问题的处理方法不同,本文直接对半正问题(1)获得正解进行研究有一定的困难,从而考虑构造一个大于等于0的函数f*,并借助非共轭算子(-1)mΔmu的主特征值对应的特征函数φ构造一个新的边值问题进行研究,进而找到原问题(1)至少存在一个正径向解.

注2m=1的情形与m≥2的情形有本质区别:

1) 当m=1时上下解方法成立,但当m=2时,上下解方法成立一般需一定的单调性条件[11];

2) 二阶Dirichlet边值问题

极大值原理成立的区间是λ1∈I1=(-∞,π2),其中f2∈C([0,∞],[0,∞)).四阶非齐次两端简单支撑边值问题

极大值原理成立的区间是λ2∈I2=(-π4,950.884 3),其中f3∈C([0,∞],[0,∞))[11].观察到I1是一个无限区间,I2是一个有限区间,因此二阶问题和四阶问题有本质区别.

下面通过变换将求径向解的问题(1)转化为相应的带拟导数的常微分边值问题,并给出该问题对应齐次Dirichlet边值问题格林函数的一些性质.

设L表示Laplace算子的极坐标形式,即

则问题(1)可化为一维边值问题

(3)

因此,

L0v(t)=v(t);Lkv(t)=L(Lk-1v(t)),k=1,2,…,m.

特别地,有

定义算子l:C2m([a,b])→C([a,b]),lu(t)=(-1)mLmu(t).

引理1[2]齐次Dirichlet边值问题

有且仅有一个格林函数Gm(t,s),其中Gm(t,s)有以下性质:

1)Gm(t,s)>0,a

2) 存在Cm>0,使得0≤Gm(t,s)≤Cm(s-a)m(b-s)m,a≤t,s≤b;

本文的工作空间是

其范数为

2 主要结果

本文假设:

(H1)f∈C([a,b]×[0,∞),);

(H3)f(|x|,0)<0.

证明: 考虑Dirichlet边值问题

(4)

其中c≥0,φ表示l的主特征值α1对应的特征函数.

断言: 问题(4)有正解当且仅当c有界.

事实上,定义算子A:C([a,b])→C([a,b]),

显然A:C([a,b])→C([a,b])是全连续的.

由于

(5)

设问题(4)的正解为u(t),则

(-1)mLmu=f*(t,u)+cφ.

(6)

将式(6)两端同时乘以φ,并在[a,b]上进行积分,可得

通过简单的计算并结合式(5),可得

即

因为φ>0,所以

当c有界时,由问题(4)的等价积分形式可得

对任意的t∈[a,b],有

当c=0时,问题(4)为

(7)

结合f*(t,u(t))在[a,b]上的有界性及问题(7)的等价积分形式,对任意的t∈[a+δ,b-δ],存在充分小的r1∈(0,r2),使得

从而

‖u‖C2m-1≥‖u‖C0>r1.

下证对任意的0≤ν≤1,当u∈∂Br1时,有u≠νF(u).

其解为

当t∈[a+δ,b-δ]时,结合r1充分小,可保证

从而‖u‖C2m-1≥‖u‖C0>r1,与u∈∂Br1矛盾,因此结论成立.

由拓扑度理论的缺方向性和不动点指数理论,可得

deg(I-F,Br2,0)=0, deg(I-F,Br1,0)=1,

从而

证毕.

‖F1(v)‖C2m-1<δ,

(8)

则存在0

u=F(u)+F1(u).

(9)

证明: 沿用引理2的记号,设

下面分三步证明:

1) 由F的紧性,证明存在δ>0,使得若v∈∂Nε,则有‖(I-F)(v)‖C2m-1>δ.

若u满足lu(t)=f(t,u)=p(t)ur,不妨设其解为u1,u2,由于v∈∂Nε,则v不是u1,u2其中之一,进而v不是lu(t)=f(t,u)的解,因此(I-F)(v)≠0,从而‖(I-F)(v)‖C2m-1>δ.

2) 证明对于充分小的ε>0,当v∈Nε时,对任意的t∈(a,b),有v(t)>0.

(10)

于是问题(10)的解为

3) 证明存在0

由于‖F1(v)‖C2m-1<δ,v∈Br2,则对任意的v∈∂Nε,有

‖(I-F-F1)(v)‖C2m-1≥‖(I-F)(v)‖C2m-1-‖F1(v)‖C2m-1>0,

因此(I-F-F1)(v)≠0,从而deg(I-F-F1,Nε,0)有意义.结合拓扑度理论的性质有

证毕.

引理4若f满足假设(H1)～(H3),则存在λ0>0,使得对任意的0<λ<λ0,问题(3)至少有一个正解.

证明: 由已知条件,存在ε1>0,使得对任意的t∈[a,b],当ξ充分大时,有

因此对这样的ξ,有

|f(t,ξ)-p(t)ξr|<ε1p(t)ξr,

从而存在常数k(ε1),使得对任意的ξ≥0,有

|f(t,ξ)-p(t)ξr|<ε1p(t)ξr+k(ε1).

(11)

令

由于

因此

对任意的0

取ε1充分小,使得对任意的t∈[a,b],有

(12)

取α充分小,使得

(13)

从而

(14)

结合式(12),(13),可知式(8)成立.

由引理3知,存在0

(15)

定理1若f满足假设(H1)～(H3),则存在λ0>0,使得当0<λ<λ0时,问题(1)至少有一个正径向解.

证明: 事实上,u是问题(1)的一个径向正解当且仅当u是问题(3)的一个正解.因此引理4成立即表明定理1成立.