黄虎 田泽冰

(上海大学力学与工程科学学院,上海市应用数学和力学研究所,上海市能源工程力学重点实验室,上海 200072)

波-波共振机制,无论在微观物质还是在宏观物质的能量传播、分布进程中都起着一种根本、突显的作用.对于地球上最为广阔、直观的海洋表面波运动,势必更加如此而可观可知.那么,可否从中提炼出一般的波-波共振规律? 尤其是最为特殊、简要的单波列共振法则.为此,依据Phillips 开创现代水波动力学而提出特定4-波共振条件的经典一整套方式方法,从基本的海洋深水表面张力波-重力波控制方程组出发,运用Fourier-Stieltjes 变换和摄动方法依次给出自由表面位移的Fourier 分量的第一阶微分方程和愈来愈复杂却趋于完整的第二、三、四阶积分微分方程,在一套自创、自明而又简洁的符号体系下依次求解这些方程而求得其单波列第一阶自由表面位移和第二、三、四阶非共振与共振自由表面位移的Fourier 系数以及第二、三、四阶共振条件,从而顺势推断出一般的单波列第 n 阶自共振定律.这就完整揭示了海洋表面张力波-重力波之单波列共振动力学的丰富内涵,有效扩展了海洋表面重力波之经典Phillips 共振单波列解的适用范围,为刻画海洋表面波之双波列、更多波列的单重、多重共振相互作用机制奠定了基石,因而在全部波动领域的单波列共振规律的探寻上提供了一种典型范例.

1 引言

波之运动,可贯穿所有物质时空.大致说来,纷繁多样的波可划分为两大类: 双曲波和色散波[1].后者,即以地球上最为广阔、直观的海洋表面波为其典型代表.现代水波动力学,始发于20 世纪60年代初表面重力波第三阶四波共振的Phillips 解[2].波-波共振在动理学方程的建立[3]、双波列的最简计算[4]、能量共享机制更为清晰的阐明[5]、非线性共振相互作用的简化[6]、实验证实[7,8]等等方面上引发了一系列经典结果.目前,适用于Bose-Einstein 凝聚[9]、非线性光学[10]、海洋表面波[11]和内波[12]、宇宙开端的重力波[13]等几乎所有物质波运动尺度、具有极大普适性的波湍流[14-17]的立足点,正是集中性地表现于海洋波-波共振的动理学方程[3,11,12,18-20]上.

海洋表面波,可以是纯粹的表面张力波或重力波,或表面张力波-重力波[17,21,22].最近,从实验上观察到在表面张力波-重力波交叠处的非局部三波列共振现象[23,24]: 既可在通常的表面张力波-重力波之间发生,也可在以往不允许的表面重力波之间发生.这就涉及雷达直接观测表面张力波、潜艇航行等相关的一系列海洋活动、工程相关问题,必将对表面重力波固有的频率适用范围产生影响.波-波共振,可以是一重的单波列或多波列[25,26]或多重的单波列或多波列[27].这两种情形就指向一种最基本的复合波态: 单波列之表面张力波-重力波的波-波共振.其若从低阶向高阶以至于第n阶演化下去,则其所对应的共振条件是什么? 未知.则多重多波共振条件更是无从回答.唯有前者获得精准结果,方可使后者有所凭依,最终求得确切答案,也才能弥补经典深水表面重力波的Stokes 波理论[28,29]和Phillips 共振解[2]在共振上遗留下的历史空白,也才使得与普适的Hamilton 函数[17,30,31]密切关联的现今动力学方程[17,32]及其系综平均的动理学方程[3,11,12,18-20]得以极大扩展和统一刻画.

目前,存在着深水表面张力波-重力波的第二阶三波共振条件[33]和深水重力波的第三阶四波[2]、第四阶五波[34]、第五阶六波[35]的共振条件.较之单一的重力波,表面张力波-重力波的单波列从低阶到高阶的自共振传播无疑具有更为丰富的内涵和结构.从中,正所谓“道生一,一生二,二生三,三生万物”[36],可对应着从四面八方滚滚涌来的万顷波涛.

基于此,本文按照经典水波共振的Fourier-Stieltjes 变换[2],运用在科学、工程中大行其道的摄动方法[2,37,38],力求严格推论出深水表面张力波-重力波之单波列自共振由低阶至高阶的一般通用共振定律.

2 运动方程组及其Fourier-Stieltjes变换

假定存在一个无黏、无旋、不可压缩的深水海洋表面波运动.建立直角坐标系O-xyz: 原点O、水平坐标x=(x,y) 位于静水面上,竖直坐标z向上为正.速度势函数为ϕ(x,z,t),自由表面位移为ζ(x,t) .其中,t为时间.于是,深水海洋表面波的运动方程组可表述为

其中,dB(k,t) 和 dA(k,t) 可称为Fourier-Stieltjes变换,B(k,t) 和A(k,t) 则称为Fourier 系数[2],积分区域为整个波数矢量k平面,k=|k|.

据此,运动学边界条件(2)和动力学边界条件(3)可以Fourier-Stieltjes 变换依次表征为

其中,T=T′/ρ,dA和 dB为简洁起见而忽略了自变量t,B ′和B ′′依次代表对时间的第一、第二阶导数,Dn(n=1,2) 和H n(n=1,2,3,4) 的详细表达式可见文献[2].此外,

3 单波列各阶动力学方程

为求解方程(8),可对Fourier-Stieltjes 变换 dB(k,t) 进行摄动级数展开:

相应地,可得:

将(13)式代入(8)式,可得第一阶的微分方程和第二、三、四阶的各自积分微分方程:

4 B 和C 的下标符号约定

为规范、简要、明确地表示单波在一对或多对正负波数矢量点上的哪一阶共振与否的Fourier 系数B及其表达式里出现的系数C,特做出以下上下标规定.

1) 第一阶各量只有一个下标,均为1.

2) 第二阶各量包含以一个减号相隔的两个下标: 第1 个下标均为2;第2 个下标以一个奇数m(表示“非共振”)或偶数“m+1 ”(表示“共振”)表征.某一对正负波数矢量点即以(m,m+1)刻画.第2 个下标也可围绕 (m,m+1) 而表征为“m,m+1”.

3) 第三阶各量包含以两个减号相隔的3 个下标: 第1 个下标均为3;第2 个下标均为1,即代表单波唯一一对第二阶正负波数矢量点处的非共振位移;第3 个下标同样以一个奇数m(表示“非共振”)或偶数“m+1 ”(表示“共振”)表征,同样也可表征为“m,m+1 ”.

4) 第四阶各量包含以三个减号相隔的4 个下标: 第1 个下标均为4;第2,3 个下标皆为1,依次表示在第二、三阶正负波数矢量点上的非共振位移;第4 个下标照样以一个奇数m(表示“非共振”)或偶数“m+1 ”(表示“共振”)表征,照样亦可表征为“m,m+1 ”.

5 单波列各阶共振条件

5.1 第一阶自由表面位移和色散关系

解方程(15),可求得:

其 中,K1=|K1|,δ(k) 表 示Diracδ函 数.(21)式即为单波列第一阶色散关系.实际上,这正是后续高阶共振条件的内在本质体现.

5.2 第二阶自由表面位移的Fourier 系数和共振条件

将(19)式代入(16)式,可得对积分有非零贡献的一对正负波数矢量点k: (±2K1)(1,2) .假设:

其中,K=(K′,K′′)=±2K1或K=(K′,K′′)=0,ε为一个任意小的正数.由(22)式可将(16)式化为

其中,

其中,

据此,可求得(24)式随时间线性增长的共振特解:

其中,

5.3 第三阶自由表面位移的Fourier 系数和共振条件

由(26)式可得:

将(19)式和(31)式代入(17)式,可给出有积分贡献的两对正负波数矢量点k: (±3K1)(1,2) ;(±K1)(3,4) .与前类似,在k的小区域内对(17)求k积分,可得:

由(32)式,可令K分别等同于上述两对波数矢量点k,则可得如下方程:

其中,

和(33)式随时间线性增长的共振特解:

其中,

显见,(34)式满足共振-色散关系(21)式,则可得其随时间线性增长的共振特解:

其中,

5.4 第四阶自由表面位移的Fourier 系数和共振条件

由前述可判知,若要发生第四阶共振,则须不发生第二、三阶共振.为此,由(37)式可得:

将(19)式、(31)式、(44)式代入(18)式,可给出有积分贡献的两对正负波数矢量点k:(±4K1)(1,2) ;(±2K1)(3,4) .再与前类似,在k的小区域内对(18)式求k积分,可得:

进而,在(45)式中可令K=k=±4K1,则得到:

其中,

和(46)式随时间线性增长的共振特解:

其中,

同样,可求出第四阶在另一对正负波数矢量点(±2K1)(3,4)上的非共振和共振的自由表面位移的Fourier 系数.于是,由上述第二、三、四阶自由表面位移的Fourier 系数可求出各阶非共振和共振的自由表面位移，进而求出第三、四阶在各自不同对正负波数矢量点处的若干典型组合位移，最终得出单波列从第一阶到第二阶直至第四阶的非共振和共振的若干自由表面总位移.

6 单波列第 n 阶自共振定律

单波列的第二、第三、第四阶自共振表达式已依次推出,它们均表现出鲜明的一致特征.据此,可顺势推断出单波列的第n阶自共振定律:

若海洋深水表面张力波-重力波的单波列自第二阶起始的第 (n-1) 阶波均不发生自共振,则第n阶波发生自共振的条件为

其中,κ表示表面张力与重力的比值,即著名的Bond 数的倒数.

依据深水海洋表面波的下列划分范围[27]: 表面张力波,n ＜0.5 ;表面张力波-重力波,0.5＜n ＜6.45 ;表面重力波,n ＞6.45,可给出单波列第n阶自共振定律(53)式的演变特征图1.从中可知,共振波数从“表面张力波”区域急剧地下滑到“表面张力波-重力波”过渡区域,然后平缓地进入“表面重力波”区域.在“表面张力波-重力波”区域内可发生5 种正整数阶共振:n=2,3,4,5,6 ;在“表面重力波”区域内可发生无穷多正整数阶共振:n=7,8,···.在“表面张力波”区域内则无共振,故以虚线表之.但是,纯表面张力波当可发生最低阶之第二阶的3-波共振[33].显见,上述划分的“表面张力波和表面重力波”并非纯粹,只是各以其主打“表面张力波-重力波”中的某种波.若从Navier-Stokes方程出发,则可发现存在一个无穷可数“波象(wave-like)”共振集合,可同胚于Cantor 有理数集合[39].(53)式所包容的大于1 的无穷多正整数阶共振集合便为其一个特定、典型的子集合,也可更为深刻、通透地以“波粒二象性(wave-particle duality)”加以刻画[40].

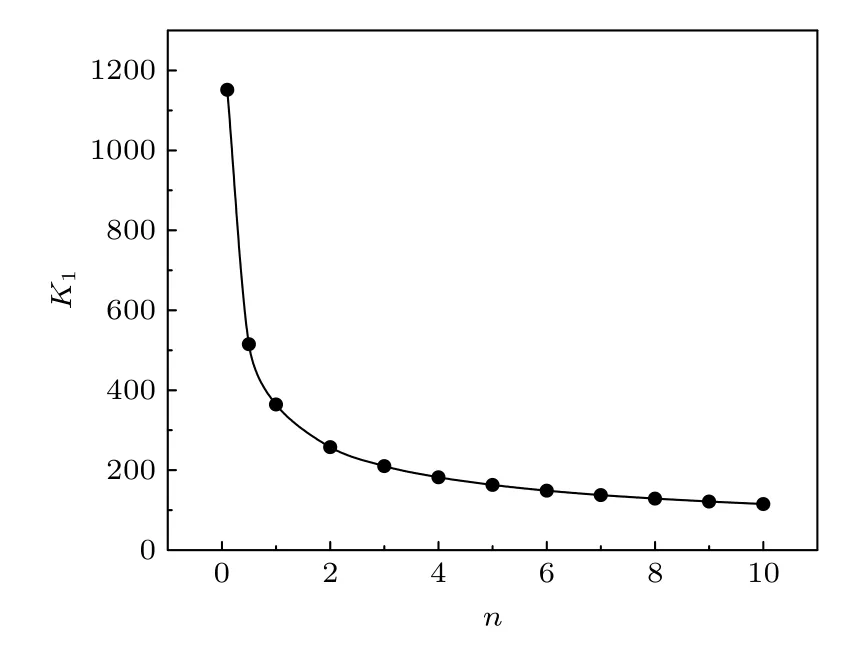
图1 深水海洋表面张力波-重力波的单波自共振定律,ρ =1000 kg/m3,g=9.81 m/s2,T ′=0.074 N/m,T=7.4×10-5 m3/s2Fig.1.Self-resonance law of one wave for ocean surface waves in deep water: ρ=1000 kg/m3,g=9.81 m/s2,T′=0.074 N/m,T=7.4×10-5 m3/s2 .

将自由表面位移的动力学边界条件方程作某种典型级数展开,将会发现在其各项的分母中出现幂乘积因子 (κn-1)[41].这就意味着存在一种可数无穷的内在共振族[27],也就给予共振定律(53)式一个充分证实.从(53)式中可以看出: 当n →∞时,K1→0 .这就预示着“物极必反”: 超大波长的波平浪静,或海流.所谓湖泊,所谓海洋,其动力学乃至于动理学的极致表现,大致在此.

在理论上,可继续对(53)式的第五、第六阶直至第n阶单波列持续进行一番循序渐进、愈来愈繁重的运算、求解、论证.从中,自可或可显出自共振定律(53)始终如一的特性.在实验上,可以精巧的构想、布局而证实(53)式.例如,可通过对重力环境的改变以达到表面张力和重力区域之间的理论变迁频率[22].的确,因推演、推断或猜想而一举成功的著名物理学定律、方程,总是数学物理或理论物理或应用数学向前推进的一座座不可或缺的里程碑.例如,石破天惊的牛顿运动定律、万有引力定律[42]和杨-米尔斯方程[43].

7 结论

水波,体现在色散性,重在与其他波动共存的共振性.以此,可将能量从低阶向高阶显著地传播、扩散下去,则最基本的单波列自共振一般特征不可不洞察.本文按照经典的Phillips 共振理论推导出单波列第二、三、四阶共振关系而从中推断出的海洋深水表面张力波-重力波的单波列自共振定律(53)式,即是一大典型实例.这就为深水海洋表面波的单重、多重[27]的双波列[25]、多波列[26]共振条件定律的提出奠定了基石,而基本的对称性[44,45]必蕴含在这些定律的构造中.从更为实际的波浪环境条件来看,共振定律(53)式受制于理想的深水波.若是较为实际的有限常水深波[46,47]呢? 更进一步的缓变[48]或陡变[49]的海底波呢? 再将环境流的作用纳入其中而包含基本、普遍的波-流-海底共振相互作用机制[50]呢? 无疑,(53)式可以充当这一切扩展的出发点、向导,进而积极推演,大胆预测,最终为与波-流-海底共振密切关联的能量海浪谱和具有极大普适性的波湍流之Kolmogorov-Zakharov-型谱[3,14-16,19-22]的深入、完整研制提供一个可靠的理论基础平台.