Zhenyu LIU, Yufeng LYU, Guodong SA, Jianrong TAN

Research Article

Reliability measure approach considering mixture uncertainties under insufficient input data

1State Key Laboratory of CAD&CG, Zhejiang University, Hangzhou 310058, China2Ningbo Research Institute, Zhejiang University, Ningbo 315100, China3Laboratory of Healthy & Intelligent Kitchen System Integration of Zhejiang Province, Ningbo 315336, China4School of Mechanical Engineering, Zhejiang University, Hangzhou 310058, China

Reliability analysis and reliability-based optimization design require accurate measurement of failure probability under input uncertainties. A unified probabilistic reliability measure approach is proposed to calculate the probability of failure and sensitivity indices considering a mixture of uncertainties under insufficient input data. The input uncertainty variables are classified into statistical variables, sparse variables, and interval variables. The conservativeness level of the failure probability is calculated through uncertainty propagation analysis of distribution parameters of sparse variables and auxiliary parameters of interval variables. The design sensitivity of the conservativeness level of the failure probability at design points is derived using a semi-analysis and sampling-based method. The proposed unified reliability measure method is extended to consider-box variables, multi-domain variables, and evidence theory variables. Numerical and engineering examples demonstrate the effectiveness of the proposed method, which can obtain an accurate confidence level of reliability index and sensitivity indices with lower function evaluation number.

Insufficient data; Reliability index; Sensitivity analysis; Sparse variable; Uncertainty propagation

1 Introduction

Uncertainties are ubiquitous in engineering pro ducts due to manufacturing error (Liu et al., 2022), lack of information, intrinsic random properties, etc. These uncertainties are quantified and propagated to uncertainties of product performance, which may lead to unexpected failure or performance fluctuation. Reliability analysis and reliability-based design optimization (RBDO) methodologies have been developed to obtain a reliable optimum design considering input uncertainties and have been applied in many engineering fields (Tostado-Véliz et al., 2021, 2022; Solazzi, 2022; Wakjira et al., 2022).

In traditional RBDO methodologies, the uncertainty variables are assumed to be determinate probabilistic variables (Sankararaman and Mahadevan, 2015). However, in many actual engineering applications, it is difficult to acquire the complete uncertainty information for calculating the accurate probability density functions of uncertainty variables under insufficient input data (Wang et al., 2016). According to the available amount of input sampling data, the uncertainty variables can be classified into statistical variables with sufficient input data (Type I), sparse variables with insufficient input data (Type II), and interval variables with little input data (Type III) (Oberkampf et al., 2004). With an increase of input sampling data, the interval variables can be converted to sparse variables or even to statistical variables; the sparse variables can be also converted to statistical variables when there are enough input sampling data.

The statistical variables (Type I) can be represented using determinate distribution type and accurate distribution parameters, such as normal distribution, gamma distribution,distribution, and Weibull distribution (Chen et al., 2003). A series of probabilistic uncertainty representation, propagation, and optimization design methodologies have been proposed to deal with statistical variables (Gan et al., 2018; El Haj and Soubra, 2021). The interval variables (Type III) can be represented using non-probabilistic methodologies, such as the convex model, evidence theory, fuzzy number, and-box (Ni et al., 2018). Many hybrid uncertainty analysis methodologies have also been proposed to deal with statistical variables and interval variables simultaneously (Hong et al., 2021).

The distribution parameters of sparse variables (Type II) cannot be fitted accurately due to the insufficiency of input sampling data, and the probabilistic uncertainty analysis methodologies for statistical variables cannot be used directly for the representation of sparse variables. If the sparse variable is represented using non-probabilistic methodologies for interval variables, much uncertainty information in the insufficient input data is missing. Therefore, how to represent the uncertainties of sparse variables accurately is one issue in reliability-based design optimization.

Initially, the sparse variables (Type II) are quantified using possibility-based approaches (Lee et al., 2013). For further parameterization of the sparse variables, likelihood-based approaches and Bayesian approaches are proposed to quantify their distribution types and distribution parameters. Uncertainty of distribution types can be estimated using many methodologies, such as the model identification method, Johnson distribution, and Kernel density estimation (Peng et al., 2017). Although the reliability index under sparse variables can be calculated, the algorithms are too computationally demanding due to the nesting estimation of uncertainty distribution types, distribution parameters, and uncertainty variables.

The second issue is how to accurately quantify the reliability index considering the three types of uncertainty variables simultaneously. The uncertainty propagation methodologies for statistical variables (Type I) have been widely studied, such as probability density evaluation (McFarland and DeCarlo, 2020), surrogation model (Yun et al., 2020), and importance sampling method (Liu and Elishakoff, 2020). Many uncertainty quantification methodologies of reliability index considering interval variables (Type III) have also been proposed, such as interval arithmetic techniques, global optimization approach, and perturbation methods, and are summarized by Faes and Moens (2020). The uncertainty propagation analysis for sparse variables (Type II) is a multiple-loop process, the distribution types and distribution parameters are estimated in the outer loops, and the reliability index is estimated in the inner loops using similar methods to those for statistical variables (Type I). To reduce computational complexity and increase the accuracy of the reliability index, many non-probabilistic reliability analysis methodologies for hybrid uncertainties have been proposed (Zhao et al., 2018; Wei et al., 2019). Although there are many reliability measure approa ches for mixture uncertainties, there are multiple loops for the uncertainty quantification and propagation analysis of sparse variables, and the non-probabilistic reliability index is difficult to integrate with many probabilistic RBDO algorithms. Therefore, a probabilistic reliability measure approach is proposed and the reliability index and sensitivity indices are calculated considering the three types of uncertainties simultaneously.

The rest of this paper is organized as follows. The reliability measure and sensitivity analysis problem considering mixture uncertainties is described in Section 2. In Section 3, a unified calculation algorithm of reliability index is proposed with less sampling loops and less sampling points. The sensitivity indices are calculated through a semi-analytical method based on auxiliary variables in Section 4. The proposed algorithm is extended for considering-box variables, multi-domain distribution variables, and evidence theory variables in Section 5. Three numerical and two engineering examples are demonstrated to verify the effectiveness of proposed methodology in Section 6. Conclusions are summarized in Section 7.

2 Failure probability under insufficient input data

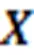
Fig. 1 Multiple uncertainty types due to insufficient input data. BPA represents basic probability assignment

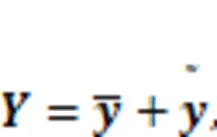
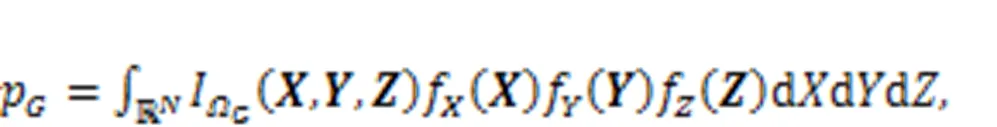
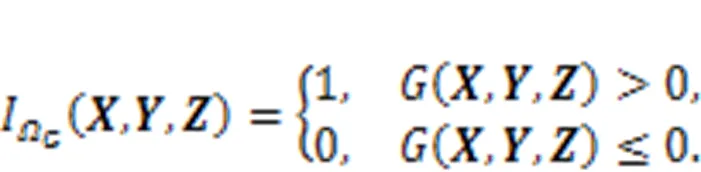
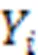
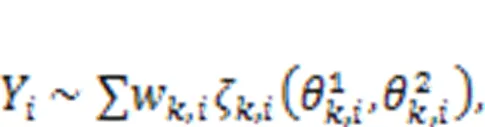
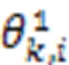
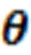
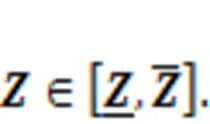
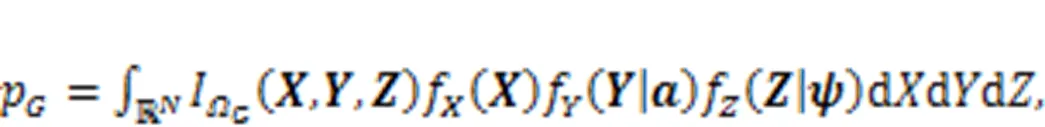
3 Unified calculation of probability of failure probability

3.1 Reliability measure based on auxiliary variable method

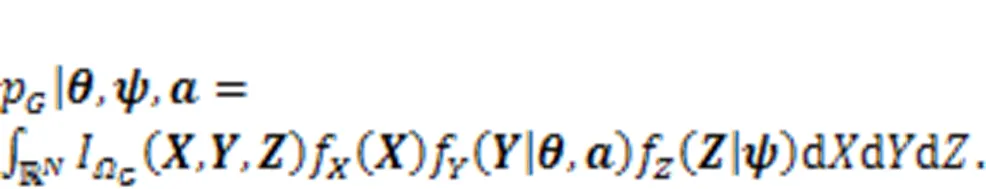
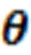
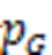
3.2 Calculation procedure of probability of failure probability

The step-to-step procedure is listed as follows, and the calculation flowchart is shown in Fig. 2.

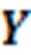
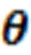
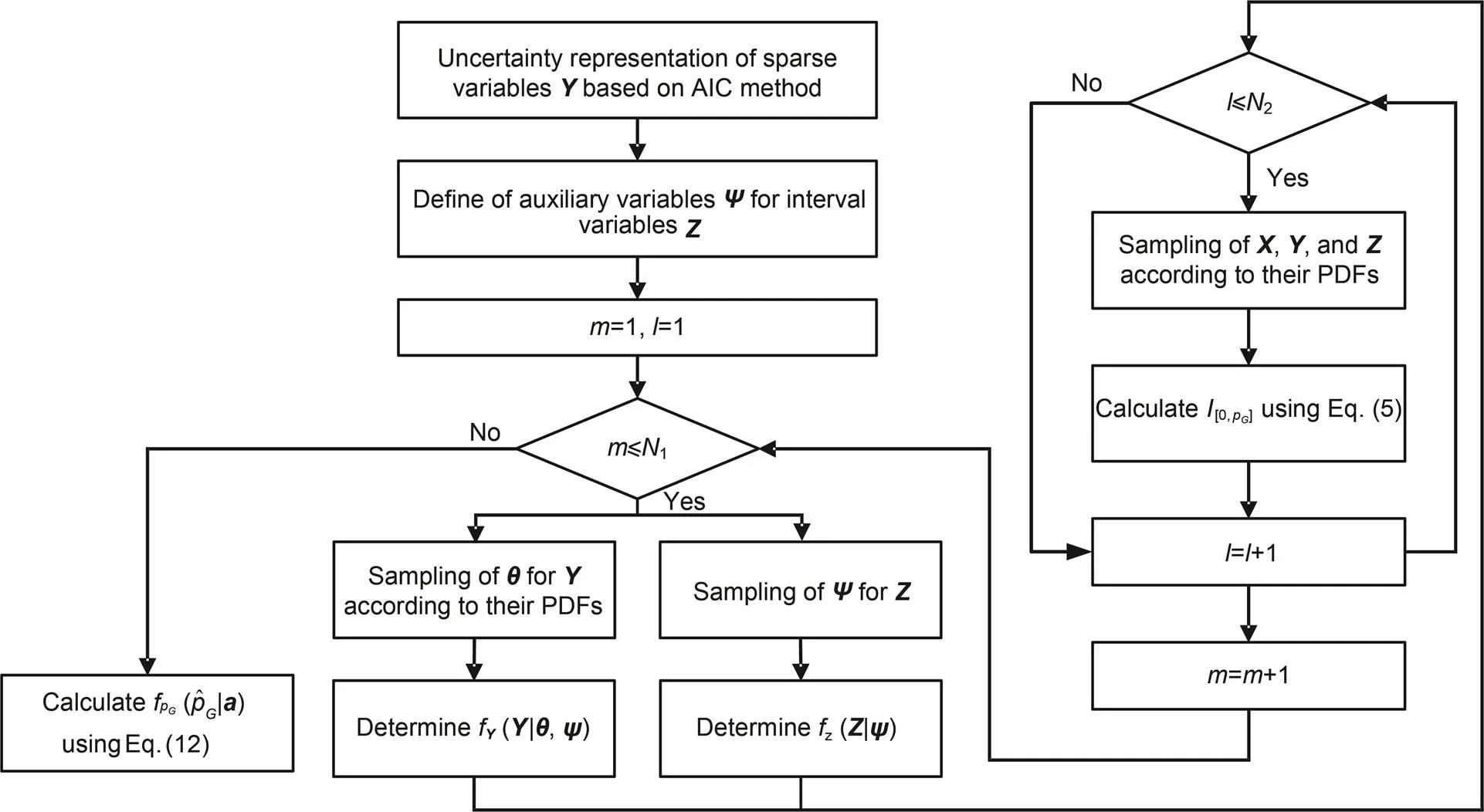
Fig. 2 Calculation flow chart for failure probability. AIC is the Akaike information criterion

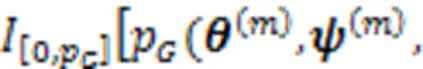
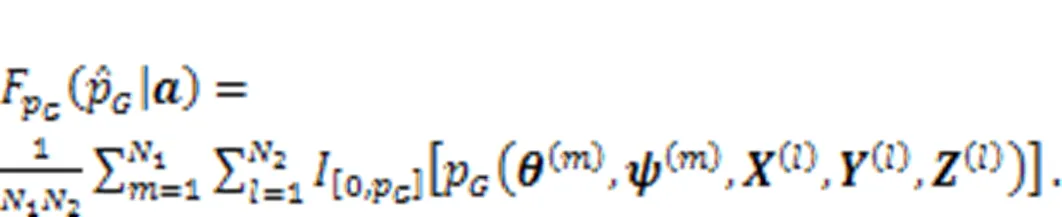
4 Sensitivity analysis of reliability index

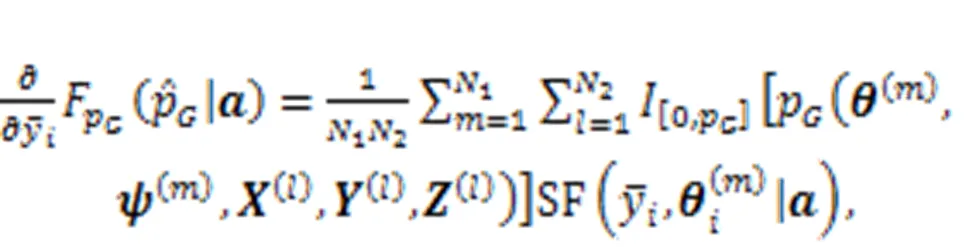
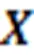
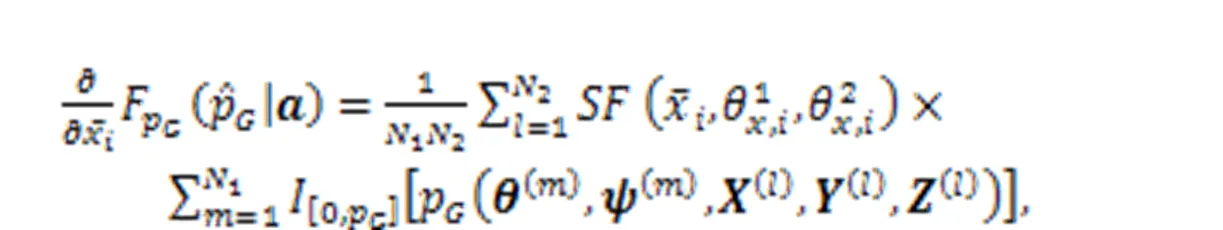
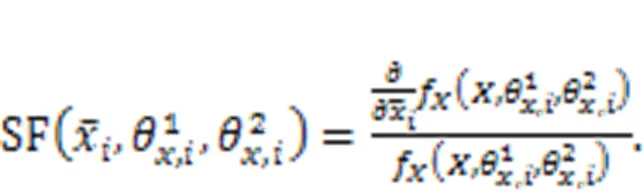
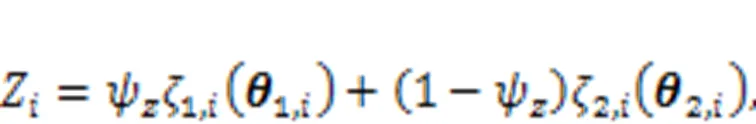
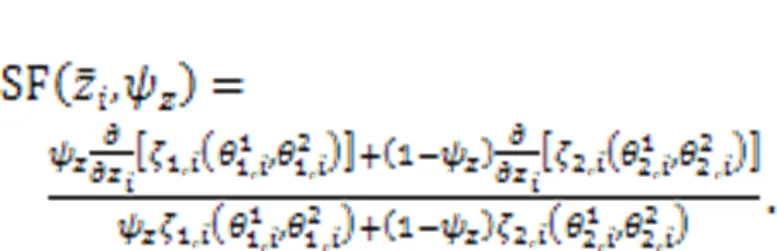
5 Extension of the proposed method to more uncertainty presentation types

The proposed methodology can be extended to the reliability measure of multiple types of epistemic uncertainties, such as-box variables, multi-modal variables, and evidence theory variables.

5.1 p-box uncertainty variables

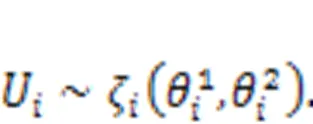
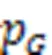
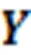
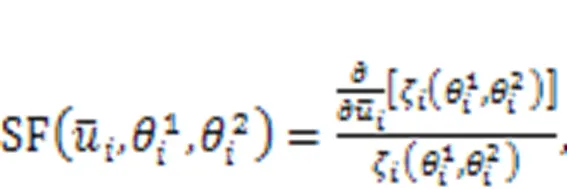
5.2 Multi-modal distribution variables

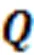
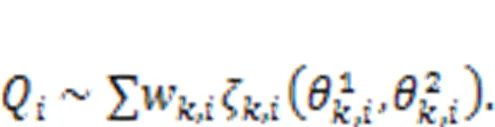
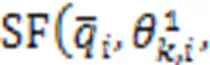
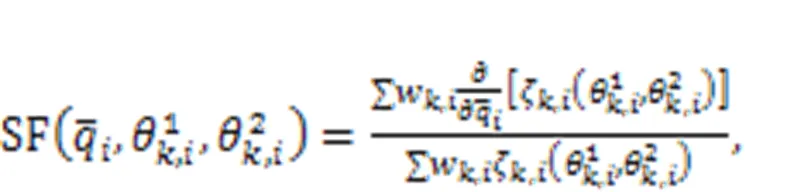
5.3 Evidence theory variables

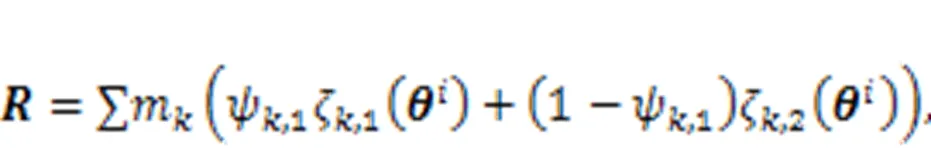
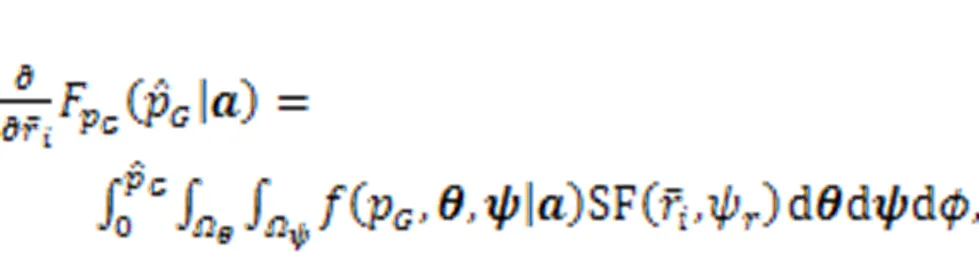
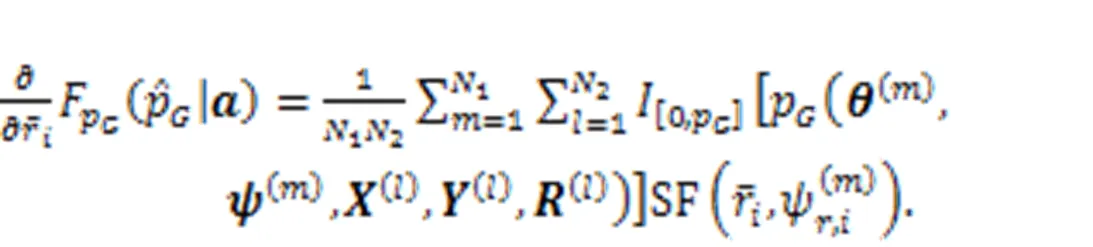
6 Application examples

6.1 Numerical example 1

To demonstrate the effectiveness of the proposed reliability measure approach under insufficient input data, the 2D mathematical performance functions in Eqs. (32)–(34) (Cho et al., 2016a) are introduced.

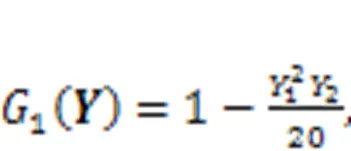
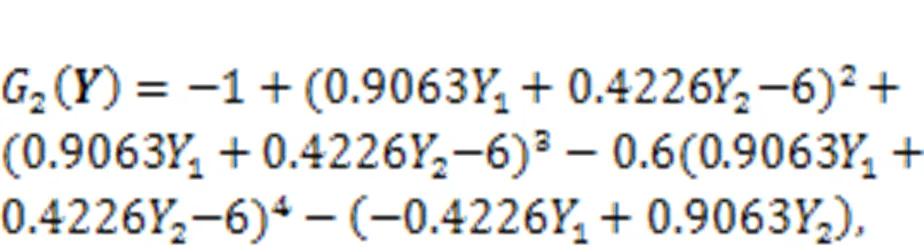
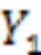
Fig. 3 Conservativeness level of failure probability considering sparse variables: (a) 10 input data; (b) 100 input data

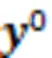
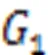
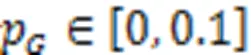
6.2 Numerical example 2

To demonstrate the effectiveness of the proposed reliability measure approach under hybrid uncertainties, the 2D mathematical functions in Section 6.1 are extended to 3D functions in Eqs. (35) and (36).

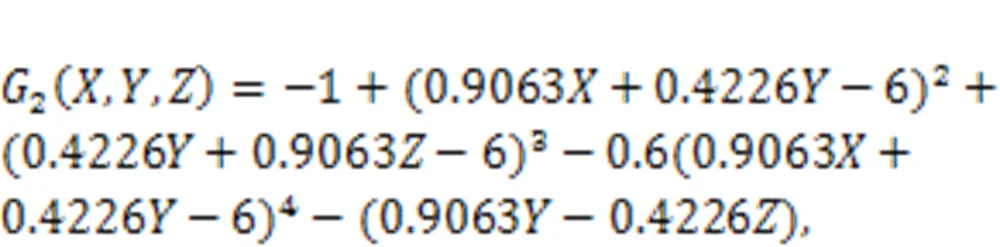
Fig. 4 Sensitivity results under different failure probabilities: (a) ; (b) ; (c) ; (d)

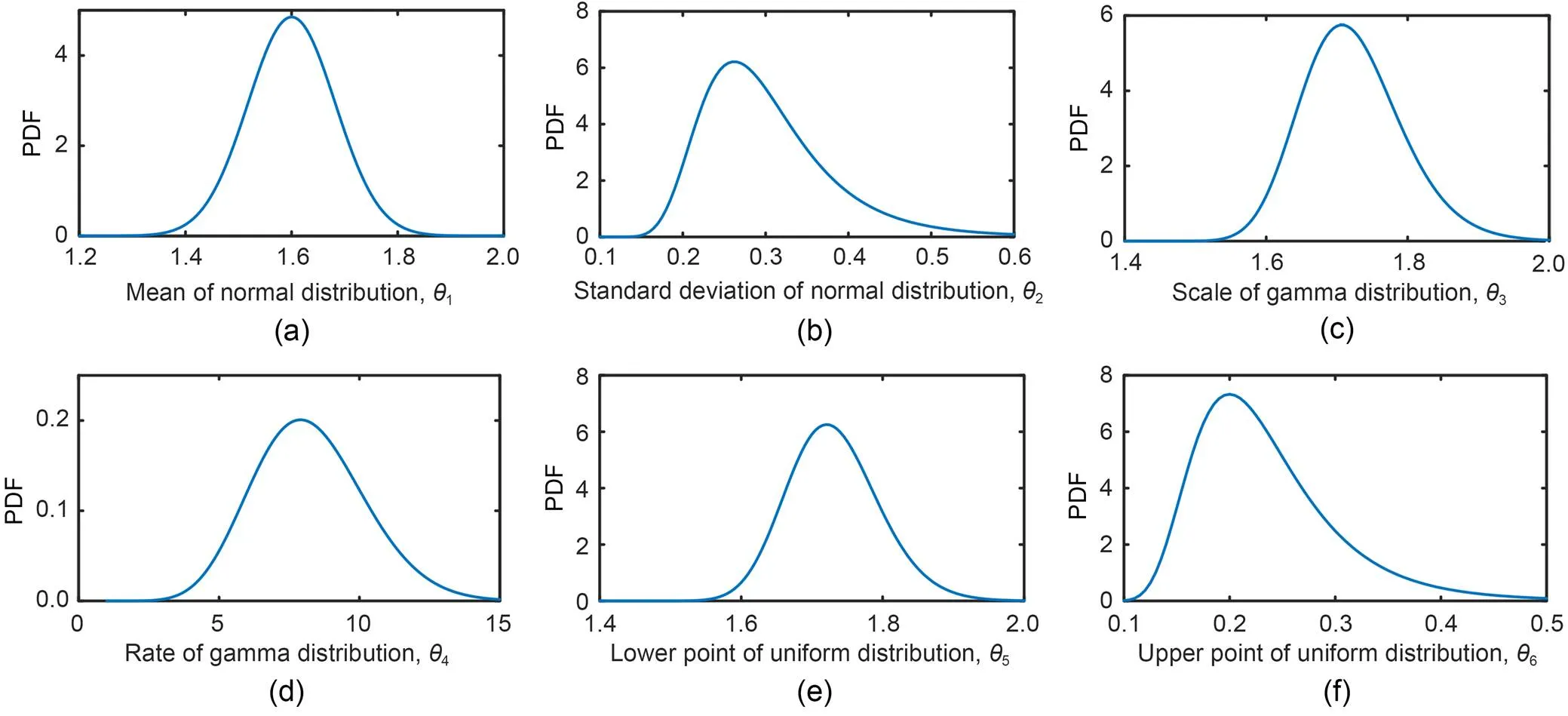
Fig. 5 PDFs of distribution parameters for sparse variable : (a) ; (b) ; (c) ; (d) ; (e) ; (f)

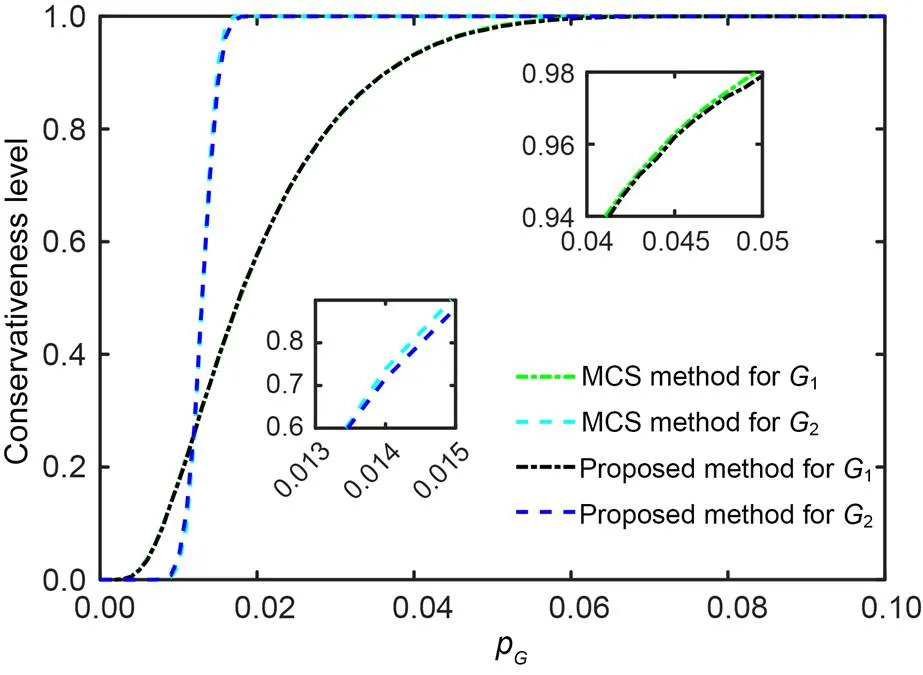
Fig. 6 Conservativeness level of failure probability of proposed method and MCS method

Table 1 Design sensitivity of conservativeness level in example 2

*

6.3 Numerical example 3

To demonstrate the effectiveness of the proposed method in the reliability measure for multiple types of epistemic uncertainties, the numerical example 2 is extended to analysis reliability indices and sensitivity indices considering-box variables, multi-modal variables, and evidence theory variables.

6.3.1Reliability measure considering-box variable

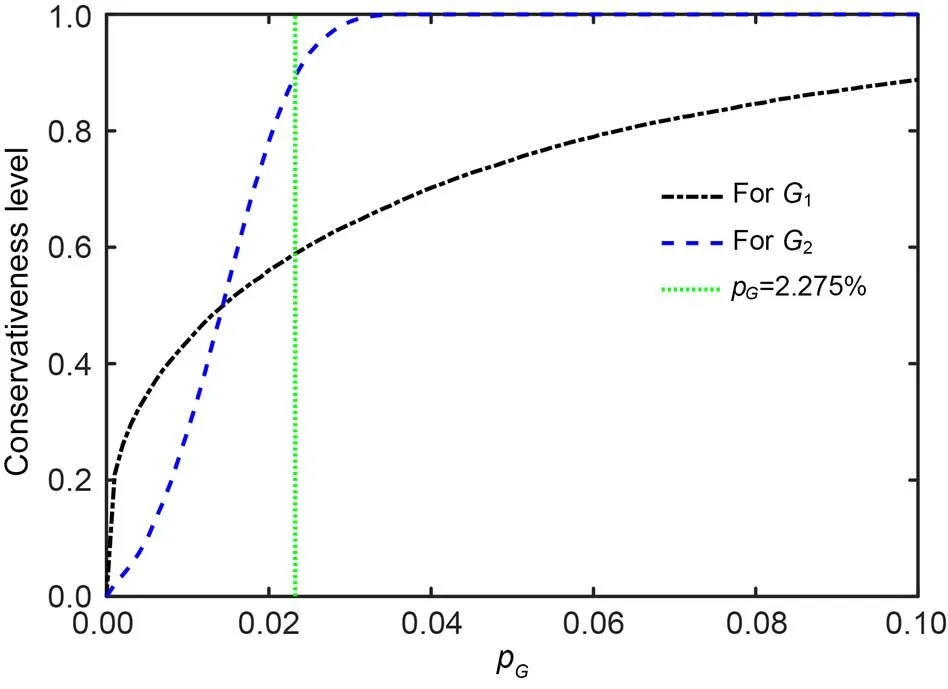
Fig. 7 Reliability result considering p-box variable

6.3.2Reliability measures considering multi-modal variables

Table 2 Design sensitivity of conservativeness level considering the p-box variable

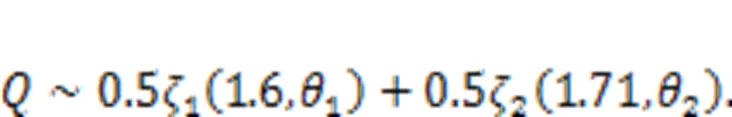
Compared with sparse variable , the weight ratios and distribution types of multi-modal variable are determinate. The failure probability can be calculated using a two-level sampling method for uncertain distribution parameters and design variables, as shown in Fig. 8, which demonstrates that the proposed method can be effectively extended to calculate reliability index considering multi-modal variables.

Table 3 Design sensitivity of conservativeness level considering the multi-modal variable

6.3.3Reliability measure considering evidence theory variable

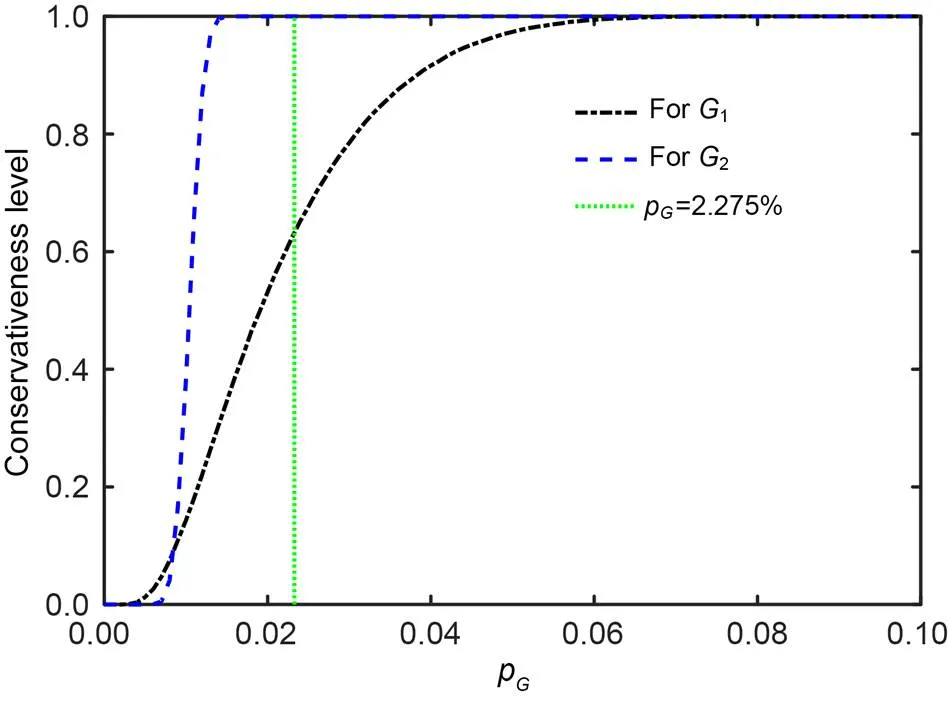
Fig. 9 Reliability measure result considering the evidence theory variable

6.4 Engineering example: forging hydraulic press

The forging hydraulic press is a large piece of equipment, which uses liquid as its working medium, and transfers energy to the forging process, as shown in Fig. 10.

Fig. 11 FEA of the forging hydraulic press: (a) mesh; (b) deformation of the tie rods

Table 4 Design sensitivity of conservativeness level considering the evidence theory variable

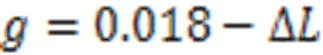
The conservativeness level of failure probability considering hybrid uncertainties is calculated using the proposed method and the MCS method, as shown in Fig. 13. The sensitivity results computed using the proposed method and the FDM are listed in Table 5. These results indicate the proposed method can obtain accurate reliability index and sensitivity results.

7 Conclusions

In this study, a reliability measure approach considering mixture uncertainties under insufficient input data is proposed. First, the sparse variable is represented using weight summation of multiple distribution types based on AIC method under insufficient input data. Second, the failure probability under mixture uncertainties is calculated using the proposed two-level sampling method. Then, a semi-analytical method is proposed to calculate the sensitivity indices of mixture uncertainty variables. Finally, the proposed reliability measure method is extended to deal with-box variables, multi-modal variables, and evidence theory variables.

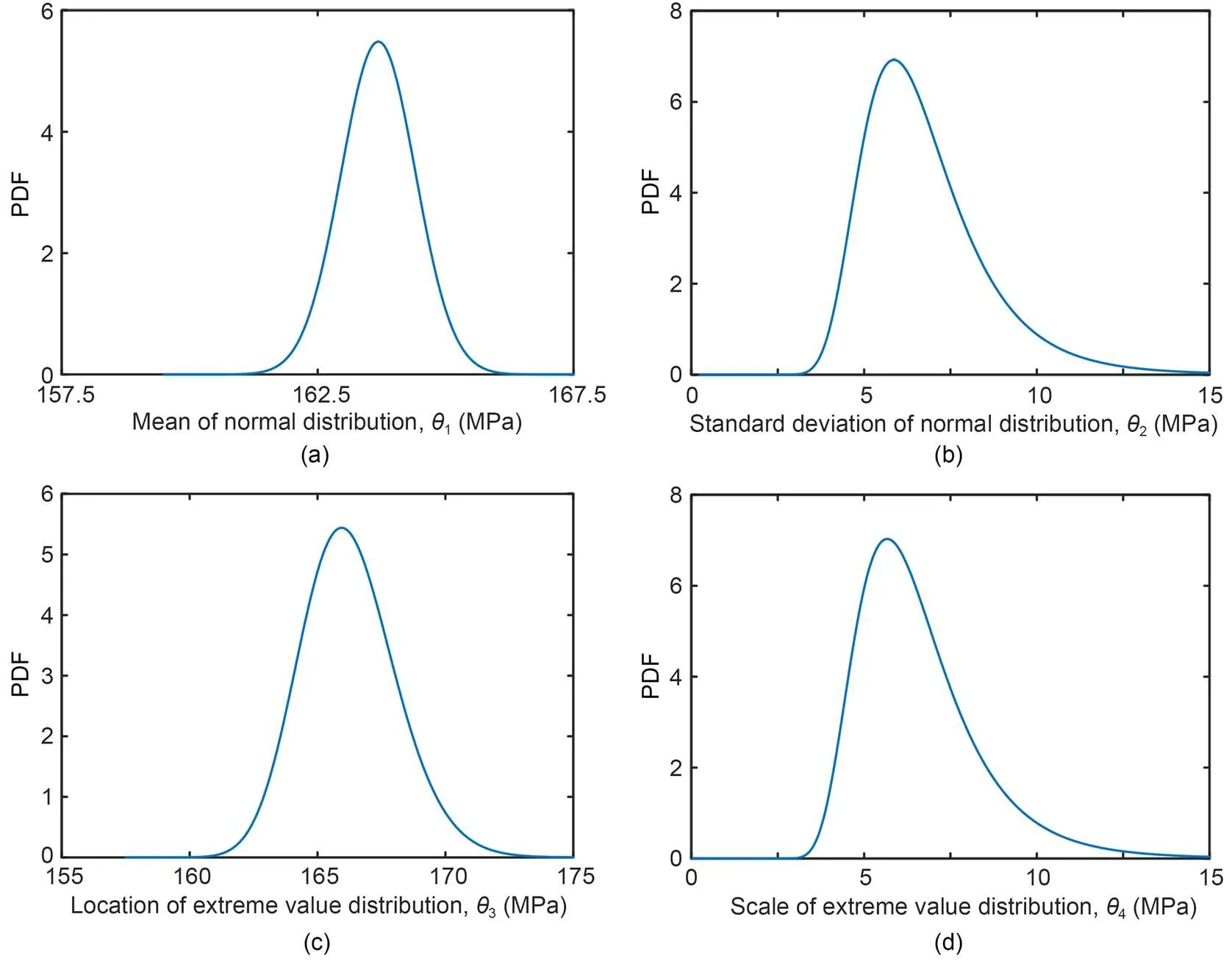
Fig. 12 PDFs of distribution parameters for sparse variable : (a) ; (b) ; (c) ; (d)

From the results of three numerical examples and two engineering examples, the proposed method can obtain accuracy reliability measure results with higher computational efficiency compared with the MCS and FDM methods. Some conclusions are obtained: (i) The proposed method can obtain accuracy reliability measure results with less computational times. The traditional three-level sampling loop for sparse variables is decreased to a two-level sampling loop, which decreases the computation complexity for the reliability measure. (ii) The semi-analytical sensitivity calculation method based on an auxiliary variable method decreases the computational burden, and can be integrated into the uncertainty optimization method with little extra calculation. (iii) The proposed method has been extended to analyze-box variables, multi-modal variables, and evidence theory variables, which can be extended to measure reliability index and sensitivity indices considering more uncertainty types, which is useful for mixture uncertainty optimization design.

Fig. 13 Reliability result of forging hydraulic press

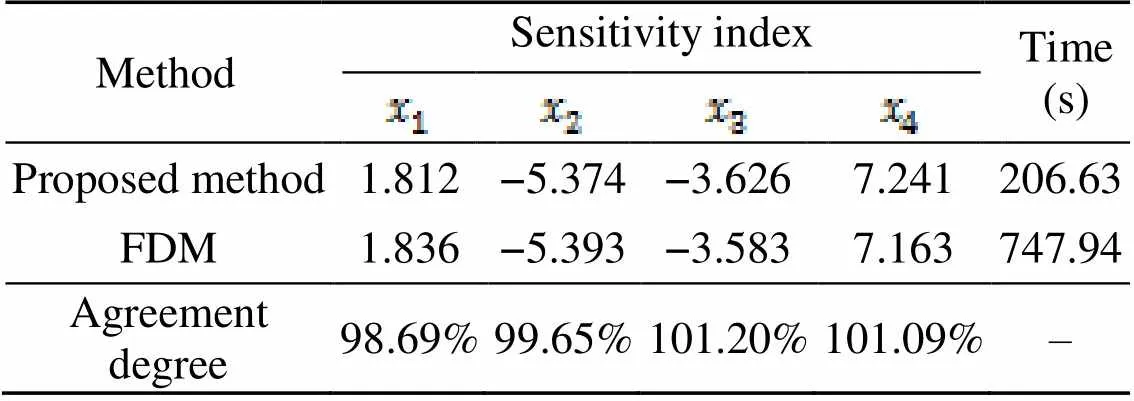
Table 5 Design sensitivity of conservativeness level for forging hydraulic press

This work is supported by the Key Research and Development Program of Zhejiang Province (No. 2021C01008), the National Natural Science Foundation of China (No. 52105279), and the Ningbo Natural Science Foundation of China (No. 2021J163). The authors appreciate the help from Xiang PENG (Zhejiang University of Technology, China) in programming and numerical calculation of distribution types and parameter estimation for sparse variables.

Zhenyu LIU designed the research. Yufeng LYU and Guodong SA derived the mathematical formulas and analyzed the experimental and simulation cases. Yufeng LYU wrote the first draft of the manuscript. Guodong SA was in charge of the whole project. Jianrong TAN gave the theoretical guidance on the whole work.

Zhenyu LIU, Yufeng LYU, Guodong SA, and Jianrong TAN declare that they have no conflict of interest.

Chen JB, Yang JS, Jensen H, 2020. Structural optimization considering dynamic reliability constraints via probability density evolution method and change of probability measure., 62(5):2499-2516. https://doi.org/10.1007/s00158-020-02621-4

Chen WH, Cui J, Fan XY, et al., 2003. Reliability analysis of DOOF for Weibull distribution., 4(4):448-453. https://doi.org/10.1631/jzus.2003.0448

Cho H, Choi KK, Gaul NJ, et al., 2016a. Conservative reliability-based design optimization method with insufficient input data., 54(6):1609-1630. https://doi.org/10.1007/s00158-016-1492-4

Cho H, Choi KK, Lee I, et al., 2016b. Design sensitivity method for sampling-based RBDO with varying standard deviation., 138(1):011405. https://doi.org/10.1115/1.4031829

El Haj AK, Soubra AH, 2021. Improved active learning probabilistic approach for the computation of failure probability., 88:102011. https://doi.org/10.1016/j.strusafe.2020.102011

Faes M, Moens D, 2020. Recent trends in the modeling and quantification of non-probabilistic uncertainty., 27(3):633-671. https://doi.org/10.1007/s11831-019-09327-x

Gan CB, Wang YH, Yang SX, 2018. Nonparametric modeling on random uncertainty and reliability analysis of a dual-span rotor., 19(3):189-202. https://doi.org/10.1631/jzus.A1600340

Hong LX, Li HC, Gao N, et al., 2021. Random and multi-super-ellipsoidal variables hybrid reliability analysis based on a novel active learning Kriging model., 373:113555. https://doi.org/10.1016/j.cma.2020.113555

Kang YJ, Lim OK, Noh Y, 2016. Sequential statistical modeling method for distribution type identification., 54(6):‍1587-1607. https://doi.org/10.1007/s00158-016-1567-2

Keshtegar B, Hao P, 2018. Enhanced single-loop method for efficient reliability-based design optimization with complex constraints., 57(4):1731-1747. https://doi.org/10.1007/s00158-017-1842-x

Lee I, Choi KK, Noh Y, et al., 2011. Sampling-based stochastic sensitivity analysis using score functions for RBDO problems with correlated random variables., 133(2):021003. https://doi.org/10.1115/1.4003186

Lee I, Choi KK, Noh Y, et al., 2013. Comparison study between probabilistic and possibilistic methods for problems under a lack of correlated input statistical information., 47(2):175-189. https://doi.org/10.1007/s00158-012-0833-1

Liu XX, Elishakoff I, 2020. A combined importance sampling and active learning Kriging reliability method for small failure probability with random and correlated interval variables., 82:101875. https://doi.org/10.1016/j.strusafe.2019.101875

Liu Y, Jeong HK, Collette M, 2016. Efficient optimization of reliability-constrained structural design problems including interval uncertainty., 177:1-11. https://doi.org/10.1016/j.compstruc.2016.08.004

Liu ZY, Xu HC, Sa GD, et al., 2022. A comparison of sensitivity indices for tolerance design of a transmission mechanism., 23(7):527-542. https://doi.org/10.1631/jzus.A2100461

McFarland J, DeCarlo E, 2020. A Monte Carlo framework for probabilistic analysis and variance decomposition with distribution parameter uncertainty., 197:106807. https://doi.org/10.1016/j.ress.2020.106807

Ni BY, Jiang C, Huang ZL, 2018. Discussions on non-probabilistic convex modelling for uncertain problems., 59:54-85. https://doi.org/10.1016/j.apm.2018.01.026

Oberkampf WL, Helton JC, Joslyn CA, et al., 2004. Challenge problems: uncertainty in system response given uncertain parameters., 85(1-3): 11-19. https://doi.org/10.1016/j.ress.2004.03.002

Peng X, Li JQ, Jiang SF, 2017. Unified uncertainty representation and quantification based on insufficient input data., 56(6):‍‍‍1305-1317. https://doi.org/10.1007/s00158-017-1722-4

Sankararaman S, Mahadevan S, 2013. Distribution type uncertainty due to sparse and imprecise data., 37(1-2):182-198. https://doi.org/10.1016/j.ymssp.2012.07.008

Sankararaman S, Mahadevan S, 2015. Integration of model verification, validation, and calibration for uncertainty quantification in engineering systems., 138:194-209. https://doi.org/10.1016/j.ress.2015.01.023

Solazzi L, 2022. Reliability evaluation of critical local buckling load on the thin walled cylindrical shell made of composite material., 284:115163. https://doi.org/10.1016/j.compstruct.2021.115163

Tostado-Véliz M, Icaza-Alvarez D, Jurado F, 2021. A novel methodology for optimal sizing photovoltaic-battery systems in smart homes considering grid outages and demand response., 170:884-896. https://doi.org/10.1016/j.renene.2021.02.006

Tostado-Véliz M, Kamel S, Aymen F, et al., 2022. A stochastic-IGDT model for energy management in isolated micro grids considering failures and demand response., 317:119162. https://doi.org/10.1016/j.apenergy.2022.119162

Wakjira TG, Ibrahim M, Ebead U, et al., 2022. Explainable machine learning model and reliability analysis for flexural capacity prediction of RC beams strengthened in flexure with FRCM., 255:113903. https://doi.org/10.1016/j.engstruct.2022.113903

Wang C, Li QW, Pang L, et al., 2016. Estimating the time-dependent reliability of aging structures in the presence of incomplete deterioration information., 17(9):677-688. https://doi.org/10.1631/jzus.A1500342

Wei PF, Song JW, Bi SF, et al., 2019. Non-intrusive stochastic analysis with parameterized imprecise probability models: II. Reliability and rare events analysis., 126:227-247. https://doi.org/10.1016/j.ymssp.2019.02.015

Yun WY, Lu ZZ, Jiang X, et al., 2020. AK-ARBIS: an improved AK-MCS based on the adaptive radial-based importance sampling for small failure probability., 82:101891. https://doi.org/10.1016/j.strusafe.2019.101891

Zhang Z, Wang J, Jiang C, et al., 2019. A new uncertainty propagation method considering multimodal probability density functions., 60(5):1983-1999. https://doi.org/10.1007/s00158-019-02301-y

Zhao YG, Zhang XY, Lu ZH, 2018. Complete monotonic expression of the fourth-moment normal transformation for structural reliability., 196:186-199.https://doi.org/10.1016/j.compstruc.2017.11.006

Sections S1‍–S4

June 6, 2022;

Revision accepted Sept. 20, 2022;

Crosschecked Jan. 1, 2023

© Zhejiang University Press 2023