基于频率的索力测量方法研究

2023-02-15赵震寅

水利技术监督 2023年1期

赵震寅

(浙江理工大学建筑工程学院，浙江杭州 310018)

拉索索力测量方法主要包括：千斤顶油压表读数法、压力传感器测试法、磁通量测试法及振动频率测试法。

在各类测量方法中，千斤顶油压表读数法和压力传感器测试法仅可用于施工阶段拉索张拉时的监测，无法用于成桥阶段的索力检测。而相较于前述测量方法，频率法能够灵活运用于各阶段的桥梁索力检测，在操作便捷的同时也保证了精度，拥有较为完备的测量体系，目前绝大多数工程都倾向于采用频率法对桥梁进行索力检测。

但在实际测量索力的过程中，频率法使用的因素有多方面影响，包括拉索的抗弯刚度、边界条件、计算长度、垂度以及测量温度，频率法发展至今诞生了诸多基于影响因素的索力计算理论和修正方法。鉴于上述情况，本文梳理了现有频率法测量索力的研究进展，着重论述了各研究成果的优化原理，指明了各自的优点和局限性，归纳了不同方法的适用条件，并展望了频率法在今后的研究趋势。

1 频率法索力测量原理

处于工作状态的拉索会在诸如环境因素或人工激励作用下发生微小振动，通过使用高分辨率的频率传感器以及对应的数据采集设备，可获得拉索振动时的若干阶自振频率。再结合索力与拉索线密度、索长、自振频率、边界条件、抗弯刚度等的关系式得出拉索索力[1]。拉索索力计算公式基于以下假设：

(1)拉索垂跨比很小，不考虑垂度的影响；

(2)拉索只在竖向平面内振动，忽略水平方向的移动，且竖直方向的运动也是微小的；

(3)拉索的几何形状近似用抛物线表示[2]。

如图1所示，取拉索任意一段微小长度作为微元体，其平衡方程如下：

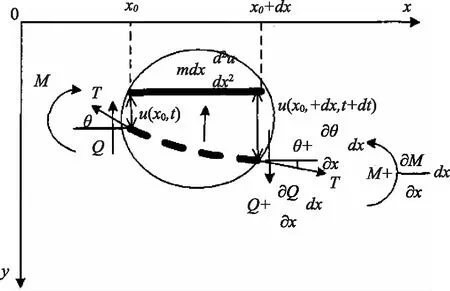
图1 拉索微元体受力图

(1)

(2)

式中，Q—剪力，N；M—弯矩，N·mm—拉力，N；u—y方向上的位移，mm。

根据梁弯矩和中和轴弯曲的曲率关系整理公式(1)和(2)可得到振动微分方程：

(3)

方程的解为：

u(x,t)=u(x)·y(t)

(4)

通过采取离散变量法最终可得到如下关系式：

y(t)=A1sinωt+A2cosωt

(5)

u(x)=Asinαx+Bcosαx+Csinhβx+Dcoshβx

(6)

式中，y(t)—时间函数；u(x)—振型函数；A、B、C、D—根据边界条件确定的待定系数；ω—拉索的自振圆频率，rad/s。其中：

(7)

式中，m—拉索单位长度质量，kg/m；T—拉索索力，N；EI—拉索的抗弯刚度，N·mm2。

上述推导过程采用了两端铰接的拉索模型，为满足一般边界条件的设定，在现有铰接的基础上，再在两端支座处各添加一个弹簧约束，以此作为最终的力学模型。假定两端弹簧铰的约束刚度相同，k为弹性嵌固系数。此时拉索的边界条件为：

(8)

将(8)代入方程(6)中，通过行列式运算和简化最终得到了一般边界条件下的拉索索力关于自振频率的表达式：

k2[2αβ(1-cosαLcoshβL)+(α2-β2)
sinαLsinhβL]+2kEI(α3cosαLsinhβL-
α2βsinαLcoshβL+αβ2cosαLsinhβL-β3sinαLcoshβL)
-(EL)2(α2+β2)sinαLsinβL=0

(9)

由于上式的求解较为困难，在实测中缺乏便捷性，因此理论上只考虑简支边界的情况，并逐步发展成了最为通用的拉索索力计算理论，即张拉弦理论。

张拉弦理论在支座处仅考虑铰接情况，拉索不受转动约束，此时k=0，代入方程(9)中，并结合式(3)可得到索力的表达式：

(10)

式中，L—拉索的计算长度，m；fn—拉索第n阶自振频率，Hz；n—振动阶数。

当忽略抗弯刚度时，公式则转变为：

(11)

式(10)最先由Irvin[3]提出，是基于简支理论推导的拉索索力计算公式，考虑抗弯刚度EI的影响，多用于短索索力计算，也是最基础的索力计算模型；式(11)是实际运用最广泛的经典索力计算公式，因其不考虑抗弯刚度，该状态下的拉索为柔性，所以往往用于细长索的索力计算，结果也较为准确，计算过程多采用拉索的低阶振频。

从推导过程能够看出，经典索力计算公式是建立在简支边界条件下的，但是实际拉索的边界条件多处于简支和固支之间，亦或是完全固支，直接将该公式运用于所有类型拉索的索力计算中难免会造成误差，另外计算长度L的取值准确程度也会影响到计算结果，拉索自身的抗弯刚度、垂度以及所处环境的温度都会直接影响到索的振动频率fn，进而影响索力，因此有多项研究探讨了上述因素在频率法中的影响。

2 应用中的修正

2.1 边界条件影响

在索体系的桥梁当中，拉索的连接方式主要有销栓式和承压式，两类连接方式的共同点为各自端部至少有一侧可等效为固支，因此必须考虑边界条件对索力的影响，固支梁理论便是对这一构造特性的论证。

Zui[2]提出的固支梁理论就是在方程(9)中考虑k=∞的情况，此时拉索的转动约束被视作无穷大，可将边界条件视作固支。

为方便计算，在此过程中引入了参数ξ和C。

(12)

(13)

ζ为无量纲参数，也称作拉弯比，用于表示拉索的动力特性与张紧弦的接近程度，取值越大接近程度越高，抗弯刚度影响也越小。

根据ξ取值范围的不同和所测得的拉索不同阶振动频率，Zui等[2]通过曲线拟合的方法得出了拉索索力-振频的关系式：

(1)采用一阶振型频率计算时：

(14)

(2)采用二阶振型频率计算时：

(15)

(3)采用高阶(三阶及以上)振型频率计算时：

(16)

上述固支梁理论为后续索力公式的改进提供了依据，国内学者也提出了众多基于固支梁理论下考虑拉索边界条件的索力计算公式：

任伟新等[4]采用能量法和曲线拟合，建立了分别考虑索垂度和抗弯刚度影响由基频计算索力的公式：

(17)

陈淮等[5]采用数值计算和曲线拟合，推导出了考虑吊索抗弯刚度和吊索两端边界条件影响的索力计算公式：

(1)采用一阶振型频率计算时：

(18)

(2)采用三阶振型频率计算时：

(19)

安振源等[6]使用迭代法和曲线拟合方法，建立了索力与一阶振动频率的关系式：

(20)

以上代表性理论皆是基于两端固支的边界条件考虑的，一定程度上弥补了早期国内索力计算领域的空白，虽然顾及了边界条件但缺陷也是明显的，例如边界条件的定义存仍在理想化情况，采用高阶频率计算时精度难以把控，公式运用也并非十分方便。

为了提高频率法公式的便捷性，甘泉[7]采用了将固支欧拉梁的振型函数作为两端固接的振型函数：

φn(x)=[cosh(ax)-cos(ax)]-
En[sinh(ax)-sin(ax)]

(21)

(22)

根据上述条件研究建立了一套较为便捷的可用于固支和简支边界的拉索索力计算公式，相较于经典固支梁理论的振型函数，采用欧拉梁振型函数可降低公式的复杂程度，但所基于的边界条件仍为固支。

对于实际服役的桥梁而言，拉索边界条件多介于铰支和固支之间，拉索端部或多或少会受到抗弯刚度影响，而技术人员在计算拉索索力时习惯于考虑单一的边界状态，由此必将造成检测结果的偏差。

刘文峰等[8]从拉索实际的边界条件出发，提出了固支和简支耦合形式的振型函数：

(23)

(24)

式中，r—振型的阶数；l—拉索计算长度，m；k—固支振动和简支振动的一个比值，其大小代表了固支在边界中所占的比重，可在后续求解索力的过程中求得。研究最终基于耦合边界形式的振型函数给出了拉索索力-刚度关系式，方法较好地考虑了拉索实际的端部情况，精度优良，但计算过程仍略显复杂。

孙永明等[9]在指出工程实际拉索与理想匀质拉索模型区别的基础上，研究了端部性质对频率法的影响，并最终建立了可计入端部性质影响的修正索力计算公式：

(25)

2.2 抗弯刚度影响

抗弯刚度对索力的影响主要体现在索长较短或索径较大的拉索上。从构造角度出发，拉索是由数根平行的钢筋、钢丝或钢绞线经小角度扭绞形成。若拉索的钢丝之间完全滑移，则拉索惯性矩就是各根钢丝的惯性矩之和；若拉索的钢丝之间完全粘结，即各根钢丝形成了一个整体，则索的惯性矩为等截面钢棒的惯性矩，两种假设的结果相差较大。而实际工程中拉索内部构造往往介于彼此分离和完全粘结之间，严格意义上来说拉索的抗弯刚度是一个未知量。

苏成等[10]采用有限元法及样条拟合技术获取了拉索索力与频率的对应关系，提出一种基于多阶频率测试结果的斜拉索抗弯刚度识别方法，通过实测数据分析得出了拉索的实际抗弯刚度为0.37(EI)max,其中(EI)max为索按全截面计算时的抗弯刚度。

但是实际拉索的抗弯刚度并不是一个恒定的值，会因其他参数的改变而发生细微的变化，例如索力和温度，因此在探寻抗弯刚度对索力影响的过程中，不少学者另辟蹊径，提出了一种避开抗弯刚度求算索力的思路，如孟少平等[11]运用能量方法建立了索力、抗弯刚度和固有圆频率之间的关系：

(26)

式中，φ(x)—振型函数，通过建立一端铰支一端固支的振型函数，配合联立1阶和2阶固有圆频率的表达式ω1和ω2，可消去抗弯刚度EI，并最终得到索力关于前两阶固有振频的计算式：

(27)

上式将抗弯刚度作为隐式参数计算，回避了工程中拉索抗弯刚度难以识别的问题，在无法精确获取抗弯刚度的情况下优势显著；同样，袁博等[12]也利用能量法，提出了在拉索抗弯刚度未知的情况下，用于计算拉索索力的计算方法；Seyed等[13]在推导考虑刚度影响的索力计算公式时也选择了规避抗弯刚度的方法，但采用的原理并非能量法，首先计算拉索实测频率和计算频率间的差值，将该差值定义为关于刚度EI和索力H的误差函数E，再通过E求得一阶固有振动频率后，即可计算出索力。

当不考虑规避抗弯刚度时，Chen等[14]通过对一系列缆索进行抗弯刚度实验后得出结论，缆索的抗弯刚度会随着索两端张拉力的增大而增大；而张永平等[15]进一步提出缆索抗弯刚度与拉力的非线性关系模型：

ω2=n2π2T/mL2+n4π4EI/mL2

(28)

式中，ω—缆索的振动频率，Hz；n—振频阶数。上式可用于频率法中拉索抗弯刚度的修正，但仍需针对不同的边界条件进行更深入的研究，完善抗弯刚度的修正模型。

燕启清等[16]建立了一种考虑短吊杆抗弯刚度的索力计算公式：

(29)

(30)

(31)

式中，f1—吊杆一阶振动频率，Hz；TQ—标定吊杆索力比例系数时的千斤顶张拉力，N；Tb—第一次张拉阶段吊杆张拉力设计值，N；Ts—成桥后吊杆索力设计值，N；λ—吊杆边界条件修正系数；C—吊杆横向抗弯刚度修正值；K—吊杆索力比例系数；η—吊杆索力偏差系数。

η=1-Tb(Ts+C)/Ts(Tb+C)

(32)

当|η|≤Δ时，可不考虑吊杆横向抗弯刚度对索力的影响；当|η|≥Δ时，必须用式(32)进行索力修正，此时将被修正的吊杆定义为短吊杆，横向抗弯刚度对索力的影响不可忽略，Δ的值则根据相应的技术规范取定。

2.3 计算长度

有关拉索计算长度的研究本质上是由边界条件引申而出的一类子问题，由于边界刚度的存在，在计算拉索索力时无法取整段索长作为实际的计算长度，取值的关键在于精确判别端部抗弯刚度限制拉索有效振动的范围。

拉索通常是由：套筒、锚杯、中部自由振动的索体3部分组成，如图2所示。锚固区域具备较大的刚度，能够有效限制振动，但是其限制自由部分振动的能力不显著，在索力计算时索长可取拉索能振动部分的长度，设计文件中一般为拉索两端锚垫板之间的距离[17]。陈阳[18]通过采用牛顿切线法迭代计算有效长度的方法，得出吊索计算长度可取为上下锚固点之间的理论长度，验证了设计规范中的内容，但是其实验对象为9～38m的吊杆，且实测数据表明索力误差可达8%，精度尚待提高。而且在长度更大或是具有一定垂度的拉索有效长度取值中该方法或许并不适用。

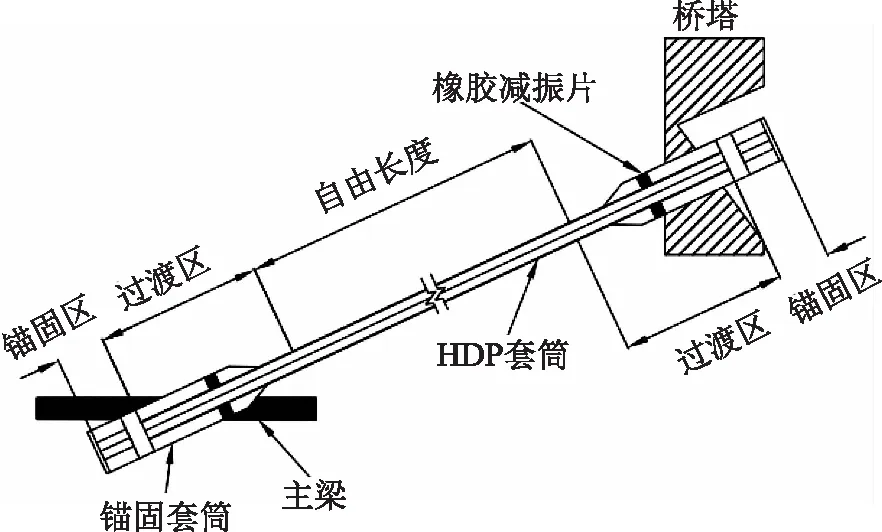
图2 拉索构造示意图

经有关学者实验分析得出，拉索有效长度取值的精确程度对长索的影响较小，但对短索的影响较大，有数据表明误差最高可达66%[19]，这就意味着在面对短索索力的计算时要更为严格地取定拉索有效振动长度。

宋一凡和贺拴海[20]引入了动力计算长度的概念，解决了用振动法测估索力时面临的有效索长取值难题，提出了基于二阶固有频率的动力计算长度lde的实用公式：

(33)

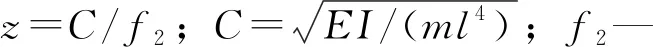
为减缓拉索振动，保证桥梁整体的稳定性，在实际布置拉索时一般会在套筒内安装减振片等阻尼装置，或是在外部安装减振器。减振器的设置会缩短拉索的自由振动长度因此需重新定义有效长度，胡利平和林育洪[21]采用的方法是分别测取拉索安装减振器前后的频率，再利用2次频率值的不同来换算索长：

(34)

式中，l′—换算后的索长，m；l—实际索长，m；fn、f′n—安装减振器前后的某一阶拉索振动频率，Hz，一般可取基频。假如事先没有进行该项操作，则可先取拉索上下减振器之间的长度作为计算长度再适当估计结果误差范围进行调整的办法。相较于其他理论，采用此方法的分析结果较快捷，具备一定的工程推广性，但并没有针对不同边界条件的拉索进行公式的细化，在使用过程中也难免会产生误差；林天然[22]在采用张拉弦理论计算索力的基础上提出用吊杆计算长度的修正值对索力进行修正，通过对某一大跨度拱桥吊杆进行索力测试，最终确定修正值为减振器到锚固端距离的0.9～1.1倍之间，该法同样是一种快捷的计算长度修正手段，但在特殊情况下也同样面临着精度不足的问题。

Li[23]根据能量法发展了一种基于附加质量块的有效长度确定方法，得到了固有频率和有效长度间存在的解析关系：

(35)

式中，ω1、ωm1—施加质量块前后拉索的一阶固有振频，Hz；m—拉索的单位长度质量，kg；M—质量块的质量，kg。Li将该公式运用于某吊杆拱桥的索力检测中，通过与实测值进行比对显示此方法可将索力误差控制在5%，在短索中的预测精度表现较为出色。

当面对具有一定垂度的长拉索时，基于抛物线理论的长度计算法是设计中普遍采用并且认可度较高的方法，但随着拉索长度的增加，垂度的非线性影响会不断增大，传统抛物线理论的计算精度会因此受到影响，考虑到这一问题，孟庆成等[24]提出采用悬链线公式来计算斜拉索的无应力长度，长度的计算公式为：

l0=l-Δl

(36)

(37)

(38)

式中，l0—拉索无应力长度，m；H1—拉索下锚点拉力的水平分量，N；gcb—拉索的单位长度重量，kg/m；a—上下锚点之间的水平距离，m；λ1—下锚点处拉索切线与水平的夹角。实测结果显示，该公式下的各阶频率估算的索力波动较小，改进了用抛物线法近似求解索长的传统方法，可用于大跨度桥梁的拉索计算中。

除上述理论外，学者们在研究过的程中也建立了众多从不同原理出发的，关于计算拉索有效长度的实用公式。周正茂[25]提出了振型节点法，利用3阶以上模态振型的中间节点间距作为计算长度，该方法的优点在于回避了复杂的边界条件，原理简洁思路新颖，可直接运用于公式(10)中，以三阶模态为例，选取三阶模态频率f3作为计算频率，取中间相邻2个模态节点间的距离作为计算长度L，因为此时只取了一段距离，所以阶数n取为1，在更高阶模态中n可取2或更大，L也要进行相应调整。方法的不足之处在于其精度易受索长、振型阶次和边界条件的影响，仍有很大的改进空间。

史杰[26]通过建立静载试验前后吊杆索力差和频率差的解析式，反推得出了索力计算长度的表达式：

(39)

其中：

(40)

(41)

式中，n—振动阶数；ρ—拉索线密度，kg/m；δT—加载前后索力的增量，N；fn,1、fn,2—加载前后对应的n阶振动频率，Hz。由公式(41)可知索力增量和频率平方差成正比，因此Kn可通过拉索加载前后的索力增量和频率数据拟合得到。此方法原理简单，操作步骤简洁，可运用于新旧桥梁的索力检测。

2.4 垂度影响

实际许多的桥梁拉索会呈现出下垂的状态，呈现出很强的非线性性质[27]。拉索垂度的成因包括：索力、索长、自重、倾角等，垂度的存在对拉索的最直接影响就是其振动频率。在拉索长度确定的前提下，拉索垂度对基频的影响较大，但是对高阶频率(四阶及以上)的影响较小。

早期的研究例如岛田忠幸[28]通过引入参数Γ来量化拉索垂度对固有频率的影响：

(42)

Irvine[3]通过推导微元体平衡方程，提出了用无量纲参数λ2考虑拉索垂度对索力的影响，该参数也成为了拉索弦振动理论中的基本参数之一：

(43)

(44)

参数λ2反映的是索的垂度和弹性模量对基频的影响，具体表现为当λ2较大时，索力较小，拉索的垂度较大，对基频的影响也较大，反之则越小。

由于直接采用λ2求解无法解得特定垂度下索力与振动基频的关系式，因此往往用能量法近似来实现这一目标，得到的考虑垂度的索力-基频的关系式如下：

(45)

式中，ω—拉索振动的基频，Hz；H—索力的弦向分量，N；l—拉索计算长度，m；m—拉索单位长度质量，kg/m。最终可以得出考虑索垂度和弹性影响的索力计算实用公式[29]：

(46)

上述公式在行业方面的认可度高且较为基础，但在拉索振型的考虑上存在局限，只是给出了基于基频的索力公式，并未考虑拉索垂度对更高阶振动频率的影响。

李国强等[30]通过验证各因素对索力检测的影响得出结论：垂度只影响索的奇数阶振频，尤其反映在一阶频率上，对高次奇数阶频率的影响较小，对偶数阶频率的影响可忽略不计。在涉及垂度作用下的拉索频率选取中，该结论有着重要的参考价值。

同样，在处理垂度对不同阶频率的影响时，冉志红和李乔[31]通过采用奇异摄动解法这一种求解微分方程近似解析解的方法来求解拉索的动力平衡方程，给出了考虑拉索垂度影响的索力计算公式：

(47)

其中：

(48)

刘志军[32]在研究用垂度修正索力的过程中，提出了采用传递矩阵法考虑垂度对拉索索力的影响，该方法基于拉索的微元体静力平衡方程，将拉索分为了n+2个质点和n+1个没有质量只有张力的弦，建立了求解索力的矩阵方程，方程的关键点在于修正垂度影响下的拉索自振频率，进而使得索力预测的结果更加准确。传递矩阵法易于编程且精度可靠，在实际工程中具备快速测量的优势。

相较于用垂度修正索力，运用拉索垂度特性反求索力也是一条新思路，葛俊颖等[33]通过有限元软件分析证明了当斜拉索的索力较大时，其拉索中部位置的索力和垂度存在着确定的函数关系，且不受拉索本身刚度和两端支承条件的影响。当选取一定长度的中间索段时索力的计算公式为：

(49)

式中，TM—该索段的平均索力，N；T0—最小索力，N；TL—最大索力，N，分别位于该段的最上端和最下端；L—索段的索长，m；α—对应的倾角；fmax—最大垂度，后3项参数可由仪器测得，最后根据该段拉索的各项索力可确定整条拉索的索力情况，选取的索长越大结果越精确，且不受抗弯刚度和边界条件的影响。

2.5 测量温度影响

从拉索自身温度效应出发，拉索长度会随材料的热胀冷缩而产生细微的改变，从而造成索力和频率的变化；整体上，桥梁拉索通常由钢材制作而成，与之锚固的主梁则大多为混凝土构件，材料间不同的膨胀系数决定了二者在同温度变化下的变形存在差异，变形速率也不同，整体结构的部分变形不一致也导致了索力随温度的变化，而实际的情况更为复杂，桥梁的温度日变化幅度呈现出：气温>拉索温度>梁、主塔温度的梯度状况，这使得索力关于温度的变化值变得更难以捕捉。

一座桥梁在正常的大气环境中会经历酷暑和严寒，年温差通常会超过50℃。温差会对频率造成影响进而影响索力，同时也会对垂度造成影响，所以拉索的索力、垂度、振动频率、环境温度之间的关系是复杂的，关键就在于能否将温度的影响准确量化，因此国外学者Kim[34]和Park[35]开始尝试一种能够结合更复杂因素的参数敏感性方法(PSM)来识别多因素影响下的索力。

国内方面，候俊明[36]曾对某一单索面斜拉桥进行索力监测，实测结果显示拉索索力会随着温度而异，在室外时隔4h的索力变化幅度可达到2.5%，由此可见温度对于索力的影响不可忽略。但研究并没有给出基于温度变化的索力计算公式或修正方法，同时缺少了温度对其他结构参数影响的讨论。任远[37]尝试用限元模型对拉索进行温度效应的监测，虽然能够有效反映索力的变化趋势，但在施工控制中只能作为一种近似的手段。

在获取了索力随温度变化趋势的前提下，Chen[38]采用总体经验模态分解法(EMD)对索力、环境温度、索温变化量的时域图进行时程分析，研究了基于环境气温和拉索索温变化量的索力修正系统，并在EMD的基础上更进了一种基于噪声辅助的数据分析方法(EEMD)，方法取得了显著的效果，较大程度地消除了拉索的温度效应，但该技术的难度较大且局限于低塔斜拉桥的桥型，目前仍位于改进阶段。

考虑到需要建立一种可供现场快速使用的公式方法，Ma等[39]采用有限差分法来处理拉索动力方程中温度的影响，并最终求得了索力关于温度变化的数值解，但是公式仍较复杂；艾玉麒[40]提出了一种基于温度的索力变化量公式：

ΔT1=KαEA(t1-t)

(50)

式中，K—温度修正系数，可由相应的有限元模型计算得到；α—线膨胀系数；t1—实时温度，℃；t—设计温度，℃。对比文献[39]的公式，该方法原理简明且相关参数易被采集，在涉及温度的索力修正中其运用更加便捷。