夏存言，张 刚，耿云海，周斯腾

(1.哈尔滨工业大学航天学院卫星技术研究所，哈尔滨 150080；2.哈尔滨工业大学航天学院，哈尔滨 150001)

0 引 言

随着航天事业的发展，航天任务的多样性和复杂度都日渐增加。在众多的航天任务中，航天器轨道设计和轨道确定问题对于任务规划、在轨跟踪等环节都是十分重要的研究内容。同时，随着航天器的低成本化和小型化，越来越多的航天任务不再是由单独的一个航天器来完成，而是多航天器共同实现任务目标。此类任务中，航天器之间往往是近距离飞行，其相互状态往往比其自身在惯性空间内的飞行状态更加受到关注[1]。

在航天器相对运动的众多相关问题研究中，访问特定的空间相对位置对于很多航天任务均有重要的应用价值。当追踪航天器的轨道周期与目标航天器的轨道周期不同时，其相对运动轨迹在空间中是一条非闭合曲线，经过特定相对位置的轨迹可以用于确定空间非合作目标的运动状态[2]，近距离太空碎片清除[3]等任务。当轨道周期一致时，两航天器满足伴飞条件，可以实现长期的特定点重访任务，经过特定相对位置的轨迹对于航天器在轨服务[4]、空间攻防对抗[5]等任务有着重要意义。对于要求经过多个给定目标位置的轨道设计或确定问题，虽然在考虑惯性系下的航天器绝对运动轨迹时，有如给定两目标点与飞行时间的Lambert方法[6]、给定三共面目标点的Gibbs三矢量定轨方法[7]等经典方法，但是对于相对运动下的此类问题，由于坐标系是旋转坐标系，所以给定的空间相对位置在惯性系下不是固定不变的，并不能够通过绝对轨道的相关理论得到访问特定相对位置的相对运动轨迹，因此，对于相对运动空间中的三矢量定轨方法的研究，在航天器在轨服务、空间攻防对抗等任务中，对目标航天器从特定方位(特定相对距离及特定方向)上进行侦查等任务中具有重要意义。

另一方面，由于空间相对距离往往较近，相对速度较小，所以相对运动的动力学及运动学模型在对问题的研究中比惯性空间的绝对轨道动力学模型更具优势。在航天器相对运动问题研究中，线性相对运动模型因其可以得到解析形式的状态转移矩阵而得到广泛研究与应用。针对目标航天器为圆轨道和椭圆轨道，基于相对位置和速度的经典Clohessy-Wilyshire(CW)方程[8]和Tschauner-Hempel(TH)方程[9]分别被提出和完善改进。同时，基于相对轨道根数的相对运动模型也以其更便于表示航天器间的轨道关系得到了充分发展[10]。线性化的相对运动模型相比于非线性动力学模型，虽然在精度上会产生些许误差，但解析解的存在为进一步研究复杂的相对运动问题提供了有利的条件,例如近距离交会对接任务[11]、航天器编队飞行任务[12]等。

线性模型的状态转移矩阵[13]可以提供经过两个空间相对位置的相对轨道设计算法。但是当给定三个相对位置或加以伴飞约束条件时，问题的求解复杂度也会随之提升。对于访问空间中多个相对目标点的伴飞轨道设计问题求解，目前仍少有相关的理论方法，Bai等[14]首次通过相对轨道根数模型将问题转化为求解七维非线性方程组的问题，并对其进行了细致的后续维持策略研究，为此类问题的研究提供了新的思路。但其对于非伴飞情况没有进行考虑。同时，方程组的维度过高，会提升迭代过程收敛的难度。而以相对轨道根数模型对问题进行分析，对于航天器相对位置速度状态的体现也不足够直观。

基于以上有关介绍，本文以相对位置速度的直观状态量入手，将惯性空间中的三矢量定轨方法拓展到相对运动空间中。基于CW与TH方程，对包括圆轨道、椭圆轨道以及共面、异面在内的情况进行综合分析，给出各种情况下的约束方程与自变量的个数，并且将各种情况下的特定相对位置访问问题均简化为一维或二维非线性方程组问题，同时给出简洁的迭代初值选取策略;提出一种比较简洁有效的空间特定相对位置访问方法。

1 坐标系介绍与问题描述

1.1 坐标系及坐标转换

本文共应用到两种参考坐标系，分别为地心惯性坐标系(ECI)及目标轨道坐标系(TOC)。ECI坐标系选为国际常用的J2000坐标系；目标轨道坐标系原点位于目标航天器质心，Z轴指向地球质心，X轴在轨道平面内垂直于Z轴且指向轨道速度方向，Y轴构成右手直角坐标系(指向轨道角动量的反方向)，如图1所示。

由ECI向TOC转换的坐标转换矩阵可以表示为以下形式：

(1)

式中：s*=sin(*),c*=cos(*);i,Ω分别为S0的轨道倾角和升交点赤经；u=ω+f为纬度幅角，ω,f分别为近地点幅角和真近点角。

需要注意的是，由于TOC系是一个旋转坐标系，在进行速度转换时，需要对其进行考虑。位置和速度的转换关系式应分别写为：

(2)

1.2 相对运动的状态转移矩阵

在相对运动的问题研究中，针对主星圆形轨道的CW方程以及椭圆主星轨道的TH方程都是线性化的常用方程。二者都可以写成状态转移矩阵的形式，避免了数值积分，为相对运动相关问题的研究提供了十分便捷的基础条件。本文的后续分析求解等工作也均基于CW或TH方程进行，此处对二者的状态转移矩阵形式做简要介绍。

首先，相对运动状态转移矩阵的一般化形式可以写为：

(3)

对于式(3)中的各分项Φ，当S0轨道的偏心率e0≠0时，即为TH方程的状态转移矩阵，其表达形式在文献[13]及[15]中有着详细的描述与介绍。而当e0=0时，则可化简为CW方程的状态转移矩阵，表达形式如下：

(4)

1.3 问题描述与分析

访问给定相对位置条件下的轨道确定问题可以描述为：求解跟随航天器S1的轨道参数，使其能够在t1,t2和t3时刻分别经过给定的两个或三个相对目标位置R1,R2和R3。特别地，周期性重访约束条件是指S1的轨道周期与S0的轨道周期一致，使其能够周期性经过给定的相对目标位置。

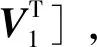
同时，约束方程的数量从问题描述中即可确定。假设S1在t1时刻以R1的相对位置出发，其需要满足的约束方程为

(5)

因此，约束方程的数量在异面条件时为6，共面条件时则为4。

通过上述分析可以发现，本文的研究问题可以分为以下四种情况：

(1)e0=0,S0与S1轨道共面：约束方程数量为4，待求解参数数量为4；

(2)e0=0,S0与S1轨道异面：约束方程数量为6，待求解参数数量为5；

(3)e0≠0,S0与S1轨道共面：约束方程数量为4，待求解参数数量为5；

(4)e0≠0,S0与S1轨道异面：约束方程数量为6，待求解参数数量为6。

所以，对于情况(1)和(4)，其约束方程数量与待求解参数数量相同，可以直接对问题进行分析求解研究；对于情况(2)和(3)，待求解参数的数量分别少于、多于约束方程的数量，使得相应问题不存在一般解或具有无穷多解，则可以通过调整改变约束条件使其约束与变量个数一致。本文中，重点考虑的额外约束条件为周期性重访约束。对情况(2)，减少一个目标相对位置，同时增加周期性重访约束；对情况(3)，额外增加周期性重访约束，则二者的约束方程数量与待求解参数数量均为5，可进行相应分析求解。

结合以上分析，本文将对以下四种情况分别进行访问给定相对位置条件下的轨道确定问题求解：

(a)e0=0,S0与S1轨道共面，过三个目标相对位置；

(b)e0=0,S0与S1轨道异面，过两个目标相对位置，周期性重访；

(c)e0≠0,S0与S1轨道共面，过三个目标相对位置，周期性重访；

(d)e0≠0,S0与S1轨道异面，过三个目标相对位置。

2 问题求解

2.1 情况(a)：共面圆轨道过三目标

当e0=0,S0与S1共面时，由式(3)和(4)可以写出访问三个给定目标相对位置的4个约束方程：

(6)

通过对方程组中的①②④式进行消元处理，省略中间过程，可以得到Δt3关于Δt2的解析表达式：

(7)

式中：

其中：

将式(7)代入式(6)中的③式，即可得到只关于时间Δt2的一元一维非线性方程，记为

F(Δt2)=0

(8)

其中涉及到的V1z和V1x表达式为：

(9)

(10)

可以通过分段黄金分割+割线法等常用的一维数值搜索算法快速求其在自变量约束范围内的所有可行解。

需要说明的是，由于本文研究中使用的是线性相对运动模型，得到的结果在真实的飞行环境下由于空间中的各种摄动力的作用，会存在位置误差(短时间内误差量级较小，具体情况将在第3节仿真算例中给出)。但这种误差都可以通过后续的微分修正过程进行修正，本文的方法仍然可以用于快速设计标称轨道。

2.2 情况(b)：异面圆轨道周期重访二目标

当目标相对位置包含面外量时，根据1.3节的分析，首先将目标位置数量减少至2个，同时增加周期性重访约束，此时问题的约束方程可以写为：

(11)

不难发现，当只需经过R1和R2时，由式(11)中的上式可以直接将相对速度V1写成关于时间Δt2的函数形式：

(12)

也就是说，任意的飞行时间Δt2都可以确定S1在相对位置R1处的相对速度V1，因此，只需要求解Δt2使得其对应的V1能够满足a1=a0即可。所以，需要建立起S1轨道的半长轴a1关于其在相对位置R1处的相对速度V1的函数关系。

由式(2)可以得到在t1时刻，S1在ECI系下的位置和速度矢量为

(13)

同时，由活力公式可知

(14)

结合式(13)及(14)，即可得到a1关于其V1的函数关系：

(15)

G(Δt2)=a1-a0=0

(16)

同样可以通过一维数值搜索算法在给定的时间约束范围内求解。

2.3 情况(c)：共面椭圆轨道周期重访三目标

当S0的轨道为椭圆轨道时，状态转移矩阵需采用TH方程的形式[15]。根据2.3节情况(c)可以建立问题的约束方程组为式(17)～(19)。

(17)

(18)

a1=a0

(19)

式(17)和(18)中的Φ,R,V均只考虑XZ平面内分量。同时V1可以表示为下面两种形式

(20)

对方程组作消去V1处理，可以将约束方程组重新写为式(21)及(19)的形式。

V1,t1t2-V1,t1t3=0

(21)

此时方程组维度为3，待求解参数为t1,t2及t3。对于维度大于1的非线性方程组，通常采用Newton迭代的方法对其进行求解，但是需要给出合理的迭代初值以保证收敛性。如果采用离散化网格点搜索算法，理论上，方程组的维度每增加一维，初值搜索的计算量都将巨量增加。所以，如何快速提供迭代初值是解决此问题的关键。

注意到虽然约束条件有所不同，但是S1轨道的半长轴a1的表达形式是一致的，均可以由式(15)表示。与情况(b)不同的是，由于e0≠0,a1不再只是关于Δt2的一元函数，而是关于t1和t2(或t3)的二元函数，而这取决于V1的表示方式选择为式(20)中的上式或下式。分别记两种a1的表示方法为如下形式

(22)

则当t1给定任意值时，对应满足周期性重访约束的t2和t3可以分别通过H1及H2以一维数值搜索方法确定。这一结果可以直接降低方程组的迭代维度。基于该结果，方程组可降维并重新写为：

(23)

对式(23)进行一维数值搜索求解，即可得到该情况下问题的解。

2.4 情况(d)：异面椭圆轨道过三目标

对于情况(d)，也是最具有一般性的情况，其约束方程可以表示为如式(17)和(18)的形式。

此时，Φ,R,V既包含面内量，也包含面外量。同样对方程组进行消元运算，消去V1，方程组即可重新写为如式(21)一样的形式。

不同的是，此时这是一个三维的非线性方程组，同样很难直接搜索得到迭代求解的初值点。所以，仍然需要通过一定的方法对方程组进行降维简化处理。注意到在相对运动的方程中，XZ平面内的运动与Y轴上面外的运动是互相解耦的。也就是说，此时该问题的方程组可以分别写为二维的XZ面内运动方程组和一维的面外运动方程。面内的二维方程组的形式与情况(c)完全相同，此处主要对面外的一维运动方程进行分析。Y轴方向轨道面外的运动方程记为

(24)

式中：根据文献[15]有

(25)

将式(25)代入式(24)，整理后可得：

(1+ecf2)sf3-f1R2y-(1+ecf3)sf2-f1R3y-(1+

ecf1)sf3-f2R1y=0

(26)

由轨道方程可知

(27)

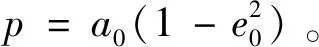
(28)

不难看出，在式(28)中，f1～f3,r1～r3都分别为t1～t3的函数，同时，r2又可以写作f2的显式函数。所以，将式中与f2相关的项提取出来，整合后可得：

Pcf2+Qsf2+E=0

(29)

式中：

(30)

通过三角函数关系求解方程，可得

(31)

式中：

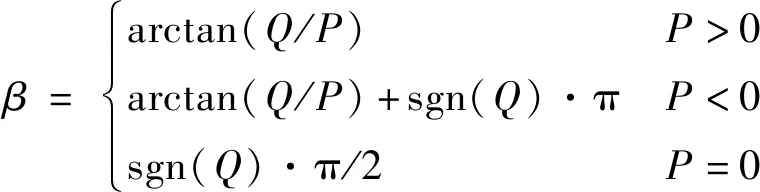
(32)

求解得到f2以后，时刻t2则可以通过求解Kepler方程获得。

在中国，椰子的种植面积相对于其他作物还是较少的，更多的人考虑到研究成果的市场问题之后都选择了放弃。所以，对于这种地域性较强的科研项目，国家要加大政策和资金扶持力度，发挥政府在组织创新方面的鼓励、支持、引导和协调的重要作用，为合作组织带动型的发展创造良好的外部环境，这也能为中国海南建设国际旅游岛提供动力 。

通过上述过程，我们将方程组中的面外方程转化为了一个t2关于t1和t3的表达式。这样，方程组可以被简化为只包含t1,t3的二元二维方程组。这对于迭代求解的初值选取工作是十分有利的。对于二元二维的非线性方程组，其迭代初值可以通过网格法[16]轻松获取。设计指标函数如下式：

U(t1,t3)=‖V1,t1t2-V1,t1t3‖

(33)

式(33)中的Φ,R,V均只考虑XZ平面内的分量。

利用网格法将t1和t3进行网格化，计算U的值，进行网格法搜索。选择U值较小的网格点作为初值，进行Newton迭代求解方程组，即可得到区间内的解集。

2.5 J2摄动模型下的解

2.5.1微分修正法

通过前文的理论过程，已经可以得到二体引力模型下该系列问题的解，但考虑到实际太空飞行环境中还包含有各种摄动力的影响，且以地球非球形引力摄动的J2项影响尤为明显。二体引力模型的假设以及基于线性相对运动模型得到的解在真实物理环境下会有相应的位置访问误差，因此，为了提高方法的实用性，还需要对J2摄动模型下的相应问题进行求解。本文采用微分修正法[16]求解此问题。

微分修正的基本步骤可以描述如下：

步骤1：确定待修正参数向量x，以及误差向量Er；

步骤2：通过数值差分算法，求取误差向量Er关于待修正量x的Jacobian矩阵J；

步骤3：通过如下迭代公式，对x进行修正，直至误差大小满足给定的指标。

xm+1=xm-J-1Er,m=1,2,…

(34)

式中：m为迭代次数。当m=1时，x1作为迭代初值，即为二体模型下的解。

2.5.2修正参数的确定

具体的，对于前文分析的四种情况，进行微分修正时，自由变量x及误差向量Er分别如下：

情况(a)：

(35)

式中：δR2x,δR2z,δR3x,δR3z分别表示在t2,t3时刻对R2,R3的面内X，Z方向上的位置访问误差。此时x与Er均为四维。情况(a)中对于t1的选择是任意的，考虑J2摄动时，仍然可以任意给定t1，因为在共面、不需要周期重访的条件下，J2摄动对轨道的影响程度较小。

情况(b)：

(36)

情况(c)：

(37)

情况(d):

(38)

式中：δR2,δR3分别表示t2,t3时刻，S1对目标相对位置R2和R3的三轴访问误差。此时x与Er均为六维。对于不含有周期重访约束条件的情况，可以直接对三轴访问位置误差进行修正。

通过以上过程，分别将二体模型下得到的结果作为初值在J2摄动模型下进行迭代修正，就可以得到相应的J2摄动模型下的解。下面给出各种情况的仿真算例。

3 仿真算例

在仿真中，首先需要给出各种情况下的S0的轨道参数，以及对应情况下S1所需要访问的特定目标点的相对位置。相关参数见表1。

S0轨道的其他参数在各情况下均为

[a0,i0,Ω0,ω0,ft0]=[12000 km,30°,60°,45°,0°]

(39)

下面分别对四种情况给出算例。

3.1 情况(a)：共面圆轨道过三目标

由2.1节的理论分析过程可知，在该情况下，Δt3可以表示为Δt2的显式函数，问题转化为一元一维非线性方程。但需要注意的是在求解反三角函数时，在[0,2π]区间内存在两个解，要注意分别考虑。

给定时间约束范围为Δt2∈(0,2T],Δt3∈(0,2T]。T为S0的轨道周期。在给定的时间约束范围内，通过分段黄金分割+割线法对方程在时间区间内进行一维数值求解，得到该问题的解集。同时，由于圆轨道条件下t1时刻不会对相对运动情况产生影响，因此对于情况(a)和情况(b)，均选取t1为初始时刻，即t1=0。

表1 S0轨道偏心率、需访问目标点及周期性重访约束初始条件Table 1 Orbital eccentricity of S0,positions to be visited and periodic revisit constraints

此外，将S1在访问R2和R3时所飞行的“圈数”分别为N2和N3，记为：

(40)

最终可以得到问题的解集，进一步以二体线性模型下的解为初值进行微分修正，可以得到与二体线性模型解逐一对应的J2摄动模型下的解，解集可见表2中的情况(a)。

用数值积分的方式，分别绘制二体模型下的解和修正得到的非线性J2摄动模型下的解在非线性J2摄动力学模型下的相对运动轨迹图，结果如图2所示。图中Pi(i=1,2,3)表示矢量Ri(i=1,2,3)在空间中的位置。可以看出在非线性J2摄动力学模型下，基于二体线性模型得到的结果也可以保证较高的访问精度，经计算，其对于R2,R3的访问误差分别为[0.049,5.968] m。而当经过修正后，对应的J2下的1号解则可以实现更为精确的访问，即使修正过程没有对Y轴的面外方向进行考虑，访问误差也均可被降低至10-2m量级。

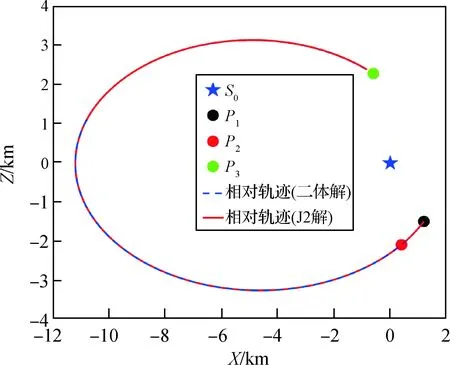
图2 情况(a)相对运动轨迹Fig.2 Relative motion trajectories of Case (a)

3.2 情况(b)：异面圆轨道周期重访二目标

由2.2节的分析可知，情况(b)的相关约束最终可化简为式(16)的关于Δt2的一元一维非线性方程。考虑到周期重访的约束条件，只需在Δt2∈(0,T]的时间约束范围内，通过分段黄金分割+割线法即可快速求解即可。将得到的解进行微分修正，得到J2摄动模型下的解，结果记录如表2中的情况(b)所示。

表2 J2摄动条件下各情况解集Table 2 Solutions of each case under J2 perturbation condition

将二者分别在J2摄动模型下积分得到的相对运动轨迹图如图3所示，考虑到周期重访约束，飞行轨迹的时间区间设置为[t1,t1+5T]。

经计算，二体线性模型的解在5个轨道周期中，对R1,R2的访问误差分别从[0,0.069] m逐渐扩大至[220.436,228.684] m。而经过修正后的J2模型的解，相应的访问误差则从第一周期的精确访问缓慢扩大至第五周期的[109.531,100.327] m。可以看出J2模型下的解可以有效地降低周期访问误差。此外，还可以看出在该组仿真算例的条件下，二体线性模型得到的解与J2模型下的解较为接近，因此该组二体线性模型的解对R1,R2的周期访问误差较小，但仍可看出经过修正后的结果周期访问效果明显更佳。

3.3 情况(c)：共面椭圆轨道周期重访三目标

在该情况下，考虑周期性重访约束，t2和t3可以分别表示为t1的函数[式(22)]。从而通过t1可以直接求得J(t1)的值。考虑有周期性重访约束，给定时间约束范围为t1∈[0,T],t2∈(t1,t1+T],t3∈(t1,t1+T]。

在t1∈[0,T]的范围内，在时间范围约束内，求解J(t1)=0，得到可行解集，并通过微分修正，得到J2摄动模型下的解集如表2情况(c)所示。

绘制二体解与J2解在[t1,t1+5T]时间区间内，在非线性J2摄动力学模型下积分得到的相对运动轨迹如图4所示。可以看出二体线性模型下的解在J2摄动模型下，相对运动轨迹会随着时间产生漂移，从而导致位置访问误差逐渐增大，在5个轨道周期内，对R1,R2,R3的访问误差分别从[0,0.302,322] m快速扩大至[2391,2439,2026] m。但经过修正得到的J2模型下的解相较之下则可以保证更高的访问精度。经计算，修正后的解在5个周期内的相应位置访问误差分别从[0,0.172,3.005] m缓慢扩大至[114.280,131.392,36.193] m。可以看出经过修正后的解，能够有效地降低周期访问位置误差，保证一定的周期重访精度，对于近距离侦查观测等任务具有相应的应用价值。

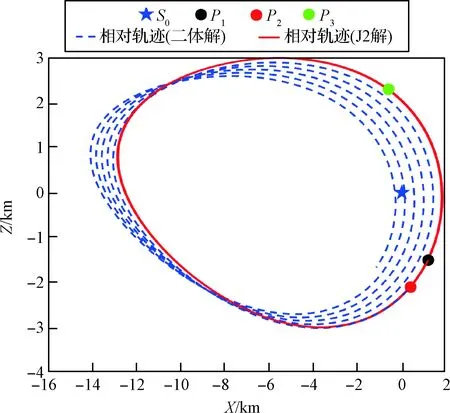
图4 情况(c)1号解相对运动轨迹Fig.4 Relative motiontrajectories of Case (c),solution No.1

3.4 情况(d)：异面椭圆轨道过三目标

由2.4节的分析可知，t2可以通过面外方程表示为t1,t3的显式函数，从而使三维非线性方程组降至二维，通过网格法搜索t1,t3的迭代初值。同样地，由于求解t2时需要进行反三角函数的运算，在搜索初值时也应对反余弦函数的符号正负分别考虑。由于情况(d)中不包含周期性重访约束条件，所以我们将飞行时间约束放宽至2T，即t1∈[0,T],t2∈(t1,t1+2T],t3∈(t1,t1+2T]。通过设定U的取值上界，筛选出较为合理的初值点。

为了更好地表示解的存在空间，以t1∈[0,T],t2∈(t1,t1+T]的时间区间，且式(32)的反三角函数取正号为例，以U<0.3 m/s为筛选条件，给出初值搜索的等高线图如图5所示，其他相应区间的搜索方法和结果均相同。

图5 初值搜索等高线图Fig.5 Contour map for searching initial values

将筛选出的初值点进行Newton迭代求解。借助于网格法搜索结果，从解的分布情况上着手，最终在时间约束范围内的可能存在解的区间内，求得相应的可行解，并通过修正过程，得到J2摄动模型下的可行解集合如表2情况(d)所示。

绘制二者在J2摄动模型下的相对运动轨迹如图6所示。可以看出在较短时间内，二体线性模型的解可以保持较高的访问精度。经计算，二体线性模型的解对R2,R3的位置访问误差分别为[93.464,29.065] m。而经过修正后，由于对三轴方向均进行了修正，因而可以实现精确位置访问。

图6 情况(d)1号解相对运动轨迹Fig.6 Relative motion trajectories of Case (d),solution No.1

4 结 论

对于访问多个特定相对位置的航天器轨道确定问题，按照目标航天器的轨道形状为圆或椭圆，以及目标航天器和追随航天器的轨道是否共面分为四种情况进行求解。其中，轨道异面，且目标航天器为圆轨道情况时，可以经过两个特定相对位置，并实现周期性重访。对于其他三种情况，均可以实现相对运动模型下的三矢量定轨。并且，共面且目标航天器为椭圆轨道的情况还可以实现周期性重访的三矢量定轨。通过理论分析推导，使每种情况下的问题最终都简化为求解一或二维非线性方程(组)的问题，并提出了有效的求解策略。并进一步基于二体线性模型得到的结果，通过微分修正策略，对不同的情况分别在J2摄动的力学模型中进行修正，并得到相应的J2摄动条件下的结果。

经过仿真分析，可以发现该问题的解并不唯一，存在多解现象。同时，本来采用线性相对运动方程得到的解，在飞行时间较短的情况下，在J2摄动模型中仍然具有较高的访问精度，但是当考虑周期重访条件，或飞行时间较长时，J2引力摄动对于访问精度会产生较大的影响。而通过微分修正方法，可以有效地降低其影响，提高访问精度。本文提出的方法可以有效地用于访问多个特定空间相对位置的航天器轨道设计。