丁三波,刘亚拴

(河北工业大学 人工智能与数据科学学院，天津 300401)

近年来,随着网络技术的迅速发展,网络化控制系统由于成本较低,便于维护,可以有效地实现远程控制和远程诊断,受到了学者的广泛关注。周期采样是一种常见的网络化控制方法[1-2]。此方法根据给定的采样周期,对系统输出进行周期性采样和传输。周期采样利于系统的设计与分析,但可能会产生冗余采样信号,造成通信带宽的浪费。为避免此类问题,学者引入了事件触发控制(Event-triggered control,ETC)。在事件触发控制中,只有在某一变量超过给定阈值时,控制器执行更新任务,有效地节约了通信带宽资源[3-5]。目前,事件触发控制已经广泛存在于各个领域的研究[6-8]。

离散时间系统是很常见的物理系统,针对离散时间系统的事件触发控制也屡见不鲜。如Shen等[9]研究了一类具有随机参数和不完全测量的离散时间混合时滞神经网络的事件触发状态估计问题。Hu等[10]研究了一类离散时间随机系统的事件触发机制控制问题,探讨了数据丢包问题。文献[9-10]设计的事件触发方案均采用了传统的误差测量方式,以状态反馈为例,传统测量误差的定义为常采样信号与系统当前状态之间的差。在触发时刻kl到下一次触发时刻kl+1内,被控对象在控制信号的作用下,系统状态的演化整体趋势是收敛的,所以测量误差会随时间逐步增大,而这会导致测量误差很容易超过预设的常数阈值或时变阈值,使得相邻触发间隔较小,造成较高的触发频率。

本文从状态预测或逼近的角度,针对离散线性/非线性系统分别逐段构造了状态逼近解,逼近解可以跟随闭环系统离散状态的局部变化趋势,实现减少测量误差的目的。设计了基于状态逼近解的事件触发控制器,并得到了闭环系统的稳定性判据。同时,本文将该方法结合动态事件触发策略[11],通过增大触发阈值,达到更好的控制效果。最后通过数值仿真验证了该方法的有效性,并与传统事件触发控制器[15-16]作比较,表明状态逼近法可以有效地降低采样次数,减少通讯带宽的浪费。

1 线性系统的事件触发控制

考虑如下离散线性系统:

x(k+1)=(A+ΔA)x(k)+Bu(k)

(1)

式中：x(k)=col[x1(k),x2(k),…,xn(k)]∈Rn为状态变量,u(k)∈Rq为要设计的控制器,A∈Rn×n和B∈Rn×q为常数矩阵。ΔA∈Rn×n为参数扰动。假设ΔA=EΣ(k)F,其中ΣT(k)Σ(k)≤I,E∈Rn×p,F∈Rp×n为已知矩阵。

在传统的事件触发控制[15-16]中,往往将控制器u(k)设计为

u(k)=Kx(kl)

(2)

式中kl≤k≤kl+1-1,K∈Rq×n为控制增益矩阵。通过定义ef(k)=x(k)-x(kl),设计如下触发条件：

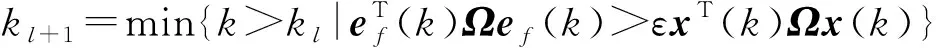
(3)

式中：Ω∈Rn×n为一个正定的常数矩阵,ε>0为触发阈值。

事件触发策略(3)实际上是将常采样信号x(kl)代替了控制器u(k)=Kx(k)中的系统状态x(k),或者说是常采样信号x(kl)用来逼近系统当前状态x(k),这容易造成较高的触发频率。基于上述方法的局限性,本文提出基于状态逼近的事件触发控制方法。

对于无参数扰动系统：

x(k+1)=Ax(k)+Bu(k)

(4)

式中控制器为u(k)=Kx(k),系统(4)在k∈[kl,kl+1-1]上的解析解为x(k)=(A+BK)k-klx(kl),不妨将该解析解视为系统(1)的状态的逼近解来研究系统(1)的稳定性。

令xg(k)=(A+BK)k-klx(kl),构造控制器为

u(k)=Kxg(k)

(5)

式中k∈[kl,kl+1-1]。定义测量误差eg(k)=x(k)-xg(k),设计事件触发条件为：

k0=0

(6)

式中：Ω∈Rn×n为正定常数矩阵,ε>0为触发阈值。

联立系统(1)和控制器(5),可以得出：

Δx(k)=(A+ΔA+BK-I)x(k)-BKeg(k)

(7)

式中Δx(k)=x(k+1)-x(k)。

在定理1中,给出了系统(1)基于控制器(5)和事件触发条件(6)的控制下渐近稳定的充分条件。

定理1对于给定的触发阈值ε>0和控制增益矩阵K∈Rm×n。如果存在恰当维数的矩阵P>0,Ω>0,N=col[N1,N2,N3],以及正常数r0使下列条件成立,则事件触发条件(6)和控制器(5)可以保证闭环系统(1)是渐近稳定的。

(8)

其中：

r0FTF+εΩ

证明考虑下面Lyapunov函数：

V(k)=xT(k)Px(k)

(9)

计算V(k)的差分,可得

ΔV(k)=V(k+1)-V(k)=

xT(k+1)Px(k+1)-xT(k)Px(k)=

ΔxT(k)Px(k)+2xT(k)Px(k)

(10)

令ξg(k)=col{x(k),Δx(k),eg(k)},则对于适当维数的矩阵N=col[N1,N2,N3],以及正常数r0,下列不等式条件成立：

EΣ(k)F)x(k)-BKeg(k)]≤

BKeg(k)]+r0xT(k)FTFx(k)+

(11)

对于k∈[kl,kl+1-1],由事件触发条件(6),有

(12)

联立式(10)～(12)可得

(13)

其中

(14)

根据Schur补定理,条件(8)等价于Π<0。证明完成。

文献[12]提出了离散时间系统的动态事件触发方案。这种方法实际上是增大了触发的阈值。本文的方法完全可以结合动态事件触发方案进行推广,进而降低网络的通讯负担。定义如下γ(k)变量:

εxT(k)Ωx(k)

(15)

式中γ(0)≥0,相应的动态触发条件为：

k0=0

εxT(k)Ωx(k))<0}

(16)

式中0<ρ<1,θ≥1/ρ。文献[12]证明了在区间k∈[0,+∞)中,γ(k)≥0,所以动态触发条件(16)可能会比静态触发条件(6)产生较少的触发次数。

注2触发条件(16)在增加了触发阈值的同时,减小了测量误差的取值。从降低系统通讯负担的角度而言,将是一种更好的选择。当θ趋于无穷时,触发条件(6)可以看作式(16)的极限情况。

推论1对于给定的触发阈值ε>0和控制增益矩阵K∈m×n。如果定理1中的条件成立,则在事件触发条件(16)和控制器(5)可以保证闭环系统(1)是渐近稳定的。

ΔxT(k)PΔx(k)+2ΔxT(k)Px(k)+

εxT(k)Ωx(k)≤

ΔxT(k)PΔx(k)+2ΔxT(k)Px(k)-

(17)

将式(17)代替定理1中的式(10)和式(12),其余证明与定理1相似,在这里不再赘述。

2 非线性系统的事件触发控制

考虑如下离散非线性系统：

x(k+1)=(A+ΔA)x(k)+

(W+ΔW)f(W0x(k))+Bu(k)

(18)

式中x(k)=col[x1(k),x2(k),…,xn(k)]∈n为状态变量,u(k)=Kx(k)为要设计的控制器,W∈Rn×m和W0∈Rm×n为系统矩阵。ΔA∈Rn×n,ΔW∈Rn×m为参数扰动。且满足ΔA=EΣ(k)F,ΔW=GΘ(k)H,其中ΣT(k)Σ(k)≤I,ΘT(k)Θ(k)≤I。E、G、F、H为已知矩阵。非线性函数f(·)=col[f1(·),f2(·),…,fm(·)]。其余符号与系统(1)一致。

假设函数fr(·)满足fr(0)=0以及下面条件：

(19)

式中l1r、l2r为已知常数。记l1=diag{l11,l12,…,l1m},l2=diag{l21,l22,…,l2m}。

注3本文假设非线性系统(18)满足Lipschitz条件(19)。在实际中,有许多系统满足该条件[17-20],例如经典的Hopfield神经网络模型、Lur’e型系统、蔡氏电路系统以及Ikeda-type振荡器等。

对任意满足条件l1≤L≤l2的常对角矩阵L,将离散非线性系统(18)线性化近似为带有参数扰动的线性系统:

x(k+1)=[A+ΔA+(W+ΔW)LW0]x(k)+Bu(k)

(20)

对于无扰动离散系统：

x(k+1)=(A+WLW0)x(k)+Bu(k)

(21)

式中控制器为u(k)=Kx(k)。可以得到系统(21)在k∈[kl,kl+1-1]的解析解为

xh(k)=(A+BK+WLW0)k-klx(kl)

(22)

将解析解(22)当作系统(18)的逼近解。构造如下控制器：

u(k)=Kxh(k)

(23)

式中k∈[kl,kl+1-1]。定义eh(k)=x(k)-xh(k)。设计如下事件触发条件：

k0=0

(24)

式中：Ω∈Rn×n为正定常数矩阵,ε>0为触发阈值。

联立系统(18)和控制器(23),可得

Δx(k)=(A+ΔA+BK-I)x(k)+

(W+ΔW)f(W0x(k))-BKeh(k)

(25)

式中Δx(k)=x(k+1)-x(k)。

定理2给出了离散非线性系统(18)基于控制器(23)与事件触发条件(24)的稳定性判据。

定理2对于给定的触发阈值ε>0和控制增益矩阵K∈Rm×n。如果存在恰当维数的矩阵P>0,Ω>0,N=col[N1,N2,N3,N4],m阶对角正定矩阵Λ,以及正常数r1,r2,使下列条件成立,则事件触发条件(24)和控制器(23)可以保证闭环系统(17)是渐近稳定的。

(26)

其中：

证明考虑下面Lyapunov函数：

V(k)=xT(k)Px(k)

(27)

计算V(k)的差分,可得

ΔV(k)=V(k+1)-V(k)=

xT(k+1)Px(k+1)-xT(k)Px(k)=

ΔxT(k)PΔx(k)+2xT(k)Px(k)

(28)

令ξh(k)=col{x(k),Δx(k),f(W0x(k)),eg(k)},则对于适当维数的矩阵N=col[N1,N2,N3,N4],以及正常数r1,r2下列不等式条件成立：

EΣ(k)F)×x(k)+(W+GΘ(k)H)f(W0x(k))-

(A+BK-I)x(k)+Wf(W0x(k))-BKeh(k)]+

r1xT(k)FTFx(k)+r2fT(W0x(k))HTHf(W0x(k))

(29)

考虑关于非线性函数f(·),根据式(19),对于任何正定矩阵Λ∈m×m,下列不等式成立:

0≤2(f(W0x(k))-l2W0x(k))TΛ×
(l1W0x(k)-f(W0x(k)))

(30)

对于k∈[kl,kl+1-1],根据事件触发条件(24),有

(31)

联立式(28)～(31)可得

(32)

式中

(33)

根据Schur补定理,条件(26)等价于Ξ<0。证明完成。

定理2的结果可以结合动态事件触发策略进一步提高。定义如下μ(k)变量：

εxT(k)Ωx(k)

(34)

式中μ(0)≥0,由文献[12]可知,在区间k∈[0,+∞)中,μ(k)≥0。相应动态触发条件为：

k0=0

εxT(k)Ωx(k))<0}

(35)

式中0<ρ<1,θ≥1/ρ。

推论2对于给定的触发阈值ε>0,θ>0和控制增益矩阵K∈Rm×n。如果定理2中的条件成立,则事件触发条件(35)和控制器(23)可以保证系统(18)是渐近稳定的。

注4通过构造逼近解,本文将测量误差e(k)=x(k)-x(kl)改为eg(k)和eh(k),减小了测量误差的取值,有利于降低事件触发的次数。但是与传统事件触发方法相比[15-16],本文所提方法并不会降低稳定性判据的保守性。

3 数值仿真

例1在本例中,考虑倒立摆模型,其线性化动力学模型如下:

(36)

式中θ为摆角,u(t)为作用在小车上的力,摆锤质量m=0.1 kg,小车质量M=0.1 kg,摆锤长度l=0.136 m,这里取重力加速度g=9.8 m/s2,用ΔA=EΣ(t)F用以描述倒立摆控制系统的参数不确定性[21],取E=col[0.4 0.8],F=[0 0.1],Σ(t)=sin(t)。

令采样周期为0.005 s,通过将上式离散化得到:

(37)

考虑具有以下参数的离散线性系统,取K=[2.854 8 0.475 8],触发阈值ε=0.1。

通过LMI工具箱解线性矩阵不等式(8),可得

(38)

选取初始条件为x(0)=col[0.2,0],迭代次数取T=500。

图1、2分别为本文所提出的方法与传统事件触发方法[15-16]的控制器响应。本文所提出的方法触发次数为5次,传统事件触发方法的触发次数为69次。很容易看出本文所提出的方法策略能有效减少触发次数。

图1 控制器响应：状态逼近ETC方法

图2 控制器响应：传统ETC[15-16]

接下来,比较本文中基于状态逼近的动态触发控制与文献[12]的仿真结果,令式(15)中的ρ=0.5,θ=3,迭代次数为T=500。图3、4为控制器响

图3 控制器响应和动态变量γ(k)：状态逼近动态ETC

图4 控制器响应和动态变量γ(k)：文献[12]的动态ETC

应和动态变量γ(k)的仿真结果。仿真中,本文中基于动态触发条件(6)产生的事件触发次数为4次,而文献[12]中的方法为28次,是本文方法的7倍。因此,本文提出的状态逼近法可以有效减少事件发生的次数。

通过LMI工具箱解出线性矩阵不等式(26),可得

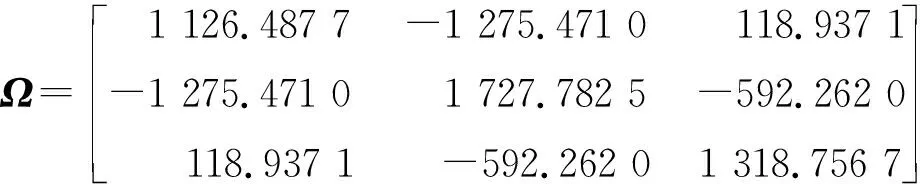
(39)

选择初始条件x(0)=col[3,-3,4],迭代次数T=50。图5、6分别给出了本文所提出方法与传统事件触发方法[15-16]对应的事件触发间隔。本文所提出的方法与传统事件触发方法的采样数量分别为6、22,可以看出本文所提出的方法策略能有效减少采样数量。

图5 事件触发时刻和间隔：状态逼近ETC方法

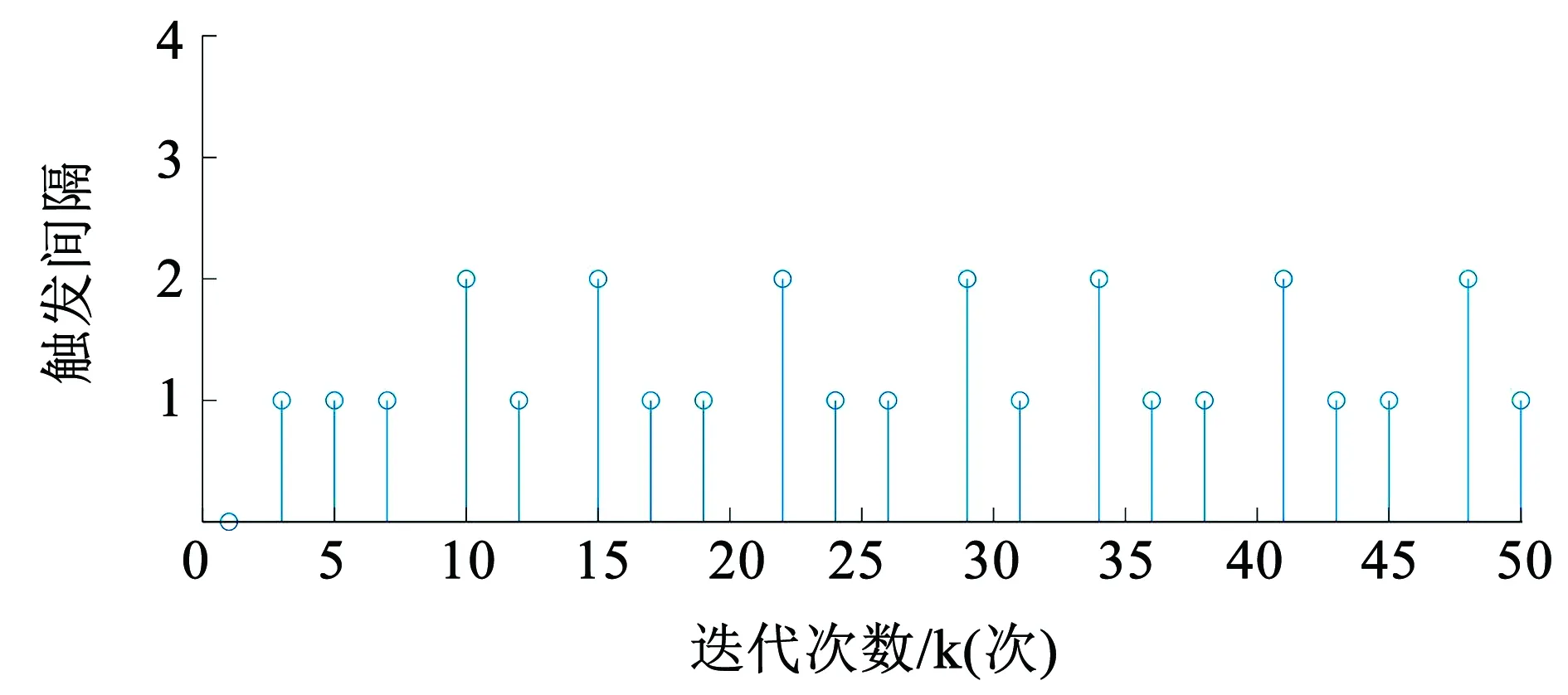
图6 事件触发时刻和间隔：传统ETC[15-16]

将文献[12]所用方法与本文中基于状态逼近的动态触发作比较,设动态触发条件(34)中的ρ=0.5,θ=3,迭代次数为T=50。图7、8分别给出了动态变量μ(k)和事件触发间隔的仿真结果。在图7中,本文方法基于动态触发条件(35)产生的事件数为4次,而在图8中,文献[12]中的方法为14次。本文提出的状态逼近法可以有效减少事件发生的次数,并且本文方法结合动态事件触发策略进一步减少了事件触发次数。

图7 动态变量μ(k)与事件触发时刻和间隔：状态逼近动态ETC

图8 动态变量μ(k)与事件触发时刻和间隔：文献[12]的动态ETC

4 结 论

1)针对带有参数扰动的线性/非线性系统,利用系统矩阵、采样信号和无扰动离散线性系统解析解的定义逐段构造状态逼近解,逼近解可以一定程度上跟随系统当前状态,减少测量误差。设计了基于状态逼近解的控制器和事件触发条件。通过构造Lyapunov泛函分别给出了线性/非线性系统稳定的充分条件。并将状态逼近法结合动态事件触发策略做了进一步研究。

2)通过列举倒立摆系统和蔡氏电路的实验表明,相比传统事件触发控制方法,本文提出基于状态逼近的事件触发控制方法产生的事件次数更少,可以有效地节约通讯带宽资源。