李雪，于志永，蒋海军，陈思宇

(新疆大学数学与系统科学学院，新疆乌鲁木齐 830017)

0 引言

在过去的十几年里, 受自然界中动物群体行为的启发, 人们对多智能体系统的群体行为展开了广泛的研究.随着嵌入式计算和通信能力的提高, 以及分布式思想的提出, 多智能体系统的分布式协同控制引起了众多学者的研究兴趣. 多智能体系统的分布式协同控制广泛的应用于传感器网络[1−2], 机器人编队控制[3−5]等.

多智能体系统的一致性是分布式协同控制中最基本的问题之一.所谓一致性是指一组多智能体通过局部信息交流达到某些状态相同的行为, 例如位置、速度、姿态等. 在一致性研究中, 系统的收敛时间是评价一致性协议的一个重要指标. 文献[6] 研究了有向间歇通讯下二阶多智能体系统的渐近一致性. 基于已有的渐近收敛结果, 在文献[7-8] 中提出了有限时间收敛的一致性协议. 文献[7] 研究了具有通信时间延迟和参数不确定性的多智能体系统有限时间主从一致性. 在文献[8] 中, 作者提出了一种鲁棒非脆弱状态反馈的设计方法, 研究了具有随机不确定性和非线性的多智能体系统有限时间一致性. 然而, 上述工作得到的停息时间的估计依赖于系统的初始状态和控制参数,这限制了控制协议的应用范围.为了使停息时间的估计不依赖系统的初始状态,研究者提出了固定时间一致性. 文献[9]研究了具有时滞和未知干扰的多智能体系统固定时间二部一致性. 进一步, 为了使系统在任意预给的时间内实现一致, 文献[10-11] 研究了多智能体系统的指定时间一致性.

在文献[10-11] 中, 作者考虑的都是理想环境下的多智能体系统一致性. 在实际应用中, 系统往往处于更加复杂的环境并且会遇到各种外部干扰. 因此, 具有外部干扰的多智能体系统一致性是一个值得关注的问题. 由于滑模控制具有对参数变化的不敏感性以及对干扰的完全抑制性等优点,滑模控制被用来处理系统的外部干扰问题. 利用滑模控制方法, 文献[12] 研究了有向拓扑上二阶非线性多智能体系统的有限时间一致性. 文献[13]分别在固定和切换拓扑下研究了具有时变时滞和干扰的高阶多智能体系统的一致性追踪问题.利用终端滑模控制理论, 文献[14] 研究了具有未知干扰的二阶多智能体系统的固定时间一致性问题. 在文献[15] 中, 作者提出了新的滑模控制协议并研究了非线性随机多智能体系统的一致性追踪问题. 文献[12-15] 都运用滑模控制理论研究多智能体系统的有限时间或固定时间的一致性问题, 但多智能体系统的指定时间一致性问题还未考虑. 与有限时间和固定时间一致性相比, 指定时间一致性的收敛时间可以是预先给定的任意值, 与系统初值和控制参数的设计无关. 因此, 运用滑模控制理论研究多智能体系统的指定时间一致性问题具有很大的挑战性.

本文旨在提出一种新的控制方法分别研究一般无向和有向网络上多智能体系统的指定时间一致性问题.与已有的工作相比, 本文的贡献主要包括以下三点: (1) 与文献[10-11]相比,本文考虑了具有外部干扰的多智能体系统,该系统能够应用于更加复杂的通讯环境.(2)基于积分滑模控制方法,本文提出了一种新型的控制协议.该协议克服了停息时间依赖系统初值的缺点并可以保证系统在指定时间内到达滑模面并实现一致. (3) 本文将无向网络拓扑下的结果推广到一般有向网络上, 推广了所提出的控制协议的应用范围.

1 预备知识与模型描述

为了方便, 我们先给出一些记号. Rn代表n 维欧氏空间. IN是N 维单位矩阵. 对于矩阵B, BT, λmin(B)和 λmax(B) 分别代表 B 的转置, 最小特征值和最大特征值. 对于向量 q, ‖q‖1, ‖q‖, ‖q‖∞分别代表 q 的 1 范数,2 范数和无穷范数. sign(q)=[sign(q1),···,sign(qN)]T, signα(q)=[|q1|αsign(q1),···,|qN|αsign(qN)]T, 其中α >0是一个常数, sign(·) 代表符号函数. 此外, ⊗代表矩阵的Kronecker 乘积, diag(·) 代表对角矩阵.

1.1 图论知识

三元组 G=(V,E,A) 表示由N 个节点组成的图, 其中V={v1,···,vN} 表示节点集, E 表示边集, A 表示加权邻接矩阵. 如果在 vi和 vj之间存在边, 则 (i,j)∈E. 在加权邻接矩阵 A=[aij]∈RN×N中, 如果 (j,i)∈E, 则有aij>0, 否则aij=0. 节点i 的邻居集表示为Ni={j ∈V:(j,i)∈E}. 如果在每个节点对之间存在一条有向边,则图 G 称为有向强 连通的. 图 G 的 Laplacian 矩阵 L=[lij]N×N定义为 L=D−A, 其中 D=diag(d1,···,dN) 称为度矩阵, 且d=Na. 对于主从多智能体系统, 智能体之间的通讯拓扑用图G 来表示, 且跟随者之间的通ij=1ij讯拓扑表示为图G¯. 领导者与第i 个代理之间的通信权重强度用bi表示. 如果第i 个代理可以接收领导者的信息, 则 bi>0, 否则 bi=0. 定义 B=diag(b1,···,bN).

1.2 指定时间稳定

考虑系统

其中: x(t)∈Rn是状态向量, f(·):Rn→Rn为非线性向量值函数, 且满足f(0)=0.

下面我们给出一些相关的定义和假设. 首先引入一个时变函数

其中: h>1 是任意实数, t1=t0+T, T >0 是一个指定的常数. 显然, 在 t ∈[t0,t1), µ−q(q>0) 是单调递减函数,且 µ(t0)−q=1, limt→t−1µ(t)−q=0. 此外，

定义 1[14]如果系统(1) 的平衡点是全局一致渐近稳定的, 并且存在一个函数T(t0,x0)≥0 使得系统的解x(t,t0,x0) 满足 limt→T(t0,x0)‖x(t,t0,x0)‖=0 且对于所有的 t ≥T(t0,x0) 有 x(t,t0,x0)=0, 则称系统 (1) 的平衡点是全局一致有限时间稳定的, 其中函数T(t0,x0) 被称为停息时间.

定义2[10]如果系统(1) 的平衡点是全局一致有限时间稳定的, 且停息时间的估计T >0 是任意给定的与初值无关的任意常数, 则称系统(1) 的平衡点是全局指定时间稳定的.

引理 1[10]对于系统(1), 如果存在一个非负连续可微函数V(x(t)): Rn→R 满足

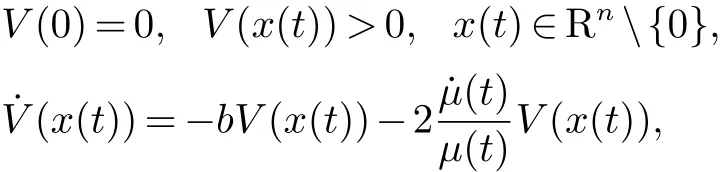
其中: b>0 是一个正常数, 则系统(1) 的平衡点是全局指定时间稳定的. 此外, 对于t ∈[t0,t1) 有

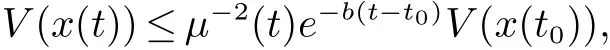
并且对于 t ∈[t1,∞) 有

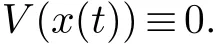
1.3 模型描述

考虑具有一阶非线性动力学的领导跟随多智能体系统, 其动力学描述为

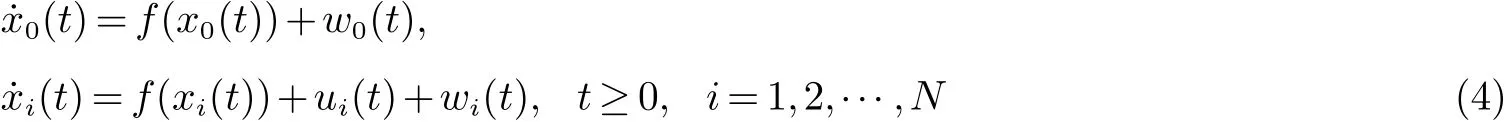
其中: x0(t) ∈Rn, w0(t) ∈Rn分别表示领导者的状态和外部干扰, f(x0(t)) 表示领导者固有的非线性动力学.xi(t)∈Rn, ui(t)∈Rn, wi(t)∈Rn分别表示第i 个跟随者的状态、控制输入和外部干扰. f(xi(t)) 表示第i 个跟随者固有的非线性动力学.在实际系统中外部干扰一般都是未知的,为得到更精确的收敛结果,我们假设外部干扰是可以被测量的, 即存在 F >0, D>0 使得 ‖w0(t)‖∞≤F <∞, ‖wi(t)‖∞≤D<∞.

定义3 对于多智能体系统(4) 的任意初值以及任意给定的正数T >0, 如果

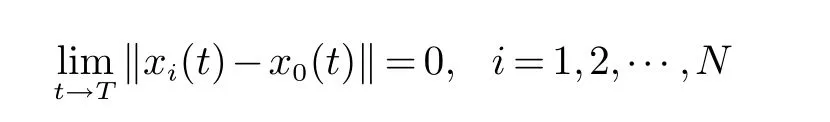
成立, 则称多智能体系统(4) 在指定时间内达到一致.

假设 1 对于非线性函数f(·), 存在非负常数ρ1使得

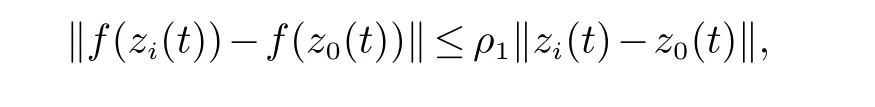
其中: zi(t),z0(t)∈Rn.

假设 2 网络通讯拓扑G 包含至少以一个领导者为根节点的有向生成树, 并且跟随者之间的网络通讯拓扑¯G 是无向的.

假设 3 网络通讯拓扑G 包含至少以一个领导者为根节点的有向生成树, 并且跟随者之间的网络通讯拓扑¯G 是有向的.

2 主要结论

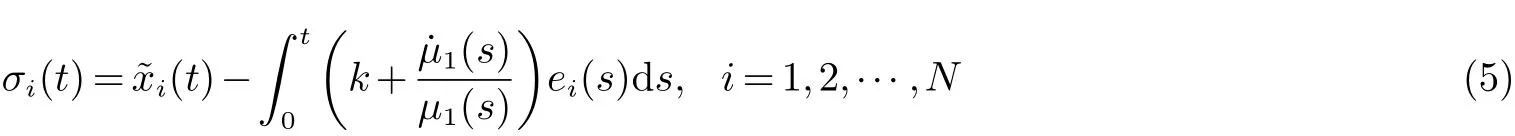
其中: k>0, µ˙1(t) 为(3) 中定义的形式且指定时间为T1=t1+T. 根据滑模控制理论, 当系统误差进入滑模面时能体系统(4) 在指定时间内达到领导跟随一致, 第i 个跟随者的控制器设计如下

在学生工作中，要做到因事而化、因时而进、因势而新。辅导员的工作要贴近学生，不能脱离学生的实际，针对学生的现状及时调整工作的方式方法，在不断调整与改进中迎难而上、锐意改革、积极创新，以改革创新的方法来解决发展中的问题，不断增强学生思政工作的时代感和吸引力。

其中: k,k1,k2>0 是待定的设计参数.

定理 1 考虑多智能体系统(4), 若假设1 和假设2 成立, 且控制器(6) 中的参数k,k1,k2满足下列条件

则多智能体系统(4) 在控制器(6) 下指定时间内达到一致.

证明 对于t ∈[0,t1), 我们考虑如下Lyapunov 函数

将Vi(t) 沿着(5) 式求导可得

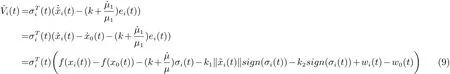
根据假设1 可得

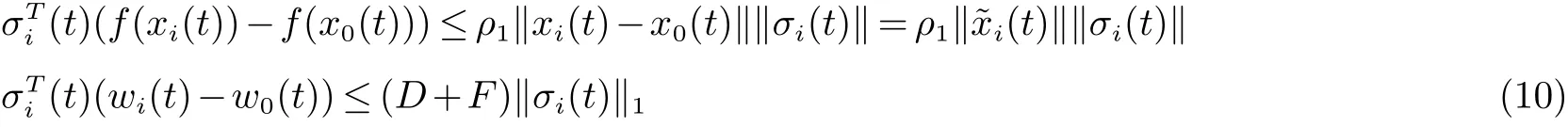
根据引理1 可得

当 t →t−1时，µ−2→0, 我们就有 ‖σi(t)‖→0. 因此, 多智能体系统 (4) 可以在指定时间 t1内到达滑模面.

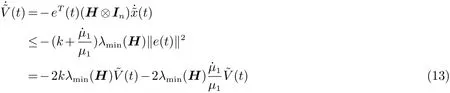
基于引理1 可知, 当t=T1时可得˜V(T1)=0. 因此, e(T1)=0. 根据假设2 中网络拓扑图G 包含至少以一个领导者为根节点的有向生成树, 可知矩阵H 是可逆的. 所以limt→T1˜x(t)=0. 由上述证明我们就可以得到在指定时间T1内系统达到一致.

下面我们将上述结果推广到一般有向网络拓扑上.

定理 2 考虑多智能体系统(4), 若假设1 和假设3 成立, 且控制器(6) 中的参数k,k1,k2满足下列条件

则多智能体系统(4) 在控制器(6) 下指定时间内达到一致.

证明 对于t ∈[t0,t1),类似于定理1 的分析,我们可以得到多智能体系统(4)在指定时间t1内到达滑模面.

对于 t ∈[t1,∞), 我们记 L+B = H. 由假设 3 可知, 矩阵 H 是不对称的, 则存在矩阵 P > 0 使得P H+HTP =Q>0. 设ˆV(t)=eT(t)(P ⊗In)e(t), 对ˆV(t) 求导可得

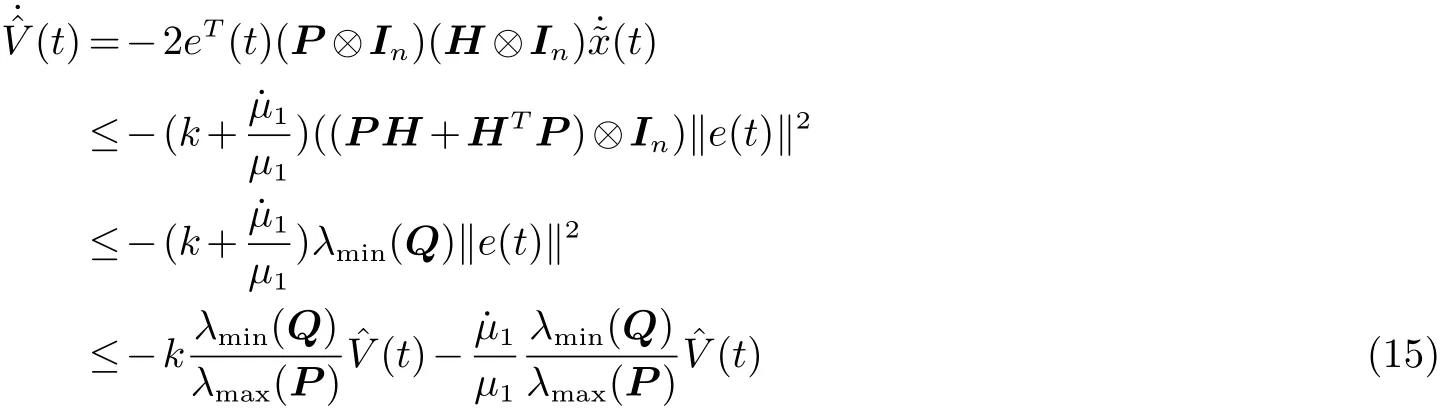
基于引理1 可知, 当t=T1时可得ˆV(T1)=0. 因此, e(T1)=0. 因为矩阵Q, P 是可逆的, 所以limt→T1˜x(t)=0.由上述证明我们就可以得到在指定时间T1内系统达到一致.

注 1 定理1 考虑的是一般无向网络拓扑上多智能体系统的指定时间一致性问题. 与定理1 相比, 定理2考虑的是一般有向网络拓扑, 由于矩阵H 是不对称的, 需要选择正定矩阵P 使其对称化.

3 数值仿真

为了说明控制协议的有效性, 我们给出如下的数值算例.

例 1 考虑具有一个领导者和四个跟随者的多智能体系统(4), 领导者与跟随者之间的无向拓扑如图1(a)所示. 非线性函数定义为

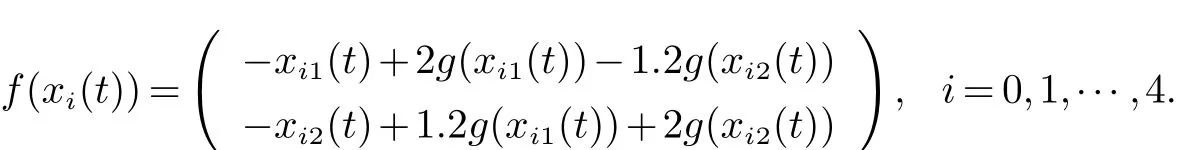
其中: g(xij(t))=0.5(|xij(t)+1|−|xij(t)−1|)+0.01sign(xij(t)),i=0,1,···,4,j=1,2. 系统的外部干扰为 w01(t)=w02(t) = 0.05sin(t)+0.1cos(t), w11(t) = w12(t) = 0.05sin(t)+0.1cos(t), w21(t) = w22(t) = 0.05sin(t)+0.1cos(t),w31(t)=w32(t)=0.05sin(t), w41(t)=w42(t)=0.1cos(t) 并且满足‖w0(t)‖∞≤ 0.2, ‖wi(t)‖∞≤ 0.2,i=1,2,3,4. 通过简单计算, 我们选取控制参数为k=0.01, k1=6.8, k2=8.5, h=1.5, 由此定理1 的条件都成立. 数值模拟结果如图2∼5 所示, 图2 和图4 描述的是无控制下系统的状态与滑模变量的状态, 图3 和图5 分别描述的是在控制协议(6) 下, 智能体的状态以及滑模变量的状态. 显然多智能体系统可以在指定时间内到达滑模面并实现一致.

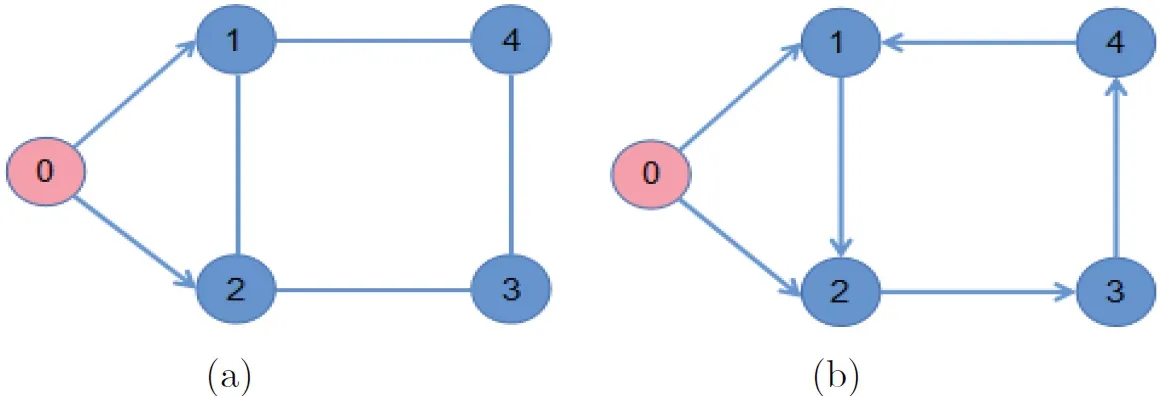
图 1 通讯拓扑图

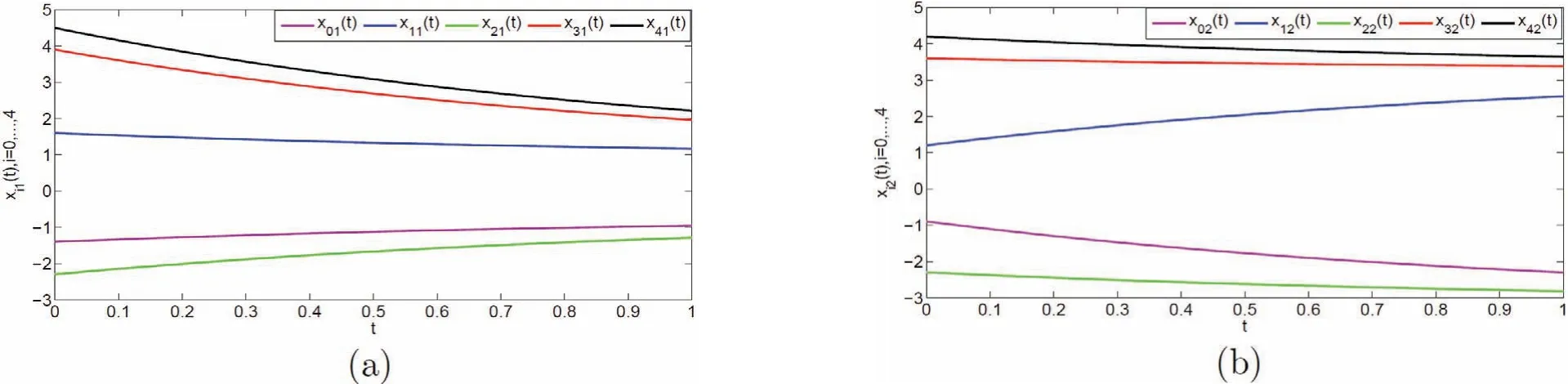
图 2 无控制下智能体的状态轨迹

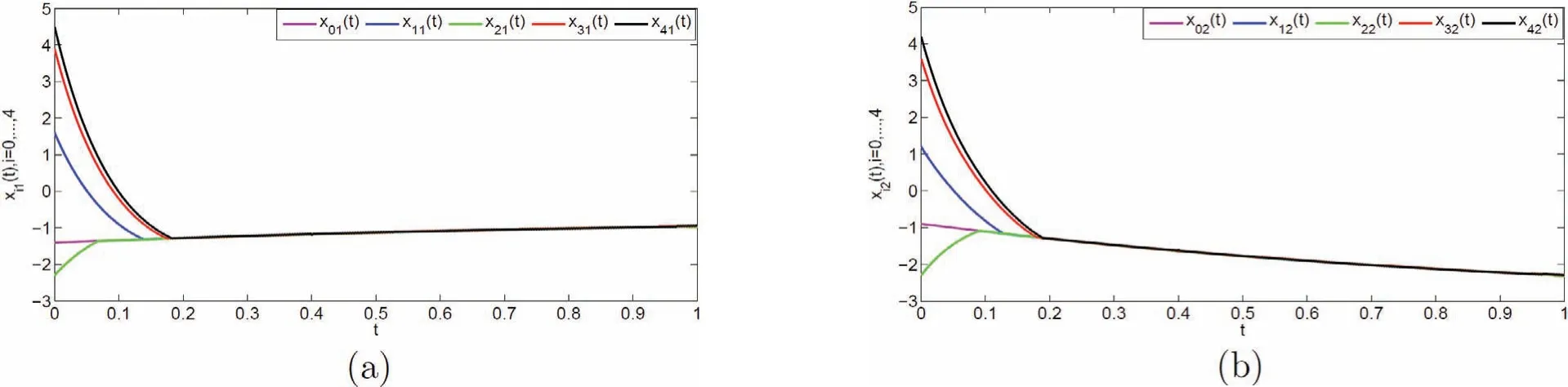
图 3 在控制协议(6) 下智能体的状态轨迹

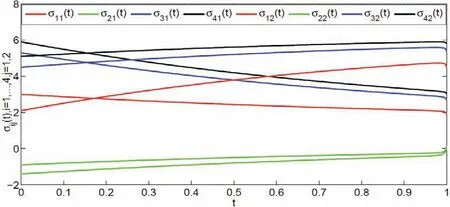
图 4 无控制下滑模变量的状态

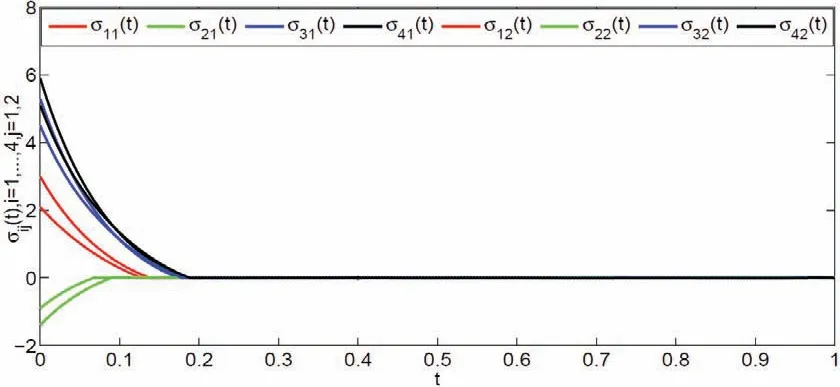
图 5 在控制协议(6) 下滑模变量的状态

例 2 考虑具有一个领导者和四个跟随者的多智能体系统(4), 领导者与跟随者之间的有向拓扑如图1(b)所示. 非线性函数f(xi,vi,t) 和系统外部干扰与例1 中的相同. 我们选取控制参数为k=0.01, k1=2.8, k2=3.5,h=1.7, 通过简单计算, 定理 2 的条件都成立. 数值模拟结果如图 6∼9 所示, 图6 和图 8 描述的是无控制下系统的状态与滑模变量的状态, 图7 和图9 分别描述的是在控制协议(6) 下, 智能体的状态以及滑模变量的状态.显然, 多智能体系统也可以在指定时间内到达滑模面并实现一致.

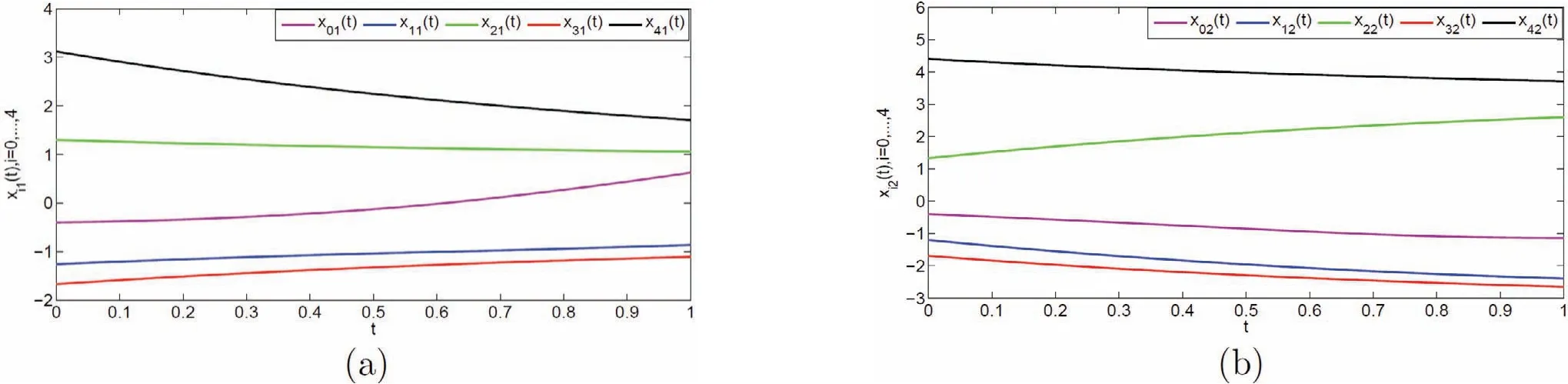
图 6 无控制下智能体的状态轨迹

图 7 在控制协议(6) 下智能体的状态轨迹

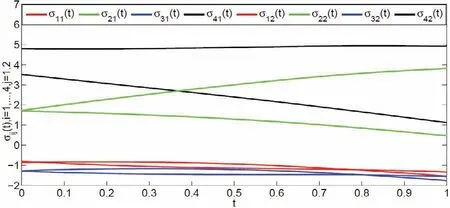
图 8 无控制下滑模变量的状态

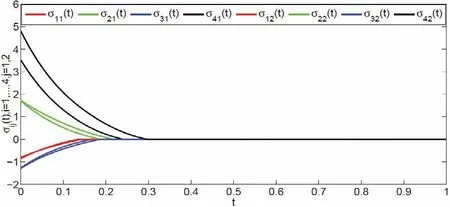
图 9 在控制协议(6) 下滑模变量的状态

4 结论

本文研究了无向和有向网络上的多智能体系统指定时间一致性问题. 基于滑模控制理论, 我们设计了新型的积分滑模面并提出了新的控制协议. 利用Lyapunov 稳定理论和不等式放缩技巧, 证明了多智能体系统可以在指定时间内达到滑模面并实现一致, 并给出两个数值算例来验证理论结果的有效性. 在未来的工作中, 我们将考虑高阶多智能体系统的指定时间一致性问题.