安徽省合肥市第四中学 郑 良（邮编：230601）

《普通高中数学课程标准（2017 年版2020 年修订）》中指出高中数学学科核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析. 立体几何是高中数学的重要组成部分，在培养与考查学生的直观想象、逻辑推理和数学抽象等核心素养中发挥着不可或缺的作用.其中直观想象素养包含空间想象能力、直观洞察能力及用图形语言来思考问题的能力，教学中应在直观想象的基础上培养学生的抽象思维能力，借助几何直观把复杂抽象的数学问题变得简明形象. 立体几何问题的解法包括传统几何法和空间向量法，空间向量法又可分为坐标法和基底法. 传统几何法解题主要考查空间想象能力，而难一点的题目，思维难度通常要求较高，辅助线学生难以作出，坐标法解题过程较程序化. 空间向量法的引入，将几何问题转化为代数问题，可以借助向量法的运算，程序化地“算出”几何的结果，减少了复杂的思维和推理过程，为空间感较弱的学生提供了“救命稻草”，因而备受师生们的青睐，建系已经成为解决立体几何问题的一种常用方法. 坐标法运用的前提是建系并标出点的坐标，但有时不易建系，或建系后不易直接求出相关点的坐标，有时也不清楚利用点的坐标求得的方程表示的几何意义等等. 因此，利用坐标法有时能降低难度，使学生更容易上手；有时可能会增加难度，让问题更加扑朔迷离. 下面以高三复习检测中部分立体几何试题为载体，给出简答，剖析学生困惑与“错误”，结合教学实践给出思考与建议.

1 试题分析

1.1 几何体的外接球问题

高中数学一般不会直接求球的方程，而是求球的相关度量，如球心到截面圆的距离、截面圆的半径或面积，球的表面积与体积等. 若求球的半径，主要有两种方式：（1）先确定球的球心再确定球的半径；（2）构造模型直接求出球的半径.

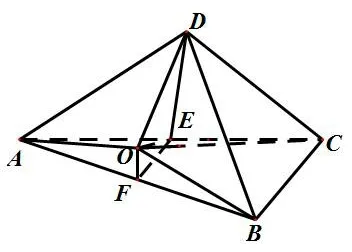
图1

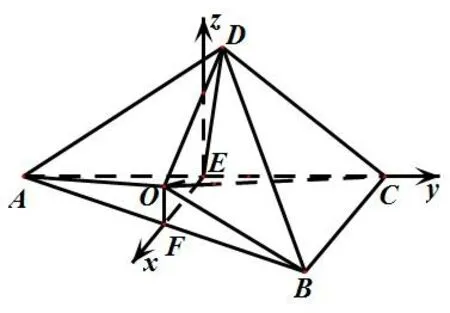
图2

评析本题可在直线l（到A,B,C距离相等的点的轨迹）上取点O利用OA=OD求解，不重不漏，但过程繁琐. 解法1 借助RtΔACB和RtΔACD确定四面体ABCD外接球的球心，重复使用A,C点，以退为进更快确定O的位置，本质为交集思想方法的灵活运用. 解法2 为坐标法，运算量大.

1.2 截面问题

在立体几何中，截面是指用一个平面去截一个几何体(包括圆柱，圆锥，球，棱柱，棱锥、长方体，正方体等等)得到的平面图形. 在立体几何中将一个“平面（图形）”放大的常用方式有两种：一是将其中一条或两条直线延伸，二是过平面的一点，作平面内某一条直线的平行线. 另外，作截面涉及到直线与平面的交点，这通常转化为直线与直线的交点，因此截面问题可综合考查直线与平面之间的位置关系.

例2 （合肥市2022 年高三第二次教学质量检测文科数学第12 题）在直三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=AA1=2，P为三棱柱表面上一动点，若CP=B1P，则P点的轨迹长度为（ ）

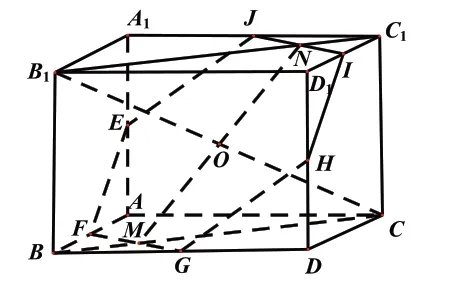
图3

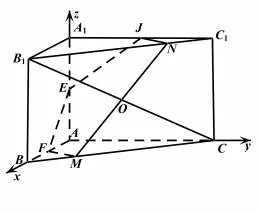
图4

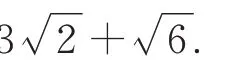
点评解法1 将三棱柱还原为正方体，利用正方体的截面确定该三棱柱的截面，事半功倍；解法2 为坐标法，确定平面EFGHIJ的方程后，还需利用公理（基本事实）才能确定线段MN. 对于特殊情况，综合法常常简捷，对于一般情况，往往坐标法更快捷，但有时挖掘代数形式方程的几何意义也不容易. 当题目给出的图形不能直接判断是什么样的几何体，往往是命题人通过截取几何体的一部分呈现出来，考查空间想象能力. 为了解题时抓住本质，使问题的解决有依托，可以把它补充完整，使它成为我们常见的几何体.

1.3 空间中点、直线、平面的位置关系

空间基本图形的位置关系问题是立体几何的核心内容，其中又以直线与直线、直线与平面、平面与平面的平行和垂直问题为重点.《普通高中数学课程标准（2017 年版2020 年修订）》明确要求“立体几何初步”的学习，可以以长方体为载体，帮助学生认识和理解空间点、直线、平面的位置关系. 表述平行、垂直的性质与判定时，大多也是从长方体开始的. 立体几何中的基本图形有长方体、直三棱柱、正三棱锥、球、圆锥等. 弄清基本图形的性质与相互关系是前提，然后对基本图形进行改造，深化对问题的认识与理解.

例3 （合肥市2022 年高三第二次教学质量检测理科数学第16 题）在正方体ABCD-A1B1C1D1中，E为线段AD的中点，设平面A1BC1与平面CC1E的交线为l，则直线l与BE所成角的余弦值为______.

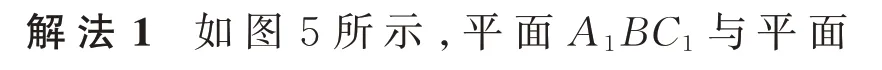
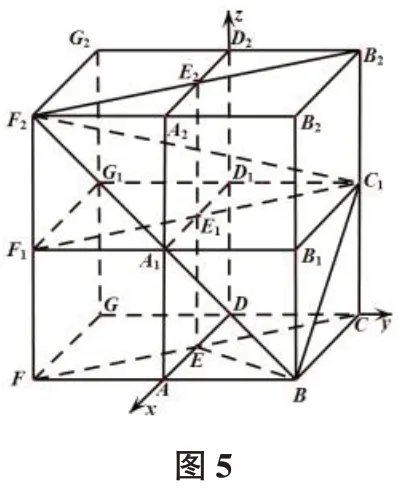
图5

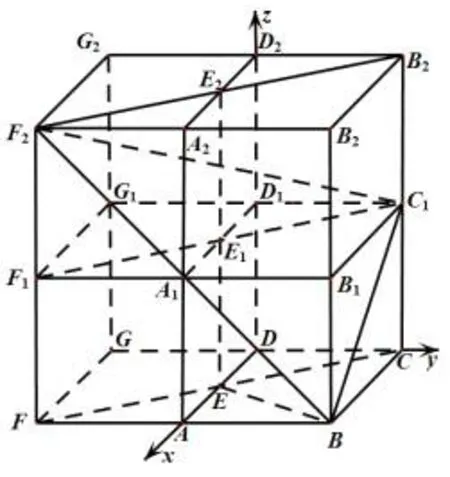
图5

点评解法1 用公理确定直线l，解法2 用平面向量基本定理确定直线l. 由于本题求解两条异面直线所成的角，只与其方向有关而与具体位置无关，解法3 从平面的法向量角度确定直线l的方向向量.

1.4 图形的折叠问题

把一个平面图形按某种要求折起，转化为空间图形，进而研究图形在位置关系与数量上的变化，这就是翻折问题. 立体几何折叠问题从知识和方法层面可以有效地考查空间点、直线、平面之间的位置关系，以及空间角、空间距离、空间体积、面积等，从能力和素养层面可以有效地考查对空间图形的观察与分析、对比与想象等数学能力，有助于发展直观想象、逻辑推理和数学运算等核心素养. 翻折过程使得平面图形变成空间立体图形，我们需要抓住一个关键点，就是同一平面内的元素信息不发生变化.

例4 如图6，在直角梯形MBCD中，MB //CD，BC⊥CD，MB=2BC=2CD=2，A是MB的中点，将△MAD沿AD折起，使得点M到达点P处，且平面PAD⊥平面ABCD，连接PB，PC，如图7，E是线段PB的中点.F,G,H分别在线段AE,PC,AC上运动，则FG+GH的最小值为（ ）

图6

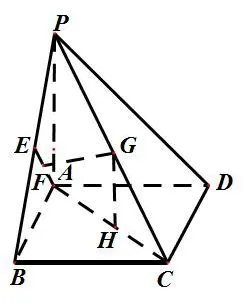
图7

解法1 由题意可知，平面PAB⊥平面PBC，过点G作GF1⊥PB，则GF1⊥平面PAB；过点G作GH1⊥AC，则GH1⊥平面ABCD. 如图8 所示，则FG+GH≥GF1+GH1≥H1F1=1. 当且仅当F与E重合，G,H分别为线段PC，AC的中点时等号成立.

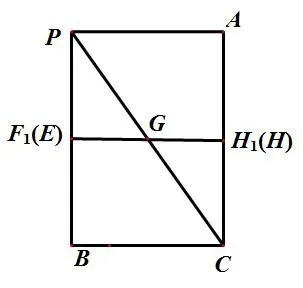
图8

评析解法1 为综合法，本题中AE⊥平面PBC，连接EG，则一定有AE⊥GE，此时确定F即为点E，对于任意一点G，当且仅当GH⊥AC时，GH最小，转化为点G到点E和线段AC的距离之和最小问题. 解法2 为坐标法，由于λ,γ均与μ有关，故先固定μ，利用非负性逐步放缩. 部分学生采用解法2，无法求出函数的最值.

2 思考与建议

2.1 重视理解数学概念 明晰定理功能作用

数学概念乃是现实世界中空间形式和数量关系及其特有的属性（或本质属性）在人的思维中的反映. 每一个数学概念都有其确定的内容和含义. 为了正确地刻画每一概念的内容和含义，概念之中必然地存在几个关键词反映了这一概念的本质属性. 因此，在概念的教学中要注意强调概念中关键词的意义. 如异面直线、截面等的定义. 由于在解答或证明数学问题时，定理有时会起到极其重要的“桥梁”作用，有时也是作图和添加辅助线的重要依据. 因此，我们必须重视定理的教学. 要使学生透彻地理解定理、掌握定理、活用定理，我们必须做到：第一讲清定理的条件和结论. 第二讲清定理的证明方法. 第三讲清定理的作用及适用范围. 同时还要构建定理之间的联系，进而构建立体几何的逻辑与结构. 如例2中内切球的概念是确认内切球存在的唯一标准，例6 中两个平面垂直的判定定理与性质定理等.综合法往往通过作辅助线构建不同对象之间的联系，而定理为图形作辅助线指明方向.

2.2 强化挖掘问题背景 领悟思想优化方法

数学家华罗庚说过，复杂的问题要善于“退”，足够地“退”，“退”到最原始而不失去重要性的地方，是学好数学的一个诀窃. 教学时，我们不能停滞于问题答案的获得，还要揭示出问题的背景，从局部到整体；我们也要在整体中聚焦局部细微之处. 重视挖掘题目的来源，如课程标准中的案例、教材中的例题与习题、高考真题、竞赛题等，站在命题人的角度进行构造. 如例3 中，我们可从正方体的截面角度来认识，又如例1 中确定三棱锥外接球的球心位置的方法等.

3.3 问题解决（综合法、向量基底法、坐标法）三法并举 综合法优先夯实根基

多数立体几何试题都可以采用综合法、向量基底法、坐标法. 学生更喜欢用向量法，因为向量法几乎是程序化的操作，思维量比较少，导致学生不愿意花时间去审题，不想用综合法去分析问题.久而久之，立体几何对学生的应有培养功能得不到充分发挥. 从这些年的情况来看，学生的数学学科素养呈现下降趋势，这有违引入空间向量的初衷. 师生“淡化”综合方法，突出坐标法主要原因有两个层面：（1）师生心理层面. 立体几何是训练和考查学生空间想象能力最主要的载体，但在实际教学中发现，有相当一部分学生缺乏基本的空间观念，不能有效认识立体几何直观图，不能辨别图中点、直线、平面的位置关系，师生都期望通过空间向量坐标运算来弥补这个缺憾，从而在平时教学中过于强调用向量坐标法解题（有的甚至只用向量坐标法解题），导致习惯性用向量坐标法求解立体几何问题.（2）知识能力层面. 因为学生缺乏较高的空间想象能力和扎实的立体几何基础知识，不能有效地利用综合法解题. 向量的通性通法，无论在教学上还是解题上都具有导向作用. 从教学的角度来看，向量结构比度量结构更为简单.而且在向量空间中，要遵守的规定的数量比欧氏几何要少. 从这个角度来说，运用向量来解决问题还是具有无可比拟的优越性. 因此，在教学中要把握素养培养这个大方向，对立体几何教学综合法和向量法不能有所偏废，要让学生走出“向量万能”的误区，优先使用综合法解题的意识，重视综合法的讲解与训练，因题而异，灵活选择解题方法. 教师首先应该在平时讲题以身作则，给学生做好榜样；其次，在学习综合方法解决立体几何后不应急于向学生讲授向量法，这样不利于学生空间想象能力的提高；当然不可避免地会遇到运用综合法出现解题困难，这需要老师和学生尽可能多地研究对策. 另外，在用向量法解决问题后，应养成继续探求用传统方法解题（验证）的好习惯. 在教学中通过典型例题引导学生对比辨析，强化学生运用综合法解决立体几何问题的能力，让学生在观察、探索、发现、解决问题的过程中，提高学生的识图能力、作图能力、空间想象能力和逻辑推理能力，发展学生的直观想象素养.