CHARACTERIZATION OF RESIDUATED LATTICES VIA MULTIPLIERS*
2022-11-04WeiWANG王伟BinZHAO赵彬
Wei WANG (王伟) Bin ZHAO (赵彬)
School of Mathematics and Statistics,Shaanxi Normal University,Xi’an 710119,China
E-mail: wangwei135420@snnu.edu.cn;zhaobin@snnu.edu.cn
Abstract In the paper,we introduce some of multipliers on residuated lattices and investigate the relations among them.First,basing on the properties of multipliers,we show that the set of all multiplicative multipliers on a residuated lattice A forms a residuated lattice which is isomorphic to A.Second,we prove that the set of all total multipliers on A is a Boolean subalgebra of the residuated lattice (which is constituted by all multiplicative multipliers on A) and is isomorphic to the Boolean center of A.Moreover,by partial multipliers,we study the maximal residuated lattices of quotients for residuated lattices.Finally,we focus on principal implicative multipliers on residuated lattices and obtain that the set of principal implicative multipliers on A is isomorphic to the set of all multiplicative multipliers on A under the opposite (dual) order.
Key words residuated lattice;multiplier;M-multiplier;PI-multiplier;T-multiplier
1 Introduction
It is well known that various logical algebras have been proposed as the semantic systems of non-classical logical systems which are formal and useful tools for computer science in forms of dealing with uncertain and fuzzy information.Residuated lattices [32],as the semantics of Hhle’s Monoidal Logic,were introduced by Ward and Dilworth,and are very basic and important logical algebras.Many logical algebras are particular cases of residuated lattices,such as MV -algebras [6],BL-algebras [13],Heyting algebras [5] and MTL-algebras [9],etc.For the least two decades,the study of operator theories on these logical algebras can be divided into two classes.One consists of operators with a logical background,like modal operators[18],monadic [28] and internal states [14];some of those operators can be used to extend logical semantics.The other class consists of operators that stem from analytic theories or pure algebras;these can be used for characterizing the algebraic structure of logical algebras,such as closure operators [30],derivations [15],multipliers [3] and nuclei [12].In summary,various kinds of operators (special mappings) play a very helpful role when it comes to research on logical algebras.
The concept of multipliers [20,24] first appears in harmonic analysis in connection with the theory of summability for Fourier series,and it has been employed in other areas of mathematics and physics,such as Banach algebras [21,31,33] and locally compact groups,partial differential equations,spectral theory [34] andC*-algebras [1,2],lattice-order algebras and logical algebras[3,8,17,26,29],etc..In the theory of summability for Fourier series,the multipliers can be used to describe those sequences {bn} for whichis always the Fourier series of a periodic integrable function wheneveris such a Fourier series.From [2,21,31],a mappingTon a Banach algebraB(orC*-algebras) into itself is called a multiplier ifT(ab)=(T a)b=a(T b)for alla,b∈B.The multipliers can not only be used to study the representation theory for Banach algebras,but can also characterize order-bounded operators inC*-algebras and give a characterization of the relative commutant of sub-C*-algebras with a unit.Analogously,a multiplier on a semigroup (A,*) [20,29] is a functionffromAintoAsuch thatf(x) *y=x*f(y) for allx,y∈A.As is well known,every commutative idempotent semigroup is a semilattice,so the theory of multipliers be developed quickly on lattices.In [25],Noor gave an equivalent characterization by multipliers for each nearlattice that has a decomposition into a direct summand.[8] and [29] present many particularly fruitful results regarding multipliers on distributive latticesL,and show that the latticeM(L) of multipliers is the maximal extension ofLwhich containsLas a join-dense ideal,in particular,giving a nonstandard construction of the maximal lattices of quotients for a distributive lattice.Following this,multipliers were introduced to many prevalent logical algebras such as MV-algebras [26],BL-algebras [3] and MTL-algebras [27] for the same purpose.Although those logical algebras are still distributive lattices,the algebraic structures of them become relatively complex.Influenced by this fact,the notion of multipliers on such logical algebras has changed,and the definition has become complicated by fours axioms (see Definition 4 of [3] or Definition 3.11 below).Meanwhile,another kind of multiplier (we call it an implicative multiplier) is discussed inBE-algebras [19],d-algebras [7] andBL-algebras [17] etc.,in order to depict algebraic structure.In particular,in[17],Khorami and Saeid discussed the relations between such multipliers and other operators,like closure operators,homomorphisms and derivations,and studied theMV-center ofBLalgebras via implicative multipliers.
Based on the above,a natural question arises: what are the relations among such different kinds of multipliers on the same logical algebra? In this paper,we show that for every total multiplier on a residuated lattice,there exists a unique implicative multiplier such that two multipliers form a Galois connection (the more detailed information about the relation between these multipliers is shown in Figure 1 (in Section 4)).In addition,the paper is motivated by the following considerations: (1) ForMV-algebras andBL-algebras,etc.,we have observed that,although they are different algebras,they are all particular types of residuated lattice.Hence,it is meaningful to extend the concept of multipliers to the more general fuzzy structures for studying the common properties of such operators.(2) we try to clarify the connection between ideals and multipliers on residuated lattices and use multipliers to give the maximal residuated lattices of quotients for residuated lattices.(3) we want to characterize residuated lattices draw support from multipliers.
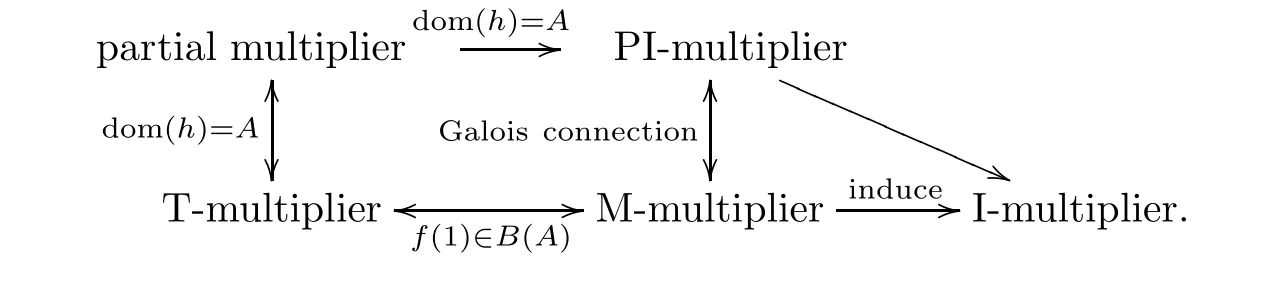
Figure 1 The relation of different types of multipliers on residuated lattice,where the notion “A B” means “A should be B” or “B can be induced by A”,and dom(h)denotes the domain of h.

Figure 2 Here φ,ψ and Bo are the mappings defined in Theorem 3.4,Theorem 4.6 and Theorem 3.15,respectively.“C D” means that “C should be isomorphic to D”,and“C D” means that “C is a special case of D or assign C to its Boolean center D”.
This paper is organized as follows: in Section 2,we review some basic definitions and results on residuated lattices.In Section 3,we introduce the notion of M-multipliers and partial multipliers on a residuated latticeAand study the relation of M-multipliers and partial multipliers.Moreover,by the properties of multipliers,the maximal residuated lattices of quotients of residuated lattices are studied.In Section 4,PI-multipliers on residuated lattices are presented,and the relations among M-multipliers,(partial) multipliers and PI-multipliers are investigated.
2 Preliminaries
In this section,we recall some fundamental concepts related to the theory of residuated lattices and of lattices in general which shall be needed in the sequel.
Definition 2.1(see [32]) An algebraic structure (A,∧,∨,⊙,→,0,1) of type (2,2,2,2,0,0)is called a residuated lattice provided that it satisfies the following conditions:
(1) (A,∧,∨,0,1) is a bounded lattice,
(2) (A,⊙,1) is a commutative monoid,
(3)x⊙y≤zif and only ifx≤y→z,for allx,y,z∈A,where ≤is the partial order of its underlying lattice (A,∧,∨,0,1).
Throughout this paper,byAwe denote the universe of a residuated lattice (A,∧,∨,⊙,→,0,1).For anyx,y∈A,definex*=x→0,x**=(x*)*andx⊕y=x*→y.B(A)={x∈A|x∨x*=1} is the set of all complemented elements of its underlying bounded lattice(A,∨,∧,0,1) and is the universe of a Boolean subalgebra ofA(called the Boolean center ofA).DefiningG(A)={x|x⊙x=x,x∈A},we haveB(A) ⊆G(A).
Definition 2.2(see [9,13,23]) LetAbe a residuated lattice.ThenAis called
(1) a divisible residuated lattice,ifx∧y=x⊙(x→y),∀x,y∈A;
(2) an MTL-algebra,if (x→y) ∨(y→x)=1,∀x,y∈A;
(3) a BL-algebra,ifx∧y=x⊙(x→y) and (x→y) ∨(y→x)=1,∀x,y∈A;
(4) an MV-algebra,if (x→y) →y=(y→x) →x),∀x,y∈A.
Proposition 2.3(see [9,13,16,32]) In any residuated latticeA,the following properties hold:
(1) 1 →x=x,x→1=1,0*=1,1*=0,
(2)x≤yif and only ifx→y=1,
(3)x≤yimpliesy→z≤x→z,z→x≤z→yandx⊙z≤y⊙z,
(4)x⊙y≤x∧y,y≤x→x⊙y,
(5)x→(y→z)=(x⊙y) →z=y→(x→z),
(6)x⊙(y∨z)=(x⊙y) ∨(x⊙z),x∨(y⊙z) ≥(x∨y) ⊙(x∨z),
(7) (x∨y) →z=(x→z) ∧(y→z),x→(y∧z)=(x→y) ∧(x→z),
(8) ifAis anMT L-algebra,thenx→(y∨z)=(x→y) ∨(x→z),
(9) ifAis a divisible residuated lattice,thenx⊙(y∧z)=(x⊙y) ∧(x⊙z),
(10) ifAis aBL-algebra,then (x∧y) →z=(x→z) ∨(y→z),for anyx,y,z∈A.
Proposition 2.4(see [4,10]) Letx,y∈Aande,f∈B(A).Then
(1)e⊙e=eande=e**,
(2)e→(x→y)=(e→x) →(e→y),
(3)e∨(x⊙y)=(e∨x) ⊙(e∨y),e∧(x⊙y)=(e∧x) ⊙(e∧y),
(4) e*→x=(e→x) →x=e∨x,
(5)e∧e*=0,
(6)e⊙x=e∧x,
(7) (e→x) ∨(e*→x)=1,
(8)e⊙(x→y)=e⊙(e⊙x→e⊙y),
(9)x⊙(e→f)=x⊙(x⊙e→x⊙f),
(10) (e∧x)=e⊙(e→x)=x⊙(x→e),
(11)e,f∈B(A) impliese→f∈B(A).IfAis anMV-algebra,then
(12)e∈B(A) iffe⊙e=eiffe⊕e=e,
(13)e∧(x⊕y)=(e∧x) ⊕(e∧y),e∨(x⊕y)=(e∨x) ⊕(e∨y).
Definition 2.5(see [11]) Let (X,≤) and (Y,≤) be two posets,f:X→Yandg:Y→Xbe two order-preserving maps.Then a pair (f,g) is called a Galois connection betweenXandYprovided that,for anyx∈X,y∈Y,f(x) ≤yiffx≤g(y).
From [22],a lattice ideal is a nonempty setI⊆Asatisfying that: for anyx,y∈A,(I1):x≤yandy∈Iimplyx∈I;(I2):x,y∈Iimpliesx∨y∈I.An ideal is a nonempty setI⊆Athat satisfies (I1) and (I3) (where (I3):x,y∈Iimpliesx⊕y∈I).
3 Multiplicative Multipliers and Partial Multipliers on Residuated Lattices
This section concentrates on discussing the multiplicative multipliers (simplify,M-multipliers)and partial multipliers on residuated lattices.We use partial multipliers to study the maximal residuated lattice of the quotient of a residuated lattice.
Definition 3.1A mappingf:AAon a residuated latticeAis said to be a multiplicative multiplier (simplify,M-multiplier) onAif it satisfies that ∀x,y∈A,f(x⊙y)=x⊙f(y).
Example 3.2(1)idA(i.e.,f(x)=xfor anyx∈A) is an M-multiplier on a residuated latticeA.
(2)0A(i.e.,f(x)=0 for anyx∈A) is an M-multiplier on a residuated latticeA.
(3) LetA={0,a,b,c,1},0<a <b <c <1,⊙and →be defined as follows:

Then (A,∧,∨,⊙,→,0,1) is a residuated lattice andfc(x)=c⊙xis a M-multiplier onA.
(4) The standardMV-algebra (a special residuated lattice) is anMV-algebra [0,1]MV=([0,1],⊕,*,0),wherex⊕y=min{x+y,1},x*=1 -x.The derived operations are as follows:x⊙y=max{x+y-1,0}x→y=min{1 -x+y,1},x∨y=max{x,y},x∧y=min{x,y}.Then the functionf(x)=max{x-0.5,0} is an M-multiplier on [0,1]MV.
(5) Given a fix real numbertand 0<t <1,letAt=([0,1],∧,∨,⊙,→,0,1) such that,for allx,y∈[0,1],
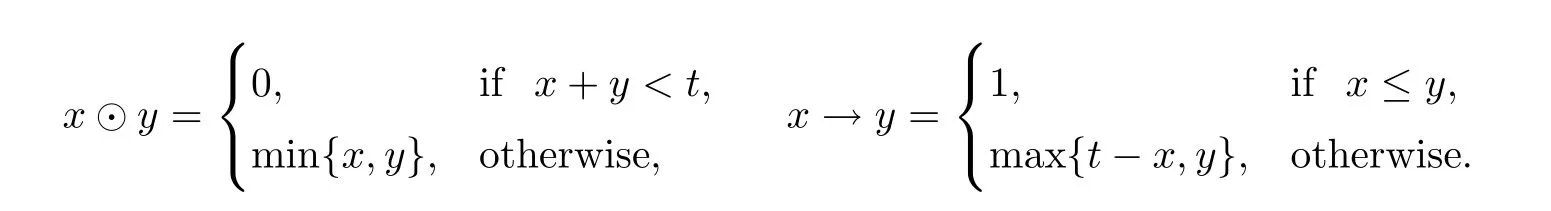
One can check that eachAtis a residuated lattice.Moreover,the mappingsf1(x)=0.3 ⊙x,are M-multipliers onAt.
(6) LetA1,A2be two residuated lattices.Then the Cartesian productA1×A2is a residuated lattice under pointwise operations;that is,(a,b) ⋄(c,d) :=(a⋄c,b⋄d),where⋄∈{∧,∨,⊙,→}.Assume thatf1is an M-multiplier onA1,f2is an M-multiplier onA2.Thenf((a1,a2)) :=(f1(a1),f2(a2)) is an M-multiplier onA1×A2.Moreover,ifA1=A2,theng1((a,b)) :=(f1(a),b) andg2((a,b)) :=(a,f1(b)) are two M-multipliers onA1×A1.
Lemma 3.3Letu,vbe two M-multipliers onA.Then the following statements are equivalent:
(1)u(x) ≤v(x),for anyx∈A;
(2)u(1) ≤v(1).
ProofProposition 2.3 (3) and Definition 3.1 directly indicate the result. □
Letu,vbe two M-multipliers onA.We defineu⊑vbyu(x) ≤v(x) for anyx∈A.Define (u⊓v)(x) :=u(x) ∧v(x),(u⊓⋆v)(x) :=(u(1) ∧v(1)) ⊙x,(u⊔v)(x) :=u(x) ∨v(x),(u⊗v)(x) :=(u(1) ⊙v(1)) ⊙x,(uv)(x) :=(u(1) →v(1)) ⊙x,and denote the set of all M-multipliers onAbyMM(A).Then we have the following results:
Theorem 3.4LetAbe a residuated lattice.ThenA≌(MM(A),⊓⋆,⊔,⊗,,idA,0A).
ProofLetu,v∈MM(A).Then (u⊓⋆v)(x⊙y)=(u(1)∧v(1))⊙(x⊙y)=x⊙(u⊓⋆v)(y)impliesu⊓⋆v∈MM(A).From Proposition 2.3 (6),we have that (u⊔v)(x⊙y)=u(x⊙y) ∨v(x⊙y)=(u(1) ⊙x⊙y) ∨(v(1) ⊙x⊙y)=x⊙(u⊔v)(y);that is,u⊔v∈MM(A).Then,together with Examples 3.2 (1) and (2),we can obtain that (MM(A),⊓⋆,⊔,idA,0A) is a bound lattice.Similarly,it is easy to check thatu(x) ⊗v(x),u(x)v(x) ∈MM(A) and that (MM(A),⊗,idA) is a commutative monoid.For anyu,v,w∈MM(A),by Lemma 3.3,we get thatu⊗v⊑w⇔(u(1) ⊙v(1)) ⊙x≤w(1) ⊙x⇔u(1) ⊙v(1) ≤w(1)⇔u(1) ≤v(1) →w(1)⇔u(1) ⊙x≤(v(1) →w(1)) ⊙x⇔u⊑vw.
Define a mappingφ:A→MM(A),φ(a)=fa(wherea∈A,fa∈MM(A)).According to the Examples 3.2 (3) and Lemma 3.3,we have thatφis well-defined.Assume thatf∈MM(A).Then there existsb∈Asuch thatf(x)=f(1) ⊙x=b⊙x=fb(x)=φ(b),and thusφis subjective.Suppose thata,b∈A,a≠bandfa=fb.Thena=fa(1)=fb(1)=b,which is a contradiction.Hence,φis injective.Moreover,for anya,b∈A,φ(a∧b)=(a∧b)⊙x=(fa(1)∧fb(1))⊙x=(fa⊓⋆fb)(x)=φ(a)⊓⋆φ(b).Similarly,φ(a∨b)=φ(a)⊔φ(b),φ(a⊙b)=φ(a) ⊗φ(b),φ(a→b)=φ(a)φ(b),φ(1)=idAandφ(0)=0A.ThereforeA≌(MM(A),⊓⋆,⊔,⊗,,idA,0A). □
Corollary 3.5LetAbe an MV-algebra,a BL-algebra,or a divisible residuated lattice.Then (MM(A),⊓,⊔,⊗,,idA,0A)=(MM(A),⊓⋆,⊔,⊗,,idA,0A) is an MV-algebra,a BLalgebra,or a divisible residuated lattice,respectively,and is isomorphic toA.
Definition 3.6Letf∈MM(A).Then
(1)fis called semi-idealised provided thatf(1) ∈G(A);
(2)fis called idealised provided thatf(1) ∈B(A).
Example 3.7(1) LetAbe the residuated lattice that of Example 3.2 (3).Thenfa(x)=a⊙xandfc(x)=c⊙xare semi-idealised M-multipliers onA.
(2) LetA={0,a1,a2,a3,a4,1},⊙,→and the Hasse diagram ofAbe defined as follows:

Then (A,∧,∨,⊙,→,0,1) is a residuated lattice andf(x)=a1⊙xis an idealised M-multiplier onA.
(3) LetZdenote the additive groups of integers,with the natural order,andn=(wherenis an integer andn≥2).If we definexi⊙xj=xmax{i+j-(n-1),0},xi→xj=xmin{(n-1)-i+j,n-1},xi∨xj=max{xi,xj},xi∧xj=min{xi,xj},then (n,∧,∨,⊙,→,0,1) is a residuated lattice.ConsiderAis the residuated lattices that of Example 3.2 (3),thenA×nis a residuated lattice andf((x,y))=(a,1) ⊙(x,y)is a semi-idealised M-multiplier onA×n.
(4) LetB=[0,1] be the real unit interval.Define ⊙and →onBas follows: for anyx,y∈B,

ThenB=([0,1],min,max,⊙,→,0,1) forms a residuated lattice.Meanwhile,ft(x)=t⊙xis a semi-idealised M-multiplier onB,wheretis a fixed number in [0,1].ConsiderAis the residuated lattice that of Item (2),theng((s,t))=(a3,1) ⊙(s,t) is an idealised M-multiplier onA×B.
Proposition 3.8Iffis an idealised M-multiplier onA,then,for anyx,y∈A,
(1)f(f(x))=f⊗f=f,(2)f(B(A)) ⊆B(A),
(3)f(x∧y)=f(x) ∧f(y),(4)f(x⊙y)=f(x) ⊙f(y),
(5)f(x→y)=f(1) ⊙(f(x) →y),(6)fis a closure operator,
(7)f(x∨y)=f(x) ∨f(y).
Moreover,(3) ⇔(4) ⇔(5).
ProofItems (1)–(6) are obvious and the mutual equivalence of (3),(4) and (5) are straightforward,by Proposition 2.3 (9) and Proposition 2.4 (1),(6)–(8). □
SettingFf(A) :={x|f(x)=x,x∈A},we can get the results below.
Lemma 3.9Letf∈MM(A).Then,
(1) iffis semi-idealised,then (Ff(A),⊓,∨,0,f(1)) is a bounded lattice (wherea⊓b=f(a∧b));
(2) iffis semi-idealised andAdivisible,orfis idealised,then (Ff(A),∧,∨,0,f(1)) is a bounded lattice;
(3) iffis semi-idealised,then (Ff(A),⊙,f(1)) is a monoid;
(4) iffis semi-idealised andAis anMV-algebra,thenFf(A) is an ideal ofA.
Proof(1) Iffis semi-idealised,then one can prove thatfis a closure operator and preserve ∨,which implies thatp∨q∈Ff(A) for anyp,q∈Ff(A).In fact,p∨qis the least upper bound ofp,qinFf(A).Suppose thatt∈Ff(A) andt≥p,q.Then there existx1,x2andx3such thatf(1) ⊙x1=t≥f(1) ⊙x2=p,f(1) ⊙x3=q,which implies thatt≥(f(1) ⊙x2) ∨(f(1) ⊙x3)=f(1) ⊙(x1∨x2)=p∨q;that is,t≥p∨q.Meanwhile,from the definition of ⊓,we obtain thatp⊓q∈Ff(A).Assume thats≤p,qands∈Ff(A).Then there isx4such thats=f(1) ⊙x4andf(1) ⊙x4≤f(1) ⊙x2,f(1) ⊙x3,which givess=f(1) ⊙x4=f(1) ⊙(f(1) ⊙x4) ≤f(1) ⊙((f(1) ⊙x2) ∧(f(1) ⊙x3))=f(1) ⊙(a∧b)=f(a∧b)=a⊓b.Hence,in combination with the fact thatfis isotone andf(0)=0,we can obtain that (Ff(A),⊓,∨,0,f(1)) is a bounded lattice.
(2) According to Proposition 2.4 (6) and 3.8 (3),we can obtain the result.Item (3) is obvious and item (4) is easily proven by Proposition 2.4 (12)–(13). □
Theorem 3.10Letf∈MM(A).Then,
(1) iffis semi-idealised,then (Ff(A),⊓,∨,⊙,,0,f(1)) is a residuated lattice (wherea⊓b=f(a∧b),ab=f(a→b) for anya,b∈Ff(A));
(2) iffis idealised,then (Ff(A),∧,∨,⊙,,0,f(1)) is a residuated lattice (whereab=f(a→b) for anya,b∈Ff(A));
(3) iffis semi-idealised andAis divisible,then (Ff(A),∧,∨,⊙,,0,f(1)) is a divisible residuated lattice (whereab=f(a→b) for anya,b∈Ff(A));
(4) iffis semi-idealised andAis an MV-algebra,then (Ff(A),∧,∨,⊙,,0,f(1)) is an MV-algebra.
Proof(1) By Lemma 3.9,we just need to prove thata⊙b≤ciffa≤bcfor anya,b,c∈Ff(A).Assume thata,b,c∈Ff(A) anda⊙b≤c.Then there existx1,x2,x3∈Asuch thata=f(1) ⊙x1,b=f(1) ⊙x2,c=f(1) ⊙x3,which concludes thata⊙b≤cifff(1) ⊙x1⊙f(1) ⊙x2≤f(1) ⊙x3ifff(1) ⊙x1≤f(1) ⊙x2→f(1) ⊙x3.Thus,together with Proposition 2.3 (3) and Proposition 2.4 (1,8),we obtain thata=f(1)⊙x1≤f(1)⊙(f(1)⊙x2→f(1) ⊙x3)=f(1) ⊙(b→c)=f(b→c)=bc.Conversely,ifa≤bc,then we have thatf(1)⊙x1≤f(1)⊙(f(1)⊙x2→f(1)⊙x3),which implies thatf(1)⊙x1≤f(1)⊙x2→f(1)⊙x3.Thus we can get thatf(1) ⊙x1⊙f(1) ⊙x2≤f(1) ⊙x3;that is,a⊙b≤c.Therefore,(Ff(A),∧,∨,⊙,,0,f(1)) is a residuated lattice.
(2) The proof is similar to that of item (1).
(3) According to Lemma 3.9 (2) and item (2),we only need to prove the divisibility ofFf(A).Assume thata,b∈Ff(A).Then there existx1,x2∈Asuch thata=f(1) ⊙x1,b=f(1) ⊙x2anda∧b=(f(1) ⊙x1) ∧(f(1) ⊙x2)=(f(1) ⊙x1) ⊙(f(1) ⊙x1→f(1) ⊙x2)=f(1) ⊙x1⊙(f(1) ⊙(f(1) ⊙x1→f(1) ⊙x2))=a⊙(ab).Hence the statement holds.
(4) From Definition 2.2 (5),Proposition 2.3 (5) and Item (2),the result is straightforward.□
From Lemma 3.9 and Proposition 3.8,it is easy to find that the image off(namely,Ff(A)) is a lattice ideal ofA,whenAis a residuated lattice andfis idealised.In Example 3.7 (2),B(A)={a1,a3},fa1=a1⊙xandfa3=a3⊙xare idealised M-multipliers,andFfa1(A)={0,a1,a4},Ffa3(A)={0,a3} are lattice ideals ofA.In fact,for any semi-idealised M-multiplierfon a residuated latticeA,Ff(A) is not always a lattice ideal.In Example 3.2 (3),G(A)={a,c},fc(x)=c⊙xandfa(x)=a⊙xare semi-idealised,butFfc(A)={0,a,c} is not lattice ideal,andFfa(A)={0,a} is lattice ideal.In fact,for anMV-algebraA,G(A)=B(A)indicates thatfis semi-idealised ifffis idealised.We have,for anMV-algebraAwherefis semi-idealised,Ff(A) is an ideal ofA,which implies thatFf(A) is a lattice ideal ofA.The above facts bolster that of our concept of Definition 3.6.
In what follows,we will present the fact thatfis a total multiplier wheneverf∈MM(A)andf(1) ∈B(A).A total multiplier is a special partial multiplier (that is defined in [3] and is consistent with the definition that follows,whenAis a BL-algebra or an MV-algebra).We denote the set of all down-sets ofAbyD(A);that is,D(A)={D⊆A|x≤y,y∈Dimpliesx∈D},↓a={x∈A|x≤a}.
Definition 3.11LetAbe a residuated lattice.A mappingh:DA(whereD∈D(A)) is called a partial multiplier onAprovided thathsatisfies the following conditions:
(M1)h(e⊙x)=e⊙h(x) for everye∈B(A) andx∈D,
(M2)x⊙(x→h(x))=h(x) for everyx∈D,
(M3) ife∈B(A) ∩D,thenh(e) ∈B(A),
(M4)e∧h(x)=h(e) ∧xfor everyx∈Dande∈B(A) ∩D.
In fact,(M2) ⇔(M2′) :h(x) ≤x,wheneverAis a divisible residuated lattice,BL-algebra or MV-algebra.A partial multiplierhis said to be a total multiplier (simplify,T-multiplier),if the domain ofhisA.Without ambiguity,in what follows we use multiplier instead of partial multiplier.
Example 3.12(1)idAand0(h(x)=0,x∈A) are both M-multipliers and T-multipliers onA.
(2) LetAbe a residuated lattice,D∈D(A) anda∈B(A).If a mapha:AAis defined byha(x)=a∧xfor anyx∈A,thenhais a T-multiplier onA.Moreover,ha|D:DAis a partial multiplier onA.We say such multipliers are principal.
(3) LetAbe the residuated lattice of Example 3.2 (3) (in fact,it is not divisible (sinceb=b∧cc⊙(c→b)=c⊙b=a)).Define a maphc:↓cAbyhc(x)=c⊙(c→x) for anyx∈↓c.Thenhcis a partial multiplier onA,but it is not principal.
(4) LetBandA×Bbe the residuated lattices of Example 3.7 (4),D=[0,0.5] ⊆BandD1={0,a1,a3,a4}.Then the functionh:DB,x0.2 ∧xis a partial multiplier onBand the mappingf:D1×BA×B,(x,y)(a3,1) ∧(x,y) is a partial multiplier onA×B.Moreover,it is easy to verify that the M-multipliergin Example 3.7 (4) is a T-multiplier onA×B.
Remark 3.13Indeed,by the Definition 3.11,we have that each T-multiplier on a residuated latticeAis a particular M-multiplier.Thus the properties and results of M-multipliers always hold for T-multipliers on residuated lattices.However,M-multipliers on residuated lattices are not always T-multipliers;see examples that follow.
Example 3.14(1) LetA={0,a,b,1},0<a <b <1 and ⊙,→be defined as follows:
Then (A,∧,∨,⊙,→,0,1) is a residuated lattice.Moreover,one can easily check that the mapfa(x) :=a⊙xonAis an M-multiplier,but not a T-multiplier.
(2) LetAbe the residuated lattice of Example 3.2 (3).Then the maphc:↓cA,hc(x)=c⊙(c→x) for anyx∈↓cis a partial multiplier onA,however,it cannot be obtained by an M-multiplier restricted to a down-set (such as ↓c) ofA.
Theorem 3.15LetAbe a residuated lattice.Then,
(1)T M(A) (the set of all T-multiplier onA) is a Boolean center ofMM(A),
(2)T M(A)≌B(A) and the following commutate diagram hold:
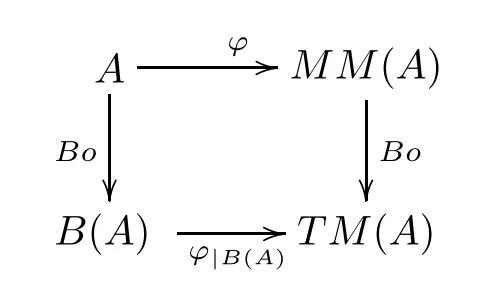
(whereBois a mapping that assigns a residuated latticeAto its Boolean center,andφis the map that of Theorem 3.4).
Proof(1) It follows,by Remark 3.13,that every T-multiplier is an M-multiplier.ThenT M(A) ⊆MM(A).Assumingv(x) ∈T M(A),then we have thatv(x)=v(1) ⊙xandv(1) ∈B(A),(v⊔v*)(x)=v(x) ∨v*(x)=v(x) ∨(v0)(x)=(v(1) ⊙x) ∨((v(1) →0) ⊙x)=(v(1)∨(v(1))*)⊙x=1⊙x=x=idA.Similarly,(v⊓⋆v*)(x)=(v(1)∧(v(1))*)⊙x=0.Hencev(x) ∈B(MM(A));that is,T M(A) ⊆B(MM(A)).Conversely,iff∈B(MM(A)),then one can easily check thatf⊓⋆f*=0andf⊔f*=idA,which implies thatf(1) ∧(f(1))*=0 andf(1) ∨(f(1))*=1;that is,f(1) ∈B(A).Thusf(x)=f(1) ∧ximpliesf∈T M(A).ThenT M(A)=B(MM(A)),andT M(A) is a Boolean center ofMM(A).
(2) SinceB(A) is a Boolean center ofAandT M(A) is a Boolean center ofMM(A),then,together with the proof of Theorem 3.4,T M(A)≌B(A) and the statements of item (2) hold.□
Theorem 3.15 shows that T-multipliers on A are completely determined by the Boolean elements of residuated lattices.From 3.12–3.15,we realize that the M-multipliers and partial multipliers on A not only have some similarities,but also some differences.Thus we focus on partial multipliers the domain of which may be not equivalent toA.If dom(h)=A,then we denotehby.For anyD∈D(A),we denote thatM(D,A)={h:DA|his a partial multiplier onA}.For anyD1,D2∈D(A) andhi(x) ∈M(Di,A),i=1,2,we define(h1⊔h2)(x) :=h1(x)∨h2(x),(h1⊓h2)(x) :=h1(x)∧h2(x);(h1⊙h2)(x) :=h1(x)⊙(x→h2(x)),(h1h2)(x) :=x⊙(h1(x) →h2(x)).The set of all partial multipliers onAis denoted byM(A) :=∪D∈D(A)M(D,A).
Theorem 3.16LetAbe a residuated lattice.Then (M(A),⊓,⊔,⊙,,idA,0) is a residuated lattice.
ProofIn fact,h1⊔h2,h1⊓h2,h1⊙h2,h1h2∈M(D1∩D2,A),for anyhi∈M(Di,A),i=1,2.We just check thath1⊙h2∈M(D1∩D2,A) and other statements can be similarly obtained.Letx∈D1∩D2,e∈B(A).Then (M1) (h1⊙h2)(e⊙x)=h1(e⊙x)⊙(e⊙x→h2(e⊙x))=e⊙h1(x) ⊙(e⊙x→e⊙h2(x))=h1(x) ⊙e⊙(x→h2(x))=e⊙(h1⊙h2)(x).(M2) Since (x→h1(x)) ⊙(x→h2(x)) ≤x→(x⊙(x→h1(x)) ⊙(x→h2(x))),we obtain that (h1⊙h2)(x)=h1(x) ⊙(x→h2(x))=x⊙(x→h1(x)) ⊙(x→h2(x)) ≤x⊙[x→(x⊙(x→h1(x)) ⊙(x→h2(x)))]=x⊙[x→(h1⊙h2)(x)].Taking this together withx⊙[x→(h1⊙h2)(x)] ≤(h1⊙h2)(x),we can obtain thatx⊙[x→(h1⊙h2)(x)]=(h1⊙h2)(x).From (M2),the commutativity of ⊙onM(A) is clear.Moreover,Proposition 2.4 (8)–(9),(11)directly indicates (M3) and (M4).The rest of the proof is analogous to the standard proof.□
Definition 3.17A nonempty subsetD⊂Ais called regular if,for everyx,y∈Asuch thatx∧e=y∧efor everye∈D∩B(A),we have thatx=y.
Definition 3.18Leth1,h2,hbe multipliers onA.
(1) We say thath2extendsh1(writeh1h2) provided that dom(h1) ⊆dom(h2) andh2|dom(h1)=h1.
(2)his called maximal,provided thathcannot be extended to a strictly larger domain.We denote thatR(A)={D|Dis a regular subset ofA},thatRD(A)={D|Dis both a regular subset and down set ofA},andMr(A)={h|h∈M(A),dom(h) ∈RD(A)}.
Lemma 3.19LetAbe a residuated lattice.Then,
(1)D1,D2∈RD(A) impliesD1∩D2∈RD(A),
(2)Mr(A) is a subalgebra (residuated lattice) ofM(A),
(3) ifh1,h2∈M(A),h∈Mr(A) andhh1,hh2,thenh1,h2coincide on the dom(h1) ∩dom(h2),
(4) everyh∈Mr(A) can be extended to a maximal multiplier.Namely,for each principal multiplierha,dom(ha) ∈RD(A),there is a uniquely T-multipliersuch thatand every non-principal multiplier can be extended to a maximal non-principal one,
(5)θAis a congruence onMr(A).(The relationθAonMr(A) be defined by (h1,h2) ∈θAiffh1,h2coincide on dom(h1) ∩dom(h2)).
ProofItems (1) and (3)–(4) are easy to prove by Definitions 3.17–3.18.The proof of (2)is similar to that of Theorem 3.16.Therefore,here we only prove item (5).The reflexivity and the symmetry ofθAare clear.Let (h1,h2),(h2,h3) ∈Mr(A) and assume that (h1,h3)r(A).Then there existsp∈dom(h1)∩dom(h3) such thath1(p)≠h3(p).From dom(h2) ∈RD(A),we obtain somee∈dom(h2)∩B(A) ande∧h1(p)≠e∧h3(p) ⇐⇒h1(e⊙p)≠h3(e⊙p).However,e⊙p≤p,eimpliese⊙p∈dom(h1) ∩dom(h2) ∩dom(h3) andh1(e⊙p)=h3(e⊙p).This is a contradiction.Hence,θAis an equivalence relation onMr(A).Let (h1,h2),(h3,h4) ∈Mr(A)andz∈∩idom(hi).Then (h1h3)(z)=z⊙(h1(z) →h3(z))=z⊙(h2(z) →h4(z))=(h2h4)(z) implies thatθAis compatible with.Similarly,the compatibility ofθAwith ⊓,⊔,⊙is easy to check.Therefore,θAis a congruence onMr(A). □
Example 3.20(1) LetAbe the residuated lattice in Example 3.2 (3).Define some maps as follows:
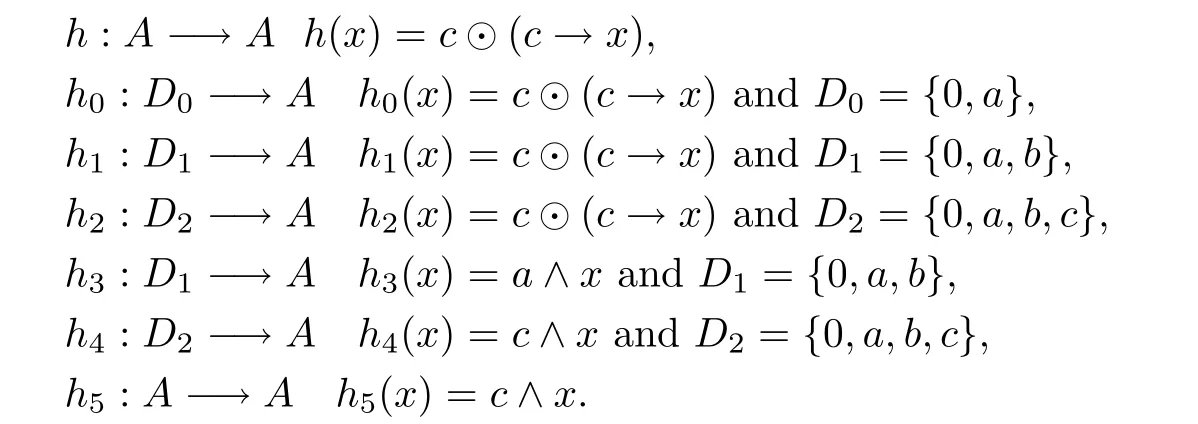
One can easily check thath0,h1,h2,h3andh4are multipliers and thath,h5are not multipliers.However,h|D2=h2,h5|D2=h4.Moreover,andh2cannot be extended to any multipliers.
(2) LetAbe the residuated lattice of Example 3.7 (2).ThenB(A)={0,1,a1,a3}.SettingD1={0,a1,a3,a4},D2={0,a1,a2,a3,a4},we have thatB(A) ∩D1=B(A) ∩D2,and,for everyp,q∈Aandp≠q,there exists an elemente∈B(A) ∩D1such that.HenceD1,D2∈RD(A).Moreover,define some maps as follows:
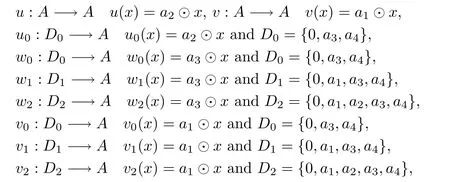
Thenu0,w0,w1,w2,v0,v1,v2andvare multipliers onA,butuis not a multiplier.Moreover,we have thatandu0cannot be extended to any multipliers.In fact,it is obvious thatw0,w1,w2,v1,v2,v∈Mr(A),u0is a maximal non-principal multiplier onAand thatvis the unique T-multiplier onAwhich is extended byv1,v2.Meanwhile,w0,w1,w2can be extended to a unique T-multiplierw:AA,w(x)=a3⊙xonA.
(3) LetA×Bbe the residuated lattice in Example 3.7 (4).SetD0,D1,D2as the down-sets in Item (2).ThenD1×B,D2×B∈RD(A×B).Now,considering the following mapping:
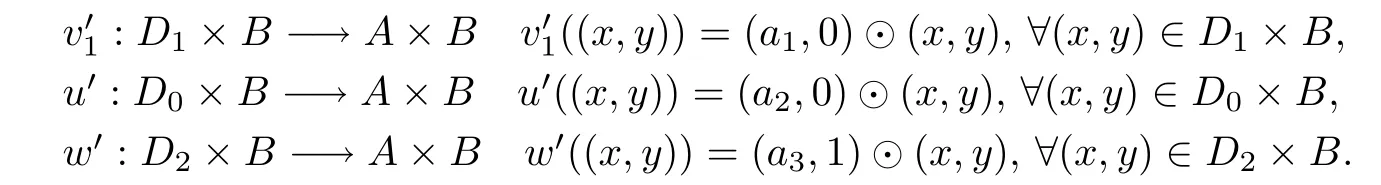
Then,u′,w′are multipliers onA×Band′∈Mr(A×B).Moreover,can be extended to a uniqueT-multiplierv′:A×B→A×B,v((x,y))=(a1,0)⊙(x,y) onA×B(that is,),butu′is a maximal non-principal multiplier onA×Band cannot be extended.Furthermore,it is clear thatB(A×B)={(0,0),(0,1),(1,0),(1,1),(a1,0),(a1,1),(a3,0),(a3,1)},so we can obtain thatpt,i:Di×BA×B,(x,y)t⊙(x,y) is a multiplier onA×Bandpt,i∈Mr(A×B),wheret∈B(A×B) andi=1,2.

Lemma 3.21Letbe defined byfor everya∈B(A).Then,

Definition 3.23A residuated latticeGis called a residuated lattice of fractions ofA(writeA≺G) provided that it satisfies that:
(1)B(A) is a subalgebra ofG,
(2) for everya,b,s∈G,a≠bthere existse∈B(A) such thate∧a≠e∧bande∧s∈B(A),
(3) for everya∈G,e∈B(A) such thate∧a∈B(A),ift∈B(A) andt≤e,thent∧a∈B(A).
Definition 3.24Mis called the maximal residuated lattice of quotients ofAprovided thatA≺M,and for each residuated latticeGwithA≺G,there is a monomorphismi:GMof residuated lattices.
Lemma 3.25LetA≺G.Then,for eacha,b∈G,a≠band any finite sequences1,···,sn∈G,there existse∈B(A) such thate∧a≠e∧bande∧si∈B(A) fori=1,2,···,n(n≥2).
ProofBy Definitions 3.23 (1) and (2) and mathematical induction,it is easy to prove.□
Lemma 3.26LetA≺G,a∈G.ThenDa={e|e∈B(A),e∧a∈B(A)} ∈D(B(A)) ∩R(A).
ProofObviously,Da∈D(B(A)).Assume thatp,q∈A,p≠qande∧p=e∧qfor alle∈Da∩B(A).ThenA≺G,and there isd∈B(A) such thatd∧a∈B(A) (namely,d∈Da∩B(A)) andd∧p≠d∧q,which is a contradiction.HenceDa∈R(A). □
Theorem 3.27A′′is the maximal residuated lattice of quotients ofA.

(4) Proof of the maximality ofA′′.LetA≺G(G is a residuated lattice).ThenB(A) ⊆B(G).Fort∈G,Dt={e∈B(A)|e∧t∈B(A)} ⊆D(B(A)) ∩R(A).It is easy to check thatht:DtA,ht=t∧xis a multiplier.If we definei:GA′′,i(t)=[ht,Dt] for everyt∈G,theni(0)=0.For anyt,s∈Gandx∈Dt∩Ds,(i(t)⊙i(s))(x)=(t∧x)⊙(x→s∧x)=t⊙x⊙(x→s∧x)=t⊙[x⊙(x→s∧x)]=t⊙[x⊙(1 ⊙x→s⊙x)]=t⊙[x⊙(1 →s)]=t⊙(x⊙s)=t⊙(x∧s)=(t∧s)∧x=i(t⊙s)(x),and (i(t)i(s))(x)=x⊙(i(t)(x) →i(s)(x))=x⊙(ht(x) →hs(x))=x⊙(t∧x→s∧x)=x⊙(x⊙t→s⊙x)=x⊙(t→s)=i(t→s)(x).Similarly,i(t) ∧i(s)=i(t∧s),i(t) ∨i(s)=i(t∨s).In fact,iis injective.Suppose thatt,s∈Gandi(t)=i(s).Then [ht,Dt]=[hs,Ds];that is,ht(x)=hs(x) for anyx∈Dt∩Ds,i.e.,t∧x=s∧x.Ifts,this,together with Lemma 3.25 andA≺G,gives that there ise∈B(A)such thate∧t,e∧s∈B(A) ande∧t≠e∧s.However,e∧t,e∧s∈B(A) implies thate∈Dt∩Ds,which is a contradiction.Therefore,the results hold. □
Corollary 3.28A′′is the maximal □-algebra of quotients ofAprovided thatAis a□-algebra (where □∈{MV,BL,MT L}).
Example 3.29(1) LetA={0,1} be a Boolean algebra (a special residuated lattice).ThenA≺AandB(A)=A.Clearly,Ais a unique element belonging toR(A);that is,the domain ofh∈Mr(A) must be equivalent toA.0A:AA,x0 andidA:0A:AA,xx(for anyx∈A) are all elements that belong toMr(A).Obviously,0A,idAbelongs to a different congruence class,andB={0A,idA} is a residuated lattice.Obviously,for anyMthat satisfies Definition 3.24,we haveM≌A.Moreover,A′′={[0A,A],[idA,A]} is clear andA′′≌A.
(2) LetAbe the residuated lattice of Example 3.7 (2).By Example 3.20 (2),we haveD1,D2,A∈R(A) andw0,w1,w2,w,v1,v2,v∈Mr(A).It is clear that0A|D1,0A|D2,0A,idA|D1,idA|D2,idA∈Mr(A) and [0A,A]={0A|D1,0A|D2,0A},[idA,A]={idA|D1,idA|D2,idA},[w,A]={w0,w1,w2,w},[v,A]={v1,v2,v}.One can check thatA′′=({[0A,A],[idA,A],[v,A],[w,A]},⊓,⊔,⊙,,⊥,⊤) is not only a residuated lattice,but also the maximal residuated lattice of quotients ofA,where the rule of ⊓,⊔,⊙,,⊥,⊤is just as defined in Lemma 3.21.
(3) LetA×Bbe the residuated lattice in Example 3.20 (3),which obviously has an infinite number of elements.ThenD1×B,D2×B,A×B∈RD(A×B) andB(A×B)={(0,0),(0,1),(1,0),(1,1),(a1,0),(a1,1),(a3,0),(a3,1)}.It is clear that0A×B((x,y))=(0,0)andidA×B((x,y))=(x,y) are multipliers and that they belong toMr(A×B).Meanwhile,we have that (A×B)′′=({[0A×B,A×B],[idA×B,A×B],[pt,i,A×B] },⊓,⊔,⊙,⊥,⊤) is a residuated lattice,wheret∈B(A×B),i=1,2,3,D3=A,pt,iis the multiplier onA×Bof Example 3.20 (3).Moreover,it is easy to check that (A×B)′′is the maximal residuated lattice of quotients ofA×B,by the same method of Theorem 3.27.Moreover,if we have thatPBis the set of all subsets ofB,thenPBis not only a residuated lattice,but also a complete Boolean algebra,soA×PBis also a residuated lattice andB(A×PB) has infinite members,which implies that there are infinite multipliers belonging toMr(A×PB) (since,at least,such multipliers areh(x,y)=t⊙(x,y) ∈Mr(A×PB),wheret∈B(A×PB)).Hence,one can check that (A×PB)′′,constructed in the same way as Theorem 3.27,forms the maximal residuated lattice of quotients ofA×PB,which has an infinite element.
4 Implicative Multipliers on Residuated Lattices
In this section,we discuss the relation of M-multipliers,T-multipliers and PI-multipliers,and present that the algebraPIM(A) of PI-multipliers onAis isomorphic to the algebraMM(A) of M-multipliers onAunder dual-order.
Definition 4.1A mappingg:A→Aon a residuated latticeAis said to be an implicative multiplier (simplify,I-multiplier) provided that it satisfiesg(x→y)=x→g(y) for allx,y∈A.
Definition 4.2Letgbe an I-multiplier on a residuated latticeA.Thengis said to be
(1) an isotone I-multiplier provided thatx≤yimpliesg(x) ≤g(y) for anyx,y∈A;
(2) an idempotent I-multiplier provided thatg(g(x))=g(x) (that is,g2=g) for anyx∈A.
Example 4.3(1)idAandg(x)=1 for anyx∈A(simplify,1) are I-multipliers onA.
(2)gp(x)=p→xis an I-multiplier onA,wherep∈A.gp(x) is called a principal I-multiplier (simplify,PI-multiplier) onAand every PI-multiplier is isotone.
(3) LetA={0,a,b,1},0<a <b <1 and ⊙,→be defined as follows:

Then (A,∧,∨,⊙,→,0,1) is a residuated lattice.Now,we define a mapgonAas follows:
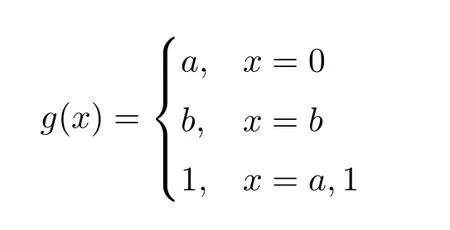
One can check thatgis an I-multiplier onA,but not isotone.
(4) LetAbe the residuated lattice of Example 3.2 (3),and defineg,gbonAas follows:
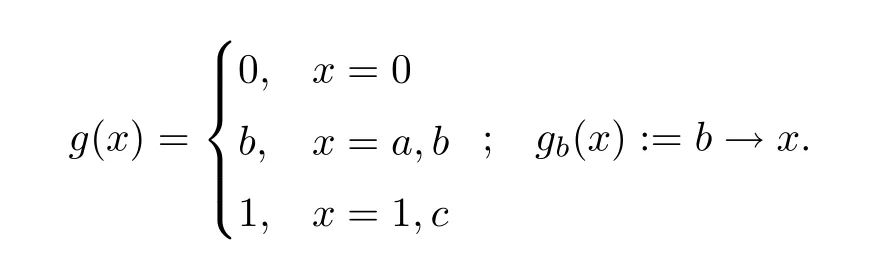
Thengis an isotone and idempotent I-multiplier onA.gb(x) is an isotone I-multiplier,but not idempotent.
(5) LetAbe the residuated latticeAtin Example 3.2 (5).Thenis an isotone I-multiplier onAt,but not idempotent.However,whenAis the residuated lattice of Example 3.7 (4),we can get that the mappinggt(x)=t→xis an isotone and idempotent I-multiplier,wheretis a fixed number in an open interval (0,1).
Denote the set of all I-multipliers onAbyIM(A) and all PI-multipliers byPIM(A).
Lemma 4.4Letf∈MM(A).Then there exists an I-multiplierg∈PIM(A) such that(f,g) forms a Galois connection.
ProofLetf∈MM(A).Thenf(y)=f(1) ⊙y,for anyy∈A.Assume thatf(y) ≤x.Then we can get thatf(1) ⊙y≤xiffy≤f(1) →x=gf(1)(x) (wheregf(1)(x) ∈PIM(A)).Taking this together with Proposition 2.3 (3) and Example 4.3 (2),we easily obtain that(f,gf(1)) forms a Galois connection. □
According to Proposition 3.13,Theorem 3.15 (2),Example 4.3 (3) and Lemma 4.4,it is easy to get the following diagram:
Proposition 4.5Leta,b∈A.Then,for anyx,y∈A,
(1)ga(x∧y)=ga(x) ∧ga(y),
(2)a≤biffgb≤ga,
(3)abimpliesga≠gb,
(4)ga°gb=ga⊙b=gb°ga,
(5)ga⊓gb=ga∨b,
(6) ifAis a BL-algebra,thenga⊔gb=ga∧b.
ProofBy Lemma 4.4,Lemma 3.3 and Proposition 2.3 (3),(7),items (1)–(3) are obvious.Items (4)–(6) are straightforward,by Proposition 2.3 (5),(7),(10). □


Corollary 4.7Let (A,∧,∨,⊙,→,0,1) be aBL-algebra (or anMV-algebra).Then(PIM(A),≤op,⊓op,⊔op,°,⋄,1,idA)≌(MM(A),⊑,⊓,⊔,⊗,,0A,idA)≌A(≤op:=≥,⊓op:=⊔,⊔op:=⊓).
ProofProposition 4.5 (5)–(6),Corollary 3.5 and Theorem 4.6 directly indicate the results.□
Corollary 4.8Let (A,∧,∨,*,0,1) be a Boolean algebra.Then (PIM(A),⊓,⊔,,g1,g0)forms a Boolean algebra,which is isomorphic to (A,∨,∧,*,0,1) (wherega:=ga*).
ProofBy Proposition 2.4 (1)–(5) and Proposition 2.3 (7),we can get thatga(x ⋆y)=ga(x)⋆ga(y),ga⊔ga*=g0andga⊓ga*=g1,where⋆∈{∧,∨,⊙,→}.From this,together with Proposition 4.5 (5-6) and Theorem 4.6,we conclude that the result hold. □
Finally,we present some examples to illustrate the relation betweenMM(A) andPI(A).
Example 4.9(1) LetAbe the residuated lattice of Example 3.2 (3).Define mapsf,g,honAbyf(x)=a⊙x,g(x)=b⊙x,h(x)=c⊙x,respectively.ThenMM(A)={0A,f,g,h,idA}and0A≤f≤g≤h≤idA.Moreover,we have the following:
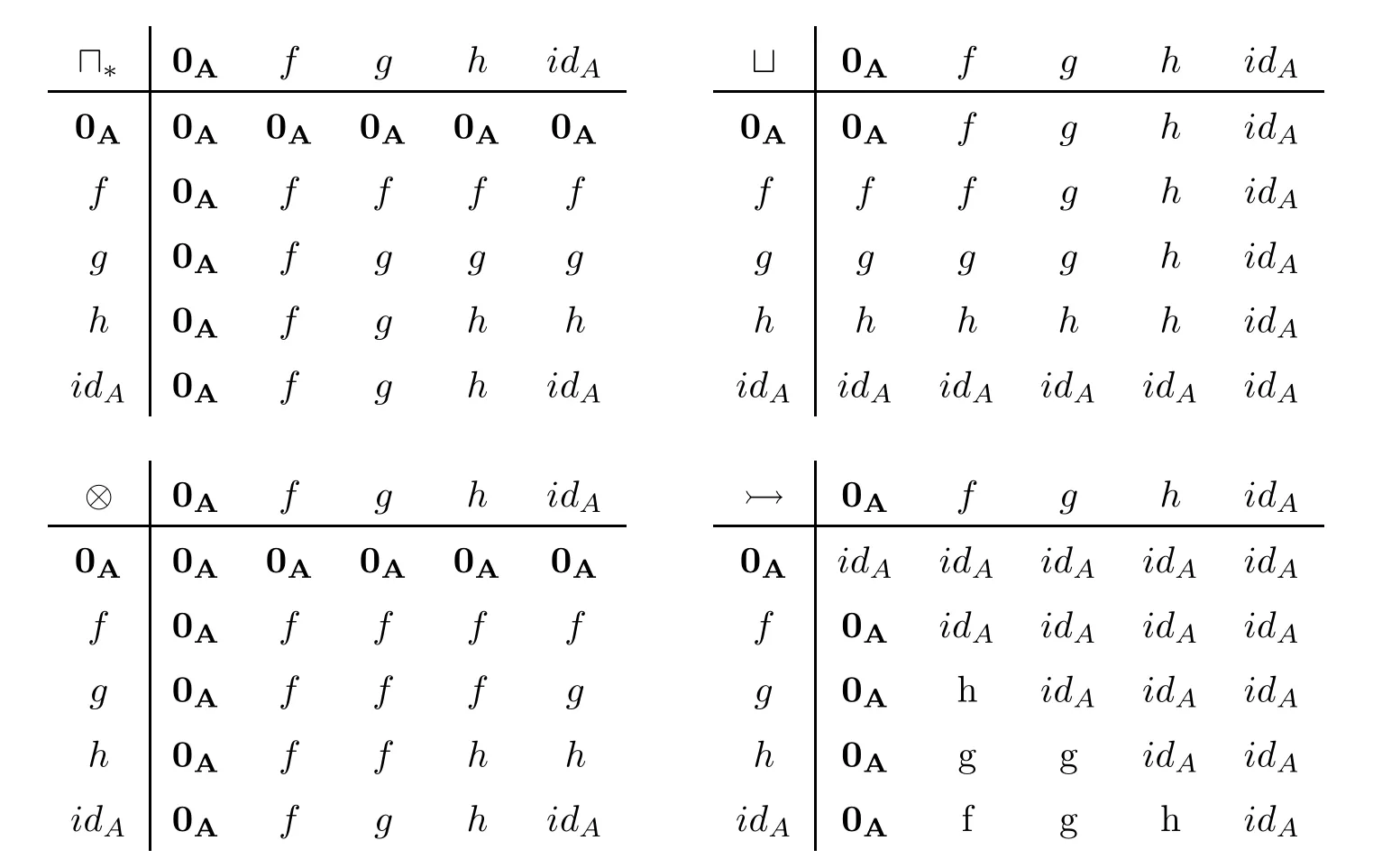
Hence,(MM(A),⊑,⊓,⊔,⊗,,0A,idA) is a residuated lattice.
Obviously,PIM(A)={idA,ga,gb,gc,1} andidA≤gc≤gb≤ga≤1;that is,1 ≤opga≤opgb≤opgc≤opidA.Meanwhile,we have


5 Conclusions
In this paper,motivated by previous research on multipliers on MV-algebras,BE-algebras and BL-algebras,we extended the concept of multipliers to the more general fuzzy structures,namely residuated lattices.The paper has introduced some multipliers on residuated lattices and investigated the relations between them.We concluded that the setMM(A) of all multiplicative multipliers on a residuated latticeAis a residuated lattice and is isomorphic toA.Each semi-idealised M-multiplier onMV-algebraAcorresponds to an ideal ofA.Moreover,the setT M(A) of all total multipliers onAis a Boolean subalgebra ofMM(A) and is isomorphic toB(A).Meanwhile,the paper has shown thatA′′is the maximal residuated lattice of the quotient for a residuated latticeA.Finally,the paper has shown that the algebraPIM(A) of PI-multipliers on a residuated latticeAis isomorphic toMM(A) under the opposite order.
猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- RELAXED INERTIAL METHODS FOR SOLVING SPLIT VARIATIONAL INEQUALITY PROBLEMS WITHOUT PRODUCT SPACE FORMULATION*
- PHASE PORTRAITS OF THE LESLIE-GOWER SYSTEM*
- A GROUND STATE SOLUTION TO THE CHERN-SIMONS-SCHRÖDINGER SYSTEM*
- ITERATIVE METHODS FOR OBTAINING AN INFINITE FAMILY OF STRICT PSEUDO-CONTRACTIONS IN BANACH SPACES*
- A NON-LOCAL DIFFUSION EQUATION FOR NOISE REMOVAL*
- BLOW-UP IN A FRACTIONAL LAPLACIAN MUTUALISTIC MODEL WITH NEUMANN BOUNDARY CONDITIONS*
