任洁,彭建文

(重庆师范大学数学科学学院,重庆 401331)

1.引言

在多目标优化中,我们要对多个目标函数同时最小化或同时最大化,由于单个点一般不可能使得所有给定的目标函数同时取得最优值,因此,人们往往使用Pareto最优性的概念.这类优化问题在许多领域都有应用,包括工程、设计、选址问题、空间探索、统计学、管理科学、环境分析等领域.

标量化方法[1]是将多目标优化问题转化为单目标的数学规划问题进行求解,是求解多目标优化问题最有效的方法之一.特别地,所谓的加权和方法将目标的线性组合作为标量重构的目标函数.然而,当原问题是非凸的多目标优化问题时,可能无法得到该问题特定的Pareto最优解.为了克服这一缺点,Ogata等人[2]还提出了次线性标量化方法.经典的求解多目标优化问题的加权和方法的缺点是事先需要未知的权重参数来得到期望的解.另一种不涉及标量化的求解多目标优化问题的方法是基于启发式的方法[3],在这种情况下,不一定能保证此类算法所产生的点列收敛到多目标优化问题的Pareto最优解.

近年来,许多研究人员提出了一些不需要任何先验信息的多目标优化技术: 例如最速下降法[4]、牛顿法[5]、拟牛顿法[6]、投影梯度法[7]和共轭梯度法[8],这些方法是对相应的单目标优化方法的推广.在这些方法中,步长的选择使目标函数值在每次迭代中都减小.但是,由于目标函数数量的增加,Armijo条件变得更加严格,可能导致更小的步长.然而,在非单调线搜索方法中,允许某些函数值的增加.正如一些研究人员指出,单目标优化的非单调技术可以增加找到全局最优解的可能性;此外,它们可以提高收敛速度(见文[9]).将非单调技术应用于复杂的非线性单目标优化问题时,已有令人鼓舞的数值结果(见文[9-11]).最近,Mita[12]等人将非单调线搜索方法由单目标优化问题推广到多目标优化问题,从而提出了求解无约束多目标优化问题的非单调线搜索的最速下降法和牛顿法,并建立了它们的全局收敛性.ZHANG和Hager[11]提出并分析了求解无约束单目标优化问题的非单调线搜索方法.Fliege等人[5]建立了求解多目标优化问题的单调牛顿法的局部超线性收敛率.基于此,我们将给出求解多目标优化问题的非单调牛顿法[12]的全局收敛性及其局部超线性收敛率的分析.

本文剩下的内容如下: 在第2节,我们给出了一些符号说明和有关Pareto最优性和Pareto平稳性的概念.在第3节,我们陈述了文[12]提出的求解无约束多目标优化问题的非单调牛顿法.在第4节,我们在适当的假设条件下给出了求解多目标优化问题的非单调牛顿法的全局收敛性.在第5节,我们建立了该算法的局部超线性收敛率.最后,我们在第6节中做出结论并提出未来研究的方向.

2.预备知识

3.非单调牛顿法

这一节,我们将回顾文[12]提出的求解多目标优化问题(2.1)的非单调牛顿法.

这里,对所有i=1,···,m,我们假设Fi是二阶连续可微的,且对∀x∈Rn,∇2Fi(x)是正定的.在这种情况下,对于给定x∈Rn,通过求解下面的无约束问题来计算搜索方向:

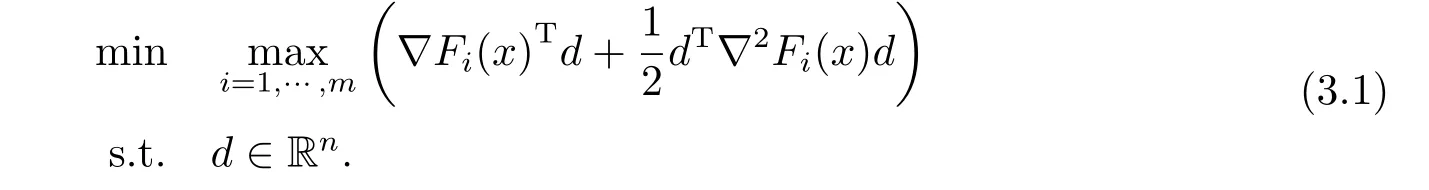
因为∇2Fi(x)是正定的,所以(3.1)的目标函数是强凸的.因此,用dN(x)表示其唯一最优解,用θN(x)表示其最优函数值,即

然后给出引理3.1的一个明显的结论.

推论3.1[12]1)x是多目标优化问题(2.1)Pareto平稳点,当且仅当θN(x)=0,或等价地,当且仅当dN(x)=0.

2)x不是多目标优化问题(2.1)的Pareto平稳点,当且仅当θN(x)＜0,或等价地,当且仅当dN(x)0.

对于F:Rn →Rm,在一个非平稳点x∈Rn,关于搜索方向dN(x)的Armijo法则为

其中δ∈(0,1),见文[5].

在这里,我们将使用由文[11]中单目标优化的非单调Armijo条件推广到多目标优化的非单调Armijo条件.

基于以上讨论,我们将回顾文[12](算法2、算法4)给出如下求解多目标优化问题(2.1)的非单调牛顿法(算法3.1):

算法3.1步1 取初始点x0∈Rn,参数δ∈(0,1),ρ∈(0,1),μ ＞0,η∈[0,1].令k=0,C0=F(x0),q0=1.

引理3.2[12]对于算法3.1的每次迭代k,则有F(xk)≤Ck ≤Ak.

在下一个命题中,说明了算法3.1是有定义的,因为总有一个满足非单调Armijo条件(3.10)的步长,以便生成迭代序列{xk}.

命题3.1[12]设xk是由算法3.1生成的序列,如果xk不是多目标优化问题(2.1)的Pareto平稳点,则存在一个步长αk ＞0满足非单调Armijo条件(3.10).

4.非单调牛顿法的全局收敛性

首先,我们给出由非单调牛顿法(算法3.1)生成的步长的一个下界.

条件4.1假设对∀i=1,···,m,∇Fi满足以下带有常数L的Lipschitz连续:

注4.1文[12]是将单目标优化的相关结论推广到多目标优化,进而证明了求解多目标优化问题的非单调牛顿法的全局收敛性(见文[12]的定理7).现在,下面我们将利用求解多目标优化问题的牛顿法的相关结论直接证明非单调牛顿法(算法3.1)的全局收敛性,假设条件更合理,结论更直接.

定理4.1假设对∀i=1,···,m,Fi(x)是下有界的,η ＜1,若条件4.1成立且存在常数c1＞0,使得

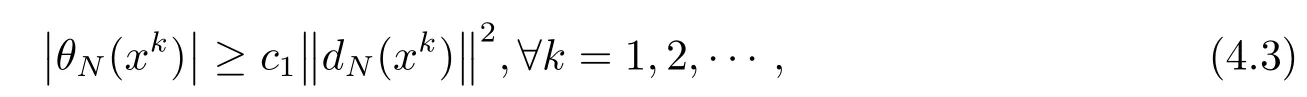
则由算法3.1生成的序列{xk}的每个极限点是多目标优化问题(2.1)的Pareto平稳点.

证首先,我们证明对所有i=1,···,m有

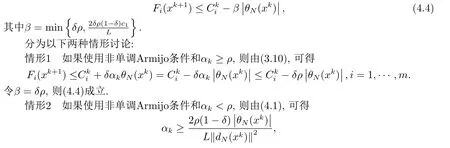
接下来,我们证明当k →+∞时,θN(xk)和‖‖dN(xk)‖‖都收敛到0.

命题4.1假设由算法3.1生成的序列{xk}是有界的,且它的极限点是多目标优化问题(2.1)的Pareto平稳点,假设存在常数a ＞0,使得对所有i=1,···,m和所有k,有

5.局部超线性收敛率

在此,我们将建立求解多目标优化问题(2.1)的非单调牛顿法的局部超线性收敛率.首先,我们需要陈述一个条件.

6.结论

针对文[12]中提出的求解无约束多目标优化问题的非单调牛顿法,在适当的条件下,我们证明了该算法生成的迭代序列的每一个极限点都是多目标优化问题的Pareto平稳点.在合理的假设下,建立了该算法的局部超线性收敛率.随着研究的深入,我们未来将会提出新的非单调技术和研究求解多目标优化问题的其他新的非单调算法.