肖 云，温瑞萍

（太原师范学院工程科学计算山西省高等学校重点实验室，山西晋中 030619）

0 引 言

矩阵填充问题假设当目标矩阵具有低秩或近似低秩的特性时，其能够对含有大量缺失元素的矩阵进行近乎完美的填充.填充一个未知的低秩或近似低秩采样矩阵是一个具有挑战性的问题.目前，矩阵填充在机器学习［1-2］、推荐系统［3］、图像处理［4］、控制理论［5］和计算机视觉［6］等数据科学领域中都有非常重要的应用.

在 2009 年，Candès和 Recht［7］建立了关于矩阵填充问题的凸优化模型：

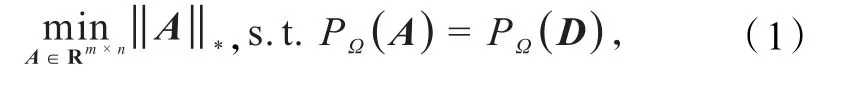
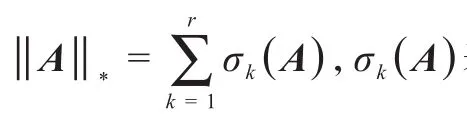
对于求解问题（1），通常算法中的每次迭代都需要计算一个m×n阶矩阵的奇异值分解（singular value decomposition，SVD）.近年来，基于核范数最小化的研究，有不少的成果.如文献［8］提出了一种易于实现的奇异值阈值算法（singular value thresholding，SVT），该算法可以得到具有低秩结构的最优解，并保证了填充矩阵的稀疏性，一定程度上节省了存储空间，可以有效地处理低秩的大规模矩阵填充问题.但当秩较大时，此算法收敛速度缓慢甚至效果不是很理想，在文献［9］给出了加速SVT算法.与此同时，Toh和Yun［10］提出了加速临近梯度算法（accelerated proximal gradient，APG）；Lin 等［11］提出了比APG算法速度快、精度高的增广拉格朗日乘子算法（augmented lagrange multiplier，ALM），该算法具有很好的操作性和收敛性，并且需要较小的存储空间.

由以上算法结果报告，SVD计算花费占去整个算法花费的80%以上，而Toeplitz矩阵的SVD具有较低的算法复杂度，且一个n×n阶的Toeplitz矩阵T ∈ Rn×n表达形式为

那是由2n-1个元素决定的，即表达式（2）的第一行和第一列元素.近年来，针对Toeplitz矩阵填充问题，方云兰和郑慧娆［12］研究了Toeplitz块矩阵填充的快速正交三角分解算法；于益华和李云翔［13］研究了基于快速小波变换的Toeplitz矩阵填充算法；Wang 和 Li［14-16］提出了 Toeplitz矩阵填充的均值算法、修正的ALM算法、保结构算法［16］；刘丽霞和王川龙［17］进一步提出了子空间算法；Wen 等［18］、Wen和Li［19］研究了逐步结构化的ALM算法以及l步结构化的ALM算法.

本文主要是基于均值的增广拉格朗日乘子算法（ALM based on mean value，MALM）算法，对中小型规模的低秩矩阵进行填充.为了减少MALM算法中频繁的数据传输量与结构化操作所增加的计算量，采用ALM算法，当迭代矩阵逐渐靠近目标矩阵时，开始对矩阵进行尾部修正并结构化，修正使迭代矩阵从数值上更加靠近目标矩阵，结构化使迭代矩阵与目标矩阵保持同样结构，可利用快速奇异值分解，从而减少迭代步数，缩短奇异值分解时间，节约算法的整体花费.同时给出了算法收敛性分析，并通过数值实验验证了算法的有效性.下面给出一些定义：

可见，Γ(A)是由矩阵A派生的Toeplitz矩阵.换句话说，∀A∈Rn×n，都可以通过结构化算子 Γ(·)转化为一个Toeplitz矩阵.

本文拟简单回顾ALM和MALM，并分别比较2种算法所具有的优缺点，介绍关于Toeplitz矩阵填充的尾端修正ALM算法（Tailed-modification ALM，l-TMALM）；运用核范数的性质给出新算法的收敛性分析；通过与l-MALM，MALM以及ALM算法作比较得出新算法的有效性.

符号说明.为方便起见，Rm×n表示的是m×n阶的实数矩阵.矩阵A的核范数用‖A ‖*表示，而‖A ‖F表示矩阵A的Frobenius范数.AT表示矩阵A的转置.对于一个Toeplitz矩阵A ∈ Rn×n，diag(A ，l)表示矩阵A的第l条对角线元素，l=-n+1，…，n-1.Ω⊂{ - n+1,…,n-1}是采样集，PΩ是相应矩阵在Ω上的投影算子，满足

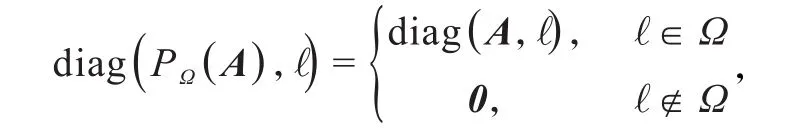
其中0是一个零向量.

1 相关算法

低秩Toeplitz矩阵的填充问题.为了方便比较，先简单回顾ALM算法，并将其应用到Toeplitz矩阵填充问题中.

1.1 ALM［11］

当问题（1）中的m=n时，即矩阵A，E，D ∈ Rn×n为Toeplitz矩阵时，求解式（1）的等价形式为

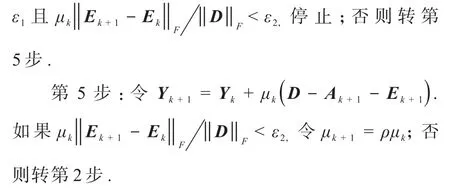
数值实验表明，ALM算法在理论和实际应用中均有较好的效果，且该算法迭代快，具有线性全局收敛速度，但奇异值分解时间较长，精度较低，收敛效果不是很理想.

1.2 对偶算法（dual algorithm）［21］

对偶算法是为了通过其对偶性求解问题（4），即首先要解决的问题是

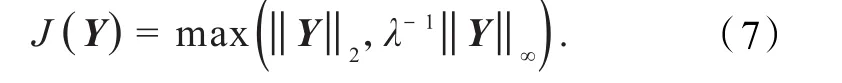
对于最优增广拉格朗日乘子Y，有最速上升算法的约束集为{Y}可以用来解决问题（6），其中被约束的最速上升方向是通过将D投影在凸的目标区域{Y}上而获得.结果表明在寻找被约束的最速上升方向的过程中可以得到原问题（4）的最优解.

1.3 MALM［15］

填充Toeplitz矩阵的MALM，其思想是在ALM算法的基础上，将迭代矩阵的对角元素均值化后重新赋值，使其保持Toeplitz结构.问题表述为

数值实验表明，与ALM和SVT算法相比，MALM算法的精度较高，收敛效果较好，对于在迭代过程中进行结构化处理的MALM算法保持了Toeplitz矩阵的结构，从而可以利用快速奇异值分解，使得在奇异值分解时间上要远短于其他2种算法；但是相比ALM算法，MALM算法在均值步增加了数据的传输.而对于一些计算机来讲，数据传输频繁会造成数据堆积而拖延计算时间，因此，基于减少数据传输量的思考，在迭代的尾端，即接近目标矩阵时再进行结构化处理是增效的选择.

1.4 l-TMALM

对矩阵利用ALM算法［11］的快速迭代l步之后，进行尾部修正及结构化处理.一方面，避免了均值步产生的频繁数据传输；另一方面，尾部修正使得迭代矩阵更加靠近目标矩阵，从而快速达到可行解，减少奇异值分解时间.算法步骤如下：

第1阶段：ALM算法步.

第1步：给定下标集合Ω，样本Toeplitz矩阵D，参数 ρ＞ 1，μ0＞ 0，以及初始矩阵 Y0，0=O，E0，0=O，k：=0，q=1，2，···，l-1.

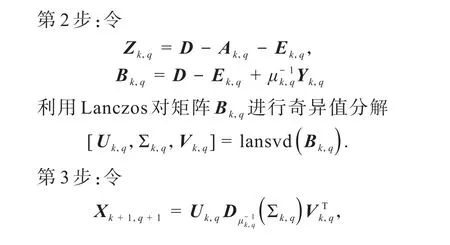
该算法分为2个阶段执行：第1阶段，使用ALM算法，利用ALM算法本身迭代速度快的性质，当其迭代到一定程度，即迭代矩阵逐渐靠近目标矩阵时；进入第2阶段，对迭代矩阵序列进行尾部修正并结构化，结构化使迭代矩阵与目标矩阵保持同样结构，从而可利用快速奇异值分解，修正使迭代矩阵从数值上更加逼近目标矩阵，以便快速地达到可行解.该算法不仅减少了频繁的数据传输量，而且在一定程度上节省了奇异值分解时间.

2 收敛性分析

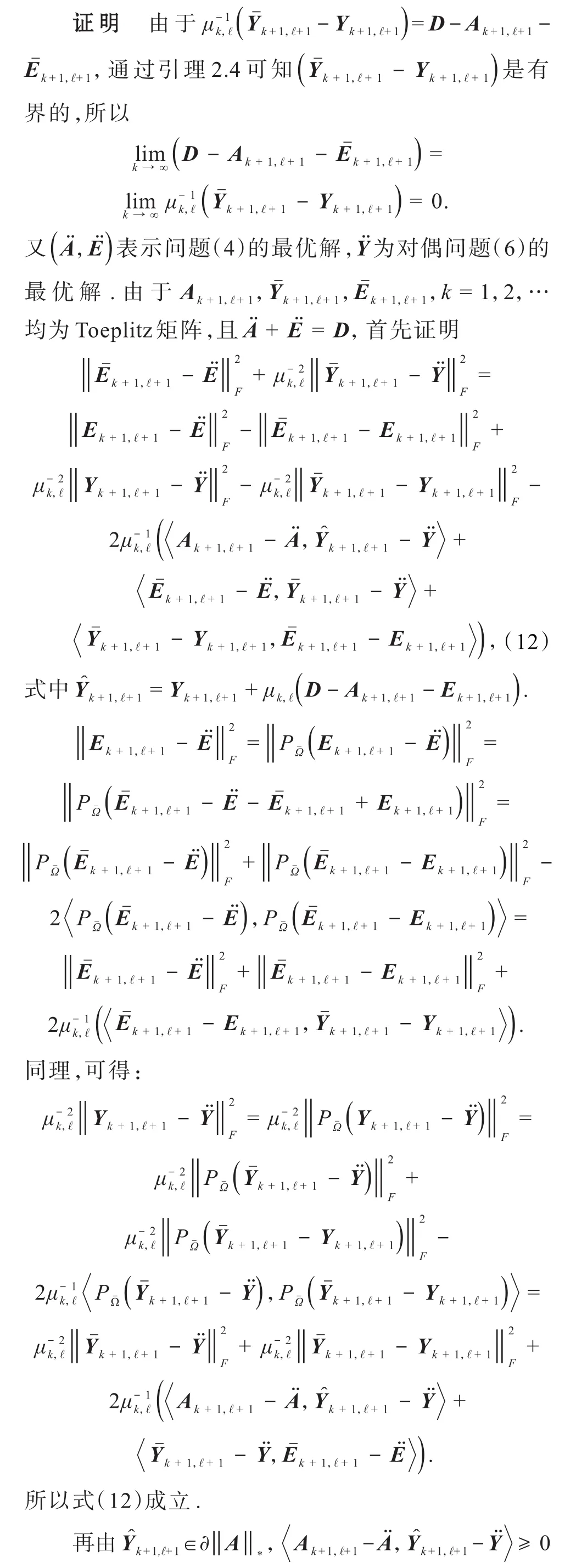
3 数值实验

通过数值实验比较了 l-TMALM、l-MALM［19］、MALM［15］以及 ALM 算法［11］，所有的数值实验均在相同工作环境中完成.实验中，通过对迭代步数（IT）、计算时间（time，单位为 s）、收敛误差 1和 2（E1，E2）的分析和比较，表明l-TMALM算法无论在迭代步数上还是在奇异值的分解时间上，明显优于其他3种算法.E1和E2的计算式分别为

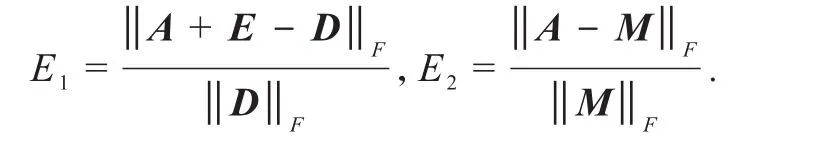
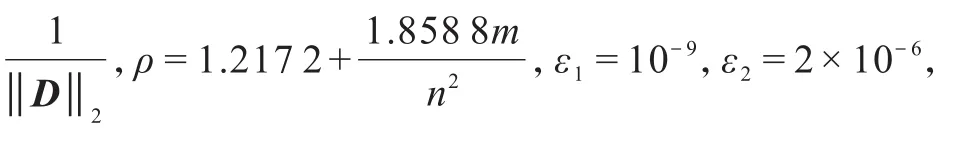
选取的样本矩阵阶数为m=n∈{800，1500，2 000，3000，4 000}，经过多次数据实验得出当第1阶段迭代步数l=6时，计算出的总迭代时间以及误差均可达到最小，所以第1阶段ALM算法步中的迭代步数l取值为6，采样率为p∈{0 .6，0.5，0.4} ，样本矩阵的秩为10.

4种算法的数值实验结果列于表1，4种算法均可成功地计算出满足规定停止准则的迭代矩阵.且l-TMALM算法在保证迭代步数和奇异值分解时间上均优于l-MALM，MALM以及ALM算法的情况下，其迭代矩阵与原始矩阵的逼近程度最好，即E2最小，收敛效果最好.同一采样率下，4种算法的时间比较如图1所示.表明同一矩阵阶数下，l-TMALM算法所用计算时间最短.

表1 不同采样率时4种算法比较

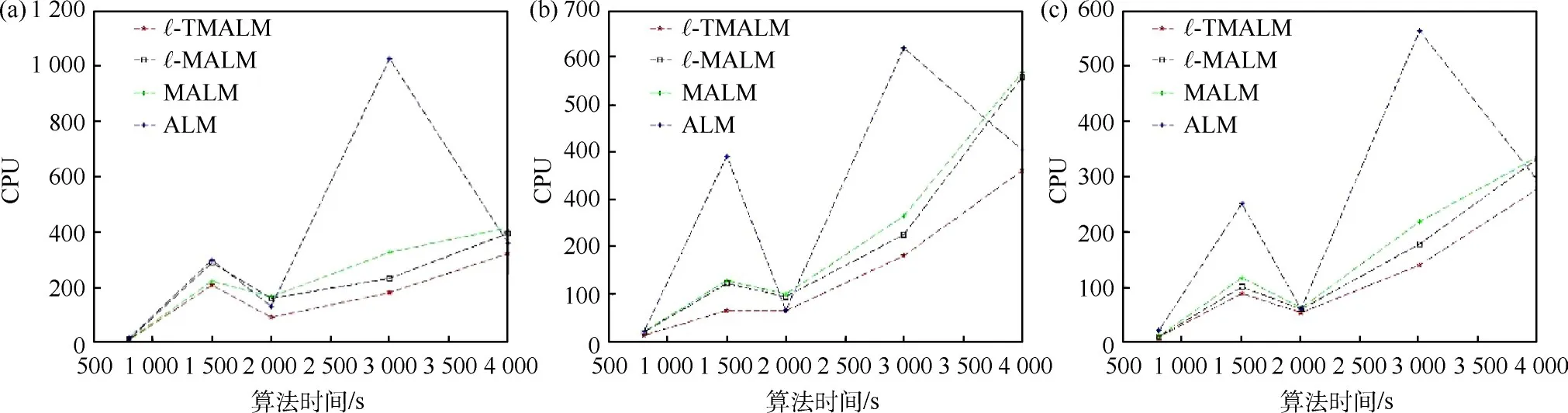
图1 不同采样率时4种算法时间比较（a）p=0.4；（b）p=0.5；（c）p=0.6

4 结束语

对于Toeplitz矩阵填充问题，本文基于MALM提出了一种l-TMALM算法.算法通过尾部修正再结构化，加速迭代矩阵与目标矩阵的逼近过程，以便快速地达到可行解，较大程度地缩短迭代步数；结构化使迭代矩阵与目标矩阵保持原有的Toeplitz结构，从而可利用快速奇异值分解缩短算法运行时间，降低计算代价.因此，新算法不仅克服了原始ALM算法较长的奇异值分解时间，也避免了MALM算法额外的数据传输量；此外，新算法的收敛效果要优于l-MALM，MALM以及ALM算法.基于新算法的合理性和有效性，建立了与之相对应的收敛性理论.理论分析和数值结果表明，l-TMALM算法是求解矩阵填充问题的一种有效算法.另外，未来拟将研究推广到高维的张量填充问题，比如将其修正的思想进一步推广到张量填充问题，从而求解出对于具有Toeplitz结构矩阵的张量填充算法.