冯志强，张鸿燕

（1.海南师范大学 数学与统计学院，海南 海口 571158；2.海南师范大学 信息科学技术学院，海南 海口 571158）

多元线性模型在科学、技术、经济、管理、军事等领域中有着广泛的应用，估计多元线性模型的参数是一个在理论上与实践上均有重大价值的实际问题。设X1,X2,…,Xn是n个自变量（解释变量），p1,p2,…,pn是模型参数，Y是因变量，则多元模型可以表示为

当d大于临界值dt时，认为点V对于该超平面即为外点（outliers）（见图1）。需要注意的是：dt通常是由实际的物理观测过程与问题的精度要求所决定的，某些情况下则难以明确dt的经验数值。

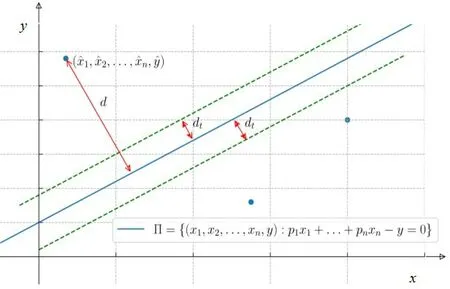
图1 外点示例Figure 1 Demonstration of outliers

各种最小二乘方法适用的前提是假定噪声服从正态分布（Gauss-Markov 假设）而且样本数据中不存在外点（outliers）。如果噪声不服从正态分布，采用以上方法估计会存在较大的误差；如果观测数据中存在外点，则参数估计的性能会很差甚至完全不能用。随机抽样一致性（RANdom SAmple Consensus，RANSAC）方法很好地解决了外点带来的问题[7-8]，它在外点的比例小于50%的条件下都可以使用。RANSAC方法是一种随机算法，在摄影测量与计算机视觉领域得到了广泛使用，但是在其他领域受关注的程度不高，而且这种迭代型的算法的时间复杂度比较高，不适合实时计算。

如果同时考虑噪声的统计分布偏离正态分布的情形以及存在外点的情形，线性模型参数估计的优化准则应当选择s= 1对应的l1范数作为误差的代价函数。采用l1范数最小化方法估计线性模型参数的难点在于代价函数不再是可微的，求解比较困难，但是估计的精度与稳健性很好。

在l1范数最小化的意义下估计线性模型（1）的参数向量p归结为求解超定线性方程组Ap=b，相应的最优化问题是

该问题的解称为方程组Ap=b在l1范数最小化意义下的解，简称为方程组的l1范数解。相应地，问题（P0）简称为l1范数最小化问题。

求解问题（P0）的方法已有不少，主要有线性规划方法[9]、投影下降法[10]、有效集法[11]、区间方法[12]等。这些方法各有优缺点，如线性规划方法使问题规模扩大，投影下降算法结构复杂性高，不易被工程技术人员掌握，有效集法算法简单直观，但是无法处理矩阵A行亏秩的情况，区间方法过于复杂并且无最优解区间的检验，比较麻烦。文献[13]针对问题（P0）提出了基于最小l1残差向量的数值解法，它将求解过程转化为一个约束不可微最优化问题的求解与相容线性方程组的求解。遗憾的是，该方法只适用于系数矩阵A是满秩的情况，即rank(A)=n。

本文进一步完善了文献[13]中的方法，得到基于基追踪与Moore-Penrose 广义逆的新型算法，该算法具有如下优点：增添了对系数矩阵A缺秩情况的处理，解除了对于满秩条件的限制；算法结构简单、易于操作、直观性强并且适合处理大规模问题。

为了后续讨论的方便，这里给出将会用到的一些数学记号及其解释（见表1）。

表1 部分数学符号说明Table1 Description of some mathematical notations

1 最小残差向量的性质及等价形式

最小l1残差向量的定义与性质如下[14]：

定义1（最小l1残差向量） 设popt为问题（P0）的解，称ropt=Apopt-b为问题（P0）的最小l1残差向量。如果能求得最小l1残差向量，那么相容线性方程组Ap=b+ropt的解即为问题（P0）的解。

定理1 设有两个超定线性方程组Ap=b与Bp=b，若存在可逆阵P使得B=Ap，则这两个超定线性方程组的最小l1残差向量相同。

引入最小l1残差向量的概念与基本性质的目的是确定超定线性方程的l1范数解的结构与表示，达成这个目标的关键是建立以下的定理。

于是定理2得证。

需要说明的是：为了提高本文提出的多元线性模型参数估计方法的适应性，本文对文献[13]给出的结果做了改进，即在式（9）与式（11）中用矩阵的Moore-Penrose伪逆A†1代替了文献[13]中所采用的矩阵逆A-11。

2 求解l1 范数最小化问题的稀疏优化方法

2.1 稀疏优化的等价转换

对于最小l1残差向量ropt，可以通过现有的优化方法求得它的一个稀疏解，即使得r中分量取0值的数目尽可能多。换句话说，求解问题（P1）就转换为l1范数最小化的稀疏优化问题，这可以通过基追踪方法来求解[15]。

2.2 算法描述

综合上述推导过程，可以得到问题（P0）的求解算法，相应的伪代码描述如算法1所示：

算法1：超定线性方程组最小l1 范数求解算法输入：A ∈Rm × n,b ∈Rm ×1,m ＞n ≥2输出：p ∈Rn ×1 1.初始化m为矩阵A的行数，n为矩阵A的列数；2.如果m ＜n输出错误信息：“矩阵A的行数必须大于列数”；3.取矩阵A的前n行构成矩阵A1：A1 ←A(1:n)；4.取矩阵A的n + 1～m行构成矩阵A2：A2 ←A(n + 1:m)；5.计算矩阵A1的Moore-Penrose逆：A†1 ←CalcMoorePenroseInverse（A1）；6.计算矩阵:C ←A2A†1；7.计算向量:w ←Cb(1:n) - b(n + 1:m)；8.设定矩阵:D ←[-C Im - n]；9.设定矩阵:Φ ←[D -D]；10.构建线性规划问题目标函数中的系数向量:c ←[1,1,...,1]T ∈R2m ×1；11.求解标准线性规划:αopt ←LinprogSolver(c,Aeq = Φ,beq = w,lb = 02m × 1)；12.求得最小模剩余向量:ropt ←αopt(1:m) - αopt(m + 1:2m)；13.计算矩阵A的Moore-Penrose逆：A† ←CalcMoorePenroseInverse（A）；14.计算最优参数向量：popt ←A†1(b + ropt)；15.返回popt，计算结束。

伪代码中的第11行用到了标准线性规划问题的求解器，第5行与第13行用到了Moore-Penrose 逆的求解器。前者有大量成熟的标准工具与软件包，后者也有备受欢迎的Greville列递推算法等多种方法[1，17]。

2.3 误差分析

若矩阵A行缺秩，由式（9）可知其并不影响算法对于问题（P0）的求解，故在这里只考虑矩阵A列缺秩的情况所带来的误差。

若矩阵A的列秩为rank(A)=k＞0，即列秩亏缺为n-k，则经过一定次数的初等变换后，可以得到如下关系：

3 验证与确认

3.1 满秩情况

问题：已知

构造约束最优化问题

即为超定线性方程组Ap=b的最小l1范数解。

3.2 列缺秩情况

在MATLAB 环境中分别构造线性模型的系数矩阵A∈Rm×n与向量u∈Rn×1，其中A、u中的每个元素均服从标准正态分布[18]。接着对A中的元素做出如下转换：

A(:,n-i) =A(:,1:k)fi,i= 0,1,…,n-k- 1， （30）

其中fi每次均随机产生，构造的矩阵A为列秩为k的矩阵（其中列缺秩为n-k）；最后令线性模型的右端向量b=Au，u即为符合式（24）的精确解。

令m= 10,n= 5，对列缺秩矩阵A构造的超定线性方程组进行求解（算法1）所得到的部分测试数据如表2所示。

表2 列缺秩矩阵A部分测试数据Table 2 Partial test data of column deficient rank matrix A

从数据中可以得到如下关系（考虑到计算机精度原因，其实际求解精度的数量级为10-15）：

将式（31）代入式（27）可知此时β= 0，且有

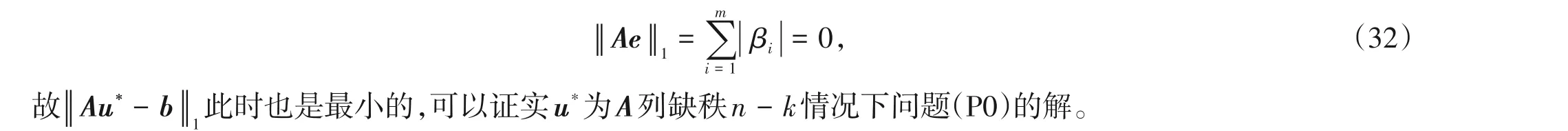
3.3 外点情况

不失方法上的一般性，取m= 100,n= 30，设定的理想参数向量p～1,p～2,p～3∈R30×1如表3所示：

表3 测试所用3种参数向量类型Table 3 Three types of parameter vector used in the test

在MATLAB 环境中构造系数矩阵A∈R100×30，其中n= 30,m= 100,A中的每个元素均服从标准正态分布[18]。距离临界值取为dt= 0.15。令bi=Ap～i,i= 1,2,3，在数据集Ω的y分量中添加强正态噪声ξ～N(0,5)使得点集合

如图2 所示，取ηoutlier=20%，对右端向量b中20%的元素进行扰动，图2 横坐标为数据点的分量序号i，纵坐标的值为右端向量b中yi分量的值(1 ≤i≤100)，添加强噪声扰动ξi后的分量坐标yi+ξi用虚线表示与加粗的点表示。

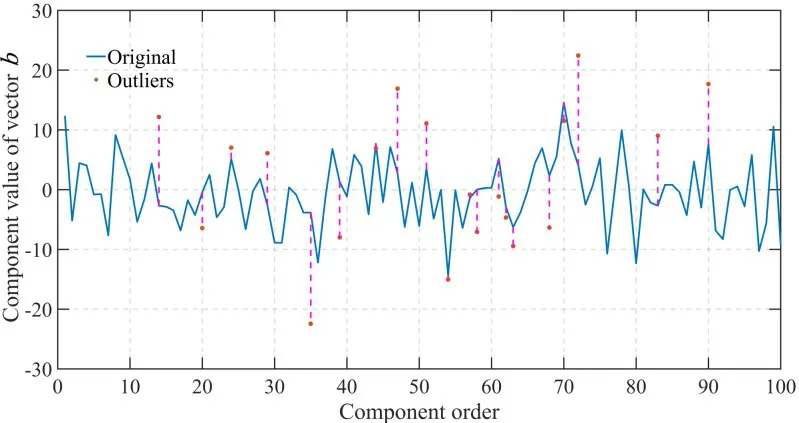
图2 在右端向量中添加强噪声使得数据点集Ω中20%的点成为外点Figure 2 Adding strong noise to the component y in b for the data set Ω such that the percentagte of outlers is 20%

本算例中，用于参数估计的点对是100个，25%比例的外点意味着有25个外点。从图3中误差曲线的趋势可以看出，算法是适用于各种数据类型的。从相对误差的数量级可以看出：最小l1范数解在外点比例不超过25%时具有非常好的稳健性，参数估计的相对误差的数量级控制在10-10以下，在外点比例接近27%～28%时，相对误差的数量级急剧增加到10-2；对于传统的最小二乘法，在只有一个外点的情况下其相对误差的数量级为10-1，此时参数估计的精度通常难以满足应用需求，随着外点比例的增加，相对误差接近于1，这意味着误差向量与精确解的二范数或能量基本相同，得出的参数估计值已经完全失效了。

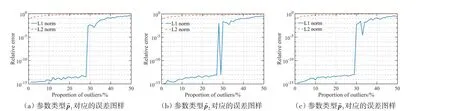
图3 不同参数类型下相对误差与外点比例的关系Figure 3 Dependence of relative error on proportion of outliers for different types of parameters

若定义图3中最小l1范数解的相对误差增加到10-3时对应的外点比例为临界误差外点比例，记为ηc，定义m n为数据的冗余程度，则在不同数据冗余度下的临界误差外点比例如图4所示：

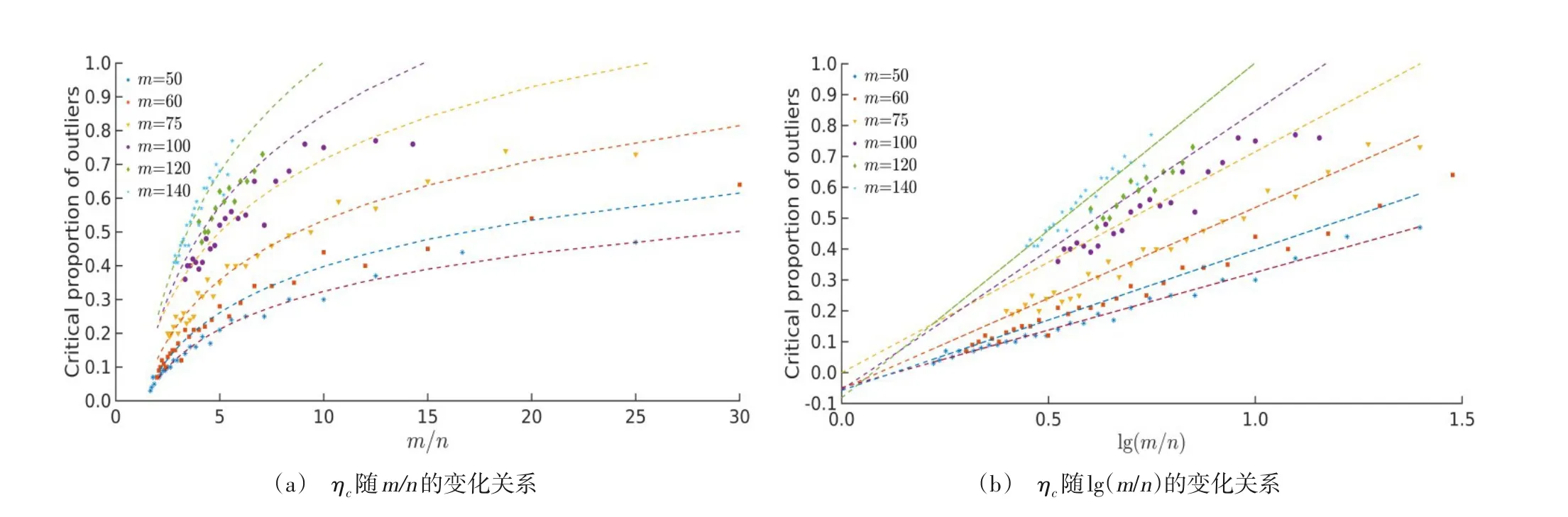
图4 临界误差外点比例与数据冗余度的关系0.5Figure 4 Dependence of critical proportion of outliers on data redundancy

从图4中可以看出：临界外点比例ηc与数据冗余度m n并非单纯的线性关系。随着数据冗余度m n的增大，临界外点比例ηc也对应增大（算法的性能更好）。尤其是当数据样本大于100（m＞100）时，较低的数据冗余度（m n＜5）也能使得算法求解的临界外点比例ηc＞50%，而基于最小二乘法的RANSAC方法对应的临界外点比例必须满足要求ηc＜50%。这表明基于l1范数的参数估计方法的稳健性优于RANSAC方法。

4 结论

本文利用残差向量l1范数最小化与基追踪准则给出了求解多元线性模型参数估计的最小l1范数解的一种稳健的新方法，通过相容线性方程组的引入极大地简化了原问题的求解步骤，并且针对参数矩阵A缺秩情况下算法的可行性进行了验证，证实了算法的有效性。数值仿真实验表明：在包含稀疏噪声的情况下，最小l1范数解优于最小二乘解；当噪声导致出现一定比例的外点时，最小二乘法则失效不能使用，但是本文提出的新方法在普遍的情形下当外点比例不超过25%时能有效地恢复真实的参数数值，而在数据冗余性比较高的场合，允许的临界外点比例超过50%。