赵丹丹，魏俊潮

(扬州大学 数学科学学院，江苏 扬州 225002)

本文中R表示一个有单位元的环.设*是环R到R的双射，若满足条件

(a*)*=a；(a+b)*=a*+b*；(ab)*=b*a*.

则称R为对合环，也简称为*-环[1].

设a∈R，若存在b∈R，满足

a=aba；b=bab；ab=ba.

则称a为R的群可逆元，且称b为a的群逆元.由文献[2]知，群可逆元的群逆元是唯一的.用a#表示群可逆元a的唯一的群逆元.用R#表示环R的全体群可逆元的集合.

设R是一个*-环，a∈R，若存在b∈R，满足

a=aba；b=bab；(ab)*=ab；(ba)*=ba.

则称a为R的Moore-Penrose可逆元，简称a为R的MP可逆元，且称b为a的MP逆元.由文献[3]知，a的MP逆元是唯一的，记为a+.用R+表示环R的全体MP可逆元的集合.

设R是一个*-环，a∈R，若aa*a=a，则称a为R的偏序等距元[4]，简称为PI元.用RPI表示环R的全体PI元的集合.当a∈R+时，a为R的偏序等距元当且仅当a+=a*.

设R是一个*-环，且a∈R#∩R+.如果a+=a#，则称a为EP元[5].用REP表示环R的全体EP元的集合.众所周知，a是EP元当且仅当a+a=aa+当且仅当a+a=a#a.

如果a+=a#=a*，则称a为强EP元[6]，简称SEP元.用RSEP表示环R的全体SEP元的集合.关于EP元、PI元及SEP元的刻画还可参见文献[7-9].

设R是一个*-环且a∈R，若a=a*，则称a是对称元；若aa*=a*a，则称a是正规元.关于正规元的研究可参见文献[10].

本文由既是群可逆元又是MP可逆元的元素a构造出一些MP可逆元及EP元，利用这些构造出的EP元和MP可逆元刻画元素EP性、PI性、SEP性及正规性等，并借助于一些已知的公式，构造出一个方程，研究这个方程在给定集合中有解时来刻画PI性质.最后一般化构造的方程并讨论一般化后的方程的一般解，变形一般解刻画EP性及PI性.这是研究广义逆的新方法.

引理1设a∈R#∩R+，则a#a*∈REP且(a#a*)+=(a+)*a2a+.

证明由于

(a#a*)((a+)*a2a+)=a#(a*(a+)*)a2a+=(a#a+a)a2a+=a#a2a+=aa+；

((a+)*a2a+)(a#a*)=(a+)*(a2a+a#)a*=(a+)*aa#a*=((a+)*a+a)aa#a*

=(a+)*(a+a2a#)a*=(a+)*a+aa*=(a+)*a*=aa+；

(a#a*)((a+)*a2a+)(a#a*)=((a#a*)((a+)*a2a+))(a#a*)=aa+a#a*=a#a*；

((a+)*a2a+)(a#a*)((a+)*a2a+)=((a+)*a2a+)((a#a*)((a+)*a2a+))

=(a+)*a2a+aa+=(a+)*a2a+；

因此a#a*∈REP且(a#a*)+=(a+)*a2a+.

由引理1的证明可得下列推论.

推论1设a∈R#∩R+，则

(1)a#a+a3=a=a3a+a#；

(2) (a+)*aa#=(a+)*=a#a(a+)*.

命题1设a∈R#∩R+，则a#a*a∈R+且(a#a*a)+=a+(a+)*a2a+.

证明由引理1可得

(a#a*a)(a+(a+)*a2a+)=(a#a*aa+)((a+)*a2a+)=(a#a*)((a+)*a2a+)=aa+；

(a+(a+)*a2a+)(a#a*a)=a+(((a+)*a2a+)(a#a*))a=a+aa+a=a+a；

故a#a*a∈R+且(a#a*a)+=a+(a+)*a2a+.

推论2设a∈R#∩R+，则a∈REP当且仅当a#a*a∈REP.

证明“⟹”由于a∈REP，故aa+=a+a.因此由命题1的证明知

(a#a*a)(a+(a+)*a2a+)=(a+(a+)*a2a+)(a#a*a).

于是a#a*a∈REP.

“⟸”假设a#a*a∈REP，则(a#a*a)(a#a*a)+=(a#a*a)+a#a*a.故由命题1的证明知，aa+=a+a.

从而有a∈REP.

定理1设a∈R#∩R+，则

(1)a∈REP当且仅当(a#a*a)+=a+(a+)*a；

(2)a∈RPI当且仅当(a#a*a)+=a+a3a+；

(3)a∈RSEP当且仅当(a#a*a)+=a；

(4)a是正规元当且仅当(a#a*a)+=(a+)*；

(5)a是2-正规元当且仅当(a#a*a)+=a(a+)*a+；

(6)a是对称元当且仅当(a#a*a)+=a#.

证明(1) “⟹”由于a∈REP，故a+=a#.从而由命题1知

(a#a*a)+=a+(a+)*a2a+=a+(a+)*a.

“⟸”若(a#a*a)+=a+(a+)*a，则由命题1知，a+(a+)*a2a+=a+(a+)*a.左乘aa*a得a3a+=a2，故a∈REP.

(2) “⟹”由于a∈RPI，故(a+)*=a.由命题1知(a#a*a)+=a+(a+)*a2a+=a+a3a+.

“⟸”若(a#a*a)+=a+a3a+，则由命题1知a+(a+)*a2a+=a+a3a+.右乘a#，利用推论1得a+(a+)*=a+a.再左乘a得(a+)*=a.从而a∈RPI.

(3) “⟹”由于a∈RSEP，故a∈RPI且a+=a#.由(2)知(a#a*a)+=a+a3a+=a#a3a#=a.

“⟸”若(a#a*a)+=a，则由命题1知a+(a+)*a2a+=a.右乘a#得a+(a+)*=aa#，故

aa+(a+)*=aaa#，即(a+)*=a，从而a∈RPI.此时有aa#=a+(a+)*=a+a，故a∈REP，因此a∈RSEP.

(4) “⟹”由于a是正规元，故a为EP元，且a#a*=a*a#，所以a(a#)*=(a#)*a.由命题1知

(a#a*a)+=a+(a+)*a2a+=a+(a#)*a2a#=a+(a#)*a=a+a(a#)*=(a#)*=(a+)*.

“⟸”若(a#a*a)+=(a+)*，则a#a*a=a*.右乘a+a得a*=a*a+a，因此a=a+a2，即a∈REP.

故aa*=aa#a*a=a#aa*a=a+aa*a=a*a.所以a是正规元.

(5) “⟹”由于a是2-正规元，则a是EP元且a2a*=a*a2，故a*a*a=aa*a*.

于是a*a*a#=a#a*a*，进而有a*a*a+=a+a*a*，从而(a+)*a2=a2(a+)*.由命题1知

(a#a*a)+=a+(a+)*a2a+=a+a2(a+)*a+=a(a+)*a+.

“⟸”若(a#a*a)+=a(a+)*a+，则由命题1知a+(a+)*a2a+=a(a+)*a+.右乘a得

a+(a+)*a2=a(a+)*.左乘1-a+a得(1-a+a)a(a+)*=0.右乘a*a#a得(1-a+a)a=0，从而a是EP元.故a2(a+)*=a(a+(a+)*a2)=(a+)*a2，即有a+(a*)2=(a*)2a+，从而a#(a*)2=(a*)2a#.进一步有a(a*)2=(a*)2a，所以a是2-正规元.

(6) “⟹”由于a是对称元，则a*=a且a是EP元.由1)知

(a#a*a)+=a+(a+)*a=a+(a+)*a*=a+=a#.

“⟸”若(a#a*a)+=a#，则由命题1知，a+(a+)*a2a+=a#.先右乘a#，由推论1得a+(a+)*=a#a#.再左乘a得(a+)*=a#.从而有a#=a+(a+)*a2a+=a+a#a2a+=a+.注意到a=aa*(a+)*=aa*a#，所以a+a=a+aa*(a+)*=a+aa*a#=a*a#.于是a=a#a2=a+a2=a*a#a=a*aa+=a*，故a是对称元.

命题2设a∈R#∩R+，则a+a3a+∈R+且(a+a3a+)+=a#.

证明注意到a#=a#a*(a+)*，a+a3a+=a*(a+)*a2a+，由引理1知

(a+a3a+)a#=a*(((a+)*a2a+)(a#a*))(a+)*=a*aa+(a+)*=a+a；

a#(a+a3a+)=(a#a*(a+)*a*)((a+)*a2a+)=(a#a*)((a+)*a2a+)=aa+.

因此a+a3a+∈R+且(a+a3a+)+=a#.

命题3设a∈R#∩R+，则a*a#a*∈R+且(a*a#a*)+=(a+)*a(a+)*.

证明注意到(a+)*a(a+)*=(a+)*a2a+(a+)*，由引理1知

(a*a#a*)((a+)*a(a+)*)=a*(a#a*)((a+)*a2a+)(a+)*=a*aa+(a+)*=a+a；

((a+)*a(a+)*)(a*a#a*)=(a+)*a2(a+(a+)*a*)(a#a*)=((a+)*a2a+)(a#a*)=aa+.

故a*a#a*∈R+且(a*a#a*)+=(a+)*a(a+)*.

由命题2及命题3有下面的推论.

推论3设a∈R#∩R+，则下列条件等价.

(1)a∈REP；

(2)a+a3a+∈REP；

(3)a*a#a*∈REP.

由于当a∈R#∩R+时，(a+)*a2=(a+)*a2a+a，而且

(a+a#a*)((a+)*a2)=a+((a#a*)(a+)*a2a+)a=a+aa+a=a+a；

((a+)*a2)(a+a#a*)=(a+)*aa#a*=(a+)*a*=aa+.

从而有下面的命题:

命题4设a∈R#∩R+，则

(1)a+a#a*∈R+且(a+a#a*)+=(a+)*a2；

(2)a∈REP当且仅当a+a#a*∈REP.

命题5设a∈R#∩R+，则a+a#a*a∈REP且(a+a#a*a)+=a+(a+)*a2.

证明利用命题4常规验证即可.

当a∈RPI时，(a+)*=a，由命题5知，一方面有

(a+a#a*a)+=a+a3=a+a(a+)*(a+)*；

另一方面又有

(a+a#a*a)+=a+a3=a+a2(a+)*.

故可构造方程

a+ax(a+)*=a+a2x.

(1)

命题6设a∈R#∩R+，则a∈RPI当且仅当方程(1)在χa中至少有一个解.

证明“⟹”当a∈RPI时，x=(a+)*为方程的一个解.

“⟸”(1)若x=a为解，则a+a2(a+)*=a+a3.左乘a#，由推论1得(a+)*=a，故a∈RPI.

(2)若x=a#为解，则a+aa#(a+)*=a+a2a#，由推论1知a+(a+)*=a+a.左乘a得(a+)*=a，故

a∈RPI.

(3)若x=a+为解，则a+aa+(a+)*=a+a2a+，即a+(a+)*=a+a2a+.先左乘a得(a+)*=a2a+.再右乘aa#得(a+)*=a.故a∈RPI.

(4)若x=a*为解，则a+aa*(a+)*=a+a2a*，即a+a=a+a2a*.左乘a得a=a2a*.由文献[4]知

a∈RPI.

(5)若x=(a#)*为解，则a+a(a#)*(a+)*=a+a2(a#)*，即(a#)*(a+)*=a+a2(a#)*.先右乘

1-a+a得a+a2(a#)*(1-a+a)=0.然后左乘a+a#a得(a#)*(1-a+a)=0.再左乘a+a*，由推论1得

a+(1-a+a)=0.从而a∈REP，而且(a#)*(a+)*=a+a2(a#)*=a(a#)*，此时a+a#=a#a*.最后左乘

a3得a=a2a*，故a∈RPI.

(6)若x=(a+)*为解，则a+a(a+)*(a+)*=a+a2(a+)*.先左乘a，然后右乘a*，得

a(a+)*aa+=a3a+.再右乘aa#，利用推论1得a(a+)*=a2.最后左乘a#得(a+)*=a，故a∈RPI.

方程(1)可一般化为

a+ax(a+)*-a+a2y=0.

(2)

命题7设a∈R#∩R+，则方程(2)的一般解为

(3)

证明首先证明公式(3)是方程(2)的解.事实上

a+a(-a+apa*+u-a+auaa+)(a+)*-a+a2(-a#pa+a+z-a#az)

=-a+apa*(a+)*+a+au(a+)*-a+auaa+(a+)*+a+a2a#pa+a-a+a2z+a+a2a#az

=-a+apa+a+a+au(a+)*-a+au(a+)*+a+apa+a-a+a2z+a+a2z=0.

故公式(3)是方程(2)的解.

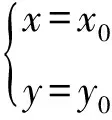
-a+a(-ay0)a*=(a+a2y0)a*=a+ax0(a+)*a*=a+ax0aa+，

于是x0=-a+a(-ay0)a*+x0-a+ax0aa+.又因为

-a#(-ay0)a+a=(a#a+a)ay0a+a=a#(a+a2y0)a+a=a#(a+ax0(a+)*)a+a

=(a#a+ax0)((a+)*a+a)=a#(a+ax0(a+)*)=a#(a+a2y0)=a#ay0.

故y0=-a#(-ay0)a+a+y0-a#ay0.于是方程(2)的一般解为公式(3).

推论4设a∈R#∩R+，则a∈RPI当且仅当方程(2)的一般解为

(4)

证明“⟹”由于(2)的一般解由(3)式给出，故a∈RPI时，(3)式即为(4)式，从而(2)的一般解由(4)式给出.

“⟸”若方程(2)的一般解由(4)式给出，则

a+a(-a*apa*+u-a+auaa+)(a+)*-a+a2(-a#pa+a+z-a#az)=0，

即对任意p∈R，有-a*apa+a+a+apa+a=0.特别地, 选取p=a，则有a*a2=a+a2，因此a∈RPI.

方程(2)可改为如下方程

a#ax(a+)*-a+a2y=0.

(5)

推论5设a∈R#∩R+，则a∈REP当且仅当方程(5)的一般解由(3)式给出.

证明“⟹”假设a∈REP，则a+a=a#a.此时方程(5)即为方程(2)，从而方程(5)的一般解由(3)式给出.

“⟸”若方程(5)的一般解由(3)式给出，则

a#a(-a+apa*+u-a+auaa+)(a+)*-a+a2(-a#pa+a+z-a#az)=0，

即对任意p∈R，有a#apa+a=a+apa+a.取p=1，有a#a=a+a，故a∈REP.