孙丰霖

(中国海洋大学海洋与大气学院，山东青岛 266100)

1 引言

在谱分析中，凝聚谱(MSC)是衡量两个序列在频域上相关性的重要工具，有十分广泛的应用[1-4]。在实际应用中，常常采用Welch方法对MSC进行估计[1-4]，通过加窗和重叠分段两种方式来降低估计的偏差与方差，从而提高MSC估计量的准确度[1-5]。

估计量的偏差和方差是衡量一种估计方法优劣的两个重要方面，因此了解Welch方法得到的MSC估计量的偏差与方差是十分必要的。非重叠情形下，MSC估计量的偏差与方差可以直接通过分布函数获得[3]，然而，重叠情形下MSC分布尚未导出，致使MSC偏差与方差无法计算。

一些国外学者针对重叠情形下的MSC估计量的分布进行了研究。例如Bortel和Sovka[4]给出了75%重叠率下MSC估计量的渐进分布，该方法以非重叠情形下的MSC估计量的分布函数为基础，对其中的自由度参数进行修正，并给出适用范围，然而文章并没有涉及实际中常用的50%重叠率。Gallet和Julien[2]针对50%和75%重叠率下，对MSC的显著性阈值进行讨论，针对MSC总体值γ2为0的情形，对MSC估计量的分布进行讨论，从而得出阈值的适用范围，不过文章没有涉及γ2不为0的情形。

国内学者对Welch方法估计量的偏差与方差的讨论大多集中在功率谱方面，包括窗函数、重叠率和分段数等因素的影响[5-10]，而对通过Welch方法估计MSC研究较少，因此本文基于这一现状，对Welch方法下MSC估计量的偏差与方差进行研究，给出四种估计偏差和方差的方法，并通过随机模拟，基于估计值和实际值之间的相对误差，对四种方法进行比较并给出各个方法的适用范围，最后对结论的稳定性进行分析。

2 Welch方法

假设x(t)和y(t)为两个总长度为N的离散时间序列，分别进行可重叠的分段，即

xi(t)=x((i-1)D+t)

yi(t)=y((i-1)D+t)

(1)

其中i=1，2，…，Ns，t=1，2，…，L，Ns为总分段数，L为段长，D分段间的延迟量，则重叠率为p=100(1-D/L)%，通过式(2)估计MSC。

(2)

其中F为Fourier变换，*为复共轭，w(t)为数据窗。在非重叠情形下，MSC的分布已经由Carter 等[3]证得，此时MSC的偏差(记为Bias)与方差(记为Var)如下：

(3)

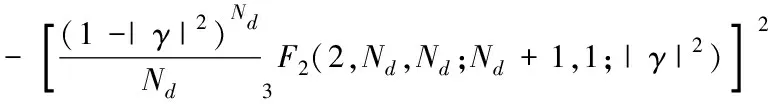
(4)

其中Nd是非重叠情形下的分段数

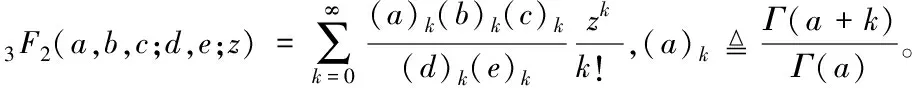
Nd=(Ns-1)(1-p)+1

(5)

若将式(3)和式(4)中的Nd替换为Ns来估计MSC的偏差与方差，这实际上默认了重叠并不会对MSC的分布产生影响，但事实上，重叠的做法让部分数据多次使用，让相邻分段相关性增强。Gallet和Julien[2]针对MSC显著性检验问题，给出了两种修正Ns的方法。第一种方法(式(6))基于修正功率谱自由度的思想，即将窗函数和重叠率的影响考虑进来。

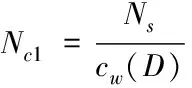
(6)

(7)

(8)

第二种方法是基于参数估计的思想，当γ2为0时，在非重叠情形下有E2=1/Nd，因此，若假定重叠前后MSC估计量分布未发生较大变化，则可以用Nc2(式(9))作为Nd的修正。

(9)

然而，这两种修正方法仅讨论当γ2为0时，修正后的MSC分布函数是否与随机模拟得到的累积经验分布函数(基于两个独立白噪声序列计算得到)的一致。在本文，探究这两种修正方法是否能应用于γ2≥0时的偏差与方差估计。

3 随机模拟

采用随机模拟生成不同MSC真实值γ2、分段数Ns和重叠率p下的MSC样本，随机模拟的参数见表1，模拟序列生成方法参考Carter等[3]，采用Hanning数据窗[2]，重复m=1×105次实验，得到MSC估计量的偏差B(式(10))与方差V(式(11))的实际值，作为真实值的代表。

表1 随机模拟参数

(10)

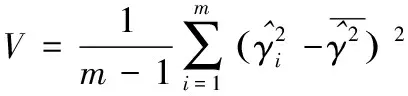
(11)

首先，探究分段数和重叠率对MSC估计量实际偏差与方差的影响。从图1a可见，偏差会随着γ2的增大而逐渐减小直至0(当γ2=1时)。当分段数Ns=5时，25%和50%重叠率下的偏差曲线比较接近，而75%重叠率下的偏差明显增大，当提高分段数至15和30时，偏差出现明显的减小。从图1b可见，方差随着γ2的增大出现先上升后下降的趋势，并在γ2=1/3时达到最大值。当分段数Ns=5时，25%和50%重叠率下的实际方差曲线比较接近，而75%重叠率下的方差明显增大，当提高分段数至15和30时，方差曲线出现明显的降低，这与非重叠情形下的结论相吻合[3]。因此，重叠情形下，随着分段数的增加，偏差和方差明显降低。

图1 重叠率和分段数对MSC估计量偏差和方差的影响

从图1可见，在给定分段数Ns=5情形下，25%和50%重叠率的偏差和方差曲线十分接近，不过25%重叠率所使用的数据是50%情形下的1.33倍，数据量提升了约33%，但方差和偏差却没有得到相应程度的减小。虽然75%重叠率进一步利用了有限的数据，但这导致了MSC的分布出现较大变化，使得MSC估计量的统计性质由非重叠下情形向75%重叠率推广的过程中产生一定问题，这已经在75%重叠率阈值的适用范围的结论中得到了验证[2]。

因此，在实际应用中，50%成为估计MSC常用的重叠率，原因包括，一是在有限的数据量下能够让MSC估计量的偏差和方差有效降低，二是计算简单，MSC估计量的统计分布变化小，可利用非重叠情形下的结论进行扩展。

下面，在不同重叠率下，比较四种计算偏差和方差的方法的估计效果。将Nd、Ns、Nc1和Nc2分别代入式(3)，计算偏差估计值，分别记为Bd、Bs、Bc1和Bc2，代入式(4)，计算方差估计值，分别记为Vd、Vs、Vc1和Vc2，以Ns=5情形为例，绘制偏差和方差估计值曲线(图2)。

对偏差而言，在25%重叠率下，除Bd外，其它三条估计曲线与实际值曲线B十分接近，但随着重叠率提高到50%，Bs出现一定程度的偏离，Bc1和Bc2接近实际值曲线B，当重叠率上升到75%，Bs的偏离程度更加明显，同时Bc1也位于实际值曲线B下方，只有Bc2仍然接近实际值曲线。

对方差而言，结论与偏差相似。在25%重叠率下，Vs、Vc1和Vc2与实际值曲线非常吻合，50%的重叠率令Vs开始出现细微的偏离，Vc1和Vc2与实际值吻合度较好，然而75%重叠率下，Vd高估了方差，而Vs和Vc1估计值偏低，Vc2也在γ2<1/3时高估了实际方差，不过这种影响在γ2>1/3后逐渐减弱消失。

图2 偏差和方差的估计效果

从图2可见，重叠情形下，由于Bd和Vd与真实值之间差距过大，因此使用Nd来估计偏差与方差是不合适的，这个结论在其它Ns同样成立，因此在接下来评价估计效果时，不再对Nd进行讨论。

下面，针对不同的分段数，对Ns、Nc1和Nc2估计偏差和方差的整体效果进行讨论。对方法Ns，定义偏差和方差的相对误差为

(12)

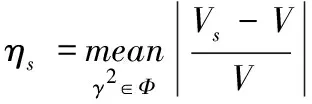
(13)

其中Φ为随机模拟中γ2的取值集合，mean为取平均，同理，Nc1和Nc2偏差和方差的相对误差记为ζc1，ζc2，ηc1和ηc2。ζ和η能衡量在整个γ2的取值范围内，估计方法得到的偏差和方差估计值与实际值之间的整体差距。三种估计方法的相对误差结果见表2，选择5%作为判断该方法是否适用的阈值，即如果某估计方法在重叠率p和分段数Ns下的相对误差小于5%，则认为该方法可以用来估计偏差和方差。选择5%作为阈值的理由在于，Gallet和Julien[2]利用KS检验对γ2=0情形下对MSC估计量的分布进行了讨论，并利用式(6)和式(9)对非重叠情形下的分布函数进行修正，给出50%和75%重叠率下修正后分布函数的适用范围。在这些适用范围中，当γ2=0时，本文计算的偏差与方差的相对误差均处于5%以内，因此将5%作为衡量估计值与实际值之间是否吻合的阈值。

表2 偏差估计值与实际值之间相对误差ζ/%

表3 方差估计值与实际值之间相对误差η/%

从表2可见，在25%重叠率下，Ns、Nc1和Nc2三种修正方法得到的偏差估计值均能使相对误差控制在5%以内，在50%重叠率下，从Ns>9开始，ζs出现一定程度的增长，超过了5%的阈值范围，且随Ns增大没有表现出明显规律，说明50%重叠率下使用Ns估计偏差的效果不够稳定。ζc1和ζc2依然能够控制在5%以内。在75%重叠率下，ζs在所有Ns下均超过了34%，且随Ns增大呈现一定上升趋势。在Ns<11时的ζc1超过了5%，在Ns≥11时的ζc1小于5%，而Nc2始终能够控制ζc2在5%以内。

从表3可见，在25%重叠率下，Ns、Nc1和Nc2三种修正方法得到的方差估计值均能使相对误差控制在0.6%以内，在50%重叠率下，从Ns≥15开始，ηs出现一定程度的增长，超过了5%的阈值范围，且随Ns增大呈现一定程度的上升，说明50%重叠率下使用Ns计算方差效果不够稳定。ηc1和ηc2能够控制在1.2%以内。在75%重叠率下，ηs在所有Ns下均超过了15%，且随Ns增大呈现一定上升趋势。在Ns<9时的ηc1超过了5%，在Ns≥9时ηc1控制在5%以内，且随着Ns增大呈现一定程度的下降，Nc2在Ns≥5能够将ηc2控制在5%以内，也随着Ns增大逐渐减小。

表4 不同重叠率下各方法适用范围

结合表2和表3结果，给出不同重叠率和分段数下，给出三种方法估计MSC的适用范围(表4)。在25%重叠率下，三种方法计算的偏差和方差均与实际值比较吻合，其中直接使用Ns计算是比较准确和快速的方法。在50%重叠率下，Nc1和Nc2计算偏差和方差相对准确，Nc1只需根据重叠率和数据窗进行计算，而Nc2需通过随机模拟生成MSC样本估计，因此前者是50%重叠率时计算偏差与方差比较好的选择。在75%重叠率下，Nc1的适用范围小于Nc2的适用范围，即使在Ns≥11时，使用Nc1计算的偏差与方差的相对误差高于Nc2，不过差距随着Ns增大而逐渐减小。

4 稳定性分析

在第3节中，生成给定γ2的两个时间序列是基于服从N(0，1)白噪声序列(以下称为“基序列”)，下面将基序列分布进行修改，首先提高方差，变为服从N(0，9)的白噪声序列，其次，弱化不同时间点间相互独立的假设，变为参数为0.5的AR(1)序列，重复偏差和方差实际值的计算过程，验证本文结论的稳定性。

当基序列变为N(0，9)的白噪声序列(或AR(1))时，计算此时的实际偏差与方差和N(0，1) 情况下实际偏差与方差的相对误差

(14)

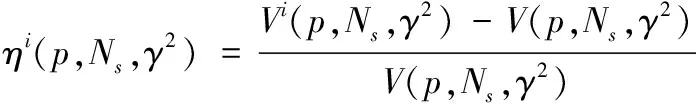
(15)

其中，i=1代表N(0，9)，i=2代表AR(1)，绘制ζi和ηi的分布直方图(图3)。当模拟基序列改为N(0，9)时，MSC偏差的实际值变化幅度处于[-13%，13%]，约92%的相对误差集中在[-5%，5%]，而方差实际值变化幅度处于[-2.75%，2.75%]，约93%的相对误差集中在[-1.25%，1.25%]。当模拟基序列改为AR(1)时，偏差与方差实际值的相对误差分布状况与N(0，9)情形下的结果十分相似，约91%的偏差相对误差集中在[-5%，5%]，约94%的方差相对误差集中在[-1.25%，1.25%]，使用KS test检验图3a、图3b中样本是否来自同一分布，p值分别为0.86和0.98，不拒绝来自同一分布的假设。

图3 稳定性分析

综上，随机模拟中基序列改变并不会对偏差和方差的实际值产生较大影响，同时，Ns、Nc1和Nc2三种方法的适用范围(表4)并未随着基序列改变发生变化，因此，本文给出的Ns、Nc1和Nc2三种方法的适用范围具有一定的稳定性。

5 结论

本文研究了基于Welch方法，不同重叠率下MSC估计量偏差和方差的估计问题，给出四种估计偏差和方差方法，并通过随机模拟对这四种方法的估计效果进行比较，给出各个方法的适用范围，并通过改变随机模拟基序列的方式验证本文结论的稳定性。主要结论包括：

1)在25%重叠率下，使用Ns、Nc1和Nc2三种方法得到的偏差与方差估计值与实际值比较吻合。由于Ns不需通过计算即可得到，是一种比较合适的估计方法。

2)在50%重叠率下，使用Nc1和Nc2得到的偏差与方差与实际值均比较吻合。前者计算需要窗函数和重叠率，后者需要随机模拟样本对参数进行估计，同时需要足够样本量保证参数的稳定性，因此前者是相对比较合适的方法。

3)在75%重叠率下，Nc1的适用范围需要保证Ns≥11，而Nc2的适用范围需要保证Ns≥5，且后者的相对误差要优于前者，不过这种差距随着Ns的增大逐步减小。