Tao Li(李涛) Lin Yan(严霖) and Zhigang Zheng(郑志刚)

1College of Information Science and Technology,Huaqiao University,Xiamen 361021,China

2Institute of Systems Science,Huaqiao University,Xiamen 361021,China

3School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China

Keywords: self-sustained oscillation,excitable network,functional-weight approach

1. Introduction

In recent years, the study of dynamics on complex networks has attracted great attention due to its extensive practical applications in a number of fields ranging from physics,chemistry, biology, and even social science.[1-8]Much effort has been devoted to studies of synchronization,[9-12]spreading and wave propagation dynamics.[13-17]It has been revealed that the topology of networks plays an important role in dominating the synchronizability and the spreading efficiency on networks. Moreover, it has been revealed that there exist close relations between synchronization and propagation dynamics,[18]implying the inherent and universal mechanism in various seemingly different dynamical behaviors. It is significant to unravel these essential ingredients embedded in spatiotemporal dynamics.

Self-sustained oscillation is a typical solution of many nonlinear dynamical systems. For a non-oscillatory system,oscillatory motion can be induced and maintained by external drives. The essential mechanism of sustained oscillation is the nonlinearity-induced competition and balance between the internal instability and the nonlinear feedback.[19]On the other hand,the emergence of sustained oscillations of a network of coupled non-oscillatory elements is obviously a highly nontrivial collective behavior, which strongly relies on the collaboration of these elements. Because each unit in the system does not exhibit oscillatory behavior,the feedback mechanism of sustained oscillations should be due to the collaborative feedback of units. For example, it has been found that as many excitable nodes are organized as a network,sustained oscillation can be found through a collaboration of these excitable elements.[20-22]Periodic and even chaotic oscillations in gene-regulated networks have also been observed as a prototype of biological clocks.[23]Explorations of these emergent oscillatory behaviors are potentially important because a number of phenomena such as memory formation in neuron and brain dynamics,[24,25]cardiac dynamics,[26,27]and biological rhythms are closely related to this collective behavior.

For a given network composed of a large number of nonoscillatory nodes, only a portion of elements will participate in the formation of the sustained oscillation. It is thus very interesting and important to explore the mechanism of oscillatory dynamics when these units interact with each other and study how a number of non-oscillatory nodes organize themselves to emerge a collective oscillatory phenomenon. It has been revealed that for an excitable network,oscillatory motion is usually contributed by a small portion of units that serves as the oscillation source, and other elements act as the propagation path of this oscillation. An important topic in revealing the coordinated dynamics of non-oscillatory units is to explore the core structure that is responsible for the persistence of oscillation and the propagation paths of the oscillation in the network. Very early studies revealed that the loop topology,which was later called the Winfree loop,[28]is the key source that produces the persistent oscillatory motion. This type of loop topology was recently clearly studied in terms of the socalled dominant-phase advanced driving(DPAD)method.[29]The merit of the DPAD method is that it is convenient to compare the phase relations among different units in a network as long as a normal oscillation and moreover a well-behaved phase can be defined. This means that this approach will be unavailable if the oscillation behavior is so complicated or even non-stationary that an appropriate phase cannot be introduced.

Apart from this approach,the functional-weight approach was proposed in searching the fundamental building blocks in the collective oscillation in gene-regulated networks, and various different basic motifs have been found by using this method. On the gene-regulated network, the behavior of one gene is usually described by the one-dimensional dynamics. It is interesting to apply the functional-weight method to study the oscillation in networks of non-oscillatory units with higher-dimensional dynamics.

In this paper,we develop the functional-weight approach that has been successfully used in studies of sustained oscillations in gene-regulated networks by an extension to the highdimensional node dynamics. This approach can be well applied to the study of sustained oscillations in coupled excitable units. We tested this scheme for different networks, such as homogeneous random networks, small-world networks, and scale-free networks and found it can accurately dig out the oscillation source and the propagation path. The present approach is believed to have the potential in studies competitive non-stationary dynamics.

2. Improved functional–weight method

The functional-weight scheme was first proposed by Zhanget al.and was successfully applied to explore the topology dependence of the oscillatory dynamics on large-scale gene-regulatory networks (GRN).[30,31]The main ingredient of the functional-weight approach is to quantitatively evaluate the significance of various interactions(links),further keep those connections with higher weights. By applying the FW approach, the relative weight of each interaction edge can be quantitatively calculated from the dynamical data of the oscillatory networks by applying this approach, which eventually identifies a small portion of key nodes and connections with larger weight as the oscillation source and paths,which eventually leads to a simplified directed network in revealing the essence of dynamical processes on networks. This is an important operation of network reduction through the evaluation of dynamical influences.

It is promising to be applicable to studies of the collective oscillatory motion in networks of excitable nodes. However,the original functional-weight method was only used for the case of one-dimensional node dynamics,where a definite fixed point exists. For most of excitable node dynamics, at least one excitation variable and one recovery variable are necessary,i.e., the node dynamics of an excitable node should be described in terms of two-dimensional phase space. Therefore we propose the improved functional-weight (IFW) approach below.

Suppose the network dynamics withNinteracting nodes can be described by the following(N×M)-dimensional nonlinear equations of motion

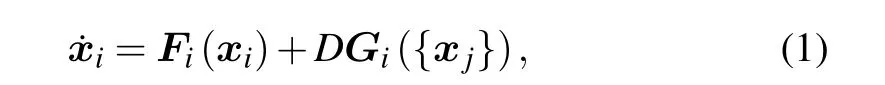
Assume that in the absence of coupling,i.e.,D=0, the dynamics of a single-node ˙xi=Fi(xi) possesses the stable fixed-point solutionx0i. For convenience, we setx0i=0 below. For the typical example of excitable models,e.g., the FHN and Bar models,one usually has a stable fixed point.

We are interested in the case of collective sustained oscillation of a network of non-oscillatory nodes. For all the nodes in a network that cannot oscillate independently, the oscillation of each nodeiis obviously induced by the interactions from its many neighbors represented by the nonlinear functionGi({xj}) in Eqs. (1). However, all the inputs from the neighbors to the target node are mixed together inGi({xj})by nonlinear functions.To measure the degree of contributions of different neighbors to the oscillation of the target node,contributions from all these neighbors should be separated. The basic idea of the functional-weight approach is to estimate the coupling significance of a node with other nodes by appropriately computing their weights,i.e., their individual contributions based on the coupling function.

Consider the coupling term of thei-th node in Eq.(1).The cross-differential “force” between thei-th and thej-th nodes(i/=j)can be measured by the time derivative of the variation of the coupling functionδ˙Gαi,j(x)as

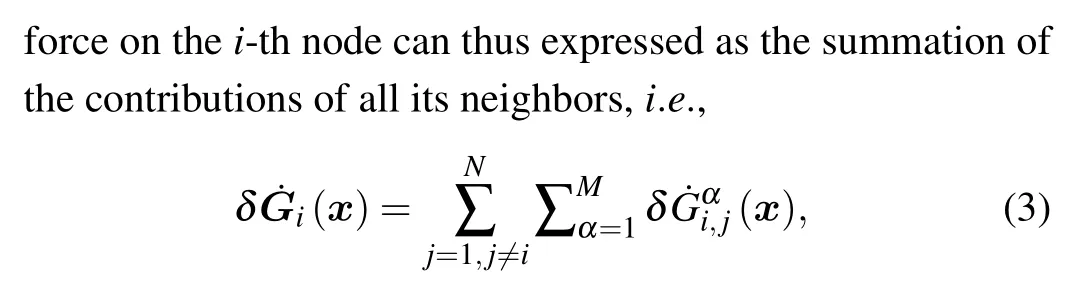
where the inner summation over the indexαfor components of the state,and the exterior summation is performed over the connected neighbors{j}of thei-th node.

The above relation indicates that the Jacobian differential form∂Gi(x)/∂xjrather than the nonlinear functionGi(x)itself plays a crucial role in the emergence of collective oscillations,because the amount of the variation of the target nodeicaused by the variation of a given neighborjdetermines the functional driving relationship fromjtoi.

We then can introduce the functional weightwi,j, which means the relative degree of influence of thej-th unit to thei-th unit,as the ratio of the cross differential force and the total force:

3. The B¨ar–Eiswirth network model

There have been a number of models in describing the excitable dynamics. Because one usually needs an excitable (fast) variable and a recovery (slow) variable to depict excitable dynamics, a minimal model should be a twodimensional dynamical system. Here one adopts the B¨ar-Eiswirth (BE)[32]model to describe the excitable dynamics.For a network of excitable units,the equations of motion ofNcoupled BE elements can be described by

The relaxation parameterε≪1 represents the time ratio between the activatoruand the inhibitorv. The dimensionless parametersaandbdenote the activator kinetics of the local dynamics,and the ratiouT=b/acan effectively control the excitation threshold.Dis the coupling strength between linking nodes.A={Ai,j}is the adjacency matrix,Ai,j=Aj,i=1 if there is a connection linking nodesiandj,andAi,j=Aj,i=0 otherwise.

Fig.1. (a)Phase diagram of the BE model,where the red lines are the nullcline f1(u,v)=0, and the blue lines are the nullcline f2(u,v)=0. Cross points A,B,C,and D are fixed points in the interval 0 ≤u ≤1,in which only the point A[(u,v)=(0,0)]is stable.(b)A schematic plot of the DPAD.As a comparison,the reference oscillatory time series,a usual PAD and a phaselagged dynamics are also presented,respectively.

The excitable property for the dynamics of the BE model can be briefly analyzed by resorting to the phase diagram given in Fig. 1(a), where the red and blue lines represent two nullclinesf1(u,v)=0 andf2(u,v)=0,respectively.The crossing points A,B,C,and D are fixed points,in which only the fixed point A [(u,v)=(0,0)] is the stable node, and fixed points B[(u,v)=(uT,0)]and C[(u,v)=(1,1)]are saddles,respectively,and the fixed point D is an unstable focus.An individual excitable node is non-oscillatory,i.e.,all nodes on the network may evolve asymptotically to the rest state (ui,vi) = (0,0),i=1,2,...,Nand will stay there perpetually unless some excitable drives push them away from this state. When the drive on one node exceeds the threshold B[(u,v)=(uT,0)],the excitable unit will first experience a global voyage in its phase space in the form of a large firing approaching the nullclineu= 1 and then the saddle C [(u,v) = (1,1)], followed by the evolution back to the vicinity of the nullclineu=0 and then its resting state A[(u,v)=(0,0)]. This typical excitability feature is common in other models. The transient instability leaves the possibility of a global and perpetual firings on the network when many excitable nodes are coupled with each other. This can be achieved by propagating a local firing to other resting nodes and eventually results in global selfsustained oscillations,which is the focus in this paper.

In the following,we perform numerical simulations of the excitable networks whose dynamics are described by Eqs.(10)and(11)for different network topologies. The parameters are fixed asa=0.84,b=0.07,ε=0.04,D=0.11. The threshold here isuT=b/a=1/12≈0.0833. Numerically, equations(10)and(11)are integrated by the Runge-Kutta integration algorithm with the time step Δt=0.01. Random initial conditions are adopted in the simulation.

4. Numerical results

4.1. The dominant phase-advanced driving approach

We will focus on the formation and propagation of oscillatory motion in excitable networks by using the IFW method proposed in Section 2. As a comparison, we also apply the dominant phase-advanced driving (DPAD) method to study the oscillation on networks.[29]Here we briefly recall the dynamical DPAD scheme. Given a network consisting ofNnodes withMlinks among these different nodes. One may clarify the significance of nodes in a network with sustained oscillations by comparing their phase dynamics. The oscillatory behavior of an individually non-oscillatory node is driven by signals from one or more interactions with advanced phases called the phase-advanced driving(PAD),if such a phase variable can be properly defined. The interaction giving the most significant contribution to the given node among all phaseadvanced interactions can be defined as the dominant phaseadvanced driving(DPAD).The corresponding DPAD for each node can be identified based on this idea,and by keeping these DPADs,the original network ofNnodes withMedges can be reduced to a one-dimensional unidirectional network of sizeNwithM＇≤Marcs.

An example of clarifying the DPAD is shown in Fig.1(b).The black curve denotes the given node as the reference node.Many nodes linking directly to this reference can be checked when a given network is proposed. Suppose there are three nodes whose dynamical time series labeled by green,blue and red curves,respectively. The green curve exhibits a lagged oscillation to the reference curve,therefore one calls it the phaselagged oscillation. The blue and red curves provide the drivings for exciting the reference node and are identified as PAD,among which the blue one that makes the most significant contribution should be the DPAD.

The DPAD structure reveals the dynamical relationship between different nodes. Based on this functional structure,we can identify the loops as the oscillation source, and illustrate the wave propagation along various branches. All the above ideas are generally applicable to diverse fields for selfsustained oscillations of complex networks consisting of individual non-oscillatory nodes.

4.2. Test on a ring of excitable sites

Let us first take on a test of the IFW approach in order to get a proper evaluation of the mutual impacts among different nodes. The simplicity of the ring topology is that it is symmetric so that one needs only to evaluate the impact of a node by computing the weights of the interactions from its two neighbors. For example, for thei-th node, we can study the functional weightswi,i±1and judge which one is larger.Ifwi,i+1＞wi,i-1, the propagation directioni+1→i →i-1 will dominant. Otherwise, ifwi,i+1＜wi,i-1, this implies that the propagation direction will bei-1→i →i+1.

In Fig.2,we present the preliminary test of oscillation on a ring with the sizeN=10 shown in Fig.2(a). A convenient way in introducing a sustained oscillation on a ring is as follows. One first deletes a link so that the ring becomes a chain.Then an external excitation can be added on one end node.The end node will be excited with a firing and then propagate along the chain by sequentially exciting its neighbors. One recovers the deleted link before the pulse reaches the other end of the chain. This will lead to a persistent and unidirectional propagation of the pulse along the ring. In Fig.2(b),the evolution of the componentsu5,6,7(t)are plotted. For such a sustained oscillation, in Fig.2(c), the functional weightsw6,5(t)andw6,7(t)are computed in terms of Eq.(8). It can be found thatw6,5(t) andw6,7(t) present the competition of the influence of nodesi=5 andi=7 on the nodei=6.To evaluate the overall weight,one plots the time-averaged functional weights¯w6,5and ¯w6,7. Unfortunately,it can be found that ¯w6,5≈¯w6,7,as shown in left two columns in Fig.2(d). This means that it is hard to distinguish the influences 5→6 and 7→6. Therefore,the average weight is not an appropriate quantity in distinguishing the propagation direction for the ring network.

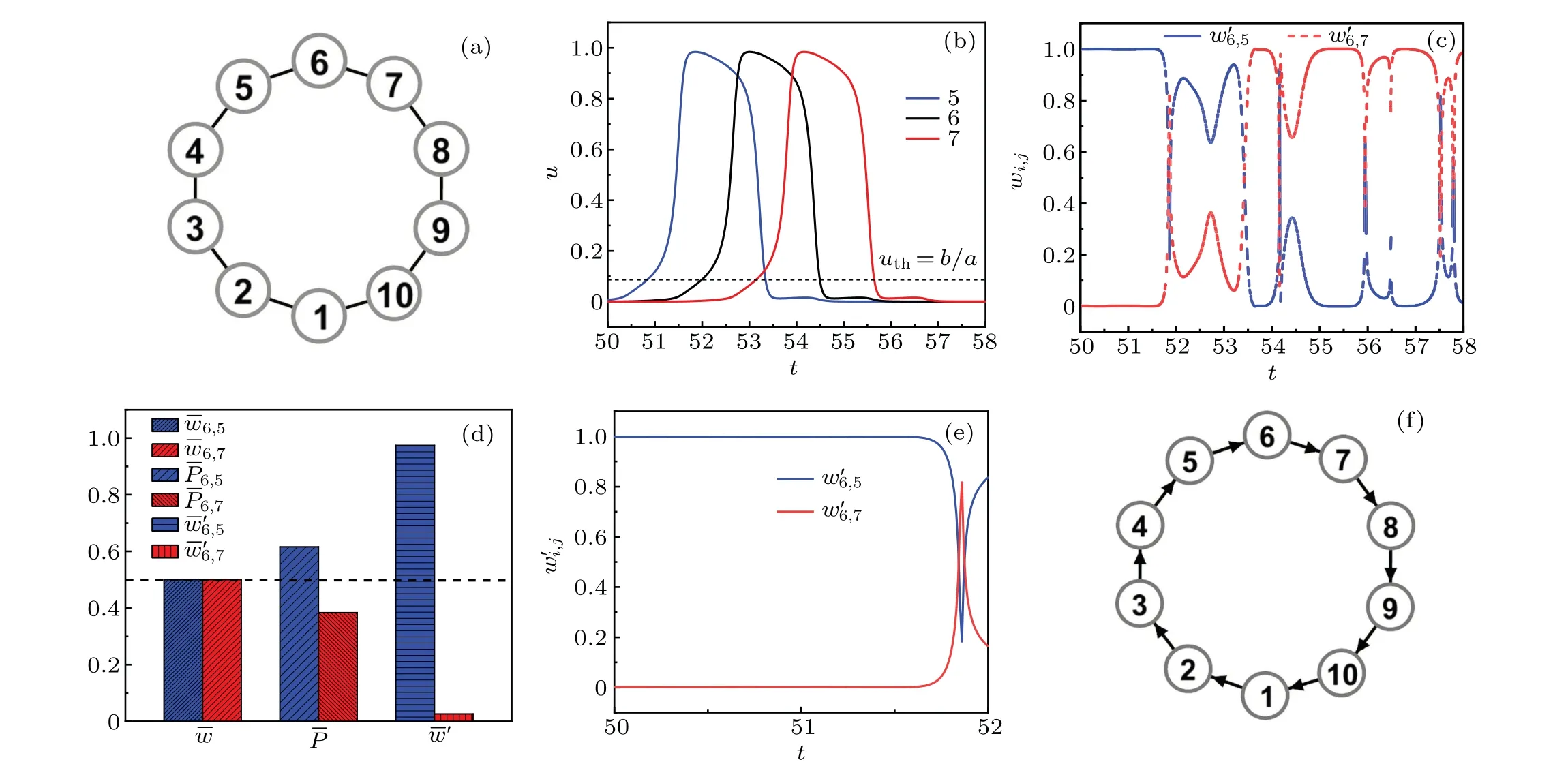
Fig.2. (a) The loop network composed of N =10 excitable nodes. (b) Time series of the components u5,6,7(t). (c) The evolution of the weight functions w6,5(t) (blue line) and w6,7(t) (red line). (d) Statistics of functional weights based on the time-average [¯w6,5 (blue), ¯w6,7 (red)], the occupation-rate [P6,5(blue),P6,7 (red)]approaches,and the partially-integrated approach[¯w＇6,5 (blue), ¯w＇6,7 (red)]. (e)The evolution of the weight functions w＇6,5(t)(blue line)and w＇6,7(t)(red line)when u(t)≤uth=b/a. (f)The propagation graph of the self-sustained oscillation.

To overcome the shortcoming of the averaged weight shown above, we adopt the weight occupation ratio defined by Eqs.(7)and(9). For the simple ring network in Fig.2(a),all nodes possess the same degreek=2, hence the threshold weight isw0=1/2. The right two columns present the ratioP6,5andP6,7,respectively. It can be clearly seen from the middle two columns of Fig.2(d)thatP6,5＞P6,7,which indicates that the impact from node 5 prevails that from node 7. In this case, the excitation will preferentially propagate via the path 5→6→7.

A distinct feature of sustained oscillation on excitable networks is the propagation of firing pulses along certain paths.This means that an excitable element stays at its stable point(resting state) until it is excited by a pulse, and a global excursion in phase space will occur if the element is excited beyond a threshold. The contribution of the functional weight will be the most significant in this region,i.e., it is unnecessary to compute the functional weight in an oscillation period for excitable dynamics. For the BE model adopted in this paper,the stable manifold of the saddle B act as the threshold of the all-or-none excitable behavior. Therefore,one needs only to compute the functional weight in the vicinity of the resting state,i.e., it is enough to perform the integral of Eq. (6)from the resting point (u0,v0)=(0,0) to the saddle threshold (uth,vth)=(b/a,0). In Fig. 2(b), we label the threshold by a horizontal dashed line. The behavior of the weight functionsw6,5(t)(blue line)andw6,7(t)are plotted in Fig.2(e). It is clearly shown thatw6,5(t)≈1 andw6,7(t)≈0 in this time interval. The averaged functional weight can be partially integrated as follows:

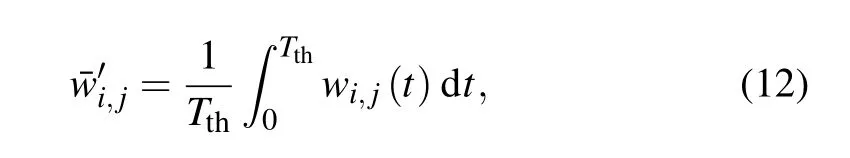
whereTthis the time satisfyingu(Tth) =uth=b/a. The partially-integrated average functional weights ¯w＇6,5(blue) ¯w＇6,7(red)are plotted as the right two columns of Fig.2(d). Obviously the dominant coupling direction is very clear.

By using the same procedure,for an arbitrary nodei,the above discussion gives the unidirectional propagation path of the pulse asi-1→i →i+1. The closed ring topology therefore adopts the Winfree loop shown in Fig. 2(f). Of course this wave direction depends on the initial condition. A simple symmetry analysis implies the existence of a reversed travelling path if the system starts from other initial conditions.The propagation path of the oscillation can also be obtained in terms of the DPAD approach. One can find that the IFW method shown in Fig. 2(d) agrees well with the DPAD approach.

4.3. Oscillation source and propagation path in homogeneous random networks

Let us further apply the improved functional-weight method to study the sustained oscillation in larger-scale networks. We first study excitable dynamics on the homogeneous random networks (HRN), whose degree distributionp(k) =δ(k-k0). This means that each node in an HRN has the same degreek0but each link is randomly given. Figure 3(a)gives an example of an HRN withN=20 nodes and degreek0=3. A typical sustained oscillation pattern by plotting the evolution ofui(t)(i=1,2,...,20)in Fig.3(b),where the white parts correspond to the firing process. By using the DPAD scheme, the propagation graph is plotted in Fig. 3(c).For this directed propagation network,each arrowi →jmeans the dominant drive and also the propagation direction of the oscillation fromitoj. One clearly finds a Winfree loop with 1→13→20→4→6→1.This loop is the source that generates and maintains the oscillation of the network.As a comparison,other nodes out of this loop only play the role of transferring the oscillatory pulses to their descending nodes and cannot form a closed loop. This can be conveniently tested by removing these nodes,and the same oscillation motion is still sustained on the loop, while the propagation to other nodes ceases.

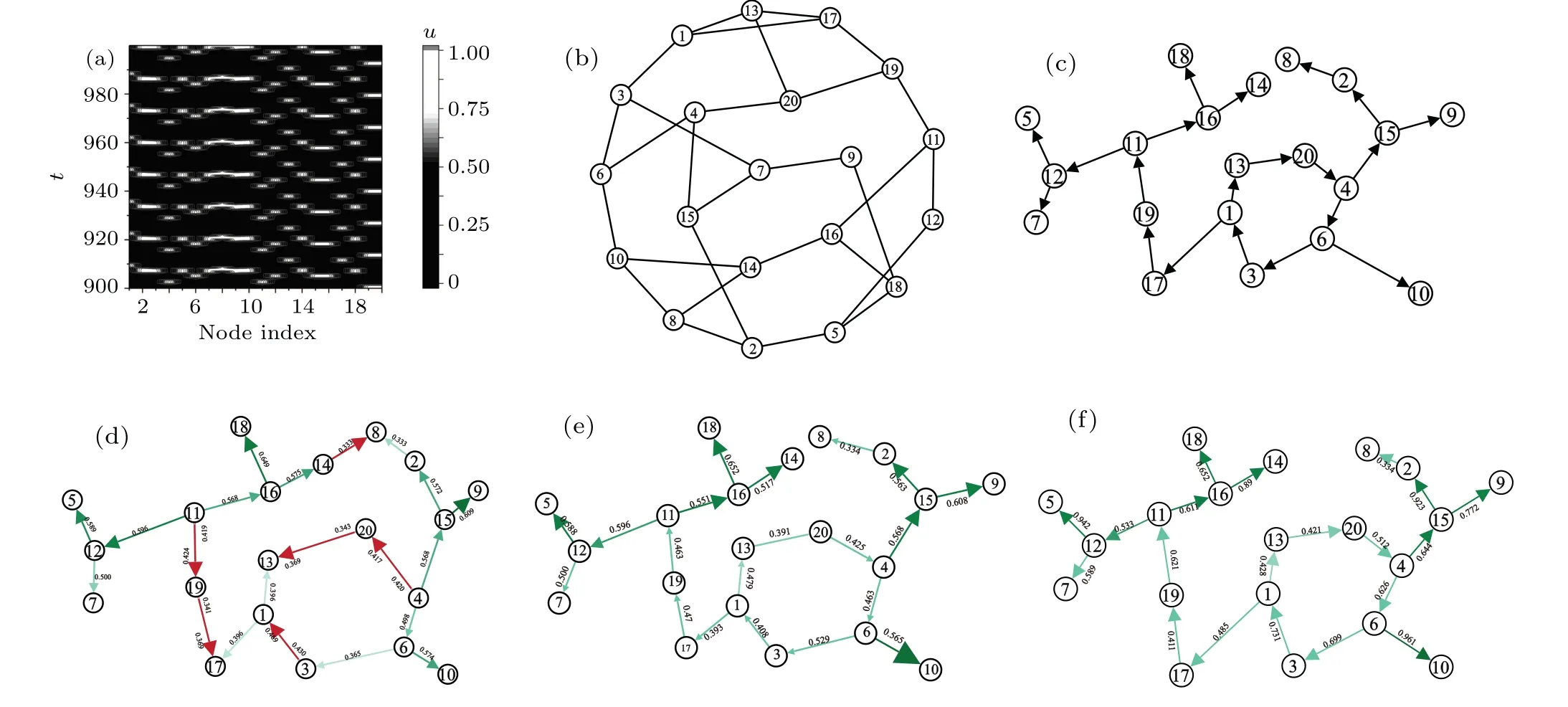
Fig.3. (a)A homogeneous random network with N=20 nodes and the degree k0=3. (b)Spatiotemporal dynamics of an example of sustained oscillation on the network given in panel(a). (c)The propagation graph obtained by using the DPAD approach. (d)The propagation graph obtained by using the average weight of the IFW approach, where some paths labeled in red are incorrectly judged. (e) The propagation graph obtained in terms of the occupation ratio of the IFW approach, which is in totally agreement with the DPAD scheme. (f)The propagation graph obtained in terms of the partially-integrated weight functional,which agrees totally with the DPAD scheme.

4.4. Multi-stable oscillation in excitable networks

A drastic feature of the sustained oscillations in excitable networks is the coexistence of a large number of oscillatory nodes and patterns. This indicates that if one starts from different initial conditions,one may find different oscillatory patterns. In Fig. 4, the left three columns (a), (c), (e) present three different spatiotemporal patterns by plotting the evolution of{ui(t), i=1,2...,n}starting from different initial states. A clear comparison between these different oscillation patterns needs revealing the Winfree loops and the propagation paths. By employing the IFW method, the propagation graphs of these three evolutionary states are obtained. It can be found that for the pattern in Fig. 4(a), the propagation graph in Fig. 4(b) reveals the Winfree loop of six nodes as 1→13→20→4→6→1, and other nodes serve as the propagation path of the wave. Also for the pattern 4(c), figure 4(d)gives the propagation graph with another 6-node Winfree loop with 2→15→4→6→1→8→2 as the oscillation source, and three paths are extended from different nodes on the loop. The oscillation pattern of Fig. 4(e) and its corresponding propagation graph in Fig. 4(f) reveal a longer Winfree loop with 2→8→14→16→18→9→7→12→5→2 and four stretched propagation paths,which implies a longerperiod(lower-frequency)oscillatory dynamics.

It should be emphasized that the above three patterns are only a small portion of patterns of sustained-oscillatory motion. However, the IFW method can distinguish all kinds of oscillation sources and possible propagation paths. In fact,all the Winfree loops are the topological loops embedded in the network that satisfy the oscillation condition. For a given network,there should be a number of loops. Due to the existence of many other nodes connecting with a given loop in different ways,the number of possible oscillation sources and paths should be huge. This is another intriguing topic that we will not discuss further here.

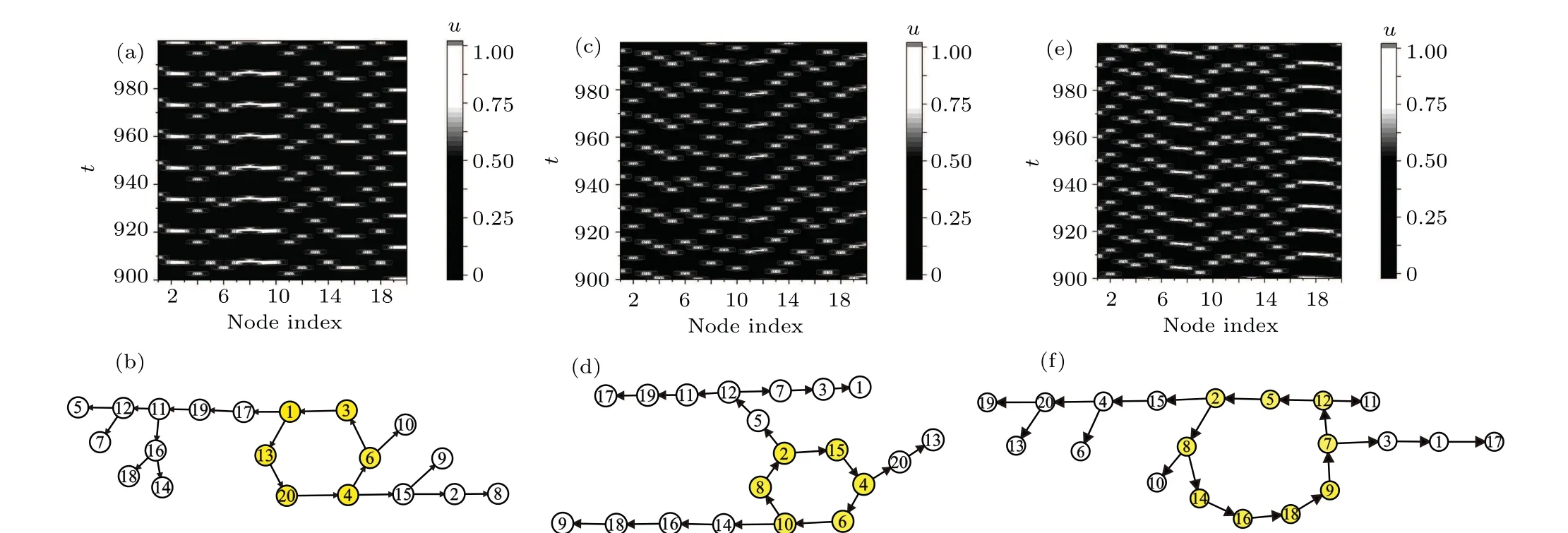
Fig.4. Explorations of propagation graphs of the three different random initial conditions for a uniform random network(N =20, k=3)in 3(a). (a), (c),and(e)The spatiotemporal evolution of three different collective oscillation modes;(b),(d),and(f)The propagation graphs corresponding to the dynamics in panels (a), (c), and (e), respectively, where shaded yellow nodes form the Winfree loop. The differences of spatiotemporal patterns are revealed as the distinction of propagation graphs with different oscillation sources and propagation branches.

4.5. Sustained oscillation in scale-free and small-world networks

Let us apply the IFW approach to explore the oscillation behaviors of other representative excitable networks such as the small-world1and scale-free networks2.In Fig.5,one studies the sustained oscillation of a Watts-Strogatz (WS) smallworld network, where a small-world network withN= 20 nodes and average degree〈k〉=4 is shown. This network is generated in terms of the WS scheme by starting from a regular network and randomly rewiring links with a probabilityp=0.3. A typical collective oscillation generated by yellow nodes{1,3,14,15,16}labeled in Fig.5(a)are studied and the propagation graph is given in Fig.5(b).

It can be found that the yellow nodes are self-organized in a directed Winfree loop and serve as the oscillation source.The generated oscillation is propagated from node No. 15 to No. 17, and then the pulses travel along two branches. More sub-branches are generated along the main paths. This is the typical pattern of the sustained oscillation on a homogeneous network.For homogeneous networks such as small-world networks,due to the homogeneity in the topology,one usually observes a moderate size loop and multiple bifurcations of propagation paths, which are responsible for the spreading of the oscillations among the network.

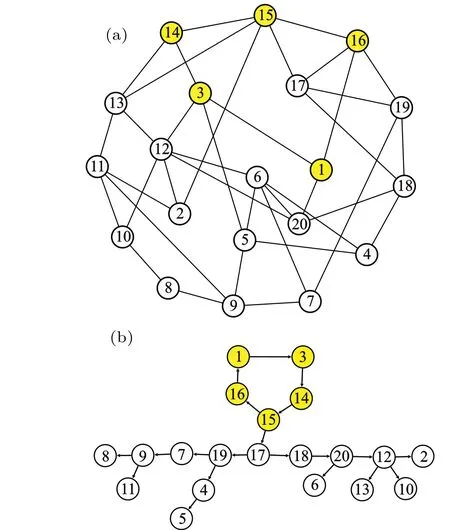
Fig.5. (a)A schematic topology of a WS small-world network with N=20 nodes by starting from a k=4 regular network and rewire with the probability p = 0.3. (b) The propagation path of the oscillation on the network obtained by the functional-weight method,where shaded yellow nodes{1,3,14,15,16}serves as the oscillation source,and the other nodes play as the propagator on the path.

Unlike uniform random networks, the interaction between nodes adopts the one-by-one excitation coupling form and belongs to a type of strong excitation to ensure that any rest node can be successfully exited by its any exciting neighbors. This type of interplay has been widely used in neural networks[33-35]and other excitable networks.[36-38]

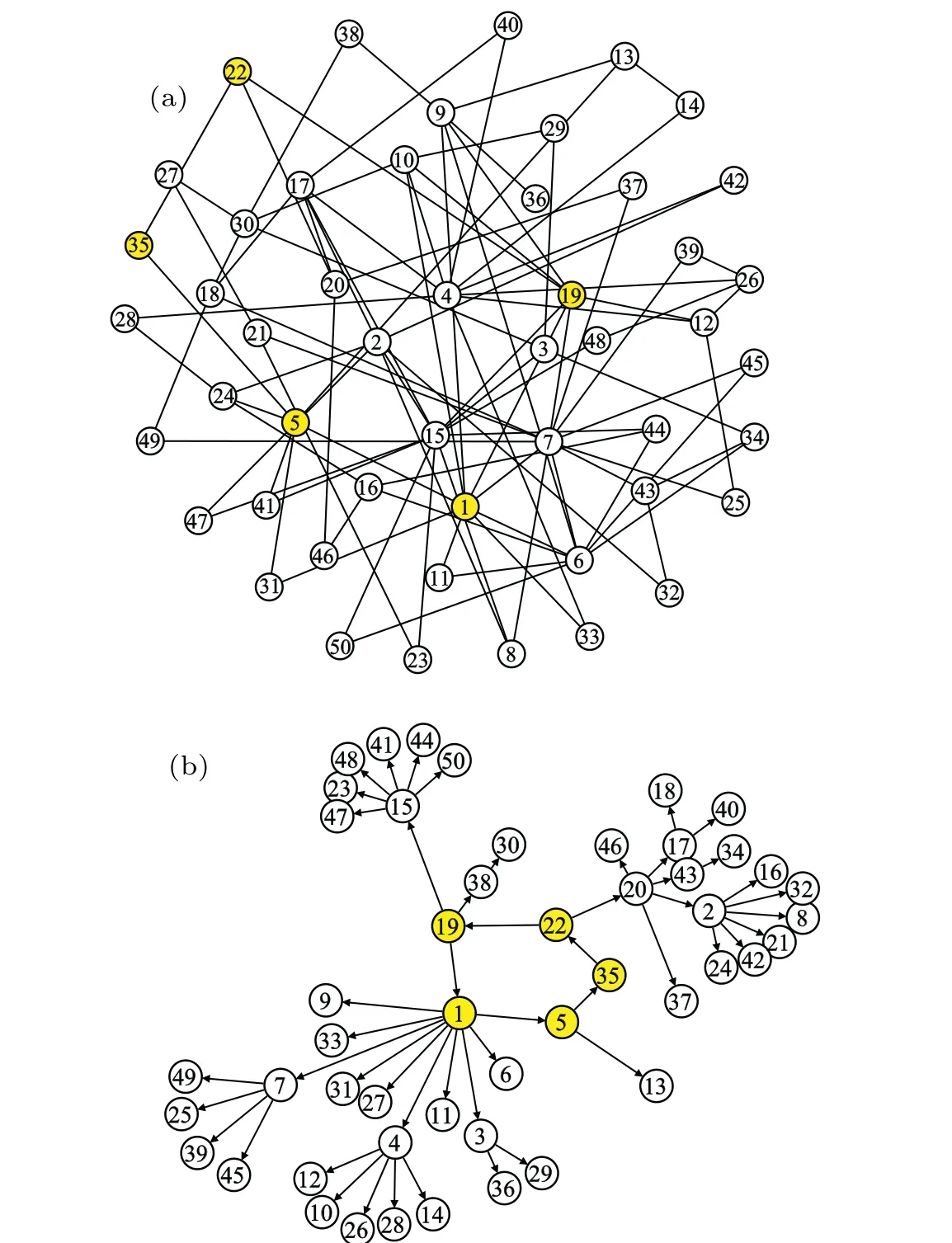
Fig. 6. (a) A schematic topology of a BA scale-free network with N =50 nodes, the number of links added at each step m=2, and the initial links m0 = 2, respectively. (b) The propagation path of the oscillation on the network obtained by the functional-weight method, where shaded yellow nodes{1,5,35,22,19}serves as the oscillation source,and the other nodes play as the propagator on the path.

As a contrast,it is interesting to investigate the property of propagation graphs for oscillation dynamics on heterogeneous networks. A typical class of networks with such properties are the scale-free networks. In Fig.6(a),a Barabasi-Albert(BA)scale-free network with parameters (N,m,m0)=(50,2,2) is plotted, whereN,m,m0are the number of nodes, number of links added at each step, and the initial links, respectively.The degree statistics of such BA network satisfies the powerlaw distributionP(k)∝k-γwithγ=-3,which is the typical scale-free property. Due to the existence of a few hubs with extremely large degrees,e.g., in Fig. 6(a), the largest three nodes and their degrees arek4=15,k1=13,andk2=10,respectively. The dynamics of the coupled BE nodes are slightly modified as

Figure 6(b) presents a typical propagation pattern of the self-sustained oscillation induced by yellow nodes{1,5,35,22,19}on the scale-free network shown in Fig.6(a)by using the IFW approach,where the coupling strengthD=0.45, and the constantK=1.8. Under the drive of this Winfree loop,the oscillation is propagated along many paths. This lacking of multiple hierarchies of bifurcation branches is originated from the heterogeneity property of the network. It can be found that most of the hubs with relatively large degrees are not located on the loop. They tend to distribute along different paths and form a number of star-like directed paths.This propagation pattern is much different from those homogeneous networks presented above(for example,see Figs.4 and 5(b)).

5. Concluding remarks

To summarize, in this paper we introduced the improved functional-weight approach by considering the highdimensional node dynamics to study the collective oscillatory motion on complex networks. By defining the dynamical weight, both the averaged weight and the occupation ratio statistics are introduced to evaluate the relative weights of different coupling direction and search for the dominant direction. This approach is applied to the study of sustained oscillations on networks of coupled excited nodes. By making comparisons with the DPAD method, it is shown that the IFW approach can successfully predict the propagation graph by using the occupation ratio statistics. We further studied the propagation graphs for homogeneous random networks,small-world networks,and scale-free networks in terms of the IFW approach and found distinct propagation topology properties for homogeneous and heterogeneous networks.

The merit of the IFW approach is that it can be well applied to reveal the basic building blocks of the collective dynamics on various networks. Because the functional weights are time-dependent, we expect that it can be applied to explore the emerging processes of collective oscillations, especially the competition dynamics. For the sustained oscillations of excitable networks, there exist a lot of potential candidates of Winfree loops. Different loops correspond to different dynamical oscillation modes with different phases and frequencies.[39]These loops will compete with each other,and eventually only a very few modes will survive. We believe the improved functional-weight method can be a promising approach in detecting these competition processes. This will be our future subject.

Acknowledgement

Project supported by the National Natural Science Foundation of China(Grant No.11875135).