卢行远，侯忠生

(青岛大学自动化学院，山东青岛 266071)

1 引言

20世纪50年代以来，基于模型的控制理论得到了快速的发展与完善.但随着受控系统越来越复杂，系统精确模型不易建立或建模成本过高、未建模动态与模型不确定性难以避免、理论分析结果与实际应用效果间存在鸿沟等问题逐渐显现[1-3].为摆脱基于模型进行控制器设计所带来的局限性，近年来数据驱动控制(data driven control，DDC)方法吸引了广泛关注[4-7].

无模型自适应控制(model free adaptive control，MFAC)是一种典型的数据驱动控制方法，由侯忠生教授于1994年提出[8].针对离散时间非线性系统，MFAC原创性地提出了伪偏导数(pseudo partial derivative，PPD)的新概念，并给出了一种新的动态线性化方法.其控制器设计不依赖于系统数学模型，只需用到受控系统的在线输入输出(input/output，I/O)数据，即可实现系统的参数自适应控制和结构自适应控制[9].到目前为止，文献[9-12]已给出了完整的基于紧格式动态线性化(compact form dynamic linearization，CFDL)、偏格式动态线性化(partial form dynamic linearization，PFDL)、全格式动态线性化(full form dynamic linearization，FFDL)的MFAC控制方案和严谨的稳定性证明.相比基于模型的控制方法，MFAC方法具有无需建模、计算简单、易于实际应用等优势[13].

鲁棒性是现代控制系统的一个重要设计指标，是控制系统能否真正实际应用的关键.不同于基于模型的控制方法，MFAC方法由于无需系统模型，仅利用系统在线I/O数据进行控制器设计，所以传统基于模型不确定性而定义的鲁棒性在MFAC理论中失去了意义[14].而从数据的角度考虑，受控系统的I/O数据是MFAC控制器的设计依据，所以数据的准确与否将显著影响MFAC方法的控制效果.因此，MFAC理论的鲁棒性问题是从系统在何种程度的数据噪声、数据丢失下仍能保持原有性能来考虑的[15].在实际工业过程中，由于传感器测量误差、传输过程中各种噪声等原因导致的测量扰动是无法避免的.因此，本文就无模型自适应控制方法的测量扰动抑制问题进行研究.

针对无模型自适应控制方法测量扰动抑制问题，现有方法可以分为两类.第1类方法从改进MFAC控制律角度考虑.文献[15-16]分别通过在MFAC控制律中引入死区环节、衰减因子，使得控制算法在一定情况下停止更新，以实现对测量扰动的抑制.此类方法在跟踪常值参考信号时扰动抑制效果较好，但在参考信号时变时此类方法的控制效果则有待改善，且此类方法存在误差阈值难以选定的问题[16].第2类方法从对噪声数据进行滤波角度考虑.文献[17]通过引入低通滤波器，先将高频测量噪声滤除，然后将滤波后的数据输入MFAC控制器，但工业中最常见的白噪声频率丰富，没有确定的频谱[18].文献[19]利用跟踪微分器的滤波能力，将其与MFAC控制器进行模块化设计，实现了测量扰动的抑制.但跟踪微分器的引入会使信号产生相位损失[20]，影响到控制器的响应速度，且其效果仍有提升空间.文献[21]将多个传感器测得的数据进行卡尔曼滤波和融合处理后送入MFAC控制器，相比于使用单一传感器的测量数据，该方法可显著提高数据精度，但增加了系统复杂性及控制成本.基于以上原因，探究更有效易用的测量扰动抑制方法，提升无模型自适应控制方法在实际应用中的抗扰控制性能有重要意义.

卡尔曼滤波是当前应用最为广泛的滤波方法，已经在通信、导航、制导等多领域得到了成功应用[22-25].然而卡尔曼滤波器实现滤波过程需要已知系统的精确数学模型，而在无模型自适应控制方法中，由于控制对象是一大类模型难以建立的系统，所以经典卡尔曼滤波器无法直接嵌入到MFAC方法当中[26].借鉴卡尔曼滤波器的设计思路，本文针对MFAC方法中测量扰动抑制问题，推导并提出了一种改进的卡尔曼滤波器.可以在受控系统模型未知的情况下，实现对含噪声输出数据的滤波.然后基于此改进的卡尔曼滤波器，进一步设计了基于改进卡尔曼滤波器的扰动抑制MFAC方案.相比现有的扰动抑制MFAC方案，新方案具有适用性强，整定参数少，实现成本低等优点，不同参考信号形式下的仿真跟踪实验验证了所提算法的有效性.

2 问题描述

本节首先以基于紧格式动态线性化的无模型自适应控制(CFDL-MFAC)为例，简要介绍MFAC方法的控制方案及有关概念.然后在此基础上，分析现有方案的不足并提出本文所要解决的问题.

考虑如下一般SISO非线性离散时间系统:

其中:u(k)∈R和y(k)∈R分别表示系统在k时刻的I/O数据，nu，ny是两个未知的正整数，f(···)是未知的非线性函数.对系统(1)做出如下两个假设.

假设1除有限时刻点外，f(···)对u(k)存在连续偏导数.

假设2系统满足广义Lipschitz条件，即对任意k12，k1，k2≥0和u(k1)(k2)有

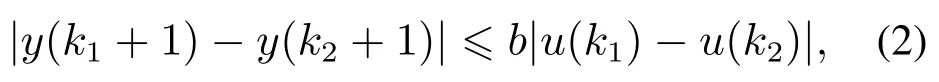
其中y(ki+1)f(y(ki)，···，y(ki-ny)，u(ki)，···，u(ki-nu))，i1，2，b ＞0是一个常数.

记Δy(k)y(k)-y(k-1)为相邻两个时刻的输出增量，Δu(k)u(k)-u(k-1)为相邻两个时刻的输入增量.

定理1对满足假设1，2的非线性系统(1)，当Δu(k)0时，一定存在一个被称为PPD的时变参数φc(k)∈R，使得

且φc(k)对任意时刻k有界.

定理1的详细证明过程可参考文献[9].

由定理1可得系统(1)的紧格式动态线性化数据模型为

若存在数据测量扰动的作用，则系统输出测量值为

其中测量扰动|d(k)|≤dm，dm为正的常数.

此时，CFDL-MFAC控制方案为

其中:Δym(k)ym(k)-ym(k-1)，ε为极小正数，λ ＞0，μ ＞0为权重因子，ρ ∈(0，1]，η ∈(0，1]为步长因子.PPD重置算法(7)的作用是使PPD估计算法(6)对时变参数有更强的跟踪能力.

由控制律(8)可知，MFAC控制器基于输出误差反馈进行控制，其控制量更新依赖于系统的输出测量值ym(k).当系统不存在测量扰动时，常规MFAC方案可使系统输出误差收敛至0[9]，当系统存在测量扰动时，应用常规MFAC方案，系统的输出误差将会收敛到一个关于dm不为0的常数[17].因此，测量扰动的存在会显著恶化常规MFAC方案的控制性能.

3 基于改进卡尔曼滤波器的扰动抑制MFAC算法

本节首先借鉴卡尔曼滤波器的设计方法，推导并提出基于系统I/O数据的改进卡尔曼滤波器，然后基于此改进的卡尔曼滤波器，给出新的扰动抑制无模型自适应控制方案.

3.1 改进的卡尔曼滤波器

卡尔曼滤波(Kalman filter，KF)采用状态空间法在时域内设计滤波器，其本质是一种最优递推数据处理算法.在线性系统中，卡尔曼滤波器是最优滤波器[18]，其最优性体现在使得估计误差的均方误差达到最小，即最小方差估计[26].

卡尔曼滤波器用状态方程描述系统的动力学特性[27]，其实现滤波过程需要已知系统的精确数学模型.然而在实际应用中，无模型自适应控制方法的控制对象是一大类模型难以建立的系统.因此，使用动态线性化数据模型替代状态方程，设计如下改进的卡尔曼滤波器(improved Kalman filter，IKF).

考虑由如下数据方程描述的一般SISO非线性离散时间系统:

其中:y(k)∈R，u(k)∈R为系统I/O数据，(k-1)∈R为伪偏导数估计值，w(k)∈R为数据过程噪声，v(k)∈R为数据测量噪声.对系统(9)做如下假设.

假设3w(k)和v(k)是均值为0，方差分别为Q和R的不相关白噪声，即

注1式(9)利用CFDL数据模型对真实输出数据做一步向前预测，由于PPD解析式未知，采用估计算法得出，其中各因素造成的参数不确定性、数据模型误差由过程噪声w(k)表达.

注2上述假设并不苛刻，对于实际环境中概率分布未知且来源复杂的噪声复合体，高斯型白噪声是对其合理的近似，这与经典卡尔曼滤波器对噪声性质的假设一致.

引理1线性最小方差估计具有线性性质.若被估量x在量测量z上的线性最小方差估计为E*[x/z]，则Fz+e在z上的线性最小方差估计为

其中:F为确定性矩阵，e为确定性向量.该引理的详细证明过程可参考文献[18].

定理2在给定初始输出估计值(0|0)μ(0)及初始误差方差P(0|0)P(0)后，系统(9)在假设3下，递推IKF设计如下:

输出数据一步预测

一步预测误差方差

计算IKF增益

输出数据最优估计

更新估计误差方差

证一步预测是根据k-1时刻的估计值预测k时刻的输出值，即根据k-1个测量数据{ym(1)，ym(2)，···，ym(k-1)}对y(k)做线性最小方差估计

由引理1，有

由式(9)可知，过程噪声w(k-1)与测量数据ym(k)不相关，且由假设3有E[w(k)]0.因此，有输出数据一步预测值

用一步预测值代替真实输出值，引起的误差为

引起对测量的估计误差为

em(k|k-1)又称为残差.

残差包含一步预测误差信息，对其作加权处理，用来修正一步预测值(k|k-1)，可得输出数据的估计

其中K(k)∈[0，1]为对残差的加权系数，即滤波器增益系数.

定义估计误差e(k|k)y(k)-增益系数K(k)的选取准则是使估计的均方误差P(k|k)E[e(k|k)2]最小.由式(9)(21)有

由上式及假设3，有

其中:

由式(23)对K(k)求导并令其等于零，可得滤波增益K(k)

进一步的，用K(k)表达式简化式(23)

至此，综合式(18)(21)(25)-(27)，可得递推IKF滤波方程组. 证毕.

由上述推导可知，IKF中两个主要可调参数，过程噪声方差Q和观测噪声方差R的比值关系决定了滤波增益K(k)的大小，并进一步决定了数据模型预测值ˆy(k|k-1)和数据观测值ym(k)占滤波值ˆy(k|k)权重的大小，两个参数的不同组合对系统的影响将在第4节得到进一步讨论.

3.2 基于IKF的扰动抑制MFAC算法

本节提出基于改进卡尔曼滤波器的扰动抑制无模型自适应控制方案，将IKF与MFAC方法结合，实现对数学模型未知且存在测量扰动的系统的控制.算法结构如图1所示.

图1 基于IKF的扰动抑制MFAC算法结构Fig.1 Structure of the MFAC with disturbance attenuation based on IKF algorithm

IKF-MFAC方案在每一时刻根据数据模型及测量扰动的统计特性计算滤波增益，对传感器测量值ym(k)及模型预测值ˆy(k|k-1)做合理加权平均，计算得到滤波输出值ˆy(k|k)后再输入MFAC控制器进行系统控制.该方案避免了常规MFAC 方法直接使用数据测量值ym(k)进行控制器设计易受测量扰动影响的问题，且由于ˆy(k|k-1)来源于数据模型预测，所以相比于文献[21]，该方案无需增加额外的数据测量设备.

结合图1，给出如下完整的IKF-MFAC控制方案:

该算法实现步骤如下:

1) 利用IKF的滤波能力，基于上一时刻的系统输入数据及输出最优估值预测得到当前时刻的输出预测值(k|k-1)，计算IKF增益并利用当前时刻的输出测量值ym(k)进行校正，得到系统当前时刻的输出最优估值ˆy(k|k).

3) 将控制算法(35)作用于被控系统，得到新的数据对{u(k)，ym(k+1)}，然后重复步骤1.如此循环，直至系统的输出逼近期望信号y*，完成控制过程.

4 仿真研究

为验证基于IKF的扰动抑制MFAC方案的有效性，考虑在多种噪声水平下对两类参考信号的跟踪问题，本节给出基于IKF的MFAC方案、带有衰减因子的MFAC方案(MFAC with decreasing gain，D-MFAC)和带有跟踪微分器的MFAC 方案(MFAC with tracking differentiator，TD-MFAC)的仿真对比实验.

D-MFAC采用如下控制算法[16]:

其中:跟踪误差e(k)y*(k+1)-ym(k)，em为设定的误差阈值，km为跟踪误差e(k)从|e(k)|≥em(k)到|e(k)|＜em的切换时刻.带有衰减因子的MFAC方案预先设定一个误差阈值，在跟踪误差较大时执行常规MFAC方案，使跟踪误差先收敛至|e(k)|＜em，然后衰减因子开始发挥作用.由于测量扰动是通过误差e(k)引入的，因此随着k的增加，测量扰动将得到抑制[16].

TD-MFAC利用跟踪微分器的滤波能力，让系统的输出信号先通过跟踪微分器，得到经过去噪处理的信号x1，然后再将误差信号e(k)y*(k+1)-x1作用于MFAC控制器[19].跟踪微分器的离散化公式为[28]

其中:x1(k)用于跟踪输入信号u(k)，x2(k)用于跟踪输入信号的导数，h为积分步长，r为决定跟踪速度的速度因子，h0为滤波因子.适当缩小积分步长h或者扩大滤波因子h0可以增强跟踪微分器的滤波效果[29].fhan(x1(k)，x2(k)，u(k)，r，h0)为最速控制综合函数.其算法公式可参考文献[29].

为便于对3种方案的控制性能进行比较，定义跟踪误差绝对值e*(k)|y*(k)-y(k)|，并使用均方根误差(root mean square error，RMSE)和信噪比(signal noise ratio，SNR)两个指标对3种方案的控制性能做直观描述，两指标表示为

RMSE计算系统实际输出与期望输出在每时刻差异，其值越小，系统跟踪效果越好.SNR表示有用信号与噪声的功率谱比值，由于功率谱不易计算，故采用信号与噪声的方差之比估计SNR.其值越大，系统去噪与控制的综合效果越好.

例1考虑如下SISO非线性系统

首先，对IKF中可调参数Q和R的比值关系对IKFMFAC方案的控制性能影响进行验证.如图2所示.

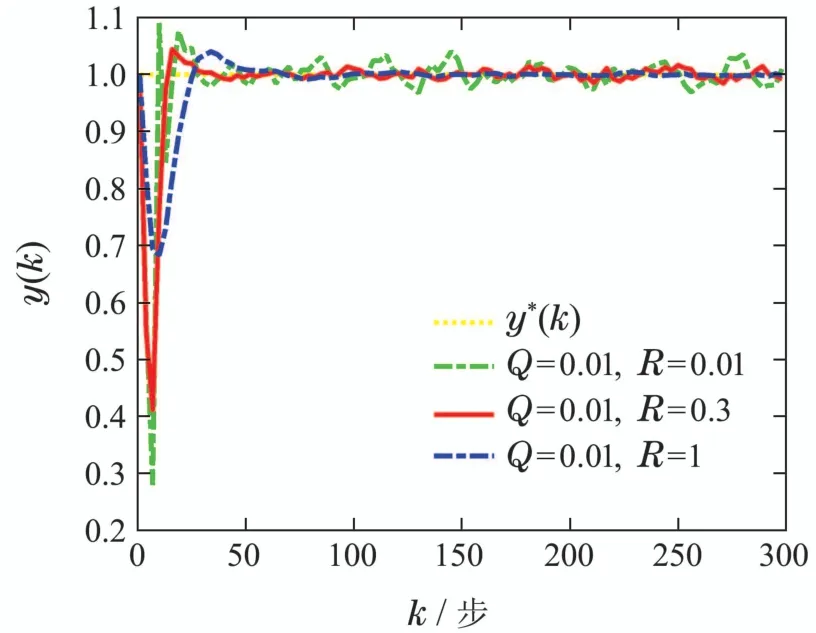
图2 不同参数组合对IKF-MFAC方案控制性能影响Fig.2 Influence of different parameter combinations on IKF-MFAC scheme control performance

由上图，在测量噪声不变的情况下，固定过程噪声方差Q，逐渐增大观测噪声方差R，IKF-MFAC方案的抗扰控制能力逐渐增强，但相应的控制器响应速度逐渐下降.原因在于观测噪声方差R表征了数据测量精度，增大R意味着增大测量扰动的影响，减弱系统校正权值，数据模型预测值占滤波值权重增大.相应的，过程噪声方差Q表征了动态线性化数据预测模型的统计特性，增大Q等价于增加模型预测的不确定性，加大系统的校正权值，数据实际测量值占滤波值的权重将会增大.

经多次调试，选取3种方案最优参数，TD-MFAC选取快速因子r1800，积分步长h0.001，滤波因子h00.0018.D-MFAC选取误差阈值em0.28.3种方案的抗扰跟踪控制性能对比如下.

由图3-4可知，测量扰动的存在会显著恶化常规MFAC方案的控制性能，使系统输出产生明显抖动，其中k500，k750时刻的输出抖动是由于系统结构变化及时变参数r(k)导致的.相比常规MFAC方案，TD-MFAC方案可有效抑制测量扰动的作用，但是输出抖动仍然存在且系统的响应速度有所下降.原因在于跟踪微分器平滑扰动信号以信号相位损失为代价，信号越平滑，滞后现象就越严重[28].D-MFAC方案通过引入衰减因子，虽然可以有效抑制测量扰动的作用，但也会使控制量在一定时刻后几乎停止更新，易使系统输出产生静差.

图3 常值参考信号跟踪性能比较Fig.3 Comparison of tracking performance under constant reference signal

例2进一步的，对于参考信号时变情况下的跟踪控制，考虑如下SISO非线性系统:

参考信号为

图4 常值参考信号跟踪误差绝对值比较Fig.4 Comparison of absolute value of tracking error under constant reference signal

增大测量噪声为v(k)1×randn(1，800)，控制器参数设定类似例1，调整TD-MFAC方案快速因子r1450，积分步长h0.0035，滤波因子h00.003.D-MFAC选取误差阈值em2.28.IKF-MFAC假定过程噪声方差Q0.15，测量噪声方差R0.75，3种方案的抗扰跟踪控制性能对比如下.

由图5-6可知，参考信号为时变信号时，D-MFAC方案控制效果显著下滑.原因在于时变的参考信号使系统输出无法进入稳态，何时引入衰减因子的作用，即误差阈值em的选取就变得极为困难.小的em无法起到抑制测量扰动的作用，而大的em又会使系统输出呈现阶梯状，失去平滑.这一情况下考虑对扰动信号进行滤波的TD-MFAC方案和IKF-MFAC方案更具优势.

图5 时变参考信号跟踪性能比较Fig.5 Comparison of tracking performance under timevarying reference signal

综合上述两例，使用RMSE与SNR两指标对3种方案抗扰控制性能做直观描述，结果如表1所示.

通过图3-6及表1数据分析可知，本文给出的IKFMFAC方案相比于现有的扰动抑制MFAC方案，在各类参考信号及噪声水平下均能更有效地抑制数据测量扰动，算法适用性更好的同时具有更小的跟踪均方根误差及更大的数据信噪比，可以显著提升MFAC方法在数据测量扰动环境下的控制性能.

图6 时变参考信号跟踪误差绝对值比较Fig.6 Comparison of absolute value of tracking error under time-varying reference signal

表1 3种扰动抑制MFAC方案控制性能比较Table 1 Comparison of control performance of three disturbance attenuation MFAC schemes

5 结论

本文针对MFAC方法在数据测量扰动作用下控制效果不佳的问题，基于受控系统的动态线性化数据模型，首先提出了一种基于系统输入输出数据的改进卡尔曼滤波器，然后将其与基本MFAC方法相结合，给出了IKF-MFAC抗扰控制方案，并对算法的抗扰控制性

能与现有方案做了综合对比分析.针对不同形式的参考信号仿真跟踪结果表明，与现有的抗扰MFAC方案相比，IKF-MFAC具有更小的跟踪均方根误差及更大的数据信噪比，且兼具适用性强，整定参数少，实现成本低等优点，可以显著提升MFAC方法在实际应用中的抗扰控制性能.