非线性SRLW方程的二重网格块中心有限差分方法❋
2022-09-05谢树森
许 洁, 谢树森
(中国海洋大学数学科学学院, 山东 青岛 266100)
1984年,Seyler通过对弱非线性作用下等离子声波和空间电荷波的传播的分析,提出了正则长波方程的对称描述,即对称正则长波(Symmetric regularized long wave,SRLW)方程[1]:
一般情况下,通常无法得到此类非线性模型的解析解。因此,数值方法成为研究SRLW方程的一个重要手段。
关于SRLW方程的数值方法已经有了一些相应的研究。1987年,郭柏灵[2]用谱方法研究了一类SRLW方程的周期边值问题。1989年,郑家栋等[3]对SRLW方程提出了带约束算子的Fourier拟谱方法,并证明了该方法的稳定性和最优误差估计。1995年,任宗修[4]考虑了SRLW方程的Chebyshev拟谱方法,构造了半离散和全离散Chebyshev拟谱格式,并得出了相应的误差估计。2003年,尚亚东和郭柏灵[5]分析了多维广义SRLW方程的Chebyshev拟谱格式。2006年,孔令华等[6]用时间上的Euler中点格式和空间上的Fourier拟谱方法对SRLW方程构造了一个多辛Fourier拟谱格式,并证明了该格式的离散守恒定律。
块中心有限差分法(Block-centered finite differe-nce,BCFD)又称为单元中心有限差分法,通过采用适当的数值求积公式,可以认为是最低阶的Raviart-Thomas混合元法[7]。Weiser和Wheeler[8]研究了一维和二维矩形区域中带Neumann边界条件椭圆问题的BCFD方法,证明了在足够光滑的条件下,对于所有非均匀网格,所求椭圆问题的近似解及其一阶导数中张量积BCFD的离散L2范数误差都是二阶的。在文献[9]中,Arbogast、Wheeler和Yotov提出了以张量系数为块中心差分的椭圆问题的混合有限元方法。此外,文献[10-14]分别提出了求解多尺度流动问题、半导体器件问题、含时间变系数抛物方程、对流-扩散问题和海水入侵问题的BCFD方法。BCFD方法在一般非均匀空间网格上具有超收敛性,对未知量及其导数都能保持二阶空间精度。因此,它被广泛应用于边界层和大梯度变形问题。
1996年,许进超[15]提出二重网格(Two-grid,TG)法思想,这种方法可以看作是一种两层预测校正方法。二重网格法不是在细网格上求解大规模非线性问题,而是在粗网格上求解小规模非线性系统,在细网格上求解大规模线性系统,这样在保证良好稳定性的同时,又减少计算量。因此,如文献[16-18]所示,TG方法由于其高效性和有效性,特别是在非线性模型的大规模建模和仿真方面,受到了广泛的关注。
本文给出了Crank-Nicolson二重网格块中心有限差分(CN-TG-BCFD)的全离散格式。对模型进行了数值实验,验证了该方法在均匀和非均匀网格上的二阶收敛性。将CN-TG-BCFD格式得到的结果与Crank-Nicolson完全非线性块中心差分(CN-BCFD)方法比较,两者在同一离散范数下具有相同量级的误差,但CN-TG-BCFD方法效率更高,且在计算大规模问题中更明显。
1 问题及记号
上述SRLW方程可写成如下等价形式:
(1)
其中(x,t)∈I×J:(a,b)×(0,T]。 边界和初值条件分别为
ux(a,t)=ux(b,t)=ρ(a,t)=ρ(b,t)=0,t∈J,
其中u0(x)和ρ0(x)为两个已知的光滑函数,其中ρ和u分别是无量纲电子电荷密度和流体速度[13]。该系统描述了弱非线性(1+1)维离子声波和空间电荷波。


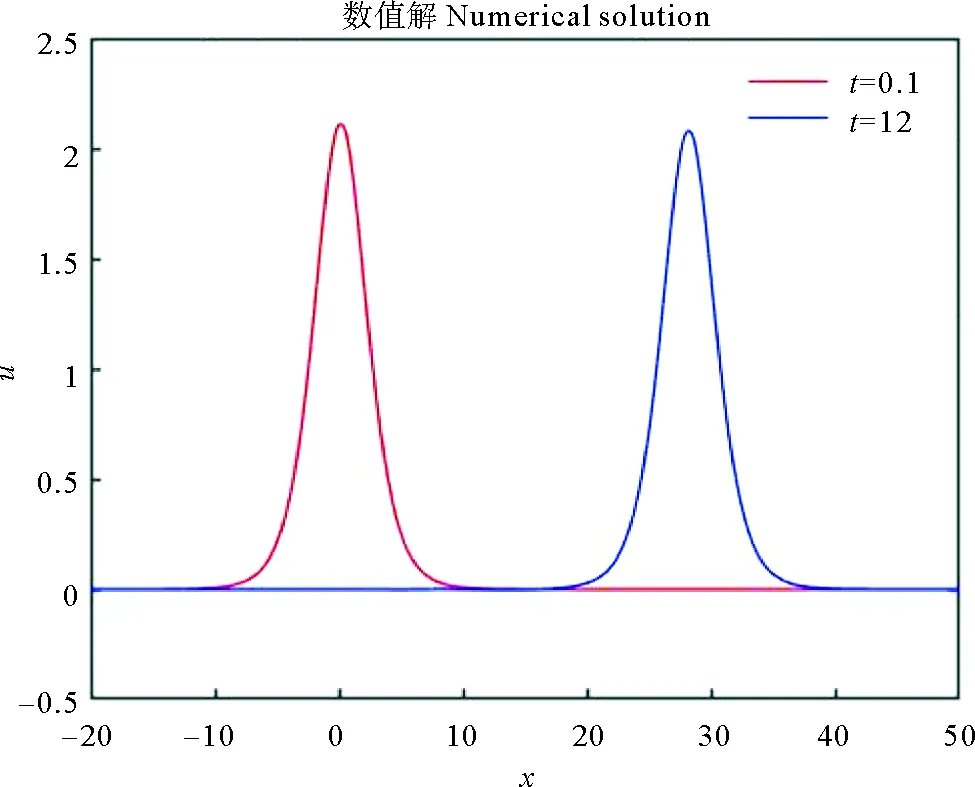
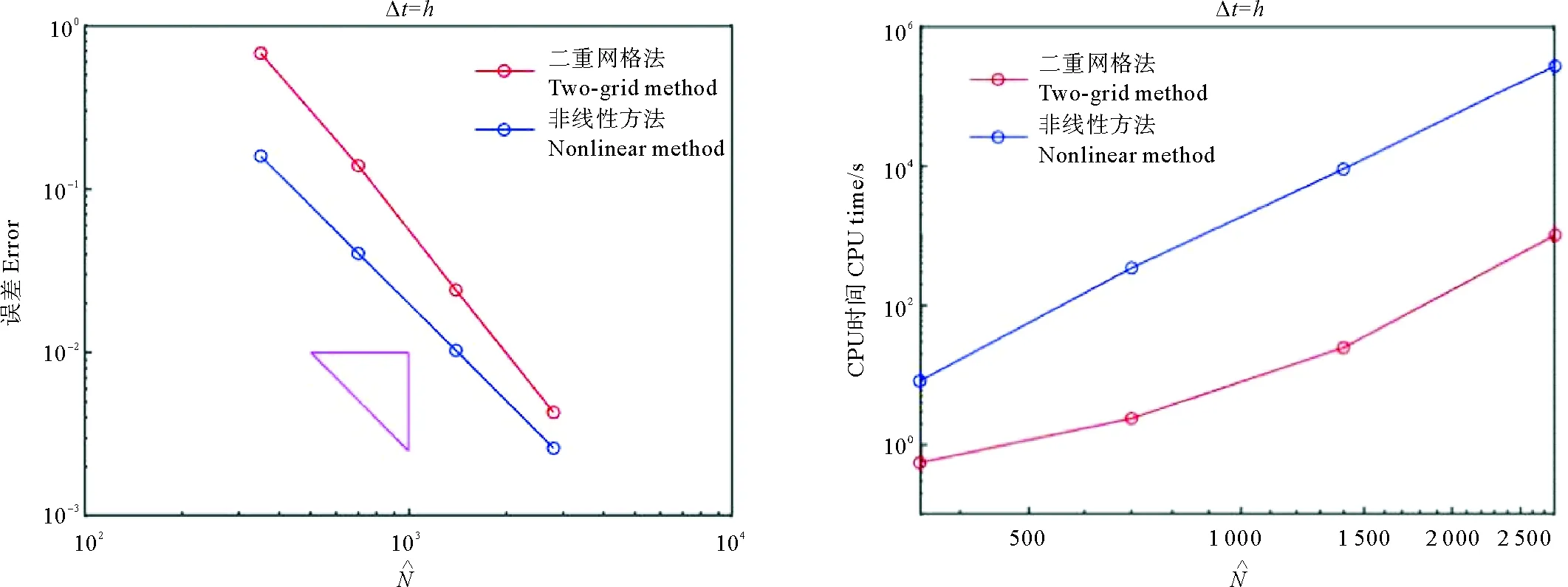
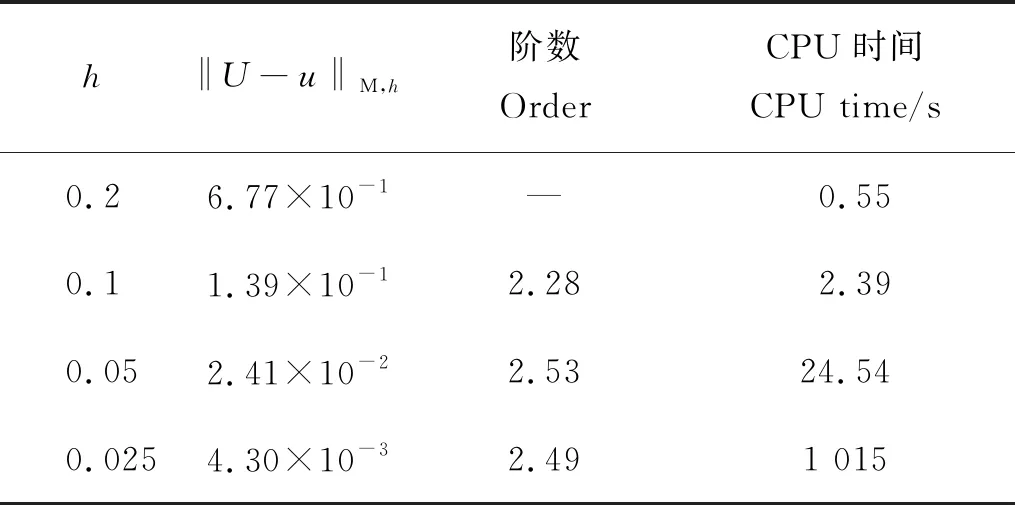
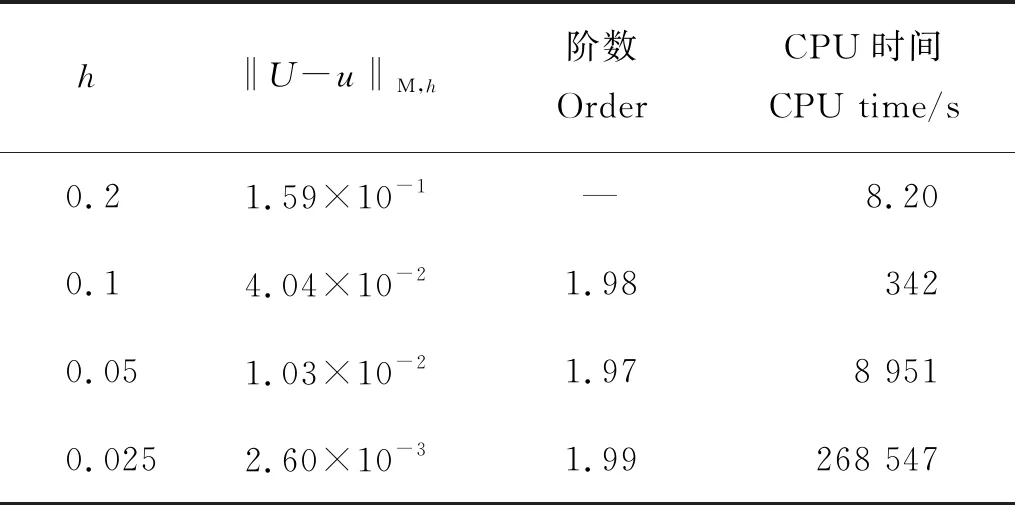
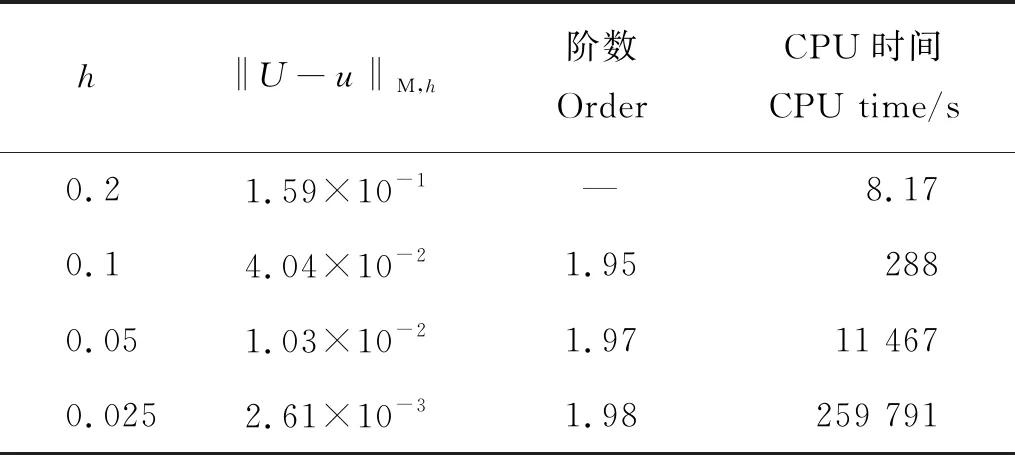
πH:a=x1/2 假设网格划分是正则的,即存在一个正常量σ,使得 在粗网格上,定义如下离散内积和范数 ΠHv(x)定义为v(x) 的分段线性插值: x∈[xi,xi+1],1≤i≤N-1。 ΠHv(x1/2) 定义为: 定义 LHv(x)为v(x) 的分段线性插值: x∈[xi-1/2,xi+1/2],1≤i≤N。 令p=-ux,则式(1)等价写成如下形式 (2) (3) (4) 基本步骤可以概括为: (1)利用初始条件,在粗网格上解非线性方程(3),得到粗网格上的近似解。 (2)在细网格上解线性系统(4),求出细网格点(yj,tm)处的数值解。 利用截断技术和逆估计可以证明如下误差估计: u,p,ρ∈C3([0,T];C3[a,b]), 且满足条件 Δt=o(H1/4), 则存在一个与H和Δt无关的正常数C,使得 C(Δt2+h2+H7/2)。 注3由于差分格式是非线性的,利用文献[19]中的截断技巧和逆估计可以证明上述结论成立。 在本节中,使用CN-TG-BCFD算法(3)和(4)分别在均匀和非均匀空间网格上进行数值实验。此外,为了检验二重网格方法的有效性,还将其与完全非线性CN-BCFD算法(3)在细网格上的结果进行比较。 本文考虑的非均匀网格是均匀网格添加一个随机扰动后生成的。首先构造一个均匀网格如下: 然后使用Matlab内联代码对网格步长进行随机小扰动如下所示: Hi=H[1+0.01×ε×rand (i)],i=1,…,N-1。 定义非均匀网格点: 且HN=xN+1/2-xN-1/2。 选取初始条件为: 且可得方程的精确解为 (5) 模拟该孤立波在区间t∈[0,12],x∈[-20,50]上的运动。 数值结果与精确解进行比较,结果如表1~4和图1~3所示。 表1和2分别为均匀网格下CN-TG-BCFD方法(3)、方法(4)和完全非线性CN-BCFD方法(3)的误差、阶数和CPU时间,误差和CPU时间的曲线图如图2所示,其中h=H/5,Δt=h。 图1显示了Δt=h=0.1 时应用二重网格法得到的数值解的运动,这与精确解(5)几乎相同。观察结果如下:(1)这两种方法在离散范数中产生相同量级的误差,并且在空间和时间上都具有二收敛性;(2)提出的二重网格方法更有效。例如,当h=0.025时,非线性格式(3)花费268 547 s(约为3 d),而提出的二重网格方法(3)、方法(4)仅花费不到17 min,对于较小的网格步长,差距更加明显。因此,二重网格法是求解非线性SRLW方程的较好方法。 图1 单孤立波数值解的运动(Δt=h=0.1) (这里三角形正弦值为2。Here the tangent of the triangle is 2.) 表1 均匀网格下二重网格方法(3)和(4)的误差和CPU时间 接下来,测试了大小为H′的非均匀网格上的收敛速度和CPU时间。设定随机扰动ε=0.05,h=H′/5和Δt=h/5,误差和CPU时间显示在表3和4中,并绘制在图3中。在非均匀网格上仍然可以观察到空间和时间上的二阶精度。 (这里三角形正弦值为2。 Here the tangent of the triangle is 2.) 表2 均匀网格下非线性格式(3)的误差和CPU时间 表3 非均匀网格下二重网格方法(3)和(4)的误差和CPU时间 表4 非均匀网格下非线性格式(3)的误差和CPU时间 本文主要讨论了对非线性SRLW方程运用Crank-Nicolson二重网格块中心有限差分方法进行数值求解的问题。在空间上,采用了二重网格块中心差分方法进行离散,而对时间上,则采用了Crank-Nicolson方法进行离散。同时,在均匀和非均匀网格上对孤立波问题进行数值模拟,并将结果与完全非线性块中心差分方法的数值结果进行比较。数值实验表明,采用CN-TG-BC方法求解非线性孤立波方程是可行并有效的,并且这种方法与完全非线性差分方法相比更有优势。

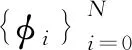







2 全离散二重网格块中心差分格式

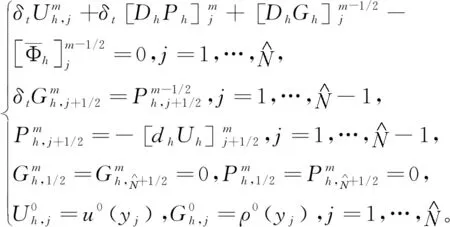
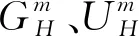

3 收敛性估计及稳定性结果
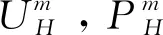
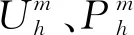
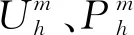
4 数值算例
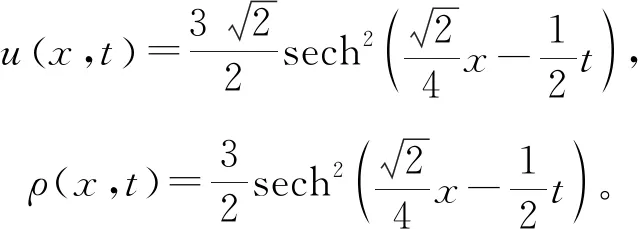


5 结语
