黄丽芹 王在华

(陆军工程大学 基础部，南京 211101)

引言

时滞系统广泛存在于工程技术领域，稳定性是动力学分析与控制设计中的基本问题. 例如，倒立摆作为人体直立姿态平衡的动力学模型是本质不稳定的，必须施加恰当的控制使其稳定在给定的平衡态，当反馈控制环节存在时滞时，就需要研究反馈时滞对倒立摆控制系统平衡点的稳定性. 时滞系统平衡点的(局部)渐近稳定性可由其线性化系统的零解渐近稳定性所确定. 当线性化系统的特征根皆具有负实部时，该系统的平衡点是局部渐近稳定的.由于时滞系统是无穷维系统，有无穷多个特征根，因而时滞系统的稳定性分析是一个不平凡的问题[1, 2].

时滞常常导致系统性能变差，甚至失稳.例如，老年人随着年龄增加，可出现大脑神经、肌肉神经的反应滞后，从而容易导致摔倒. 因此，时滞常被视为不利因素.但人们也可以主动利用时滞，使得时滞有利于控制系统的稳定性.例如，对质量-弹簧-阻尼振动系统施加时滞位移正反馈控制，在一定时滞范围内增加时滞量，可改善系统稳定性，时滞越大，稳定性越好[3]. 因此，在时滞系统稳定性分析中，有必要确定在什么条件下，时滞增加使得稳定性变差，在什么条件下，时滞增加可改善系统的稳定性.

本文仅考察滞后型线性时滞系统，其微分方程可表示为

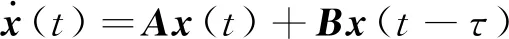
(1)

其中，x∈n,A,B∈n×n，τ>0为时滞. 令x=eλtc为方程(1)的非零解，则常数λ必满足关于c的齐次线性方程组eλt(λI-A-e-λτB)c=0，它有非零解，从而系数行列式必为零，即

|λI-A-e-λτB|=0

(2)

方程(2)称为时滞微分方程(1)的特征方程，其左端函数称为特征函数，记为f(λ)，它的零点称为特征根.时滞微分方程(1)的零解渐近稳定当且仅当其特征方程(2)的所有根都具有负实部.记R(λ)为复数λ的实部，σ为最大实部特征根的实部，即

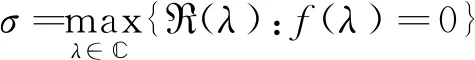
(3)

那么，方程(1)的零解渐近稳定当且仅当σ<0. 当σ<0时，在相同初始条件下，σ越小，时滞系统的非零解收敛到零解的速度越快．因此，对取值连续依赖τ的函数σ=σ(τ)，需要确定σ=σ(τ)在什么情况下递减，在什么情况下递增，在哪些点取极小值或最小值.

为了突出时滞的作用，以下将特征函数f(λ)改记为f(λ,τ). 如果存在τ0>0和实数或复数λ0以及正整数m(≥2)使得

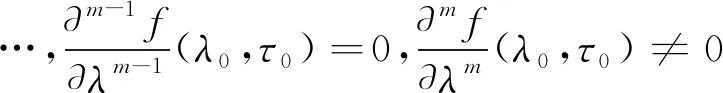
(4)

则称λ0是一个m重特征根. 最近的研究工作表明，可利用参数延拓法得到σ=σ(τ)随时滞变化的曲线，当σ=σ(τ)在给定区间内某点τ0取最小值时，最大实部特征根λ0=σ(τ0)是实数，且为重根. 在τ0附近，m重特征根有m个不同的特征根分支，皆满足λ(τ0)=λ0. 由隐函数存在定理可知，此时重特征根λ不可能展开为τ-τ0的Taylor级数，而需要利用Puiseux级数，m重特征根正好有m个Puiseux级数分别表示m个特征根分支.

Puiseux级数是Taylor级数的推广. 一般地，将一个函数g(x)展开为x=x0处的Puiseux级数，就是要寻找ξ和系数c0,c1,c2,…，使得如下等式成立

(5)

当ξ=1时，Puiseux级数退化为Taylor级数，各系数ck与导数有关系式ck=g(k)(x0)/k!. Puiseux级数中的ξ通常是分数，因而又被称为分数幂级数，没有类似Taylor级数情形的简单公式来计算各系数，待定系数法是常用计算方法. 利用数学通用软件Maple的集成命令，可完成Puiseux级数的常规计算.

采用Puiseux级数求时滞系统m重特征根的各个分支时，首先将特征函数f(λ,τ)近似表示为(λ0,τ0)处的某个阶次的Taylor展开式，得到一个多项式方程，再将Puiseux级数展开式代入此多项式方程，比较同次幂系数，即可依次求得各系数ck. 利用Puiseux级数，便可确定在一定条件下，σ=σ(τ0)在给定的时滞范围内取最小值[4]. 实际上，Puiseux级数在多项式方程和时滞系统稳定性分析中已有许多应用[5]. 例如，Lloyd讨论了机械臂运动学的代数结构，运用Puiseux级数展开，证实了非冗余串行机器人的平滑空间路径总是可以在具有有限重根运动奇点附近平滑地重新参数化[6]；冯二宝在其博士论文中详细讨论了具有有限精度或者数据受到小扰动情况下多项式方程组的交点、拐点、奇异点的数值计算方法，其中包括Puiseux级数展开的数值算法[7]；Chen等人提出用Puiseux级数研究时滞系统特征根在临界虚根附近的渐近行为[8]；Li等人利用Puiseux级数提出一种新的扫频方法研究时滞系统的稳定性[9]；蔡迢阳在其博士论文中研究线性时不变含比例时滞系统中多重纯虚特征根的渐近行为对稳定性的影响时，利用不同根轨迹的Puiseux级数展开[10]来进行稳定性分析[11]. 有关Puiseux级数的进一步介绍与应用可参考文献[12].

由于Puiseux级数在标准的数学课程中没有介绍，因而不被广大科技工作者所熟悉，在实际应用中可能造成误解或误用. 本文首先指出，在时滞系统重特征根分析中，如果将式(5)中的ξ也当作待定常数，则有可能得到相互矛盾的结论而无法求得重特征根的Puiseux级数中的系数. 进而解释了矛盾现象的原因. 最后讨论如何正确运用待定系数法求得Puiseux级数.

1 求多项式方程在重根附近的Puiseux级数的待定系数法

Puiseux级数的作用是确定由多项式方程确定的隐函数在重根附近的近似显式函数关系. 以二元多项式为例，假设多项式方程为

A0(x)yn+A1(x)yn-1+A2(x)yn-2+

…+An-1(x)y1+An(x)y0=0

(6)

其中各系数Ai(x)都是x的多项式，最低次方为ui，即Ai(x)=αixui+h.o.t，其中h.o.t表示关于x的高次项. 假设由此确定的函数在x=x0:=0处有一个重根y=y0:=0，那么在x=x0附近，Puiseux级数的每一个分支具有形式

y=c1xξ+c2x2ξ+c3x3ξ+c4x4ξ+h.o.t

(7)

在重根的一个小邻域附近，可假设x的绝对值是小量，次数越高的项对上式左端数值的影响越小. 待定系数法就是要选取恰当的ξ值，通过由低向高依次消去各低次项而求得各系数ci的值. 为此，将式(7)代入式(6)并加以整理，只保留各个最低次方项的式(6)化为

αnxun+nξ+…+αn-1xun-1+(n-1)ξ+…+

α1xu1+ξ+…+α0xu0+…=0

(8)

其中的省略号皆表示h.o.t. 由此可知，消去最低次项就是要求最低次方min{un+nξ,un-1+(n-1)ξ,…,u1+ξ,u0}在式(8)中出现两次. 例如，对多项式方程

y3+(2+3x)y2+(4x2)y+5x3=0

再由消去次最低次方项等还可确定其他系数c2,c3,….这就是由多项式方程利用待定系数法求Puiseux级数的基本思路和步骤.

2 时滞系统在重根附近Puiseux级数系数计算中的矛盾现象及产生原因

对时滞微分方程，它的特征方程f(λ,τ)=0是含有指数函数的超越方程. 假设在τ=τ0时，特征方程有一个二重根λ=λ0，为了求得重特征根的显式表达式，需要先将特征函数在重根附近用Taylor展开式作近似替代. 为此，令L=λ-λ0,T=τ-τ0, 那么，在τ=τ0附近，f(λ,τ)可用一个p(≥2)阶Taylor展开式来代替. 在一些问题中，p=2即可. 为避免重复表述，下面取p=3，则特征方程f(λ,τ)=0可化为如下近似形式

aL3+bL2T+cLT2+dT3+eL2+fLT+

gT2+hT+h.o.t=0

(9)

这里，在二重根情形下，常数项f(λ0,τ0)=0以及关于λ的一阶导数fλ(λ0,τ0)=0，而关于λ的二阶导数fλλ(λ0,τ0)≠0，从而等式(9)左边不含常数项和L的一次方项，但一定有L的二次方项，其系数e≠0.但是，沿着上一节介绍的针对多项式待定系数法求解思路，可能出现矛盾的结论而无法确定二重根附近的Puiseux级数的系数.

例1考虑某时滞系统的特征函数f(λ,τ)=e-3λτ-3e-2λτ+3e-λτ+λ4+2λ2，当τ0=2π时，λ0=i是一个二重根，满足条件

f(i,2π)=0,fλ(i,2π)=0

其中i2=-1. 另外，直接计算可知此特征函数f(λ,τ)还满足

fτ(i,2π)=0,fττ(i,2π)=0,fλτ(i,2π)=0

(10)

于是二阶Taylor展开式只有一个平方项，无法确定特征根与时滞的关系. 利用三阶Taylor展开式，重根附近的特征方程可近似表示为如下形式(按L的升幂顺序排列)

(iT3)L0+(6πT2)L-(4+12π2iT)L2+

4(-2π3+i)L3+h.o.t=0

(11)

上式各系数关于T的最低次幂分别是3,2,0,0．L=λ-i,T=τ-2π.在(λ,τ)=(i,2π)附近，假设特征根的Puiseux级数为

L=c1Tξ+c2T2ξ+c3T3ξ+c4T4ξ+h.o.t

(12)

将式(12)代入式(11)后化为只有T的表达式，0+3ξ,0+2ξ,2+ξ,3+0是各项中所有可能的最低次数. 由于3ξ≥2ξ，所以所有可能的最低次数是2ξ,2+ξ,3. 由上一节讨论可知，此时必有2ξ=3，即ξ=3/2，且展开式(11)化为

(13)

这表明，采用针对多项式方程提出的求Puiseux级数的标准待定系数法在这里失效了，我们无法用待定系数法确定相应的时滞系统的重特征根的Puiseux级数展开式(12)的高次项.

上述求解过程失效的根本原因是忽略了该特征函数由于满足式(10)而具有的固有特点，即

h=fτ(i,2π)=0，g=fττ(i,2π)/2!=0，

f=fλτ(i,2π)=0

也就是说，Taylor展开式(11)中不显含T,T2,LT的系项. 由下列引理1可知，具有这几个特点的时滞系统都会出现这样的矛盾现象.

引理1设τ=τ0时，时滞系统特征函数f(λ,τ)有二重根λ=λ0. 如果

f=fλτ(λ0,τ0)=0

并且

则沿用上述做法求Puiseux级数会导致错误结论.

事实上，f(λ,τ)的三阶Taylor展开式简化为f(λ,τ)=aL3+(e+bT)L2+cT2L+dT3L0+h.o.t，其中由二重根的假设有e≠0. 假设其Puiseux级数如式(12)，则如前面分析的那样，必有ξ=3/2.故

于是，为了消除最低次项，就得到如下矛盾结论：

类似地，对于二重根处更高次偏导数项等于0，给出另一个充分条件，即为引理2. 为说明方便，下面取p=5，则特征方程f(λ,τ)=0可化为如下近似形式：

pL5+qL4T+rL3T2+sL2T3+tLT4+uT5+

AL4+BL3T+DL2T2+ELT3+FT4+

aL3+bL2T+cLT2+dT3+eL2+fLT+

gT2+hT+h.o.t=0

(14)

引理2设τ=τ0时，时滞系统特征函数f(λ,τ)有二重根λ=λ0. 如果

且

则沿用上述做法求Puiseux级数会导致错误的结论.

事实上，此时特征函数的五阶Taylor展开式简化为

f(λ,τ)=(a+BT+rT2)L3+

(e+bT+DT2+sT3)L2+(ET3+tT4)L+

uT5L0+h.o.t

(15)

其中各系数关于T的最低次幂分别是0,0,3,5. 利用待定系数法，将式(12)代入式(15)后化为只有T的表达式，0+3ξ,0+2ξ,3+ξ,5+0是各项中可能的最低次数. 由于3ξ≥2ξ，所以可能的最低次数是2ξ,3+ξ,5. 由上一节类似讨论可知，此时必有2ξ=5，即ξ=5/2，且展开式(15)化为

于是，为了消除最低次项，就得到如下矛盾结论：

实际上，上述矛盾现象在时滞系统重特征根的Puiseux级数计算中普遍存在. 只要f(λ,τ)关于τ的某阶导数在重根处等于零，则在用待定系数法直接由显式Taylor展开式求Puiseux级数的近似表达式时，就容易忽视T的某些整数次方项系数等于零的事实，从而出现与上述情况类似的矛盾现象.

例2设特征函数f(λ,τ)在τ0处有三重根λ0，即fλ(λ0,τ0)=fλλ(λ0,τ0)=0,fλλλ(λ0,τ0)≠0，且部分偏导数的值满足下面的条件：

fτ(λ0,τ0)=0,fλτ(λ0,τ0)=0

以及

fττ(λ0,τ0)≠0,fλλτ(λ0,τ0)≠0

也就是e=0,f=0,h=0,a≠0,g≠0,b≠0，则对于上述类型的的特征函数，按照例1中确定Puiseux级数最低次方项的做法会导致矛盾结论.

事实上，此时在重根处的三阶Taylor展开式可化为

f(λ,τ)=aL3+(bT)L2+(cT2)L+

(gT2+dT3)L0+h.o.t

(16)

按照L降幂排列，各系数关于T的最低次幂分别是0,1,2,2. 利用待定系数法，假设三重特征根λ0在τ0附近的Puiseux级数仍然为式(12)，将式(12)代入式(16)，最低次幂可能的次数为0+3ξ,1+2ξ,2+ξ,2. 经过比较可知，为了消去最低次方项中的两项，只可能是3ξ=2，即ξ=2/3，此时

令其中的系数等于零即可得到矛盾结论：

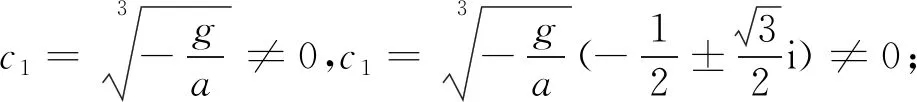
c1=0

类似地，对于三重根处更高次偏导数项等于0，给出另一个充分条件，即为引理3.

引理3设τ=τ0时，时滞系统特征函数f(λ,τ)有三重根λ=λ0. 如果

fτ(λ0,τ0)=fττ(λ0,τ0)=fτττ(λ0,τ0)=0,

fλτ(λ0,τ0)=fλττ(λ0,τ0)=fλλτ(λ0,τ0)=0

且

fττττ(λ0,τ0)≠0,fλτττ(λ0,τ0)≠0

也就是e=0,f=0,c=0,b=0,h=0,g=0,d=0,a≠0,F≠0,E≠0，则对于上述类型的的特征函数，按照例2中确定Puiseux级数最低次方项的做法会导致矛盾结论.

这是因为，此时在重根处的五阶Taylor展开式可化为

f(λ,τ)=(a+BT+rT2)L3+

(DT2+sT3)L2+(ET3+tT4)L+

(FT4+uT5)L0+h.o.t

(17)

按照L降幂排列，各系数关于T的最低次幂分别是0,2,3,4. 利用待定系数法，假设三重特征根λ0在τ0附近的Puiseux级数仍然为式(12)，将式(12)代入式(17)，最低次幂只可能是次数为0+3ξ,2+2ξ,3+ξ,4. 经过比较分析可知，为了消去最低次方项中的两项，和前面的分析类似，为了消去最低次方项中的两项，只可能是3ξ=4，即ξ=4/3，此时

令其中的系数等于零即可得到矛盾结论：

c1=0

定理1设有不可约正整数n>1和m>1，使得在τ0处，时滞方程有m重特征根λ0，满足条件

fλ(λ0,τ0)=fλλ(λ0,τ0)=fλλλ(λ0,τ0)=…

=fλm-1(λ0,τ0)=0,fλm(λ0,τ0)≠0

fτ(λ0,τ0)=fττ(λ0,τ0)=fτττ(λ0,τ0)=…

=fτn-1(λ0,τ0)=0,fτn(λ0,τ0)≠0

其中fτn-1(λ0,τ0),fτn(λ0,τ0)分别表示对τ的n-1阶偏导数与n阶偏导数. 如果存在正整数u,p,v,q满足1≤u≤m，1≤p≤n，v

fλuτ(λ0,τ0)=fλuτ2(λ0,τ0)=fλuτ3(λ0,τ0)=…

=fλuτp-1(λ0,τ0)=0

fλτp(λ0,τ0)=fλ2τp(λ0,τ0)=fλ3τp(λ0,τ0)=…

=fλu-1τp(λ0,τ0)=0,

且满足不等式(u-v)n+(p+q)m

fλu-vτp+q(λ0,τ0)=0,fλuτp(λ0,τ0)≠0

其中pm+un=mn+1，则沿用前面的方法确定Puiseux级数最低次方项的做法会导致矛盾结论.

事实上，f(λ,τ)的m阶Taylor展开式按L的降序排列可记为

f(λ,τ)=A0(T)Lm+A1(T)Lm-1+

A2(T)Lm-2+…+Am-1(T)L+Am(T)L0+

h.o.t

f(λ,τ)=(α+…)Lm+…+

h.o.t

其中括号内的省略号表示关于T的高次方项，且省略号中关于T的次数至少是一次. 上式中为了消去最低次方项中的两项，只可能是mξ=n，故ξ=n/m. 又由上述定理条件知f(λ,τ)可化简为

由上式可知，混合偏导数项最低次为含有系数fλuτp(λ0,τ0)的项，此时

3 待定系数法的正确应用

为了避免上一节讨论的矛盾现象，在求重根附近的Puiseux级数时，需要保留除了重根条件之外的其余所有偏导数对应的项.例如，设在τ=τ0处有二重根λ=λ0，如果利用特征函数f(λ,τ)在(λ0,τ0)处的三阶Taylor展开式来近似替代f(λ,τ). 将二重根时的三阶Taylor展开式(9)按L升幂排列表示为

(dT3+gT2+hT)L0+(fT+cT2)L+

(e+bT)L2+aL3+h.o.t=0

(18)

假设Puiseux级数为

L=c1Tξ+c2T2ξ+c3T3ξ+c4T4ξ+c5T5ξ+

c6T6ξ+h.o.t

(19)

那么，式(18)可变为

为了消去最低次方项，选择ξ使得min (1,1+ξ,2ξ,3ξ)=min (1,2ξ)出现两次，从而有2ξ=1，即ξ=1/2. 依次消去最低次方项T,T3/2,T2,T5/2可得

(20)

由于e≠0，所以由第一个等式可求得

进而依次求得其他各系数.

再由式(20)的第五个等式得到2ec3c4+cc3=0. 由于c3≠0，所以

从而Puiseux级数的范式为

h.o.t

(21)

这样，上述矛盾现象得以避免.但要注意的是，式(21)第二项是T2项，不是T2(3/2)=T3项.

对于二重根的另一个充分条件引理2，类似于例1的讨论得到Puiseux级数的范式为

当λ0是三重根时，类似于前面的做法，将三重根时的三阶Taylor展开式(9)按L升幂排列表示为

(dT3+gT2+hT)L0+(fT+cT2)L+

bTL2+aL3+h.o.t=0

(22)

将式(19)代入式(22)可变为

(23)

由方程组(23)得到

即得Puiseux级数的范式为

或

对于三重根的另一个充分条件引理3，可以类似例2的讨论得到Puiseux级数的范式为

或

一般地，对由时滞系统的特征方程定义的隐函数，在求m重根附近特征根各个分支的Puiseux级数表达式时，如果不限定最低次方项不等于零，可直接将Puiseux展开式各指数幂中的ξ取为ξ=1/m. 对于这个问题更详细的介绍与讨论可参考文献[12].

4 结论

特征根依赖参数的显式表达式对时滞动力系统的稳定性分析具有重要作用，在重根处附近，可采用Puiseux级数展开求得特征根的近似表达式. 和由多项式直接求重根附近的Puiseux级数不同，时滞系统的特征函数是含指数函数的超越函数，需要先将特征函数展开为重根附近的Taylor级数形式，再由Taylor展开式利用待定系数法求Puiseux级数. 本文的价值是发现了利用待定系数法求时滞系统Puiseux级数展开式时出现的矛盾现象，并给出了产生矛盾的原因以及充分条件，最后归纳出满足一定条件的Puiseux级数展开式的范式，为进一步应用提供理论支持.