陈 卫，杨健生，韦冬炎，谌亚菁，彭林欣,2,3

(1.广西大学 土木建筑工程学院，南宁 530004;2.广西大学 广西防灾减灾与工程安全重点实验室，南宁 530004;3.广西大学 工程防灾与结构安全教育部重点实验室，南宁 530004)

壳作为一种重要的结构元件被广泛应用于土木、航天、机械以及船舶等实际工程中。壳体理论经过多年推动发展，已日趋完善。对于特定的壳结构形式解析解也相继涌现。例如圆柱壳弯曲[1-3]、自由振动精确解[4-6]，双曲扁壳弯曲[7]及自由振动[8]的精确解等。然而，由于壳结构形状的多变性，求解壳结构问题的解析解复杂程度很高，手工计算极难完成，因此其相关问题的数值求解显得尤为重要。这些数值方法包括有限单元法[9](finite element method,FEM)，边界元法[10-11](boundary element method,BEM)，等几何分析[12-13](isogeometric analysis,IGA)，小波伽辽金法[14](wavelet Galerkin method,WGM)等。

无网格法作为一种新兴的数值方法，不依赖于网格和单元。基于移动小二乘法构造的高阶连续形函数，能够很好地逼近各类形状壳，而且对薄板壳结构存在的剪切及薄膜锁死现象，只需提高形函数的阶数，就可以完全避免。另外无网格较易实现自适应分析，且在解决超大变形、裂纹扩展及高速冲击等问题上具有一定的优势。在国外，1996年，Krysl等[15]率先将移动最小二乘法近似的无网格法应用到薄壳结构中，采用拉格朗日处理本质边界条件，分析了薄壳的弯曲问题。Noguchi等[16]在Krysl等的基础上结合一阶剪切变形理论，采用罚函数法处理本质边界条件，运用无网格伽辽金法分析了厚壳弯曲问题。Li等[17]采用再生核粒子(reproducing kernel particle method，RKPM)近似的无网格法研究薄壳大变形问题。Liu等[18-19]根据Simo等[20]提出的几何精确壳理论及基尔霍夫假设，采用基于移动最小二乘近似的无网格法分别研究了薄壳的弯曲及振动问题。Kim等[21]采用再生核粒子近似的无网格法分析了壳结构设计灵敏度问题。Chen等[22]采用基于再生核粒子近似的无网格法，运用稳定节点积分，分析了壳结构弯曲问题。Sayakoummane等[23]采用径向基函数(radial basis function，RBF)近似的无网格法分析了壳结构的弯曲问题。Jarak等[24-25]利用无网格局部彼得洛夫-伽辽金法(meshless local Petrov-Galerkin，MLPG)研究了壳的线性弯曲问题。Costa等[26]采用基于再生核粒子近似的无网格法分析壳的弯曲问题，并讨论了拉格朗日、罚函数及Nitsche’s法三种处理本质边界方式的影响。在国内，李迪等[27-28]采用Petrov-Galerkin无网格法研究了壳结构的弹塑性大变形弯曲，利用了罚函数处理本质边界条件。叶翔[29]、王砚[30]与陈靠伟[31]采用基于圆柱壳基本理论与移动最小二乘近似的无网格法研究了圆柱壳振动特性，同样采用罚函数法处理本质边界条件。然而，罚函数[32]在施加本质边界时，存在罚系数不易确定及系统矩阵对角元素变化等缺点，需要不断尝试才能得到精确值。本文将引入完全转化法处理刚度、质量矩阵，便可直接施加本质边界条件，容易实现且精度高。

综上可知，采用无网格法分析任意壳的弯曲问题在国内并不多见，且分析任意壳的自由振动问题在国内外未见相关报道。本文利用无网格法的优点，基于移动最小二乘近似[33]和一阶剪切变形理论[34]，分析任意壳的线性弯曲及自由振动问题。文末选用几个不同形状壳的算例，计算其弯曲或自振频率，并与有限元或理论解进行对比分析，以此来验证该方法在计算任意壳的线性弯曲及自振频率的有效性及合理性。

1 任意壳的无网格基本方程

1.1 移动最小二乘法

函数U(x)在区域Ω(x)内的近似函数为

(1)

式中：pi(x)为矢量基函数；bi(x)为相应系数；m为基函数个数。基函数通常使用多项式，如二维二次基(m=6)，pT(x,y)=[1,x,y,x2,xy,y2]。

根据加权移动最小二乘法确定式(1)中bi(x)，即要求各点处误差加权平方和L2模取最小值

(2)

式中：ω(x-xI)为权函数；n为区域Ωx中权函数大于零的节点数；UI为节点参数。本文权函数取

(3)

令L取最小值，并求偏导，最终可得U(x)的近似函数为

NI(x)=pT(x)A-1(x)BI(x)

(4)

NI(x)=pT(x)A-1(x)ω(x-xI)p(xI)

(5)

1.2 几何模型

如图1所示X=(x,y,z)是在笛卡尔坐标系中的位置矢量，r=(r1,r2,r3)是转换坐标系中的位置矢量。ei是笛卡尔坐标系中正交单位矢量，Vi是壳中面某一点的正交单位矢量。根据Mindlin板壳理论，壳上任意一点的位置矢量可用表示为

图1 板壳几何模型及映射技术Fig.1 Geometric model of shell and mapping technique

(6)

式中：Xmid为壳中面的点在笛卡尔坐标系中的位置矢量；h为壳厚度(等厚度)；ri为转换坐标(r1，r2为壳中面内的参数，r3为厚度方向的参数)；V3为垂直壳中面的单位法向矢量；V1，V2，V3有如下关系

(7)

同样，壳上任意一点的位移矢量参数可表示为

(8)

式中：umid为壳中面的点在笛卡尔坐标系中的位移(u，v，w)，θ1，θ2分别为绕壳中面正交矢量V1，V2的转角。

1.3 位移场近似

根据式(5)利用移动最小二乘法逼近，则壳上任意一点的位置矢量及位移矢量参数可分别表示为

(9)

(10)

式(10)改写成矩阵形式为

(11)

式中：[uI，vI，wI，θ1I，θ2I]T=UI为壳中面上第I个节点的节点参数；uI，vI，wI为壳中面上I节点沿着笛卡尔坐标系x，y，z三个方向的位移；θ1I，θ2I为壳中面I节点绕I节点正交矢量V1，V2的转角；n为壳中面节点个数。

式(9)的位置矢量对转换坐标系ri的偏导，可得到协变基矢量Gi(i=1,2,3)为

(12)

把式(9)代入式(12)，则有

(13)

其中，基矢量ei(i=1,2,3)在笛卡尔坐标系中是正交的，即eiej=δij，而协变基矢量

Gi·Gj≠δij

(14)

根据对偶关系，则逆变基矢量Gj符合克罗内克性质

(15)

根据式(15)，则可推出逆变基矢量为

(16)

1.4 位移-应变关系

根据协变基矢量及逆变基矢量关系，有应变-关系如下

(17)

应变分量εij可写成矢量形式为

(18)

式中，∂u/∂ri为位移矢量u对转换坐标系ri的偏导，写成矩阵形式为

(19)

(20)

式中，Aij(k)为Ai1或Ai2与单位基矢量ek的点积，Aij可写为

(21)

其中，

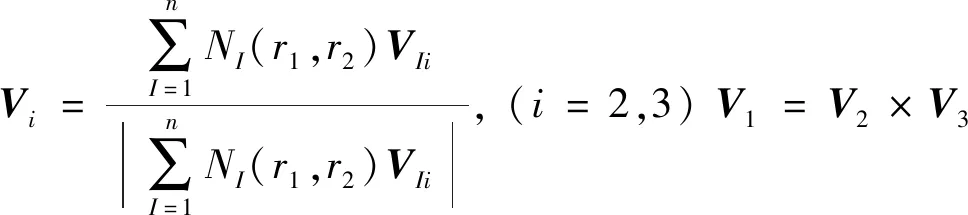
把式(19)、式(20)与代入式(18)可得应变张量εij如下

(22)

应变张量BI改写为矩阵形式有

(23)

式中，Gi(j)为Gi与ej的点积。

1.5 本构关系

对于线弹性材料，本构关系有

σ=Dε

(24)

式中：σ为柯西应力；C为四阶弹性张量；通过正交单位矢量得到如下关系

D=DijklVi⊗Vj⊗Vk⊗Vl

(25)

其中，

式中：Ks为剪切修正因子,Ks=6/5；E为弹性模量；ν为泊松比。

基于协变基矢量及逆变基矢量，弹性张量D也可表示为

D=DijklGi⊗Gj⊗Gk⊗Gl

(26)

其中，

Dijkl=Dmnop(Vm·Gi)(Vn·Gj)(Vo·Gk)(Vp·Gl)

1.6 控制方程

壳在横向荷载作用下的能量泛函为

(27)

式中：ρ为壳的密度；g为重力加速度；q为横向均布荷载(板)；p为集中荷载。

将位移场公式(11)代入式(27)，并结合应变方程式(22)，可得

(28)

其中，

由于本文算例中只考虑重力、集中荷载及板的横向均布荷载，只列出这三种荷载类型。对于壳的法向均布荷载只需把荷载乘以x,y,z三个方向的方向余弦便可得到。x0为集中荷载作用点。

由最小势能原理，泛函的变分ΠB=0，则壳弯曲控制方程为

KU=F

(29)

自由振动时，节点参数uI，vI，wI，θ1I，θ2I都是关于时间t的函数，能量泛函为

(30)

其中，

(31)

式中：“‥”为关于时间t的二阶偏导；ρ为密度。结合应变方程式(22)，可得

(32)

其中，

(33)

根据Hamliton原理，由泛函的变分ΠV=0，则壳自由振动控制方程为

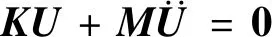
(34)

2 本质边界条件处理

基于MLS的无网格法不满足克罗内克条件，式(29)与式(34)的未知量是节点参数而非真实位移，不能像有限元法那样直接施加本质边界条件。本文采用Chen等[35]提出的完全转换法处理后，可以直接施加本质边界条件。

(35)

其中，

式中，UI为节点参数。式(35)两边同时乘以Λ-1得到

(36)

令T=Λ-1，变换式(36)有

(37)

把式(36)代入式(29)得到

(38)

式(38)两边同时乘以TT得到

(39)

式(39)可改写为

(40)

同样，式(34)可修改为

(41)

通过解如下方程特征值问题，可得到任意壳的自振频率。

(42)

3 算 例

所有算例中影响域均采用方形，定义hr1=dmax×cr1,hr2=dmax×cr2。hr1为影响域r1方向长度，hr2为影响域r2方向长度，cr1为r1方向两个相邻节点的距离，cr2为r2方向两个相邻节点的距离，取dmax=3。采用高斯积分为3×3×2，基函数取m=6。所有模型采用ABAQUS建模时，均采用4节点壳单元(S4R)，结点数均大于1 000。所有算例中，记CCCC为四边固支，SCSC为一邻边固支，另一邻边铰接，SSSS为四边铰接。为了讨论本文方法的收敛性，每个算例中均采用不同均匀布置的离散节点方案进行分析，并将计算结果与精确解或者有限元解进行对比分析。

3.1 平 板

平板是壳结构形式的一种特殊形式。如图2所示，方板尺寸为L=20 m，厚度h=1 m，均布载荷P=1 N/m2，材料参数E=10 000 N/m2，泊松比ν=0.499 99(近似为不可压缩材料)。由于对称性取1/4结构进行分析。讨论节点数布置方案对四边固支及四边简支板挠度的影响，计算结果和精确解[36]的对比曲线如图3所示。从图3可知，对简单的板结构，利用较少的节点(5×5)也能得到很准确的结果，取二次基函数m=6时，不存在体积锁现象。

图2 平板无网格模型Fig.2 Meshfree model of plate

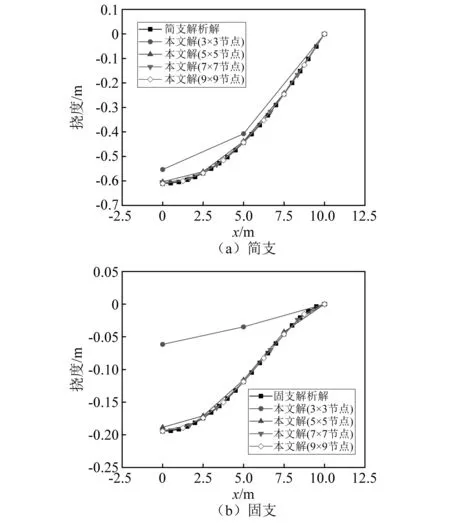
图3 平板沿中心线的垂直位移Fig.3 Vertical displacement of plate along the center line

3.2 圆柱壳

如图4所示，长圆柱壳半径R=5 m，长度L=10.35 m，厚度h=0.094 m，材料的弹性模量E=10.5 MPa，泊松比ν=0.312 5，在圆柱壳中心点受一集中力P=100 N作用。集中力作用点竖向位移的解析解[37]为0.113 9 m，由于对称性取1/8结构进行分析，收敛曲线如图5所示。计算结果表明：随着节点数增多，本文方法能有效地逼近有限元解，体现了本文方法良好的收敛性。

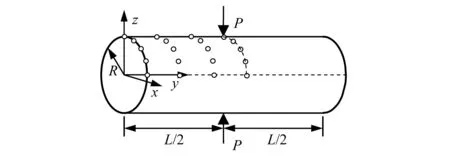
图4 圆柱壳无网格模型Fig.4 Meshfree model of cylindrical shell

图5 圆柱壳沿中心线的垂直位移Fig.5 Vertical displacement of cylindrical shell along the center line

3.3 屋顶壳

3.3.1 屋顶壳弯曲分析

如图6所示，曲边固支的屋顶壳半径R=25 m，弧角度θ=40°，长度L=50 m，厚度h=3 m，材料的弹性模量E=3 MPa，泊松比ν=0.3，密度ρ=9 kg/m3，重力加速度g=10 N/kg。由于对称性取1/4结构进行分析，收敛曲线如图7所示。研究表明，采用15×15节点离散时，本文方法计算结果与有限元解相比均在5%以内，可认为该离散方案使得该算例弯曲分析已收敛。

图6 屋顶壳无网格分析模型Fig.6 Meshfree model of barrel vault roof

图7 屋顶壳沿中心线的垂直位移Fig.7 Vertical displacement of barrel vault roof along the centerline

3.3.2 屋顶壳自振频率分析

屋顶壳的几何尺寸及其他无网格参数如同3.3.1节。取其全结构计算边界条件SSSS、SCSC和CCCC时屋顶壳的自振频率，相关计算结果绘制于图8及表1中。计算结果表明：对于屋顶壳的自振频率分析，本文解的收敛速度快，只需9×9节点方案就可得到与有限元很相近的解(见图8)；采用15×15节点方案时，本文解与有限元解的误差均在1%以内，有效验证本文方法的准确性(见表1)。

图8 屋顶壳SSSS边界下自振频率收敛性分析Fig.8 Convergence analysis of natural frequency of roof shell with SSSS boundary condition

表1 屋顶壳不同边界下前10阶自振频率Tab.1 The first ten natural frequencies of barrel vault with different boundaries condition

3.4 双曲扁壳

3.4.1 双曲扁壳弯曲分析

如图9所示，四边固支(CCCC)的双曲扁壳在中心点受P=4 N的集中力作用，扁壳的长度L=6 m，厚度h=0.2 m，弹性模量E=30 000 N/m2，泊松比ν=0.3。集中荷载处挠度的解析解为0.010 6 m，由于对称性取1/4结构进行分析，收敛曲线如图10和图11所示。研究表明：本文方法在分析双曲扁壳时，除集中荷载处外，只需较少的节点就可以得到较好的计算结果(见图10)；对双曲扁壳弯曲分析，本文方法的收敛性比有限元快(见图11)。

图9 双曲扁壳无网格模型Fig.9 Meshfree model of hyperbolic shallow shell

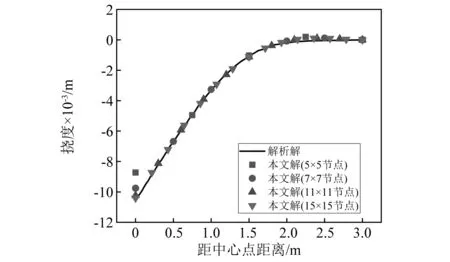
图10 双曲扁壳沿中心线的垂直位移Fig.10 Vertical displacement of hyperbolic shallow shell along the centerline

图11 双曲扁壳中心点垂直位移的收敛性Fig.11 Convergence of the vertical displacement of the center point of a hyperbolic shallow shell

3.4.2 双曲扁壳自振频率分析

双曲扁壳的密度ρ=1 000 kg/m3，几何尺寸及其他参数同3.4.1节，取其全结构进行分析。讨论边界条件为SSSS、SCSC和CCCC时双曲扁壳自振频率，相关计算结果绘制于图12及表2。结果表明，本文方法在分析双曲扁壳自由振动时具有良好的收敛性及较高的精度。

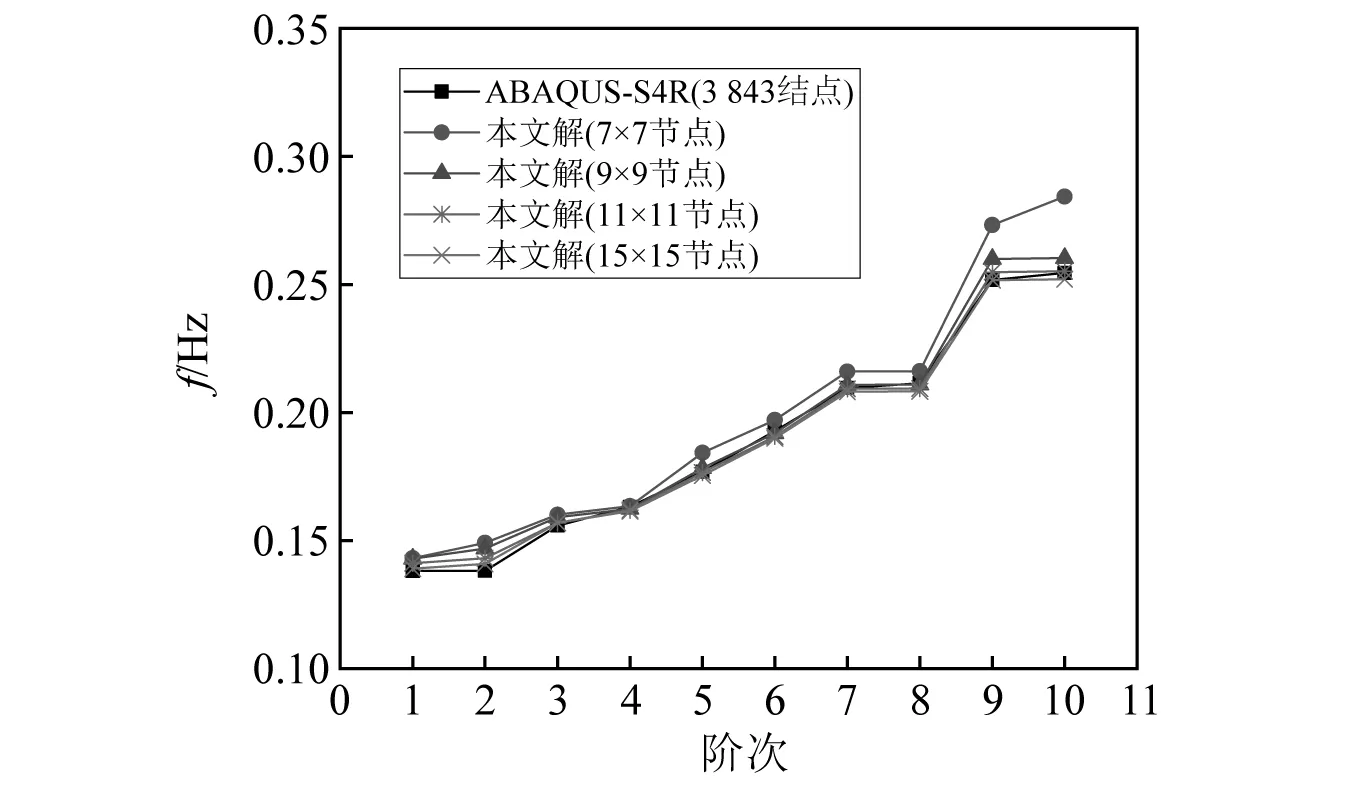
图12 双曲扁壳SSSS边界下自振频率收敛性分析Fig.12 Convergence analysis of natural frequency of hyperbolic shallow shell with SSSS boundary condition

表2 双曲扁壳不同边界下前10阶自振频率Tab.2 The first ten natural frequencies of hyperbolic shallow shell with different boundaries condition

3.5 波纹板自振频率分析

如图13和图14所示，四边固支(CCCC)的余弦波波纹板板长L=1.8 m，W=1.8 m，板厚h=0.018 m，半波长c=0.3 m，弹性模量E=30 GPa，泊松比ν=0.3，密度ρ=7 830 kg/m3，共3个完整波纹。幅值F=0.01时，波纹板在不同节点数离散方案情况下前10阶的自振频率如图15所示。为验证本文方法求解波纹板自振频率的适用性，讨论波纹幅值F从0.01～0.04 m变化时，波纹板的自振频率情况，相关计算结果列于表3。当幅值F=0.04 m时，波纹板自由振动的前3阶模态如图16所示。

图16 波纹板(F=0.04 m)CCCC边界下自由振动前3阶模态Fig.16 The first three modes of free vibration of corrugated plate (F=0.04 m) with four edges clamped (CCCC) boundary condition

表3 余弦波纹板四边固支(CCCC)边界下前10阶自振频率Tab.3 The first ten natural frequencies of corrugated plate with four edges clamped (CCCC) boundary condition

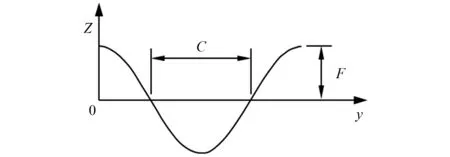
图13 波纹板剖面示意图Fig.13 Schematic diagram of corrugated plate section

图14 波纹板无网格模型Fig.14 Meshfree model of corrugated plate

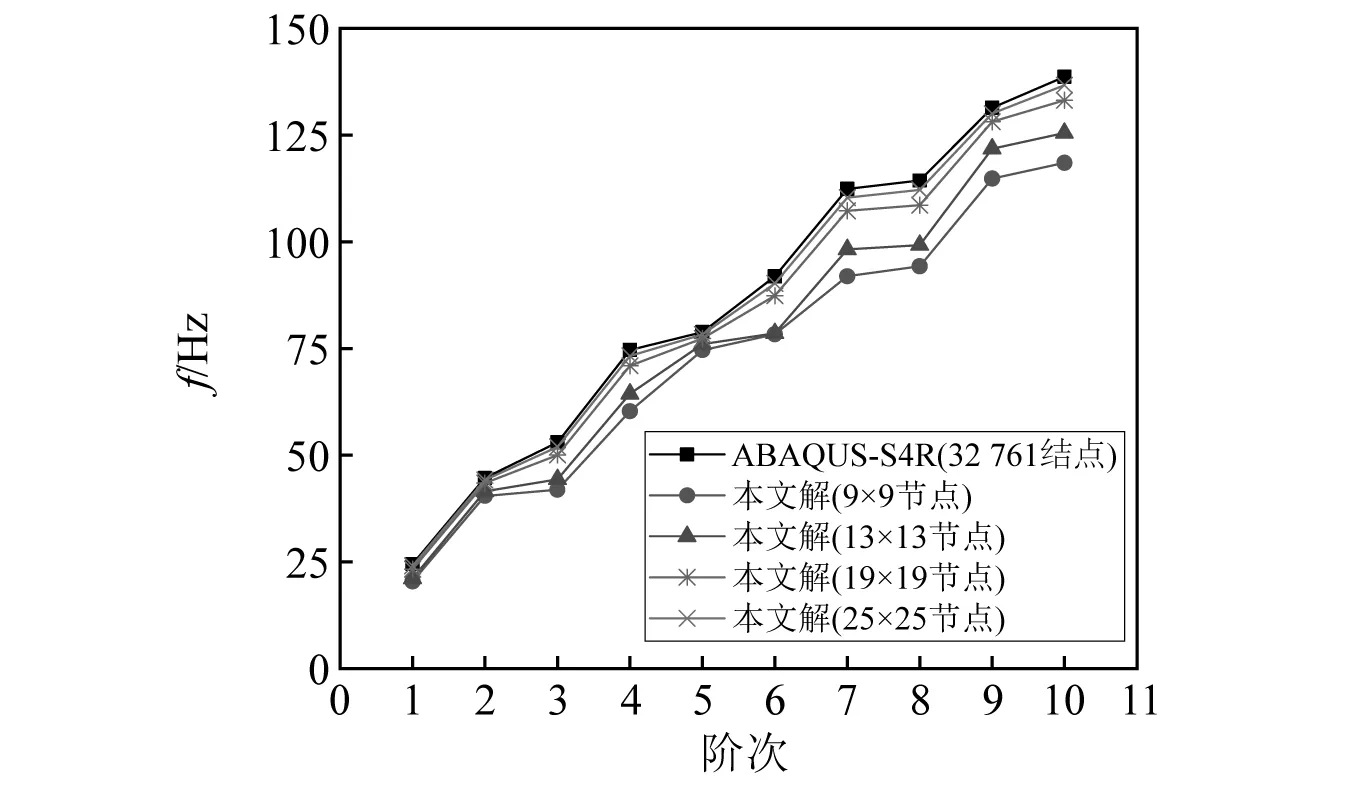
图15 当幅值F=0.01 m时波纹板自振频率收敛性分析Fig.15 Convergence analysis of natural frequency of corrugated plate with amplitude F=0.01 m

研究表明：波纹板因其几何形状比屋顶壳及双曲扁壳复杂，需布置更多的离散节点才能使计算结果收敛(对比图15、图12及图8)；对于幅值F=0.01～0.04 m的波纹板，采用25×25节点离散方案得到的结果与有限元对比，误差均在5%以内。

4 结 论

本文基于移动最小二乘法和一阶剪切变形理论，推导了求解任意壳的无网格列式，采用完全转换法处理边界条件，计算了任意壳的线弹性弯曲及自振频率问题，并与解析解及有限元解对比。结果表明：

(1) 本文方法计算任意壳的线性弯曲及自振频率精度高，随着节点的增加，计算结果数值稳定地趋近解析解或有限元解，表现出良好的收敛性。

(2) 计算所得的弯曲挠度、自振频率与解析解或有限元解很接近，其中自振频率的结果与有限元解之间的误差均在5%以内，验证了该方法的有效性。

(3) 采用基于移动最小二乘近似的无网格法求解任意壳，前处理简单，只需少量的节点信息，就能很好逼近不同形状壳结构形式，且可以有效地避免有限元中复杂的网格划分及网格畸变的影响，在工程实践中具有广阔的应用前景。