盛焕义, 刘 辉, 辛 杰②

(①曲阜师范大学数学科学学院,273165，曲阜市; ②山东农业大学信息科学与工程学院,271018,山东省泰安市)

0 引 言

关于标准拉普拉斯算子的证明已经在很多文献中证明了,例如在文献[3-5,18]中给出了自治随机方程的证明,在文献[1,6,11]中给出了非自治随机方程的证明. 然而对于分数阶拉普拉斯算子的随机方程的吸引子的证明却很少.本文引用文献[16,17]中的 Hindmarsh-Rose 方程并借鉴分数阶随机方程的吸引子的证明文献[15,21],讨论了非自治分数阶随机 Hindmarsh-Rose 方程的随机吸引子的存在性.本文的主要困难在于分数阶拉普拉斯算子的非自治随机方程的解的拉回随机吸收集和渐近紧性的证明,创新点是非线性项f(t,x)是作为一个具体的确定性方程在随机方程中进行研究. 我们改进了文献[21]中的方法,将f(t,x)的确定方程代入整体方程中,并把单一的方程扩展成Hindmarsh-Rose的3个方程组,之后再将它们写成向量形式的方程进行证明计算.

本文将考虑下列非自治非局部分数阶随机 Hindmarsh-Rose 方程在O上的渐近行为[15,16]

(1)

(2)

(3)

具有边界条件

u(t,x)=0,v(t,x)=0,z(t,x)=0,x∈∂O,t>τ

(4)

和初始条件

u(τ,x)=uτ(x),v(τ,x)=vτ(x),z(τ,x)=zτ(x),x∈O,

(5)

其中,t>τ∈,x∈O⊂n(n≤3),算子(-Δ)s称为具有s∈(0,1)的分数阶拉普拉斯算子,O是n上的一个光滑有界域,W是一个在概率空间上的双面实值维纳过程,激励注入电流J为常数,在(1)式和(2)式中的非线性项为

φ(u)=au2-bu3,ψ(u)=α-βu2.

(6)

(7)

除了c(=uR)∈是神经元细胞膜电位的参考值之外,其它所有涉及到的参数d1,d2,d3,a,b,α,β,q,r,J和ε都是常数.

在动力系统(1)～(3)中,变量u(t,x)表示神经元细胞的膜电位,变量v(t,x)表示钠、铁离子通过快速离子通道的转速率并称为尖峰变量,变量z(t,x)表示通过与破裂现象相关的钙等离子的慢通道穿过神经元细胞膜的转速率并称为破裂变量[16,17].

接下来我们给出具有初始-边界条件(4)和(5)的非自治系统(1)～(3)的向量形式

(8)

具有边界条件

g(t,x)=0,x∈∂O,t>τ，

(9)

初始条件为

g(τ,x)=gτ(x),x∈O,

(10)

其中

g(t)=col(u(t,·),v(t,·),z(t,·)),gτ=col(uτ,vτ,zτ),

并且p(t,x)=col(p1(t,x),p2(t,x),p3(t,x)),正矩阵

(11)

通过带有乘性噪声的随机Hindmarsh-Rose方程的初边值问题(1)～(6),给出了Hilbert 空间

F=[L2(O)]3=L2(O,3)和E=[H1(O)]3=H1(O,3).

(12)

是一个局部 Lipschitz 连续映射,λ是一个正的常数. 算子(-Δ)s被称为一个分数阶拉普拉斯算子,其中s∈(0,1),当s=1时,成为了标准拉普拉斯算子.

本文剩余部分安排如下. 第1节回顾了非自治随机动力系统的随机吸引子的存在性的一些基础结论. 第2节利用伽略金方法证明了非自治分数阶随机方程(8)的解的存在性和唯一性,并基于解算子定义了一个连续 cocycle. 第3节得到了大量的解的一致估计,这是证明拉回随机吸收集和渐近紧性所必需的. 最后，第4节证明了调和拉回随机吸引子的存在性.

1 预备知识

本节简要地回顾非自治随机动力系统的一些符号和结论. 假设(Ω,F,) 是一个概率空间,并且(X,d)是一个可分离度量空间. 我们用d(A,B)来表示X中非空子集A和B的Hausdorff半距离.

定义1.1令(Ω,F,,(θt)t∈)是一个度量动力系统,映射Φ:+××Ω×X→X称为在X上覆盖(Ω,F,,(θt)t∈b)的一个连续 cocycle,如果对于所有的τ∈,ω∈Ω和t,s∈+满足以下条件:

(1) Φ(·,τ,·,·):+×Ω×X→X是一个(B(+)×F×B(X),B(X))-可测映射;

(2) Φ(0,τ,·)在X上是恒等的;

(3) Φ(t+s,τ,ω,·)=Φ(t,τ+s,θsω,·)∘Φ(s,τ,ω,·);

(4) Φ(t,τ,ω,·):X→X是连续的.

定义1.2设D为X中的非空子集的一些族的集合,Φ是X上的一个连续 cocycle. 如果对于所有τ∈,ω∈Ω和任何序列tn→∞,xn∈D(τ-tn,θ-tnω)时,序列在X中有一个收敛的子序列,则Φ被称为在X内的D-拉回渐近紧.

定义1.3设D为X中的非空子集的一些族的集合.如果对于任意有界集B∈存在一个有限时间T>0,对于所有的t>T,ω∈Ω使得Φ(t,τ-t,ω,B)⊂K,则称集合K∈D是关于Φ的一个拉回吸收集.

定义1.4设D为X中的非空子集的一些族的集合,并且A={A(τ,ω):τ∈,ω∈Ω}∈D. 则A称为Φ的一个D-拉回吸引子,如果满足下列条件:

(1)A是可测的,并且对于所有τ∈和ω∈Ω,A(τ,ω)是紧的;

(2)A是不变的,即,对于所有τ∈和ω∈Ω 都有

Φ(t,τ,ω,A(τ,ω))=A(τ+t,θtω),t≥0

成立;

(3)A吸引D中的每一个元素,即对于给定的B∈D和τ∈和ω∈Ω都满足

命题1.5设D是X中的非空子集的一些族的闭包集,Φ是X上覆盖(Ω,F,,(θt)t∈)的一个连续 cocycle. 如果Φ是X上的D- 拉回渐近紧并有一个闭的D-拉回吸收集K在D中,则Φ在D中有一个D-拉回吸引子A,这个拉回吸引子A是唯一的并且由下列给出,即对于所有的τ∈和ω∈Ω,

本文用‖·‖和 (·,·)表示L2(n)的范数和内积,Hs(n)的Gagliardo 半范数用来表示. 在这里解释齐次狄利克雷边界条件(9)是当u=0时,u∈nO而不只是u∈∂O. 这种解释与积分分数阶拉普拉斯算子的非局部性是一致的.在这种解释的基础上,我们引入了空间V={u∈Hs(n):u=0a.e. onnO},并且考虑特征值问题

(-Δ)su=λu,u∈O, 并且当u∈∂O时,u=0.

(13)

(-Δ)s的特征方程将构造本文中问题(8)～(10)的解.

2 余圈(Cocycle)

本节通过方程(8)～(10),并将边界条件(9)替换成在nO上g=0,建立了以下具有s∈(0,1)的由乘性白噪声驱动的非自治分数阶随机 Hindmarsh-Rose 方程并证明了连续 cocycle 的存在性

(14)

具有边界条件

g(t,x)=0,x∈nO,t>τ

(15)

和初始条件

g(τ,x)=gτ(x),x∈O,

(16)

为了方便,我们给出一个确定的正数λ,并且对于所有的t∈,x∈O和g∈,令

f(t,x,g)=λg+F(t,x,g).

(17)

注意,给定的t,g∈,f(t,x,g):O→只是定义在空间O上. 但是对于所有的x∈nO,可以通过设f(t,x,g)=0来将f(t,·,g)推广到整个空间n上. 这样的一个推广经常在本文中使用. 换言之,任何定义在空间O上的函数都可以等价于对空间n上的平凡扩张.

根据(17)式,方程(14)～(16)可以写成

(18)

具有边界条件

g(t,x)=0,x∈nO,t>τ

(19)

和初始条件

g(τ,x)=gτ(x),x∈O.

(20)

θtω(·)=ω(·+t)-ω(t),t∈,ω∈Ω.

考虑一维随机方程

dy+ydt=dW.

由文献[2]知,该方程由唯一的稳定解y(t)=z(θtω),其中z:Ω→是由z(ω)=-eτω(τ)dτ(ω∈Ω)给出的随机变量. 此外,存在一个全测度Ω0的θt-不变集,使得z(θtω)对每一个ω∈Ω0都是路径连续的,并有

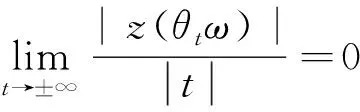
(21)

为方便起见,后续将不再区分 Ω0和 Ω,而是对 Ω0和Ω使用相同的符号Ω.

为达到目的,需要将随机方程(14)转换成由ω∈Ω 参数化的确定性方程. 为此引入了新的变量Q(t,ω)=e-εz(θtω),令

G=G(t,τ,ω,Gτ)=e-εz(θtω)g(t,τ,ω,gτ)，

(22)

并且Gτ=e-εz(θtω)gτ,其中τ∈是一个确定的初始时间,t≥τ,ω∈Ω,Gτ∈L2(O),并且g=g(t,τ,ω,gτ)是(18)～(20)的解. 于是得到,对于t>τ,

(23)

具有边界条件

G(t,x)=0,x∈nO,t>τ,

(24)

初始条件

G(τ,x)=Gτ(x),x∈O.

(25)

将首先证明方程(23)～(25)的解的存在性和唯一性,然后通过变换(22)得到方程(14)～(16)的解. 回忆V是由V={g∈Hs(n):g=0 a.e. onnO}所定义的.V的对偶空间被定义为V*.为了证明解的存在性,也需要空间H={g∈L2(n):g=0 a.e. onnO}.注意空间H的定义符合条件(24)和(25),因为对于x∈nO,通过设g(x)=0可以将一个函数g∈L2(O)看作为空间H的一个元素.

令a:V×V→是双线性形式,对于G1,G2∈V,

(26)

通过使用a的双线性形式,定义了A:V→V*由

(A(G1),G2)(V*,V)=a(G1,G2),对于所有的G1,G2∈V,

(27)

其中(·,·)(V*,V)是V*和V的对偶对.

很明显算子A是单射. 另一方面,由 Riesz 表示定理可知,A也是满射并且逆映射A-1:V*→V是被明确定义的.

定义2.1对于给定的τ∈,ω∈Ω和Gτ∈H,连续函数G(·,τ,ω,Gτ):[τ,∞)→H被称为问题(23)～(25)的解,如果G(τ,τ,ω,Gτ)=Gτ并有

并且对于所有的ξ∈V∩L2(n),解G在(τ,∞)区间内满足

(28)

下面我们准备证明方程(23)～(25)的解的存在性和唯一性.

定理2.2对于所有的τ∈,ω∈Ω和Gτ∈H,问题(23)～(25)在定义 2.1 的意义下有唯一的解G(t,τ,ω,Gτ),在空间H中,解在ω下是(F,B(H))-可测的并且在初始条件Gτ下是连续的. 然而,解G对于几乎所有的t≥τ满足下列能量方程

(29)

证明首先构造有限维系统的一系列近似解,然后得到一致估计,最后得到这些近似解的极限,具体证明过程省略.

接下来将证明方程(23)～(25)在空间H中随机吸引子的存在性. 为此,需要建立下文所介绍的在空间H中的解算子的紧性.

引理2.3给定τ∈,t>τ和ω∈Ω,方程(23)～(25)的解算子G(t,τ,ω,·):H→H是紧的,即对于空间H中所有的有界序列序列在空间H中有一个收敛的子序列.

这说明了存在一个零测度的集合I(I⊂[τ,τ+T])和一个子序列,使得对于所有的r∈[τ,τ+T]I,

(30)

由于t>τ,(τ,t)⊆[τ,τ+T]和I有零测度,存在r0∈(τ,t)I,于是由(30)式得到

(31)

由(31)式和在初始数据下解的连续性,得到

这就推出了该证明.

由方程(23)～(25)的解G和变换(22),得到随机方程(14)～(16)的一个解

g(t,τ,ω,gτ)=eεz(θtω)G(t,τ,ω,Gτ),

并有gτ=eεz(θtω)Gτ. 由引理 2.1 得到当t∈[τ,∞)和Gτ∈H时g(t,τ,ω,gτ)都是连续的. 然而,g(t,τ,·,gτ):Ω→H是可测的. 于是在空间H中定义一个关于方程(14)～(16)的解的一个连续 cocycle. 令Φ:+××Ω×H→H是一个映射,使得对于所有的t∈+,τ∈,ω∈Ω和gτ∈H,

Φ(t,τ,ω,gτ)=g(t+τ,τ,θ-τω,gτ)=eεz(θtω)G(t+τ,τ,θ-τω,Gτ),

(32)

其中Gτ=e-εz(ω)gτ. 回忆一类L2(n)中的有界非空子集,D={D(τ,ω):τ∈,ω∈Ω}是调和的,如果对于所有的c>0,τ∈和ω∈Ω,

其中关于L2(n)中的子集D的符号‖D‖可以理解为在空间L2(n)中的有界非空子集的所有调和族的集合为D,即

D={D={D(τ,ω):τ∈,ω∈Ω}:D在L2(n)中是调和的}.

(33)

在这样的情况下,D-拉回吸引子也可以称作调和吸引子,因为由(33)式给出的D包含L2(n)上的有界非空子集的所有调和族.

现在,假设对于所有的τ∈,

(34)

当推导调和拉回吸收集的存在性时,我们将进一步假设p是调和的,对于所有的c>0,

(35)

很明显,(34)和(35)式并不意味着当t→∞时p在L2(n)内是有界的.

3 方程解的一致估计

本节推导了分数阶随机方程的解的一致估计,这是为了构造关于 cocycle Φ的随机拉回吸收集.

引理3.1在条件(34)下,对于所有的ε0>0,σ∈,τ∈,ω∈Ω和D={D(τ,ω):τ∈,ω∈Ω}∈D,存在T=T(τ,ω,D,σ,ε0)>0使得对于所有的t≥T和0<ε≤ε0,方程(23)～(25)的解G满足

其中eεz(θ-tω)Gτ-t∈D(τ-t,θ-tω)并且β1是不依赖于τ,ω,D和ε的一个正常数.

证明使用能量方程(29)来推导所需的估计. 首先,由 Young 不等式得到,对于(29)式的最后一项

(36)

另一方面,

(37)

由(36)～(37)和(29)式，得

(38)

在上式中用θ-τω代替ω,得

接下来改变变量,得

(39)

现在估计(39)式右边部分的第一项. 注意

由于eεz(θ-tω)Gτ-t∈D(τ-t,θ-tω)和0<ε≤ε0,所以从上式中得

(40)

由(21)式得，存在T1=T1(ω,ε0)>0,使得对于所有的t≥T1,有

(41)

由(40)～(41)式得，对于所有的t≥T1,有

(42)

由于D={D(τ,ω):τ∈,ω∈Ω}是调和的，当t→∞时,有

因此,由(42)式得，存在T2=T2(τ,ω,D,σ,ε0)≥T1使得对于所有的t≥T2,有

(43)

对于(39)式右边部分的第二项,有

(44)

通过(41)式有,对于所有的t≥T1

(45)

注意到,由于(34)式可知上式最后一个积分是收敛的. 通过(44)～(45)式得

(46)

由于(45)式可知上式积分是收敛的. 通过与(46)式相同的论证,也可以得到

(47)

由(39),(43)和(46)～(47)式得,对于所有的t≥T2,

‖G(σ,τ-t,θ-τω,Gτ-t)‖2+

(48)

由(48)式,所需的估计直接得出.

在引理4.1的基础上,我们将在下面阐述方程(23)～(25)的解算子有一个随机拉回吸收集.

引理3.2在条件(35)下,对于每一个ε>0,令Bε={Bε(τ,ω):τ∈,ω∈Ω}是由下列给出的一个随机集

Bε(τ,ω)={G∈H:‖G‖2≤rε(τ,ω)},

其中R=Rε(τ,ω)是一个正整数,形式如下

(49)

其中β1是和引理 3.1 中相同的常数. 于是对于所有的τ∈,ω∈Ω和D={D(τ,ω):τ∈,ω∈Ω}∈D,存在T=T(τ,ω,D,ε)>0,对于所有的t≥T和eεz(θ-tω)Gτ-t∈D(τ-t,θ-tω),使得对于(23)～(25)的解G满足

G(τ,τ-t,θ-τω,Gτ-t)∈Bε(τ,ω).

(50)

另外,随机变量Rε在(49)是调和的,即对于任何c>0,

(51)

证明作为引理3.1中当σ=τ时的特殊情况,直接就得到了(50)式. 现在证明(51)式. 由于(49)式有

(52)

(53)

注意,如果t≥T0和s≤0,于是有t-s≥t≥T0. 因此,对于所有的t≥T0和s≤0从(53)式中得

(54)

(55)

|-2εz(θs-tω)|≤2εc3(t-s).

(56)

由(52)和(54)～(56)式得,对于所有的t≥T0,

因此由(35)式得

这就说明了Rε是调和的,正是(51)式所需要的.

接下来证明方程(23)～(25)的解的渐近紧性.

引理3.3在条件(35)下,当t→∞,eεz(θ-tnω)G0,n∈D(τ-tn,θ-tnω),D={D(τ,ω):τ∈,ω∈Ω}时,方程(23)～(25)的解的序列G(τ,τ-tn,θ-τω,G0,n)在空间H上有一个收敛的子序列.

证明当引理 3.1 中σ=τ-1时,得到了这里存在T=T(τ,ω,D,ε)>0和c=c(τ,ω,ε)>0使得对于所有的t≥T,有

‖G(τ-1,τ-t,θ-τω,G0)‖≤c,

(57)

当eεz(θ-tω)G0∈D(τ-t,θ-tω)时,对于任何的G0∈H都成立. 由于tn→∞,有N=N(τ,ω,D,ε)≥1使得对于所有的n≥N,有tn≥T. 由(57)式,存在对于所有的n≥N,

‖G(τ-1,τ-tn,θ-τω,G0,n)‖≤c.

(58)

由(58)式得,序列G(τ,τ-1,θ-τω,G(τ-1,τ-tn,θ-τω,G0,n))在空间H中是预紧的. 这个序列正是G(τ,τ-tn,θ-τω,G0,n).

4 随机吸引子的存在性

本节证明非自治分数阶随机方程(14)～(16)的调和拉回吸引子的存在性. 基于方程(23)～(25)的解的一致估计,首先证明调和拉回吸收集的存在性和方程(14)～(16)的渐近紧性.

引理4.1在条件(35)下,给定ε>0,τ∈和ω∈Ω,令

Kε(τ,ω)={g∈H:‖g‖2≤e2εz(ω)rε(τ,ω)},

其中Rε(τ,ω)是和(49)式中相同的数，则Kε={Kε(τ,ω):τ∈,ω∈Ω}∈D是cocycle Φ的一个闭的可测拉回吸收集.

证明首先证明Kε吸收集合D中的每一个数D. 由(22)式有

g(τ,τ-t,θ-τω,gτ-t)=eεz(ω)G(τ,τ-t,θ-τω,Gτ-t),

(59)

其中gτ-t=eεz(θ-tω)Gτ-t.如果gτ-t∈D(τ-t,θ-tω),于是由(59)式得eεz(θ-tω)Gτ-t∈D(τ-t,θ-tω),这和引理 3.2 一起表明，存在T=T(τ,ω,D,ε)>0使得对于所有的t≥T,有

G(τ,τ-t,θ-τω,Gτ-t)∈Bε(τ,ω),

(60)

其中Bε(τ,ω)和(50)式中的相同. 由(59)～(60)和(49)～(50)式得,对于所有的t≥T,有

‖g(τ,τ-t,θ-τω,gτ-t)‖2≤e2εz(ω)rε(τ,ω).

(61)

另一方面,由(32)式有

Φ(t,τ-t,θ-tω,gτ-t)=g(τ,τ-t,θ-τω,gτ-t),

(62)

这和(61)式一起说明了对于所有的t≥T,有

Φ(t,τ-t,θ-tω,gτ-t)∈Kε(τ,ω),

并且因此Kε吸收集合D的所有元素.

现在证明Kε是调和的,即Kε∈D. 由(21)和(51)式，对于所有的c>0,有

这表明了Kε∈D. 注意Rε(τ,ω),当ω∈Ω时是可测的,所以Kε(τ,ω)同样也是.

下面将证明Φ的D-拉回渐近紧性.

引理4.2在条件(35)下,对于每一个τ∈,ω∈Ω和D={D(τ,ω):τ∈,ω∈Ω}∈D,当tn→∞和g0,n∈D(τ-tn,θ-tnω)时,序列Φ(tn,τ-tn,θ-tnω,g0,n)在空间H中有一个收敛子序列.

证明由(59)和(62)式得

Φ(tn,τ-tn,θ-tnω,g0,n)=g(τ,τ-tn,θ-τω,g0,n)=

eεz(ω)G(τ,τ-tn,θ-τω,G0,n),

(63)

其中对于所有的n∈,G0,n=e-εz(θ-tnω)g0,n. 由于g0,n∈D(τ-tn,θ-tnω),得

eεz(θ-tnω)G0,n∈D(τ-tn,θ-tnω).

于是由引理 3.3 得到序列G(τ,τ-tn,θ-τω,G0,n)在空间H中有一个收敛子序列,这和(63)式一起得到了该证明.

本节主要的结论是在下面阐述的Φ在空间H中的调和拉回吸引子的存在性.

定理4.3假设条件(35)成立. 于是方程(14)～(16)的 cocycle Φ在空间H中有一个唯一的D-拉回吸引子Aε={Aε(τ,ω):τ∈,ω∈Ω}.

证明D-拉回吸引子Aε的存在性和唯一性可由引理4.1和引理4.2直接得出文献[2,20,21]的结论.