张 亮，张翔宇，王国宏

（1.海军航空大学信息融合研究所，山东烟台 264001；2.中国人民解放军94326部队，山东济南 250000；3.海军航空大学航空电子与指挥系，山东青岛 266041；4.中北大学信息与通信工程学院，山西太原 030023）

1 引言

现代雷达多使用大时宽带宽积信号，以同时获得高距离分辨率和远作用距离，带宽的增大意味着采样频率的提升，提升采样频率利于改善信噪比（Signal to Noise Ratio，SNR），但也给雷达信号处理带来目标距离走动校正难题［1～4］，特别是目标处于高速机动或雷达工作于长时间积累模式时.雷达相参积累中，通常利用Keystone 变换［5］（Keystone Transform，KT）消除目标距离走动.KT 核心思想是构造虚拟慢时间，去除快时间频率与慢时间耦合关系，当目标存在速度模糊时，还需估计模糊数进行相位补偿，上述过程针对目标仅存在径向速度的情况，当目标存在加速度、加加速度等高阶项时，涉及高阶KT［6，7］，核心思想相同.围绕KT 去耦合问题，文献［8］最早提出利用辛格插值实现，但该方法计算复杂度较高.文献［9］提出基于时间尺度（Time-Scaling，TS）的KT 去耦合方法，文中称其为scaling 原理，该方法数值计算中为实现1个快时间频率单元回波去耦合，需要进行2 次chirp 乘积、2 次chirp 卷积，计算量同样较大.针对该问题，文献［10］联合Chirp-Z 变换（Chirp-Z Transform，CZT）和快速傅里叶逆变换（Inverse Fast Fourier Transform，IFFT），提出“CZT+IFFT”去耦合方法，该方法为实现1个快时间频率单元回波去耦合，仅需要2次chirp乘积、1次chirp卷积和1次IFFT，由于1 次chirp 卷积需要进行2 次快速傅里叶变换（Fast Fourier Transform，FFT）和1 次IFFT，因此计算量低于文献［9］方法，但文中仅给出了方法步骤，未提供充足的理论解释和应用条件分析.除上述方法外，还有基于离散傅里叶变换（Discrete Fourier Transform，DFT）和IFFT 的“DFT+IFFT”方法，文献［11］从工程实现的角度论证得出“DFT+IFFT”方法与文献［10］方法实现过程相同.傅里叶变换作为一种经典的积分变换，以其为纽带揭露了自然界除时间外的另一个基本物理量，频率.科恩认为“尺度是一种像频率一样的物理属性”，而链接时间与尺度的纽带为梅林变换（Mellin Transform，MT）的特例尺度变换［12］（Scale Transform，ST）.ST 具备尺度不变性，该特点可用于计算回波快时间频率单元信号尺度版本，实现KT去耦合.

针对上述问题，本文运用时间尺度和尺度估计（Scale-Estimation，SE）两个基本概念，提出3种KT 实现方法，其中，第1 种方法是对现有“CZT+IFFT”方法的修正，另外2 种方法均利用梅林变换实现，区别在于不同的实现思路.

2 Keystone变换

2.1 基本原理

设窄带雷达载频为f0，发射线性调频（Linear Frequency Modulation，LFM）脉冲信号，脉宽Tp、带宽B、调频斜率为ρ=B/Tp，雷达探测范围内1 个点目标向站飞行，初始距离R0、径向速度vt.设目标反射系数为1，雷达接收射频目标回波为：

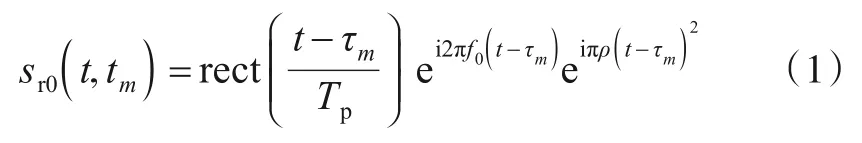
式中：t为快时间，tm=mTr为慢时间，rect[·]为矩形窗函数，m=0，1，2…M-1，M为相参积累个数，Tr为脉冲重复周期，τm=2R(tm)/c为回波时延，R(tm)=R0-vttm为目标与雷达径向距离函数，c为光速.回波下变频得到：

沿快时间进行脉冲压缩，得到：

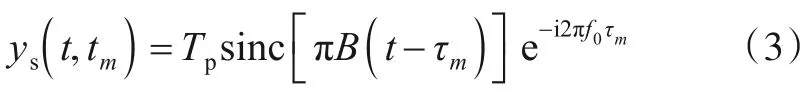
式中：sinc[·]为未归一化的辛格函数.当τm大于雷达1个距离单元对应时延，目标将出现距离走动.为校正距离走动，对脉压后回波沿快时间做傅里叶变换，得到：

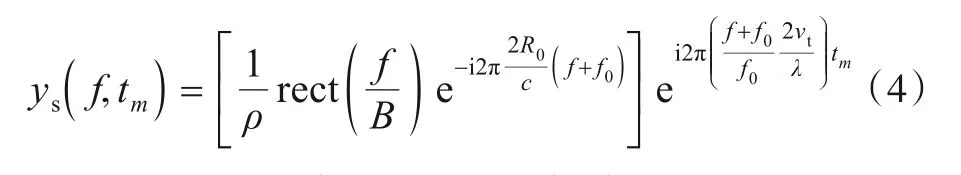
式中：f为快时间频率，与慢时间耦合.构造虚拟慢时间［8～10］，即tom=，带入式（4）：

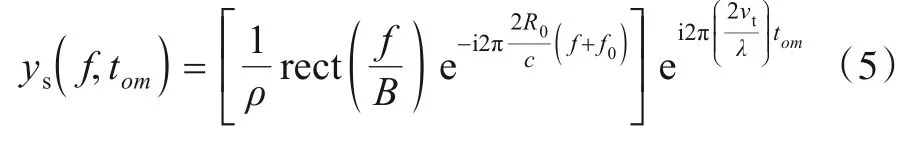
沿快时间频率做逆傅里叶变换，得到：

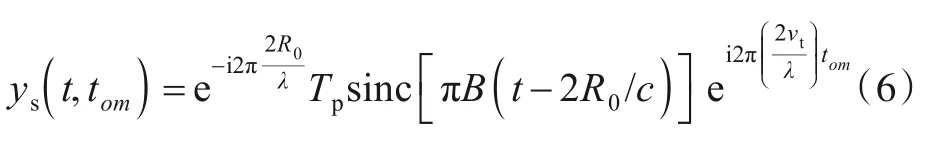
对比式（3）可知，目标距离走动被校正，沿tom做FFT可实现相参积累，上述过程适用目标径向速度不模糊情况，当目标存在速度模糊时，还需对式（4）补偿模糊数，再构造虚拟慢时间去耦合.

2.2 典型实现方法

现有KT 实现方法中，“CZT+IFFT”方法计算量最低.该方法最早由文献［10］提出，文中给出了操作步骤，但未提供充足的理论解释.设离散序列x(n)长度为N，n=0，1，2，…，N-1，其CZT为：

式中：k=0，1，2，…，K-1，K为Z 平面频谱采样点数，A为起始抽样点，W为一个与伸展率和抽样点角度差有关的复标量.“CZT+IFFT”方法要求K=N、A=1、W=exp(-i2πγ/N)，γ为CZT比例系数，式（7）可简化为：

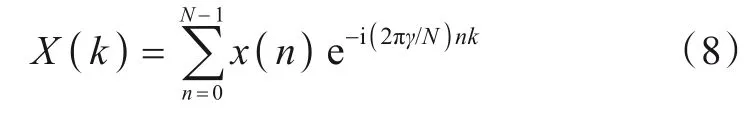
“CZT+IFFT”方法中的IFFT为IDFT快速算法，计算式（8）的IDFT，得到：

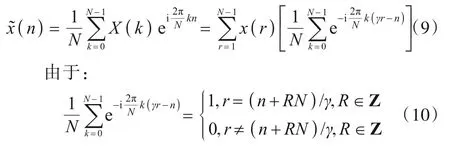
得到：

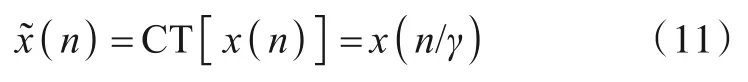
式（12）即为“CZT+IFFT”方法基本原理.该方法在数值计算中并不完美，因为CZT 是一种特殊的Z 变换，式（8）可理解为计算x(n)在单位圆上的N点频谱采样值，间隔为2πγ/N.当γ＜1 时，采样区间位于单位圆内，如果式（12）中的频点(2vt/λ)·(f+f0)/f0位于采样区间外，计算CZT会导致频点丢失，后续的IFFT自然也没有意义；当γ＞1 时，采样区间超出单位圆，出现了频率混叠.为避免频率混叠应调整Z平面采样点数，取：

式中：fix[·]表示向零取整，然后在X(k)后补零，补零长度为N-K，再计算IFFT，本文将其命名为修正的“CZT+IFFT”方法.需要注意的是，该方法同样无法解决可能的频点丢失问题，由于减少了Z 平面采样点数（γ＞1），受噪声影响会相应增大.另外，至于何种情况下会发生频点丢失问题，具体与目标不模糊多普勒频率和(f+f0)/f0数值有关.由于目标不模糊多普勒频率通常是未知的，因此(f+f0)/f0数值越小，CZT 采样区间也越小，发生频点丢失的概率也越大.

3 Keystone变换实现思路

时间尺度（TS）与尺度估计（SE）是关于尺度的2 个基本概念，文献［9］最早将TS引入KT（文中称其为scaling原理），本节进一步引入SE，给出2种KT实现思路.

3.1 时间尺度与尺度估计

所谓TS［12］，即连续信号x(t)到y(t)的映射过程，可表示为：

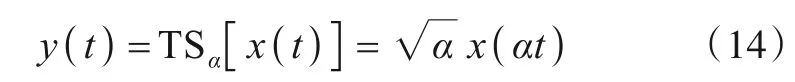
式中：TSα[·]为TS表示符号，α∈R+为尺度因子自变量，是为保持TS前后信号能量相同，即：

式（14）可理解为利用TS 操作，对原始信号进行拉伸或者压缩，以获得原始信号尺度版本，具体拉伸或者压缩程度由尺度因子决定.很明显，当0 ＜α＜1 时，TS后的信号时域扩张，当α＞1 时时域收缩.设连续信号z(t)=TSα1[x(t)]，α1为尺度因子确定值.所谓SE，即z(t)、x(t)已知时对α1的估计，可表示为：

式中：◇为尺度互相关符号，*为共轭转置符号.与时域互相关、频域互相关不同，Φzx(α)自变量为尺度因子，最大值对应的尺度因子即为尺度因子估计.从两个特例分析TS 对信号影响，设x1(t)为单频信号、x2(t)为线性调频信号，复数形式为：

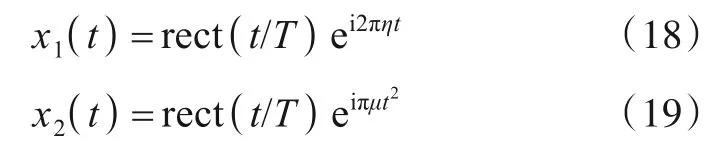
式中：η为x1(t)频率，μ为x2(t)调频斜率，T为时宽.易知：

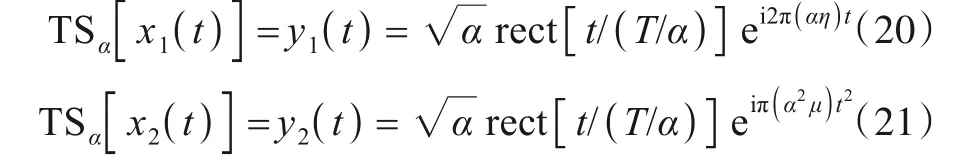
式中：y1(t)、y2(t)分别为x1(t)、x2(t)时间尺度后的信号.对连续信号做时间尺度，会改变信号幅度、时宽、频率（单频信号）和带宽（LFM 信号）.对于幅度的变化，离散化处理中如果要求TS 前后幅度相同，需对TS 后信号进行幅度调整；对于时宽的变化，如果要求采样点数相同，需对TS 后信号补零（α＞1）或截取（α＜1）；对于频率和带宽的增大（α＞1），为满足采样定理，应提高采样频率避免混叠.为直观显示，图1以时宽为1s的余弦信号为例，给出了尺度因子为0.5、2时的时间尺度和尺度估计示意图.

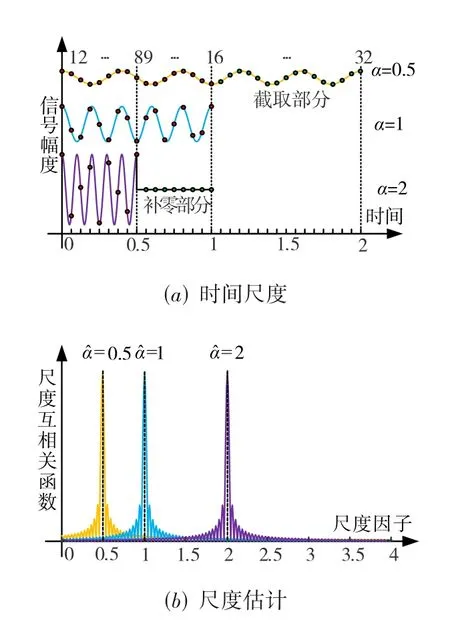
图1 时间尺度与尺度估计示意图

3.2 两种实现思路

取式（4）和式（5）慢时间部分，得到去耦前后回波慢时间信号分别为：

设x(f，tm)、y1(tm) 为连续信号，易知y1(tm) 为x(f，tm)的时间尺度，尺度因子为f0/(f+f0)，然后再调整幅度，具体可表示为：

当目标速度不模糊时，利用式（24）去耦合是合理的.当目标存在速度模糊时，将式（22）表示为：

式中：fd为目标不模糊多普勒频率，F为模糊数.去耦后的慢时间信号为：

为实现KT 去耦合，对x(f，tm)进行模糊数补偿（Fuzzy-number Compensation，FC），得到：

再进行时间尺度、调整幅度，具体可表示为：

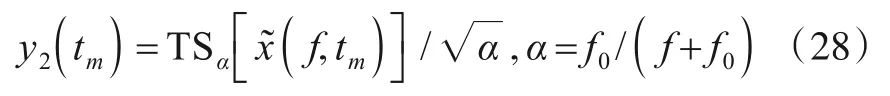
式（28）即为KT 的第1 种实现思路，将其命名为“FCTS”，该思路最早由文献［9］提出，文中的TS 环节利用两个级联的chirp 滤波器实现.当目标存在速度模糊时，“FCTS”思路面临模糊数搜索问题，传统方法是设定搜索区间，根据目标最大峰值确定模糊数，搜索区间的扩大会导致运算量成倍增加，针对该问题，文献［14］在文献［10］基础上，通过调整CZT 起始抽样点，降低了搜索运算量.在此产生1 个疑问，是否存在无需模糊数补偿的KT实现思路，重写式（25）：

进一步表示为：

4 Keystone变换的梅林域实现方法

为得到高效的KT，需要解决TS、SE 快速实现问题.实际上，TS 实现方法有很多种，文献［8～10］中的辛格插值、级联chirp 滤波等方法均可纳入TS 实现方法范畴，不同于上述方法，本文利用梅林变换解决TS 和SE快速实现问题.

4.1 梅林与尺度变换

梅林变换（MT）是一种积分变换，其出现时间较傅里叶变换要晚的多，近年来随着MT 理论的深入研究，已应用于目标识别［15］、尺度不变系统设计［16］等领域，广义MT表示式为：

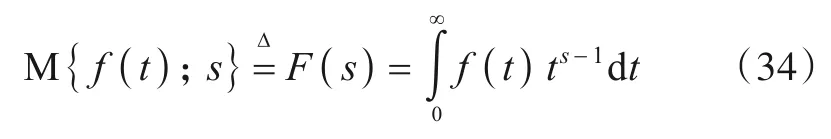
式中：M{·}为MT 表示符号，F(s)为信号f(t)的MT，自变量s=β-iζ为复数.当β=0.5时，MT 即为科恩提出的尺度变换［12］.ST表示式为：

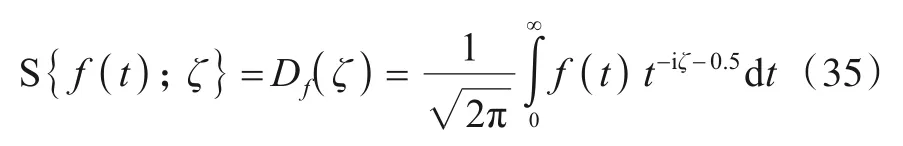
式中：S{·}为ST 表示符号，Df(ζ)为信号f(t)的ST，ζ为尺度，对应傅里叶变换中的频率.令t=eu，带入式（35），得到：

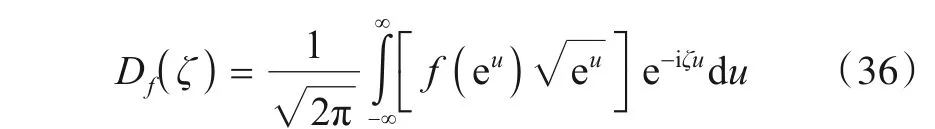
Df(ζ)为的傅里叶变换，可利用FFT 实现［17］，即快速尺度变换（Fast Scale Transform，FST）.逆尺度变换（Inverse Scale Transform，IST）：

IST 可利用IFFT 快速实现，即快速逆尺度变换（Inverse Fast Scale Transform，IFST）.FST 数值计算中要求对连续信号f(t)进行指数采样，对于现实的等间隔离散数据需要插值重采样，根据指数采样理论［18］，重采样信号长度应不小于NlnN，N为原始信号等间隔采样点数，结合FFT 操作可知FST 计算复杂度为O[(NlnN) log2(NlnN)]，总共需要的复乘次数为NlnN+0.5(NlnN) log2(NlnN)，IFST 计算过程与FST相反，先计算IFFT 再进行对数采样，计算量与FST相同.

4.2 TS与SE快速实现

设信号z(t)=TSα1[x(t)]，为解决TS 快速实现问题，引用ST尺度不变性，即：

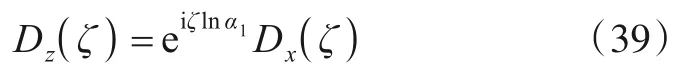
式中：Dx(ζ)、Dz(ζ)分别为x(t)、z(t)的ST，两者包络相同、相位不同.计算式（39）的IST，容易得到：

利用上式可得x(t)在某一尺度因子下的TS 后信号.SE同样利用ST快速实现［13］：

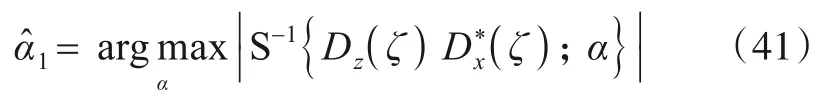
尺度互相关函数实现形式与脉冲压缩（时域互相关）快速实现相似，区别在于脉冲压缩是利用FFT、IFFT在频域实现，而尺度互相关函数是利用FST、IFST 在尺度域实现.需要注意的是，式（37）S-1{·}内的自变量为时间t，式（41）中为尺度因子α，两者物理意义不同.式（40）可知，利用ST 实现TS 需要进行1 次FST、1 次复数点乘和1 次IFST，总共需要进行的复乘次数为3NlnN+(NlnN) log2(NlnN)，式（41）可知，计算尺度互相关函数需要进行2 次FST、1 次复数点乘和1 次IFST，总共需要复乘次数为4NlnN+1.5(NlnN) log2(NlnN)，计算复杂度相同.

4.3 计算复杂度分析

为方便描述，采取“KT-实现思路-使用工具”方式，将现有3 种实现方法和所提3 种方法，依次命名为KTFCTS-SINC［8］、KT-FCTS-Chirp［9］、KT-FCTS-CZT［10］、KTFCTS-MCZT、KT-FCTS-MT 和KT-SETS-MT.设目标模糊数为F，回波信号经下变频、脉冲压缩、快时间FFT 得到M×P的二维矩阵，M为相参积累个数，P为快时间频率点数，偶数，利用上述方法对P个快时间频率单元回波进行去耦合处理，分析算法计算复杂度.

首先，分析现有3 种方法计算复杂度.KT-FCTSSINC 方法，为实现1 个快时间频率单元回波去耦合需要进行M2次复乘，结合模糊数补偿环节可知，该方法总共需要FP(M+M2)次复乘运算，计算复杂度为O[FPM2]；KT-FCTS-Chirp 方法，为实现1 个快时间频率单元回波去耦合需要进行2 次chirp 乘积、2 次chirp卷积，需要的复乘次数为FP(5M+3Mlog2M)，计算复杂度为O[FPMlog2M]；KT-FCTS-CZT 方法，为实现1个快时间频率单元回波去耦合，需要2 次chirp 乘积、1次 chirp 卷积和 1 次 IFFT，计算复杂度为O[FPMlog2M]，总共需要的复乘次数为FP(4M+2Mlog2M).

其次，分析所提KT-FCTS-MCZT 方法计算复杂度.该方法在计算1 个快时间频率单元回波CZT 时，区分CZT 比例系数γ≤1、γ＞1两种情况，当γ≤1时，需要进行4M+2Mlog2M次复乘运算，当γ＞1 时，需要进行M+3K+1.5Klog2K+0.5Mlog2M次复乘运算，K=fix(M/γ)为CZT采样点数，因此该方法总共需要的复乘次数为：

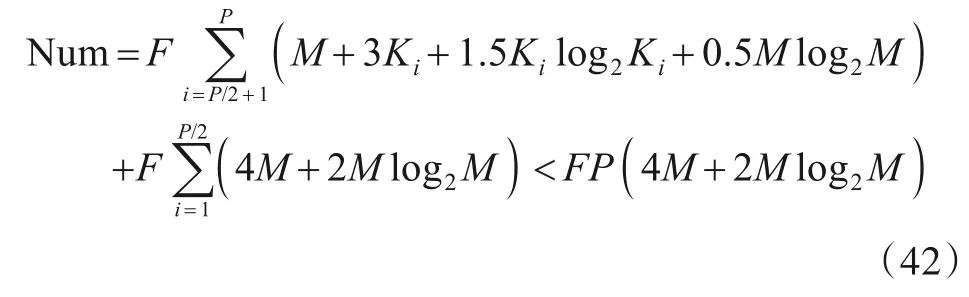
式中：Ki=fix(M/γi)为第i个快时间频率单元回波CZT采样点数，γi＞1 为对应的CZT 比例系数.上式可知，KT-FCTS-MCZT方法计算复杂度与KT-FCTS-CZT相同，但需要的复乘次数更少.

然后，分析所提KT-FCTS-MT 方法计算复杂度.该方法为实现1 个快时间频率单元回波去耦合需要进行1 次FST、1 次复数点乘和1 次IFST，复乘次数为(MlnM) log2(MlnM)+3MlnM，结合模糊数补偿环节可知，该方法总共需要的复乘次数为FP(M+3MlnM+(MlnM) log2(MlnM))，计算复杂度为O[FP(MlnM) log2(MlnM)].

最后，分析所提KT-SETS-MT 方法计算复杂度.该方法为实现1个快时间频率单元回波去耦合，需要进行3 次FST、2 次复数点乘和2 次IFST，复乘次数为7MlnM+2.5(MlnM) log2(MlnM)，由于无需模糊数补偿，该方法总共需要的复乘次数为

(P-1)(7MlnM+2.5(MlnM) log2(MlnM))，计算复杂度为O[P(MlnM) log2(MlnM)].设F=1，对比可知KT-FCTS-Chirp、KT-FCTS-CZT、KT-FCTS-MCZT方法计算复杂度最低，均为O[PMlog2M]，KT-FCTSMT、KT-SETS-MT 方法计算复杂度最高，均为O[P(MlnM) log2(MlnM)]，KT-FCTS-MCZT 方法所需要的复乘次数最少，KT-SETS-MT 方法所需要的复乘次数最多.

5 仿真与结果分析

5.1 参数设置

设窄带雷达载频1 GHz，重频10 kHz，相参积累个数为128，发射LFM脉冲信号，脉宽10 μs，带宽20 MHz，采样频率40 MHz；雷达探测范围内1 个高速点目标向站飞行，初始距离8 km，径向速度80 km/s.

5.2 仿真试验1

对所提KT-FCTS-MCZT、KT-FCTS-MT 方法可行性进行验证.脉冲压缩后回波一维距离像如图2 所示，目标存在明显的距离走动.根据式（27）对回波进行真实模糊数补偿，然后沿回波快时间频率做IFFT，结果如图3 所示，目标距离走动得到很大程度改善，但慢时间上仍未完全对齐.

图2 脉冲压缩后回波

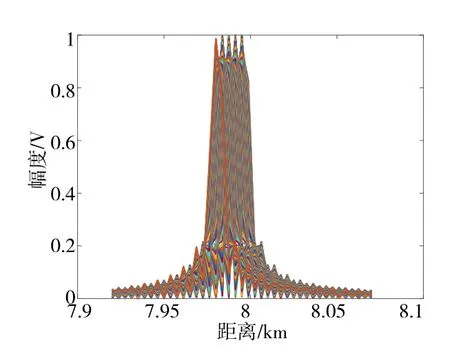
图3 模糊数补偿后回波

对图3 回波沿快时间频率做FFT，再利用所提KTFCTS-MCZT和KT-FCTS-MT方法校正目标距离走动，结果分别如图4、图5所示，目标在慢时间上完全对齐.

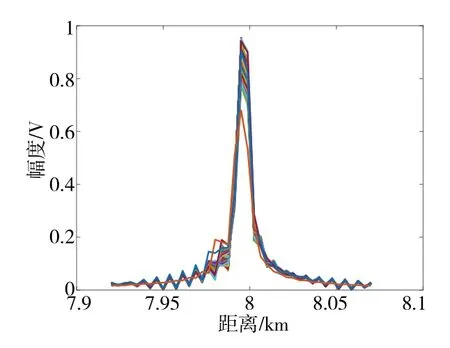
图4 距离走动校正结果（KT-FCTS-MCZT）

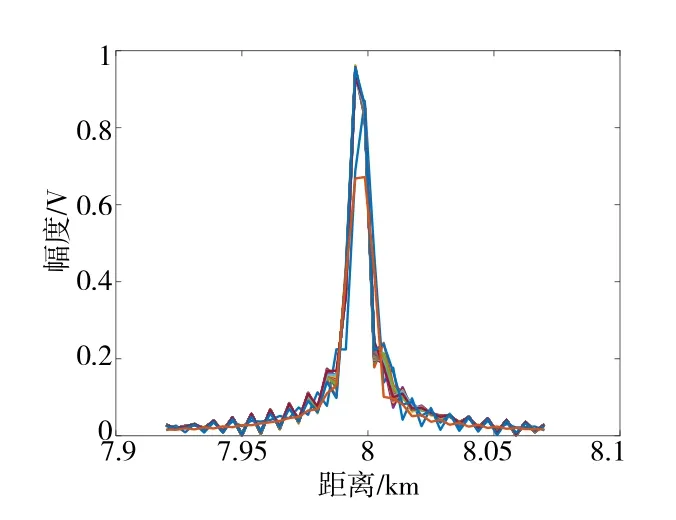
图5 距离走动校正结果（KT-FCTS-MT）

5.3 仿真试验2

本节对所提KT-SETS-MT 方法可行性进行验证.首先，沿快时间对脉压后回波快时间做FFT，结果如图6 所示，然后以快时间频率为0 MHz 的慢时间信号为匹配信号，对非零频慢时间信号进行尺度估计，结果如图7所示，图中每1列对应1个尺度互相关函数.

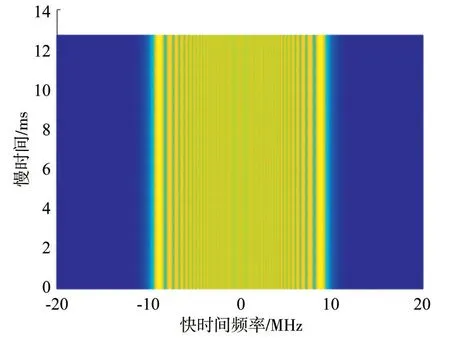
图6 回波快时间FFT

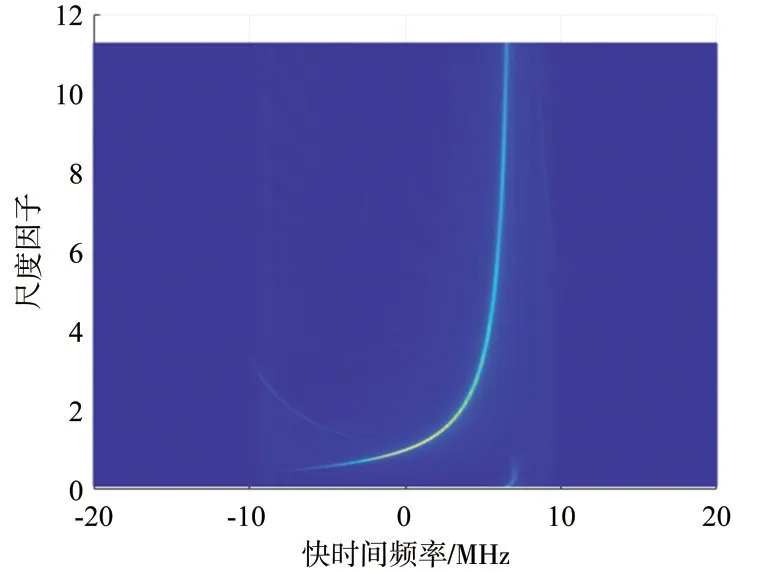
图7 回波慢时间尺度估计

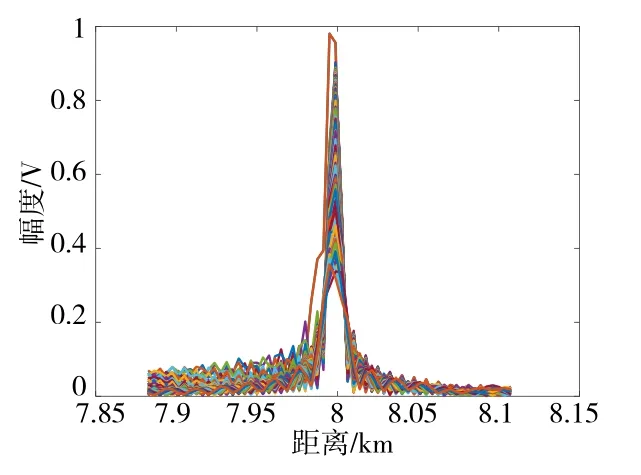
图8 距离走动校正结果（KT-SETS-MT）

5.4 抗噪效能分析

本节对比现有3 种KT 实现方法，对所提3 种方法抗噪效能进行验证.雷达积累脉冲数分别取128、160个，其他参数同5.1 节，信噪比（Signal to Noise Ratio，SNR）取值-20～5 dB，间隔2 dB，运行蒙特卡洛仿真500次，不同脉冲数下的目标检测概率（Target Detected Ratio，TDR）整体效果如图9（a）所示，将SNR 取值范围调整为-20～-15 dB，间隔0.5 dB，局部效果如图9（b）所示.

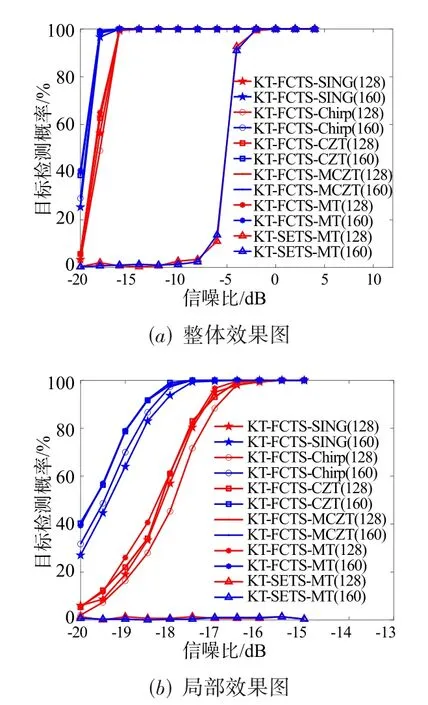
图9 不同脉冲数下的目标检测率曲线

同理设目标径向速度分别为50 km/s、80 km/s，其他参数同5.1 节，不同径向速度下TDR 曲线如图10 所示.进一步设雷达载频分别为0.5 GHz、1 GHz，不同载频下TDR 曲线如图11 所示.由2.2 节可知，KT-FCTSCZT 和KT-FCTS-MCZT 特定参数下存在频点丢失问题，本节使用参数能够确保模糊数补偿后的目标多普勒频率始终位于CZT采样区间内，不会出现频点丢失.

图10 不同径向速度下的目标检测率曲线

图11 不同雷达载频下的目标检测率曲线

综合图9（a）、10（a）、11（a）可以看出，前5 种KT实现方法抗噪性能相差不大，当SNR 大于-16 dB 时，不同参数下的TDR 均接近100%，而KT-SETS-MT 方法TDR 接近100%的临界SNR 为-2 dB，说明该方法不适用于低SNR 条件，分析原因是因为该方法需要对非零频慢时间信号进行尺度估计，然后再进行TS，由于缺乏峰值对比环节，算法受噪声影响更大.综合图9（b）、10（b）、11（b）可以看出，前5 种KT 实现方法抗噪性能基本相当，但也存在微小差距，总体上看，KT-FCTS-MT方法抗噪性能最优，KT-FCTS-CZT 与KT-FCTS-MCZT抗噪性能次之且基本相同，KT-FCTS-SINC 方法抗噪性能最差.同时可以看出，算法均受载频影响较大，载频越大目标检测效能越好，反之越差，分析原因是因为载频越大，KT 尺度因子越接近于1，即使不执行TS 操作，模糊数补偿后的目标回波慢时间仍能部分对齐，反之载频越小KT 尺度因子动态范围越大，模糊数补偿后的目标回波慢时间对齐数量也越少，目标距离走动校正效果受TS 执行精度影响也越大.

6 结论

围绕Keystone 变换快速实现问题，提出修正的“CZT+IFFT”方法，文中将其命名为KT-FCTS-MCZT.同时，利用梅林变换尺度不变和尺度估计特性，进一步提出2 种梅林域的Keystone 变换实现方法，依次命名为KT-FCTS-MT、KT-SETS-MT.仿真结果表明，窄带条件下，所提3 种方法均能实现雷达目标距离走动校正.KT-FCTS-MCZT 方法计算量最小，但存在频点丢失问题；KT-SETS-MT 方法无需模糊数补偿，但对信噪比要求较高；KT-FCTS-MT 方法抗噪性能最优，但计算量最大.另外，对梅林变换的功能开发和快速算法的改进是下步工作重点.