王 鼎，尹洁昕，郑娜娥，聂福全

（1.中国人民解放军战略支援部队信息工程大学信息系统工程学院,河南郑州 450001；2.中国人民解放军战略支援部队信息工程大学数据与目标工程学院,河南郑州 450001；3.国家数字交换系统工程技术研究中心,河南郑州 450002；4.卫华集团有限公司,河南长垣 453400）

1 引言

众所周知，目标定位技术在无线监测、地震勘测、紧急救助、安全管理等工业信息领域发挥重要作用［1～3］.依据观测站数量可以将目标定位系统分成单站定位系统和多站定位系统两大类，其中单站定位系统具有灵活性高、机动性强、系统简洁以及无需站间通信和同步等优点，本文主要研究单站定位方法.

单站定位系统常使用序列观测量进行定位，其中到达频率（Frequency Of Arrival，FOA）是常用的定位观测量，该观测量包含多普勒频移信息，可用于对窄带信号进行高精度定位.近年来，国内外学者提出若干基于FOA观测量的目标定位方法.文献［4，5］提出基于网格搜索的FOA定位方法，该类方法需要复杂运算，其定位精度和计算复杂度取决于搜索区间和步长.文献［6～8］提出基于信号数据的FOA直接定位方法，该类方法从传感器接收信号中直接获取目标位置坐标，需要多维迭代，易出现局部收敛和发散等问题，并且计算复杂度较高.文献［9］提出基于半正定松弛FOA定位方法，该类方法无需设置初始值，可避免局部收敛和发散，但需要凸松弛处理，因此其渐近统计最优性尚没有完备的理论做支撑，并且计算复杂度较高.为了避免迭代，文献［10，11］提出基于加权最小二乘估计的闭式定位方法，该类方法能获得目标位置向量表达式，但是其联合了FOA和到达角度观测量，因此观测站需要安装天线阵列.文献［12］提出一种加权辅助变量定位方法，其是一种可以有效削减估计偏置的FOA闭式定位方法，无需联合其他观测信息，但是该方法是以牺牲FOA观测量为代价，因此其估计方差无法渐近逼近克拉美罗界（Cramér-Rao Bound，CRB）.

上述定位方法均假设信号传播速度精确已知，但在某些场景中（例如水下声源定位、地震波定位等），信号传播速度可能无法精确获得，这将对定位方法产生较大影响，此时应将信号传播速度看成未知参数.文献［13］提出信号传播速度未知下基于到达时延观测量的无线传感网节点定位方法.文献［14］提出信号传播速度不等式约束下联合到达时延和到达角度观测量的无线传感网节点定位方法.文献［15～17］提出信号传播速度未知下基于到达时延差观测量的目标定位方法.事实上，信号传播速度除了决定信号传播距离外，还影响多普勒频移，文献［18］提出信号传播速度未知下联合到达时延差和到达频率差观测量的目标定位方法.上面提到的信号传播速度未知下的定位方法均可应用于水下声源定位场景，并且都需要分布式传感器来实现定位.文献［12，19］讨论了基于运动单传感器的水下声源定位方法，文献［9］中的静止多站FOA 定位方法也可等价为基于运动单站的FOA 定位方法，然而文献［9，12，19］中的方法都需要精确的信号传播速度，这在水下声源定位场景中难以得到满足.

基于研究现状，本文在信号传播速度未知下提出运动单站FOA定位新方法.该方法包含两个阶段，能实现目标位置向量和信号传播速度联合估计.本文还通过理论分析证明新方法参数估计均方误差可以渐近逼近CRB.

2 定位观测模型

假设在3 维空间中有单个运动观测站利用FOA 观测量对静止目标进行定位，该观测平台安装传感器，由于传感器与目标间的相对运动会使得FOA 观测量中包含多普勒频移，利用此信息可以对目标进行定位.传感器的运动轨迹由M个直线段构成，其在行驶第m条直线航迹过程中利用Nm个短时隙测量FOA，其中第n个短时隙获得的FOA表达式为

这里给出两点假设：（1）本文的单站定位区域并不宽广，可假定信号在不同时隙到达传感器的传播速度c保持不变，但需要将其看成是未知参数；（2）在每个短时隙内，传感器测量FOA 的时间足够短，使得传感器在每个短时隙内的位置变化量可以忽略不计.

实际中获得的FOA 观测量是含有误差的，其可以表示为

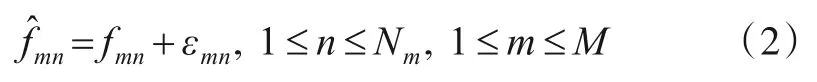
式中εmn表示FOA 观测误差.将式（2）合并成向量形式可得

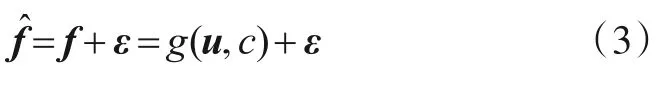
式（3）中，

3 参数估计方差的克拉美罗界

在本文的定位问题中，未知参数包括向量u和标量c，观测量为向量定义参数向量θ=[uTc]T，此时可以将对数似然函数表示为

式（5）中K表示与未知参数θ无关的常数.由式（5）可以得到关于参数向量θ的CRB表达式：

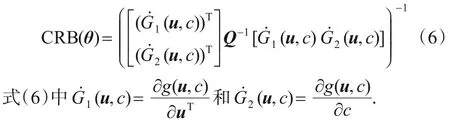
4 两阶段定位新方法

4.1 新方法的原理概述

文中的新方法包含两个阶段，每个阶段的基本原理描述如下：

（1）阶段1首先利用运动单站与目标间的几何关系构建第1组伪线性观测方程；然后利用该方程建立估计准则，并基于此实现向量u和标量c的解耦合优化，其中仅需对标量c进行1 维参数迭代，而向量u的解是以闭式解形式给出；最后分析估计结果的统计特性.需要指出的是，阶段1 中观测方程个数小于FOA 观测量个数N，因此其无法获得渐近统计最优估计值.

（2）阶段2 利用最初FOA 观测模型构建第2 组伪线性观测方程，并基于阶段1得到的估计值及其统计特性建立估计准则，进而获得参数向量θ的闭式解，该估计结果具有渐近统计最优性.

基于上面的原理概述，图1描述了新方法的总体技术路线.

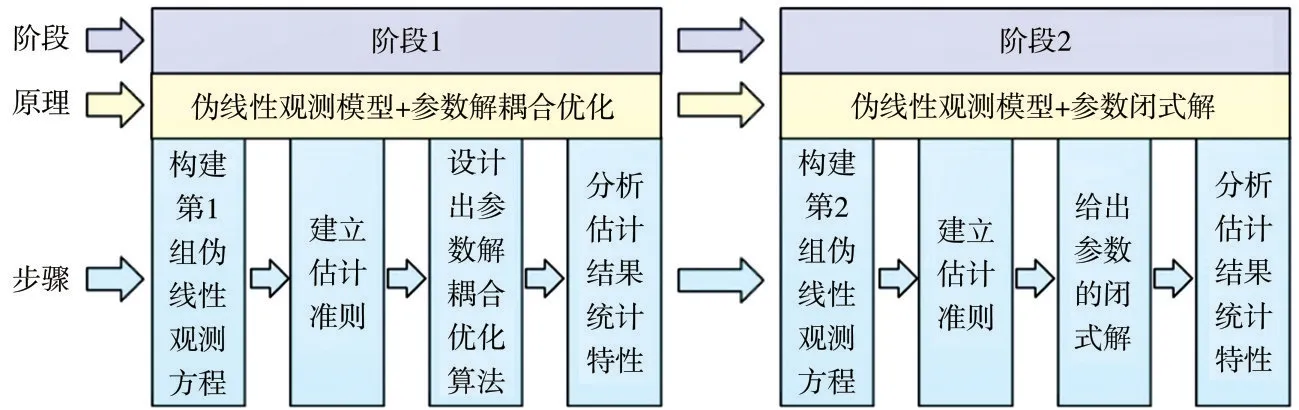
图1 新方法的总体技术路线图

4.2 阶段1的计算原理与方法

4.2.1 伪线性观测方程

这里借助几何关系推导第1 组伪线性观测方程.如图2 所示，定义向量u-smn与速度向量之间的夹角为βmn，则有

图2 定位几何关系示意图

结合式（1）和式（7）可得

由式（8）可知，夹角βmn与FOA 真实值fmn以及信号传播速度c有关.

在图2 中考虑由向量u、smn以及sm1构成的三角形，当n≥2时，利用三角形正弦定理可知

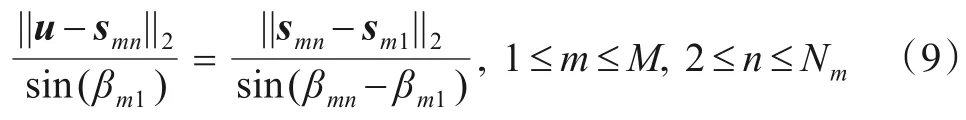
结合式（7）和式（9）可得

将式（10）写成矩阵形式可得

式（11）中，

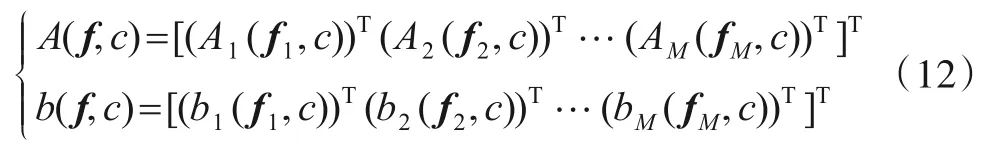
其中，

式（11）即为第1 组伪线性观测方程，其中A(f，c)表示伪线性观测矩阵；b(f，c)表示伪线性观测向量.

由于式（10）仅在n≥2 时成立，从而导致式（11）中包含的方程个数仅为N-M，小于FOA 观测量个数N，因此基于式（11）无法获得渐近统计最优的定位结果，但是其作为新方法的中间步骤仍然不可或缺.

4.2.2 估计准则及其求解算法

建立合理的估计准则需要分析伪线性观测方程中的误差特性，为此定义如下伪线性观测误差向量

将式（16）和式（17）代入式（15）中可知

式（20）中，

由式（20）可知，误差向量ξf渐近服从零均值的高斯分布，并且其协方差矩阵为

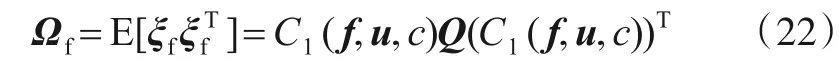
结合式（15）和式（22）可以建立如下加权最小二乘估计准则：

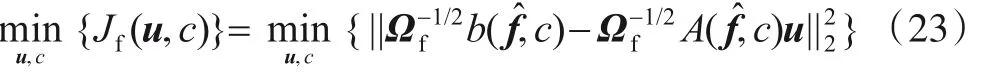
为了减少参与迭代的变量维数，这里提出利用解耦合优化的思想对式（23）进行求解.首先可以得到向量u在阶段1的最优表达式：

然后将式（24）代回式（23）中可以得到仅关于标量c的优化问题

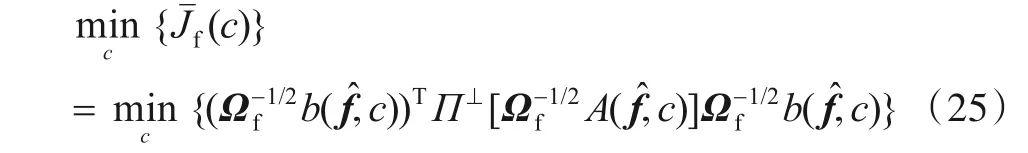
式（25）中，Π⊥[·]表示矩阵列补空间上的正交投影函数.式（25）是一维优化问题，可以通过Newton-Raphson 迭代法进行求解，相应的迭代公式为

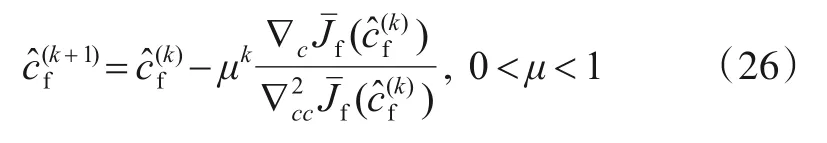
式（26）中，

4.2.3 理论性能分析

下面推导阶段1中的估计值的统计特性，具体结论可见如下两个定理.

证明将式（22）代入式（28）中可得

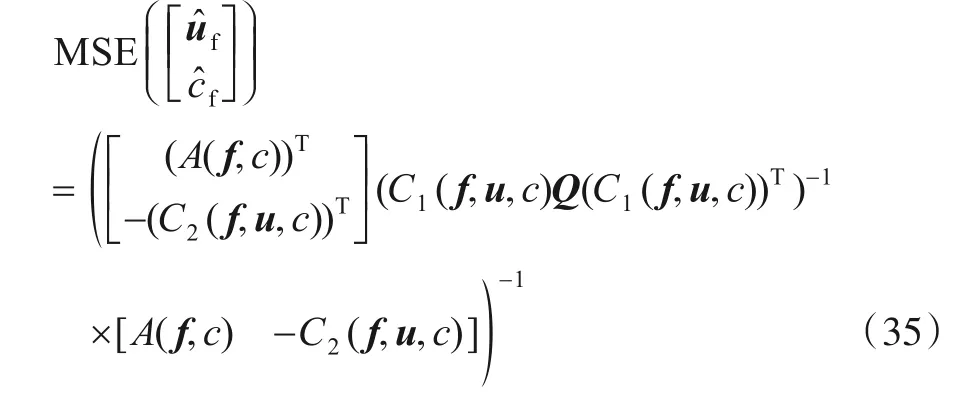
另一方面，将定义式f=g(u，c)代入式（11）中可知

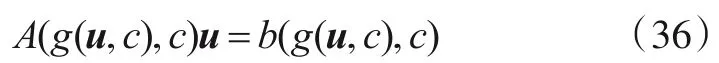
将式（36）两边分别对u和c求导可得

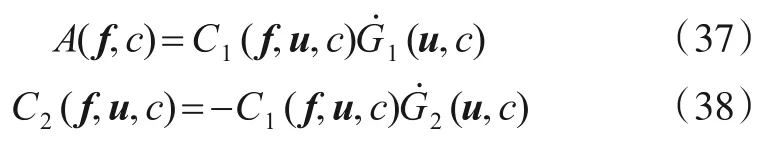
将式（37）和式（38）代入式（35）中可知

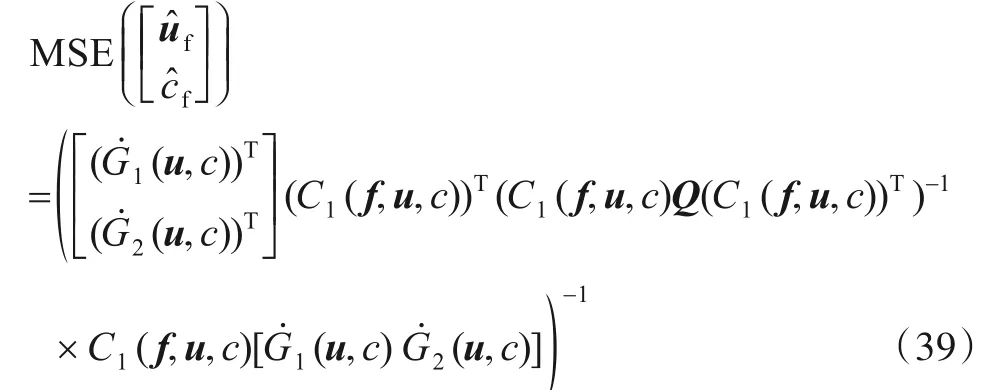
结合式（6）、式（39）以及矩阵不等式A-1≥B(BTAB)-1BT（其中，A为任意正定矩阵；B为任意列满秩矩阵）可得

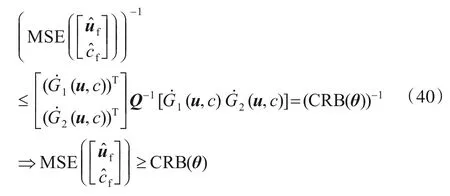
证毕.

定理2 表明，观测方程个数的降低使得阶段1 的估计值不具备渐近统计最优性，因此下面还需要利用阶段2对此估计值进行优化更新，旨在获得具有渐近统计最优性的估计结果.

4.3 阶段2的计算原理与方法

4.3.1 伪线性观测方程

若要获得渐近统计最优的定位精度，就不能减少观测方程个数，为此需要回到最初FOA 观测模型式（1）中，并将其进一步转化成如下形式：

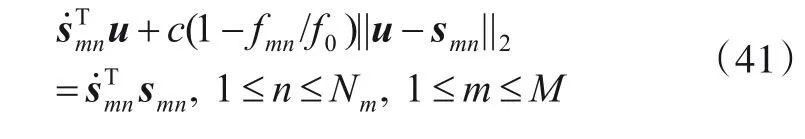
将式（41）写成矩阵形式可得

式（42）中，

式（42）即为第2 组伪线性观测方程，其中H(f，u)表示伪线性观测矩阵；w表示伪线性观测向量.

式（42）与式（11）的根本区别在于，式（42）中的方程个数等于FOA 观测量个数N，没有信息损失.事实上，在本文的新方法中，式（11）与式（42）都不可或缺.式（11）的意义为，提供渐近统计无偏估计值及其统计特性，正是基于此信息，才可以将式（42）中的观测矩阵H(f，u)看成已知量，进而在阶段2 中得到参数向量θ的闭式解；式（42）的意义为，提高阶段1的估计精度，并获得渐近统计最优估计值.

4.3.2 估计准则及其最优闭式解

首先定义如下伪线性观测误差向量：

式（46）中，

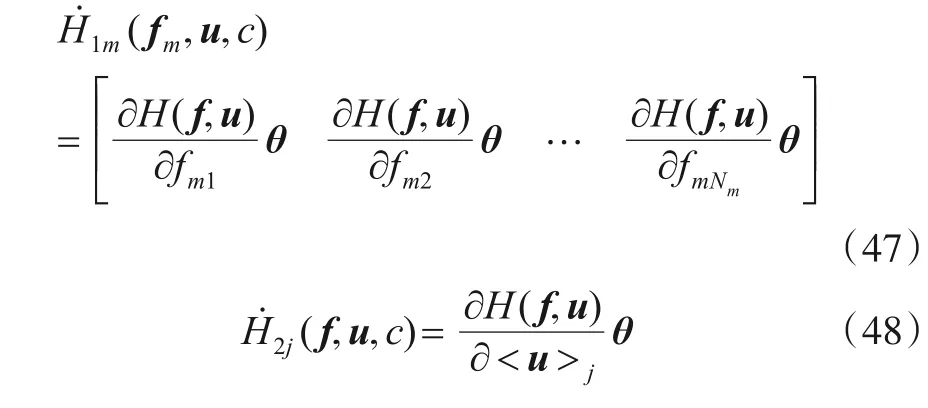
将式（31）和式（46）代入式（45）中可知

式（49）中，

由式（49）可知，误差向量ξt渐近服从零均值的高斯分布，并且其协方差矩阵为

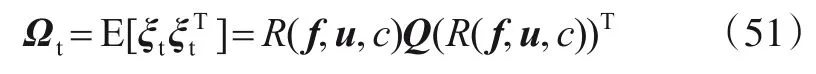
结合式（45）和式（51）可以建立如下加权最小二乘估计准则：

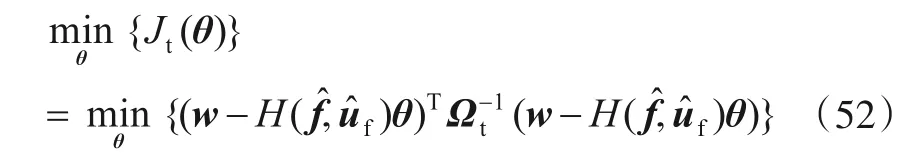
式（52）的最优闭式解为

5 定位新方法的理论性能分析

在一阶误差分析框架下，由式（55）可以进一步推得

证毕.

定理4向量是关于参数向量θ的渐近统计最优估计值，即有

证明将式（51）代入式（54）中可得

对比式（6）和式（58）可知，下面仅需要证明等式：

首先结合式（32）、式（33）以及式（50）可得

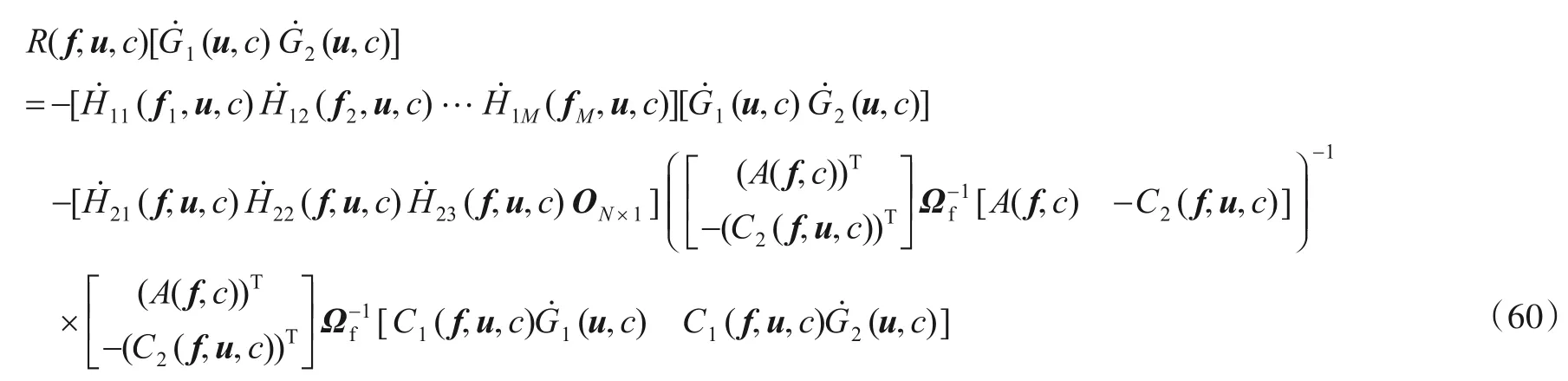
将式（37）和式（38）代入式（60）中可知

另一方面，将定义式f=g(u，c)代入式（42）中可得

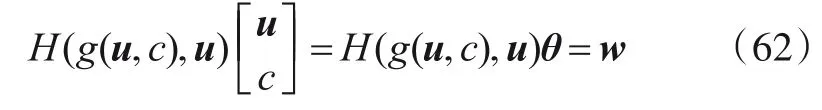
将式（62）两边分别对u和c求导可知

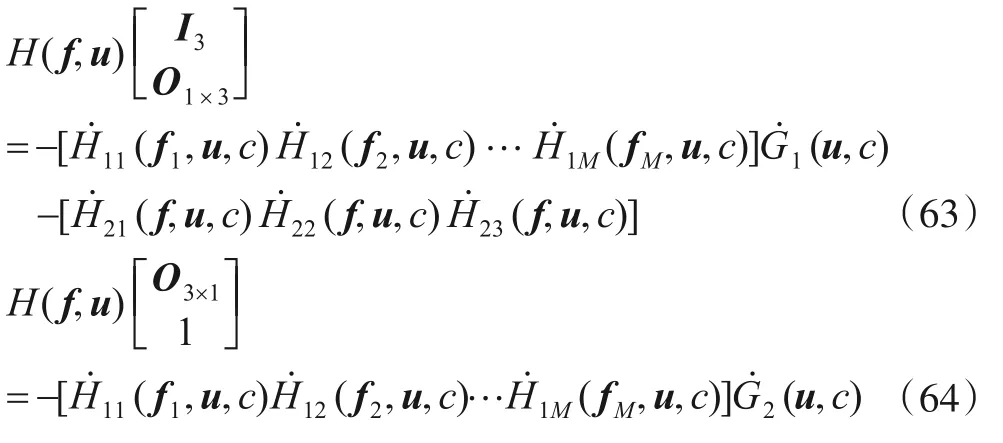
将式（63）和式（64）合并可得

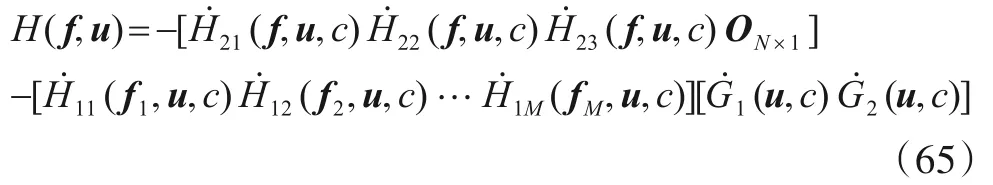
结合式（61）和式（65）可知式（59）成立.

证毕.

6 仿真实验与结果分析

基础实验场景如下：假设水下目标位置向量为u=[-200 200 300]Tm，水下目标信号发射频率为f0=25 kHz，现利用单观测平台对其进行定位，该平台在水下行驶4 条直线航迹，每条航迹利用6 个短时隙获得FOA 观测量，短时隙位置坐标见表1 和表2，该平台行驶每条直线航迹时的速度见表3.FOA 观测误差服从均值为零、方差为的高斯分布，其中σf表示标准差.

表1 第1条和第2条航迹中的12个短时隙位置坐标

表2 第3条和第4条航迹中的12个短时隙位置坐标

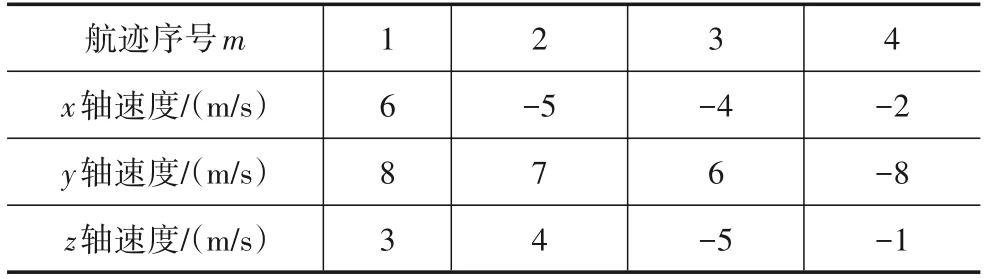
表3 每条航迹的速度

6.1 验证新方法的渐近统计最优性

首先设信号传播速度为c=1500 m/s，改变目标位置，在[-250 m -150 m]×[150 m 250 m]×[250 m 350 m]区间内服从均匀分布.图3 给出新方法的定位均方根误差及其CRB 随着FOA 观测误差标准差σf的变化箱线图.

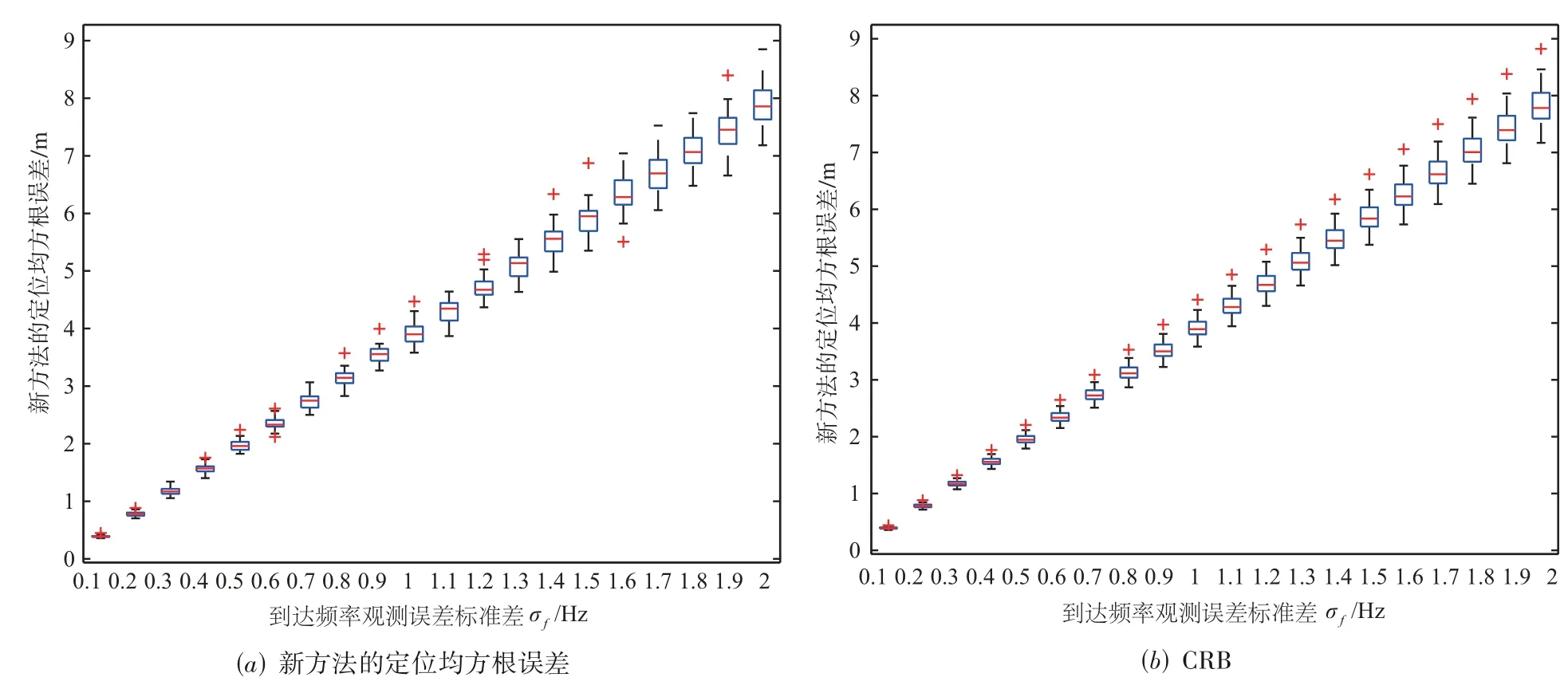
图3 新方法的定位均方根误差及其CRB随着FOA观测误差标准差σf的变化箱线图（目标位置坐标服从均匀分布）

然后假设目标位置向量为u=[-200 200 300]Tm，改变信号传播速度，并参照文献［13～18］中的参数设置，令其在[1400 1600]m/s 区间内服从均匀分布.图4给出新方法的定位均方根误差及其CRB随着FOA观测误差标准差σf的变化箱线图.

图4 新方法的定位均方根误差及其CRB随着FOA观测误差标准差σf的变化箱线图（信号传播速度服从均匀分布）

从图3 和图4 中可以看出：（1）新方法的定位均方根误差能够渐近逼近CRB，从而验证了新方法的渐近统计最优性；（2）新方法的渐近统计最优性对于目标位置坐标和信号传播速度具有一定泛化性.

6.2 与已有定位方法进行比较

这里比较的方法包括泰勒级数迭代定位方法（涉及迭代初始值无误差和迭代初始值有随机误差两种情形）和文献［9，12］中的定位方法.需要指出的是，文献［9，12］中的定位方法假设信号传播速度精确已知，因此需要设定信号传播速度，这里取典型值c=1500 m/s.此外，新方法与泰勒级数迭代定位方法均能对目标位置向量和信号传播速度进行联合估计，因此无需对这两种方法预先设定信号传播速度的数值.

首先假设信号传播速度为c=1470 m/s.图5 给出了目标定位和信号传播速度估计均方根误差随着FOA 观测误差标准差σf的变化曲线.

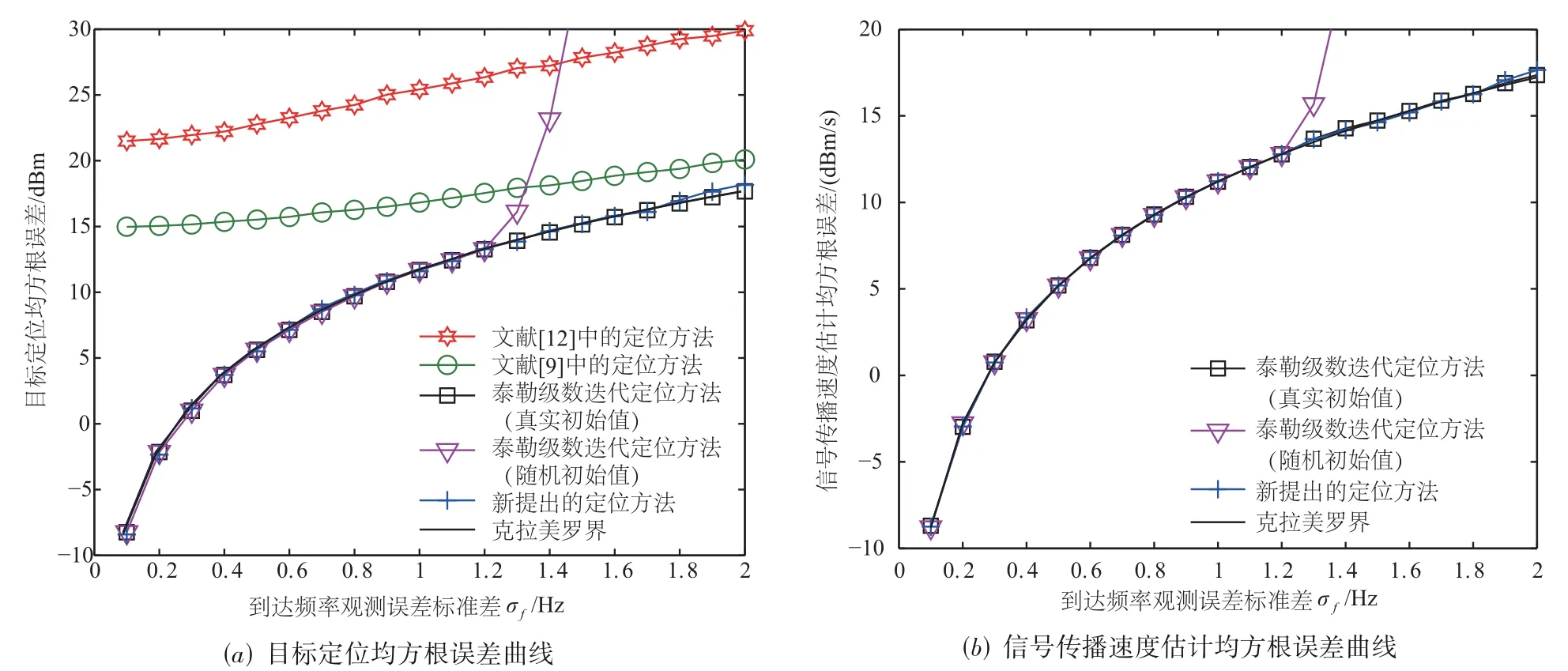
图5 目标定位和信号传播速度估计均方根误差随着FOA观测误差标准差σf的变化曲线

然后假设FOA 观测误差标准差为σf=1 Hz.图6给出了目标定位和信号传播速度估计均方根误差随着信号传播速度c的变化曲线.

从图5 和图6 中可以看出：（1）新提出的定位方法的性能可以渐近逼近CRB；（2）对于文献［9，12］中的定位方法，当信号传播速度的真实值偏离预先设定的典型值c=1500 m/s 时，两种方法的定位性能都会显著下降，并且速度偏差值越大，定位误差越大（见图6），当信号传播速度的真实值等于预先给定的典型值c=1500 m/s 时，文献［9］中的定位方法的性能接近CRB，但文献［12］中的定位方法始终无法逼近CRB，这是因为后者虽然能够获得目标位置向量的闭式解，但是以牺牲FOA 观测量为代价，因此其并不具有渐近统计最优性，这与文献［12］中的结论一致；（3）当泰勒级数迭代定位方法的初始值存在随机误差时，其产生“门限效应”的误差阈值明显低于新提出的定位方法，这是因为泰勒级数迭代定位方法是针对最初FOA 观测方程进行迭代的，其中没有推导伪线性观测方程，因而难以获得合理的初始值，初始值中的随机误差很可能导致迭代发散，此时经有限次统计得到的定位均方根误差会出现“陡增”现象（即门限效应）；（4）当泰勒级数迭代定位方法取真实值作为迭代初始值时，其估计精度与新方法接近，但将真实值作为迭代初始值在实际应用中难以实现.

图6 目标定位和信号传播速度估计均方根误差随着信号传播速度c的变化曲线

7 结论

本文在信号传播速度未知下提出基于运动单站FOA 观测量的目标定位新方法.该方法共包含两个计算阶段，其中的迭代过程仅涉及一维参数优化，无需设置目标位置向量初始值，并能实现目标位置向量和信号传播速度联合估计.此外，文中通过理论性能分析证明新方法的参数估计精度可以渐近逼近CRB.仿真实验结果表明，新方法具有渐近统计最优性，其性能优于文献［9，12］中的定位方法，并且与迭代初始值取真实值的泰勒级数迭代定位方法相近，但新方法仅需对信号传播速度进行迭代，其计算复杂度更低.