植被斑图动力学系统的参数反演
2022-07-05罗心悦
罗心悦,陈 瑜
(1. 复旦大学 数学科学学院,上海 200433; 2. 上海财经大学 数学学院,上海 200433)
植被斑图(Vegetation pattern)是世界上诸多干旱半干旱地区常见的景观特征,通常形成于年降雨量50 mm到750 mm的地区,受降水、地质地形、土壤和植被的空间异质性及人类活动的影响,呈条带状、圆环状、斑点状等结构。植被斑图不仅能够维持干旱半干旱地区能量与物质的循环过程,还能防止风蚀荒漠化。植被格局反映了干旱半干旱区生态系统的生态水文过程,为沙漠化等生态系统转型提供预警指标。因此,研究植被斑图的组成结构、形成机制以及演替过程,正确认识生态系统的关键因子及各因子之间的相互关系,对于揭示干旱半干旱区生态系统变化的关键过程具有重要意义。这将有助于预测气候变化对荒漠地区生态系统的影响,为地区生态环境建设形成绿色发展模式提供重要的理论基础和技术支撑。
在理论分析方面,非线性科学的进步带动了斑图动力学的发展。反应扩散方程是非线性系统研究中的一个重要分支,在化学实验控制、生物识别、期权定价、影像分析等众多前沿科学领域有重要应用。反应扩散模型能够模拟反应扩散过程中丰富的空间动态模式,因而其衍生出的各类问题一直为数学家和物理学家重点关注。学者们探究了生态水文过程、资源的空间再分配、植物个体间的空间相互作用,以及气候和管理条件等因素对植被格局的影响[1]。即使在地形和土壤没有表现出任何异质性的情况下,仍可以观察到植被格局的形成,这说明植被格局是内在植被动力学的结果[2]。1999年,Klausmeier[3]提出刻画斜坡上植被格局的数学模型,基于该模型对斜坡上呈条纹状和点状斑图模式的成因进行解释,并结合数值模拟得到条纹状和点状的空间斑图。
目前对植被斑图模型的数值研究主要集中在两方面: 一是利用微分方程理论对模型的解进行定性研究,以及利用数值方法获得模型近似解析解或高精度数值解;二是在已知模型并且获得部分观测数据后,确定最优模型参数,即参数反演。前者属于正问题研究,后者在反问题研究范畴内。观测信息的不准确和模型自身的耦合、非线性等特性,都为反问题的求解增加难度。因此,基于有限的观测对模型参数进行准确、稳定地反演,识别出植被格局的演化特征,具有重大的现实意义。
1 植被斑图模型的正演
考虑广义Klausmeier-Gray-Scott模型。如图1所示,模型刻画带有土壤水扩散反馈调节机制的平原地区植被斑图的演化过程:

图1 模型示意图Fig.1 Model diagram
式中符号、参数的解释说明如下:w、b为2维空间(x,y)随时间t变化的水量和植被量;Δ是拉普拉斯算子,DwΔw、DbΔb分别表示水和植被的扩散,参数Dw、Db为各自的扩散系数;A刻画降水;Lw刻画水汽蒸发,参数L为蒸发水平;Rwb2表示支持植物生长的水份供给,也表示植物的生长,参数R为供给水平;Mb刻画植被的消亡,参数M为植被的死亡率;Ω是边界∂Ω光滑的有界区域;初始条件φ(x,y)和ψ(x,y)是非负函数;v表示水在负方向的下坡径流量。
不失一般性[4],对参数空间进行简化,令L=R=1,即有
(1)
2 数值模拟与分析
本文采用了如下所示的1阶半隐式后向欧拉差分格式(First-order semi-implicit backward Euler difference scheme)[5]:

在MATLAB程序中,空间步长取1,时间步长取0.05,水的扩散系数Dw取10,植被的扩散系数Db取1,总时长T取30。图2为2维区域Ω=(0,400)×(0,400)内终时植被的空间分布图,A分别取0.48、0.52、0.45。我们可以看到当降雨量A接近阈值(A=0.50)时,缓慢的植物扩散和快速的水分扩散可以演化出一种临界的植被状态——植被集中于小区域。其中,蓝色区域为裸土(b=0),红色区域为高植被密度区域。当降雨量增加时,不同初始状态的植被分布演变出图3所示的斑点状、条带状、迷宫状等具有自组织(Self-organized)特征的模式。

图2 降水量处于阈值时聚集型植被分布Fig.2 Distribution of aggregated vegetation when precipitation is at threshold
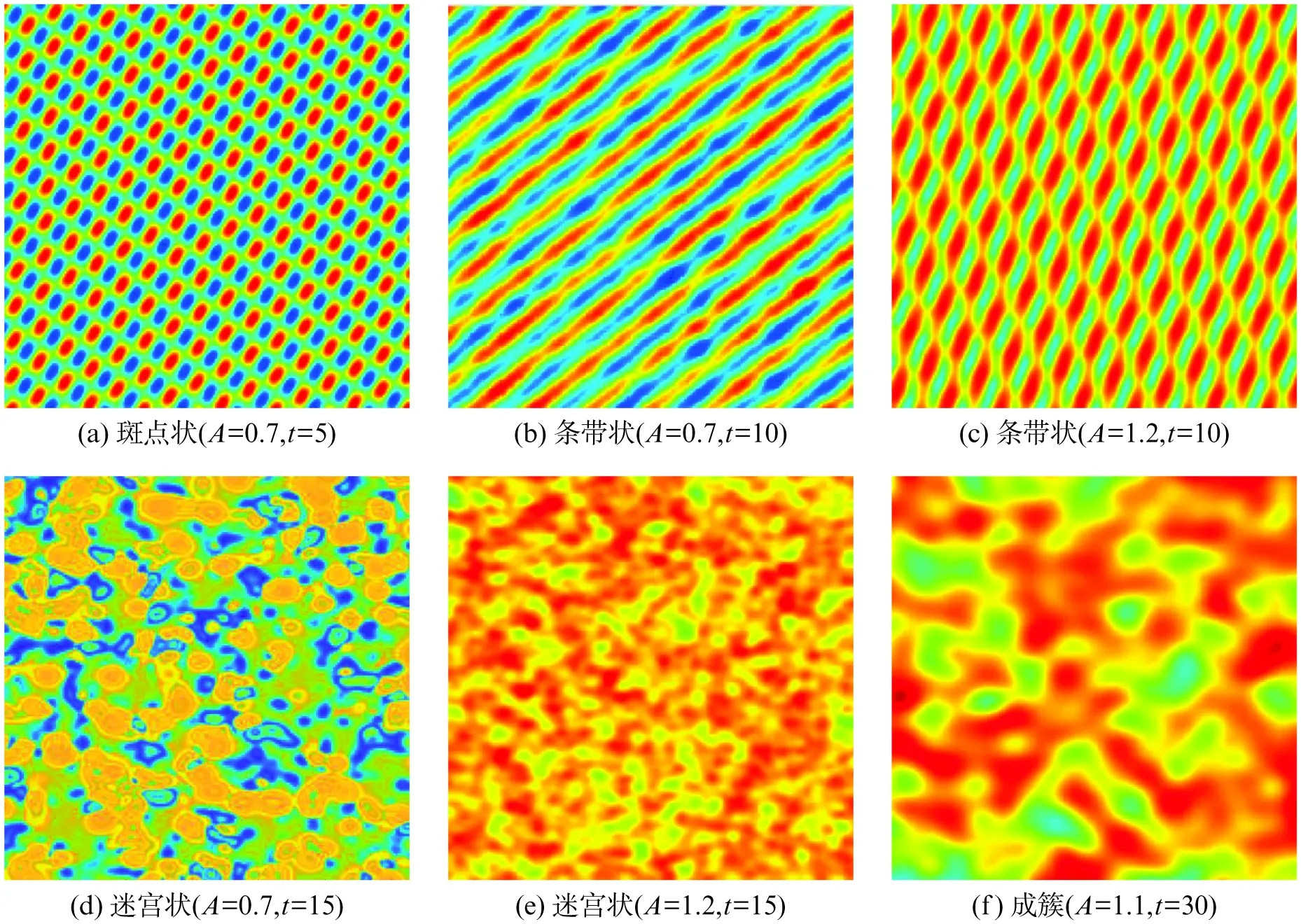
图3 不同形态的的植被模式Fig.3 Different vegetation patterns
图3中,初始条件设定为
w(x,0)=0.6+0.15cos(2π(0.5x×y))+0.3sin(2π(0.5x+0.4y×R)),b(x,0)=0.5+0.12cos(2π(0.5x×y))+0.2sin(2π(0.4x+0.5y×R))。
式中:R是服从高斯分布N(0,1)的随机数矩阵,且令初始矩阵中为负数的元素为零。再选取参数Dw=10,Db=1,A=0.9,M=0.45。令初始条件为
w(x,0)=0.2+R,b(x,0)=0.3+R。
图4展示了该设定下植被斑图的演变过程。从图4中可以看到,在演变初期,系统变化较大,具有一定的振荡,随着时间推移,系统趋于平稳,斑图形状基本稳定。

图4 特定参数取值下植被格局的时空演变Fig.4 Spatiotemporal evolution of vegetation pattern under specific parameters
为探究不同参数对系统最终状态的影响,本文对系统主要参数A,M进行了灵敏度分析,结果如图5所示。纵坐标为各格点的植被密度b的总和btotal,代表观测区域的植被密度大小。

图5 主要参数对整体密度的影响Fig.5 Influence of main parameters on overall density
从图5可以看到,降水量、植物死亡率的变化能够引起区域内植被密度的大幅波动。因此,对A、M的精确识别对于植被系统的预测与控制具有重要的意义。
3 植被斑图系统参数反演算法
我们分别记降水量A和植物死亡率M两个参数为
c1=A,c2=M。
根据观测条件的不同,参数识别问题可以细分为终时观测的参数反演问题与间断观测的参数反演问题[6]。显然,反演参数A、M均具有上界,因此,我们规定参数的可行域:
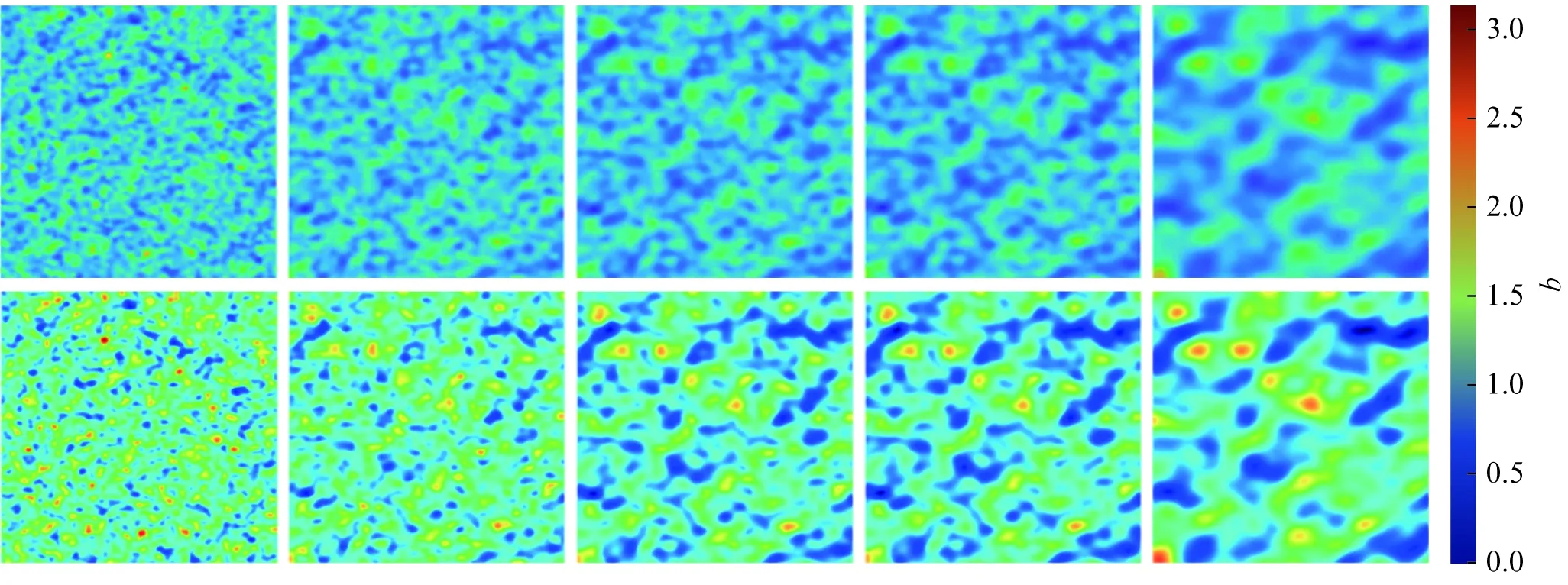
Uad={(c1,c2)∈2:0 (2) 其中不等式右端的C1和C2是由有关图灵系统的适定性分析所确定的。正问题陈述如下: 正问题对于可行域Uad中给定参数(c1,c2),计算满足系统(1)的水浓度w(x,t)和植被密度b(x,t)。 (3) 其中:J被定义为 以反应扩散系统(1)为约束条件。由γi加权的项度量了在T时的系统解与观测值之间的差异。由λi加权的项有效地限制了参数c1,c2的大小,这既满足式(2)的要求,又对观测噪声有一定容许度。通过使用λi加权项进行反演的过程被称为Tikhonov正则化。使用Tikhonov正则化一定程度上可以避免偏微分方程相关反问题可能出现的不适定性[7]。对于正则化参数的选择有诸多方法,例如L-曲线方法(L-curve method)。正则化参数的最佳选择的讨论可以参考文献[8],本文不做赘述。通过选取正则化参数,我们可以平衡方程的拟合与参数的大小控制。现在,我们给出反问题的陈述: 根据最优控制理论,本文引入了伴随系统(Adjoint system): (4) 式中:p(x,t)(简记为p),q(x,t)(简记为q)为伴随变量,且 由于伴随方程在时间上是倒向的,因此需要最终条件而不是初始条件。最终条件为 此外,我们由伴随系统得到关于伴随变量的最优控制的显式表征,即最优条件: (5) 状态方程(State Equation, SE)(1)和伴随方程(Adjoint Equation, AE)(4)以及最优条件(5)称为最优系统(Optimality system)。可以证明映射(c1,c2)(w,b)是Gteaux可导的,并且其导数满足 3.1.1 变步长梯度算法 为求解参数反演问题,本文首先考虑用文献[10]中提到的变步长梯度算法(Variable step gradient algorithm)获得最优解和最优参数的近似。算法对状态方程、伴随方程和终时T处的目标函数进行了离散处理。具体地,算法首先对参数c1(0),c2(0)进行初始化设定,并且预设迭代步长λ以及用于检验成本函数收敛性的误差容限ε。在每次迭代中,算法求解w(k),b(k)(k≥1)的非线性反应扩散系统,并储存损失函数J(c1(k),c2(k))。与此同时,算法还计算了伴随变量的值p(k),q(k),以及损失函数c1(k),c2(k)的导数dJ(c1(k),c2(k))/d(c1(k),c2(k))。如果成本函数减小,依照适当的步长λ沿该方向继续计算;如果成本函数没减小,则减小步长λ。在确定好新步长后,通过标准的梯度算法对参数进行更新: 重复这一步骤,直至损失函数的相对误差小于容限,即 式中:JN(k)指第k次迭代中时间节点N处的损失函数。但考虑到上述迭代算法可能出现停滞的状况,我们设计异常处理: 如果步长小于误差容限,即λ<ε,则退出算法。离散最优控制算法的每次迭代都需要状态方程的数值解到终时T,伴随方程的数值解从终时T开始向前求解,梯度更新。该最优化问题的标准算法计算成本巨大。但由于目标函数的最优解是系统的平稳解(Stationary solutions),上述标准算法可以改进为: 选择与目标函数相等的状态方程的初始值,取最终时间T仅等于2个时间步长τ并寻找对应于平稳初始数据的参数c1(k)和c2(k)。改进算法的其他步骤与标准算法步骤基本相同。改进算法的逻辑很容易理解,如果参数c1(k)和c2(k)是最优的,则2个时间步2τ后的损失函数为零,算法停止;如果参数c1(k)和c2(k)是次优的,则初始数据在2个时间步长2τ上演化,然后通过损失函数衡量系统解和目标方程之间的差异,通过调整参数优化变步长梯度算法。 3.1.2 数值结果 在数值实验中,本文发现标准梯度算法的运算时间对初值的选取具有较强的依赖性,迭代过程容易陷入停滞,无法收敛。然而改进梯度算法收敛于几乎所有初始值,并且能在较短时间内精确估计出用于生成观测值的参数值。表1显示了标准梯度算法(参数用Asd,Msd表示)和改进梯度算法(参数用Amd,Mmd表示)的数值结果,后者具有更显著的准确率。 表1 参数反演结果Tab.1 Parameter inversion results 为验证算法的收敛性,本文绘制了损失函数fLoss随算法迭代的变化图像,如图6所示,k迭代表示算法的迭代次数。对于改进梯度算法,损失函数在最初的几次迭代中快速下降,在此之后维持在较低水平;对于标准梯度算法,由于在每次梯度更新中算法都以恒定步长计算多步,所以损失函数整体趋势在下降,但存在一定的振荡。 图6 算法的残差-步数曲线对比Fig.6 Comparison of residual-iteration curve of two algorithms s取0对应不含噪音的观测值函数。图7(见第330页)展示了含1%水平噪音的观测图像以及根据改进梯度算法重构出的终时植被斑图。从图中可以看到,重构算法能够较好地还原出原始观测中植被浓度较高的区域,并保持植被分布的基本形状。 图7 终时植被斑图的观测及重构Fig.7 Observation and reconstruction of terminal vegetation pattern 综上,改进梯度算法能够有效地从含噪终时观测中得到参数估计。然而在现实中,植被演化的终时观测是难以获得的,更多的情形是,可观测数据来源于遥感探测器,研究者们需要从离散的观测数据中分析出系统演化特征,然后对未来发展趋势进行预测。使用确定性算法,相当于对每一间断观测进行最优参数求解,没有很好地利用观测的历史信息,甚至可能出现相邻两次求解结果悬殊较大的情况,因此需要更科学的方法为植被防护提供支持。 3.2.1 数据同化及贝叶斯理论基础 数据同化(Data assimilation)是基于观测信息结合数学物理模型模拟动态变化的一种方法,应用于复杂系统的建模和对发展趋势的预测,其目的是同化观测数据,为预测提供尽可能准确的可信区间[11]。数据同化基于概率对模型状态变量和参数进行最优估计,为模型的规律探寻和预测提供了一条有效的途径。在这个意义下,贝叶斯定理(Bayesian theory)是数据同化方法的理论基础。 贝叶斯理论的主要思想是根据已有的观测信息修正原有判断,从而得到关于模型的后验概率分布。对于参数反演,研究问题具有三大要素,分别是数据(观测值)、关键参数和数学模型。基于偏微分方程的泛函分析框架,数据和参数可以认为是Banach空间中的元素,即假设U和Y是Banach空间,y∈Y是数据,p∈U是参数。一般来说,p代表参数向量。当参数值p确定时,可以对模型进行求解,计算出与该参数对应的模型解。这个过程被称为正问题的求解,而参数反演问题是一个反问题。正问题的求解可以表示为如下映射: G:U→Y。 由于G将参数映射到测量空间(Measurement space),因此G称为观测算子(Observation operator)。如果对于每一个参数组,模型存在唯一解,G在空间U中是良定义的;倘若G为多值函数,则G在U中不是良定义的。 实际上,数据中常存在着一定水平的噪声,可以通过概率分布来进行建模。设噪声η服从概率分布0,进而观测值可以表示为 y=G(p)+η。 (6) 式(6)表示了数据y的概率分布与参数p和噪声η之间的关系,参数反演问题的三大要素串联了起来。从建模的角度来看,只要数据y位于Banach空间中,式(6)具有良定义的性质。在Banach空间的假设下,我们能够得到参数反演问题的严格证明,并且结果适用于解的数值近似[12]。 在贝叶斯理论框架下,系统(1)的参数反演问题又可以陈述如下: 令μy为(p|y)的概率密度函数(Probability density function),(y|p)的概率密度函数由ρ(y-G(p))给出,其中ρ是噪声分布0的概率密度函数。用μ0表示先验分布0的概率密度函数。根据贝叶斯定理,我们得到 μy(p)∝ρ(y-G(p))μ0(p)。 贝叶斯定理表明,假设势Φ:U×Y→是在乘积测度0×0可度量的,并假设 由于观测值y是已知的,即Φ不依赖于y,所以我们可以用Φ(p)表示Φ(p;y)。用B(0,r)⊂U表示圆心在原点和半径r的球,用 ‖ · ‖Σ表示带有权重Σ的欧几里得范数。利用正问题的性质,以下命题保证了参数反演问题的适定性: 后验分布存在,且连续依赖于数据y。 3.2.2 数值结果 观测数据的生成与上一节类似,初始条件均为空间均匀稳态附加一定水平的扰动,参数取值为A=0.58、M=0.45、T=30。实验设定10-5为稳态阈值,即当系统离散时间导数的L2范数小于阈值时,可以认为系统达到了稳态。实验记录了终时T以及T/10、T/5、T/3、2T/3时的数据。为了验证系统解的稳定性,实验还继续求解t=2T时刻的系统解,并检查T时刻和2T时刻解之间的差值是否低于阈值。图8表明,T时刻之后系统已达稳态。 图8 系统解的稳定性Fig.8 Stability of system solution 实验将标准偏差为5%的高斯噪声添加到原始观测数据(见图9(a))中,所得结果如图9(b)(第332页)所示。 图9 添加噪音后的观测结果Fig.9 Observations after adding noise 参数的先验信息是由[0.4,0.7]×[0.5,0.8]区域上的正态分布来建模的。在已知部分先验信息之后,具体地,我们采用马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)抽样算法,进行Metropolis Hastings采样[13],计算模型参数的后验分布。 针对正问题的求解耗时长的问题,本文在实现过程中引入了自适应以及参数迁移的思想: 每次采样模拟记录下拟合表现最好的几对参数,并在下一次模拟中,让模拟点尽可能与之相近,以期更快速地逼近最优参数组。图10展示了次数为100的自适应MCMC采样的样本分布,图11展示了加入随机项后最后10次的采样分布,k模拟为模拟次数。 图10 自适应MCMC采样的样本分布Fig.10 Sample distribution of adaptive MCMC sampling 图11 加入随机项后的采样分布Fig.11 Sampling distribution after adding random items 在图12中可以看到参数对(A,M)的后验分布的95%置信域。仔细观察置信域如何集中在精确值附近,我们会发现这不同于最初的认识——在区域[0.4,0.7]×[0.5,0.8]上服从正态分布。数值实验结果表明,95%置信域被包含在[0.587,0.616]×[0.438,0.458]范围内,并且置信域在A方向的长度大约是M方向的1.5倍。此外,图中信息还表明,可信域中心点距离真实的最优值十分相近,这一定程度上验证了算法的有效性。 图12 参数A和M的后验分布的95%置信域Fig.12 95% confidence region of posterior distribution for parameters A and M 图13给出了基于反演所得参数值对系统进行重构的结果。这些数据图表明,本节算法可以很好地重构植被斑图的演化过程,预测结果与实际相符。 图13 重构植被斑图的结果(上: 真实值,下: 重构值)Fig.13 Results of reconstructing vegetation patch map 本文基于广义Klausmiere-Gray-Scott方程,建立了带有土壤水扩散反馈调节机制的平地植被斑图的演化模型,分别对具有终时观测和间断观测的参数识别问题,应用了不同的反演算法,并在数值实验中验证了算法的有效性。植被呈现斑图状的地区的生态模式具有不稳定性,植被斑图的生成与演化受降水量、植被死亡率等自然因素的制约影响,所以关键参数识别对于植被防护、地理探测具有重要的现实意义。对于已知终时观测的参数识别问题,变步长梯度算法能够有效合理地估计出参数,但算法具有一定的局限性: 不能用来估计与非平稳目标函数相关的参数;如果损失函数中的目标函数没有接近反应扩散系统的解,则算法可能无法收敛,产生不准确的模型参数估计。而现实中,终时观测难以获得,观测往往具有一定的离散特性,需要研究者从中分析系统演化特点,预判系统演化趋势。贝叶斯理论为已知一定先验信息的参数反演问题提供了途径。本文使用马尔可夫链蒙特卡罗(MCMC)抽样方法来确定产生与数据相似模式的反应扩散系统参数的分布,进行了若干次数值模拟,找到了参数的可信域。 由于实际区域的生态组成和观测条件都较复杂,本文做了适当的简化,该模型有待进一步地被细化。植被斑图的演化需要由耦合的非线性扩散反应方程来刻画,再之由于反问题自身的非线性,这为参数识别的提出与理论分析增加了一定的困难。如何给定适当的附加条件保证所提出反问题的适定性,如何建立这类反问题的条件稳定性,这都是值得进一步深入探讨的问题。3.1 终时观测的参数识别问题








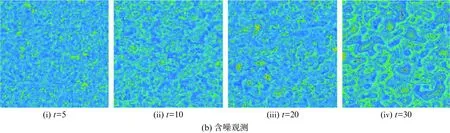
3.2 间断观测的参数识别问题







4 结 语
