吕 芳

(洛阳师范学院 数学科学学院，河南 洛阳 471934)

1 基本概念

定义1[1]设{X(t),t∈T}是一个随机过程，如果对于每一个t∈T，都有E|X(t)|2<∞ ,则称{X(t),t∈T}为二阶矩过程.

定义2[2,.3]设{X(t),t∈T}是一个随机过程，如果对于任意n≥1和任意t1,t2,…,tn∈T，(X(t1),X(t2),…,X(tn))是n维正态随机向量，则称{X(t),t∈T}为正态过程或高斯过程.

将概率空间(Ω,F,P)上具有二阶矩的随机变量的全体记为H.

2 相关定理

定理1[2]若二阶矩过程{f(t,u)X(t),t∈[a,b]}，{g(t,u)Y(t),t∈[a,b]}在[a,b]上都均方可积，则对于任意的常数α,β(不全为零)，{αf(t,u)X(t)+βg(t,u)Y(t),t∈[a,b]}在[a,b]上也均方可积，且

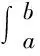
引理2[7]设m维随机向量X=(X1,X2,…,Xm)～N(μ,B)，若n维随机向量Y是X的线性变换，即Y=XC，其中C是m×n阶矩阵，则Y服从n维正态分布N(μC,CTBC).

引理3[5]设{X(t),t∈T}为正态过程，均值函数为mX(t),协方差函数为CX(s,t),则{X(t),t∈T}的任意有限维特征函数为

ri∈R,ti∈T,i=1,2,…n,n∈N.

定理4设{X1(t),t∈T}，{X2(t),t∈T}，…，{Xm(t),t∈T}为m个相互独立的实正态过程，记第i(1≤i≤m)个实正态过程{Xi(t),t∈T}的均值函数为mXi(t)，协方差函数为CXi(s,t),令Z(t)=a1X1(t)+a2X2(t)+…+amXm(t),t∈T，其中a1,a2,…,am是不全为零的实常数，则{Z(t),t∈T}仍为实正态过程，其任意有限维特征函数为

其中ri∈R,ti∈T,i=1,2,…n,n∈N,j2=-1.

证明 1)由于{X1(t),t∈T}，{X2(t),t∈T}，…，{Xm(t),t∈T}均为实正态过程且相互独立，所以∀n≥1，∀t1,t2,…,tn∈T，随机向量

(X1(t1),X1(t2),…,X1(tn))

(X2(t1),X2(t2),…,X2(tn))

⋮

(Xm(t1),Xm(t2),…,Xm(tn))

均服从n维正态分布且这m个向量相互独立，由引理1知随机向量

(X1(t1),X1(t2),…,X1(tn),X2(t1),X2(t2),…,X2(tn),…,Xm(t1),Xm(t2),…,Xm(tn))

服从n×m维正态分布，即随机向量

(X1(t1),X2(t1),…,Xm(t1),X1(t2),X2(t2),…,Xm(t2),…,X1(tn),X2(tn),…,Xm(tn))

服从n×m维正态分布.

(Z(t1),…,Z(tn))=

(a1X1(t1)+a2X2(t1)+…+amXm(t1),…,a1X1(tn)+a2X2(tn)+…+amXm(tn))=

(X1(t1),X2(t1),…,Xm(t1),X1(t2),X2(t2),…,Xm(t2),…,X1(tn),X2(tn),…,Xm(tn))×

由引理2知随机向量(Z(t1),…,Z(tn))服从n维正态分布，故随机过程{Z(t),t∈T}为实正态过程.

2)下面计算实正态过程{Z(t),t∈T}的任意有限维特征函数.

{Z(t),t∈T}的均值函数为

mZ(t)=E(Z(t))=E(a1X1(t)+a2X2(t)+…+amXm(t))=

a1E(X1(t))+a2E(X2(t))+…+amE(Xm(t))=

a1mX1(t)+a2mX2(t)+…+ammXm(t),t∈T

{Z(t),t∈T}的相关函数为

RZ(s,t)=E(Z(s)Z(t))=

E[(a1X1(s)+a2X2(s)+…+amXm(s))(a1X1(t)+a2X2(t)+…+amXm(t))]=

{Z(t),t∈T}的协方差函数为

CZ(s,t)=RZ(s,t)-mZ(s)mZ(t)=

ammXm(s))(a1mX1(t)+a2mX2(t)+…+ammXm(t))]=

由引理3知实正态过程{Z(t),t∈T}的任意有限维特征函数为

其中ri∈R,ti∈T,i=1,2,…n,n∈N,j2=-1.

3 主要结论

定理5设{X1(t),t∈[a,b]}，{X2(t),t∈[a,b]}，…，X{Xm(t),t∈[a,b]}是m个相互独立的实正态过程，记第i(1≤i≤m)个实正态过程{Xi(t),t∈T}的均值函数为mXi(t)，协方差函数为CXi(s,t),设f1(t,u)，f2(t,u)，…，fm(t,u)是m个[a,b]×U上的普通实函数，

{f1(t,u)X1(t),t∈[a,b]}，{f2(t,u)X2(t),t∈[a,b]}，…，{fm(t,u)Xm(t),t∈[a,b]}在[a,b]上都均方可积，令

其中α1,α2,…,αm是不全为零的实常数，则{H(u),u∈U}为实正态过程，其任意有限维特征函数为

其中ri∈R,ui∈U,i=1,2,…n,n∈N,j2=-1.

证明 由定理1知

由定理2知

其中ri∈R,ui∈U,i=1,2,…n,n∈N,j2=-1.

定理得证.