Dongxing LI (李东行)

School of Financial Mathematics and Statistics，Guangdong University of Finance，Guangzhou 510521，China

E-mail:47-075@gduf.edu.cn

Hasi WULAN (乌兰哈斯)

Department of Mathematics，Shantou University，Shantou 515063，China

E-mail:wulan@stu.edu.cn

Ruhan ZHAO (赵如汉)†

Department of Mathematics，SUNY Brockport，Brockport，NY 14420，USA

E-mail:rzhao@brockport.edu

Abstract We give some characterizations of Carleson measures for Dirichlet type spaces by using Hadamard products.We also give a one-box condition for such Carleson measures.

Key words DK space;Hadamard product;mean growth;Carleson measure

1 Introduction

Let D={z∈C:|z|＜1}be the unit disk，let∂D={z∈C:|z|=1}be the unit circle，and let Hol (D) be the space of all analytic functions on D.Fora，z∈D，letbe the Mbius transformation on D that interchangeszanda.It is known that the Green function of D with logarithmic singularity ata∈D is given byg(z，a)

For 0＜p≤∞，the mean growth of functionfon D is defined as

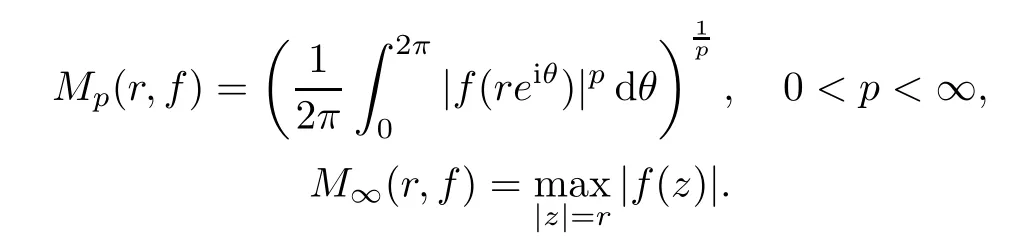
The Hardy spaceHpconsists of those functionsfthat are analytic on D for which

For 0＜p＜∞andα＞-1，the weighted Bergman spaceconsists of thosef∈Hol (D) such that

The weighted Dirichlet space(0＜p＜∞，α＞-1) consists of thosef∈Hol (D) such thatf′∈.Hence，iffis analytic in D，then

The classical Carleson measure was introduced by Carleson[8]in his solution to the corona problem.We say that a positive Borel measureμon D is a Carleson measure if the embedding operator from the Hardy spaceHpintoLp(dμ) is bounded;that is，there is a positive constantCsuch that

for allf∈Hp.There is a simple geometric characterization of these measures.

For an arcI⊂∂D，let|I|denote the normalized arc length ofIso that|∂D|=1.We call

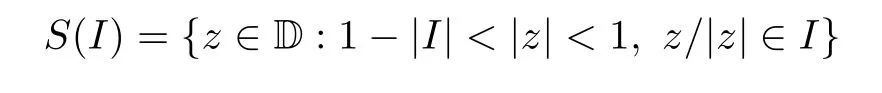
a Carleson box.It is well-known that a positive measureμon D is a Carleson measure if and only if there exists a constantC＞0 such thatμ(S(I))≤C|I|for allI⊂∂D.Ifa=(1-|I|)eiθis the midpoint of the inner side of the Carleson box;we will also denoteIbyIaandS(Ia) byS(a).

We may extend the notion of the Carleson measure by replacing the right-hand side of (1.1) by the norm or the semi-norm of some other function space such as the Bergman space，the Bloch space，or the BMOA，etc..In general，if we letXbe a space of analytic functions on D，for 0＜p＜∞，a positive Borel measureμon D is said to be ap-Carleson measure for the spaceXif the embedding mapI:XLp(dμ) is a bounded operator，i.e.，there is a constantC＞0 such that

for all functionsf∈X.When the parameterp=2，we always simply leave out thepin front of the Carleson measure.The following result is due to Wu:

Proposition 1.1([16]) Suppose that 0＜p≤2，and letμbe a positive Borel measure on D.Thenμis ap-Carleson measure forif and only ifμis a classical Carleson measure.

Ifs＞0 andμis a positive Borel measure on D，we can generalize the classical Carleson measure by saying thatμis ans-Carleson measure on D if there exists a positive constantCsuch thatμ(S(I))≤C|I|sfor any intervalI⊂∂D.Note that the following two notations are different:

(i)μis ap-Carleson measure on D;

(ii)μis ap-Carleson measure for a spaceX.The following results are known:

Proposition 1.2([13]) Assume that 0＜p＜∞，thats＞1，and letμbe a positive Borel measure on D.Thenμis ans-Carleson measure on D if and only ifμis ap-Carleson measure for

Proposition 1.3([15]) Suppose that 0＜s＜∞.Ifμis a Carleson measure forDs，thenμis ans-Carleson measure.In particular，fors≥1，μis a Carleson measure forDsif and only ifμis ans-Carleson measure.Fors=0，ifμis a Carleson measure forD，then

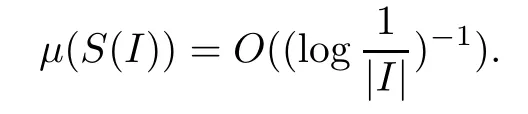
For a right continuous and nondecreasing functionK:[0，∞)[0，∞)，we define the weighted Dirichlet spaceDKof analytic functionsfon D such that

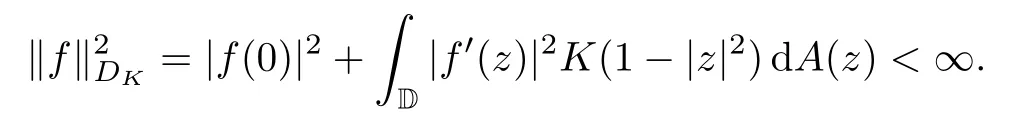
ForK(t)=ts，0＜s＜∞，we have thatDK=Ds.

By Theorem 2.1 in[10]，we may assume thatKis defined on[0，1];we may extend its domain to[0，∞) by settingK(t)=K(1) fort＞1.Furthermore，we need the two following conditions onK:

Note that (1.3) implies the ensuing doubling condition;that is，there exist positive constantsCandMsuch that

Also，by Theorem 5 in[17](see also Theorem 3.8 in[18])，we know that ifKsatisfies condition (1.3)，then

Suppose thatKsatisfies (1.3).Then，we see thatKalso satisfies (1.4) and (1.5).By a proof similar to the one for Theorem 2.18 in[18]，we know that in this case，an analytic functionfon D is inDKif and only if

2 Carleson Measure With Hadamard Products

By Parseval’s formula，(1.6)，and Theorem 6 in[17]，we get

Proposition 2.1Suppose thatKsatisfies (1.2) and (1.3).Thenf∈DKif and only iff*g∈H2，where

Aulaskari，Girela and Wulan gave the following characterization of a Carleson measure by using Hadamard products:

Proposition 2.2([4]) For 0＜s＜∞，a positive Borel measureμdefined on D is a classical Carleson measure if and only if there exists a positive constantCsuch that

One of our goals is to extend these results to thes-Carleson measure and toDKspaces.We need the following result:

Lemma 2.3([9]) Let 0＜s＜∞.A positive Borel measureμon D is ans-Carleson measure if and only if

Theorem 2.4Suppose thatKsatisfies conditions (1.2) and (1.3).A positive Borel measureμon D is ans-Carleson measure fors≥1 if and only if there exists a constantC＞0 such that

Proof“⇒”.Then，by Proposition 2.1，we know that

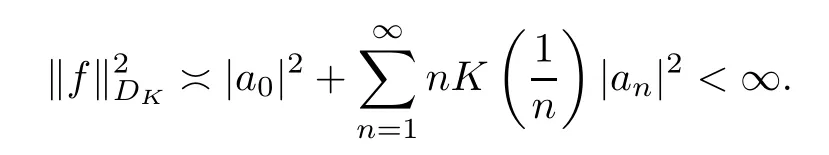
Using this equation and (1.3) of[4]，we get that

is equivalent to

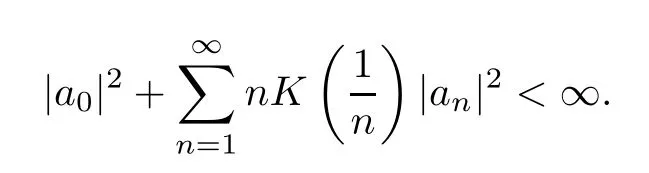
This gives that

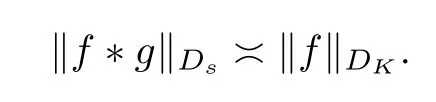
By Theorem 1.2 in[15]we know thatμis ans-Carleson measure withs≥1 if and only ifμis a Carleson measure forDs.Hence，we have that

“⇐”Conversely，suppose that (2.1) holds for allf∈DK.For eacha∈D with|a|＞，we take the testing function

By Proposition 2.1，we have that

Since，forp＞0，we have that

by Stirling’s formula

we get that

On the other hand，

From (2.1) and the inequality，it follows that

By Lemma 2.3，we know thatμis as-Carleson measure. □

Theorem 2.5Suppose thatKsatisfies condition (1.3).A positive Borel measureμon D is ans-Carleson measure fors＞1 if and only if there exists a positive constantCsuch that

Proof“⇒”Suppose thatμis ans-Carleson measure.Let

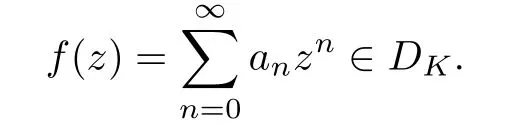
“⇐”Conversely，suppose that (2.3) holds for allf∈DK.For eacha∈D with|a|＞we take the testing function

Therefore，

Combining the above inequalities and (2.3)，we obtain that

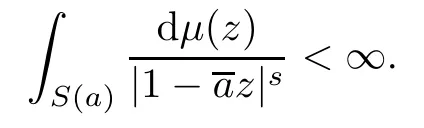
By Lemma 2.3，this means thatμis as-Carleson measure. □

3 One-Box Conditions for Carleson Measures

The classical Carleson one-box conditionμ(S(I))=O(|I|) can be generalized asμ(S(I))=O(φ(|I|)) by providing a nondecreasing functionφ:(0，1]→(0，∞).It is proved in[12]that a finite positive Borel measureμon D is a Carleson measure forDif it satisfies the Carleson one-box condition

whereφ:(0，1](0，∞) is an increasing function such that

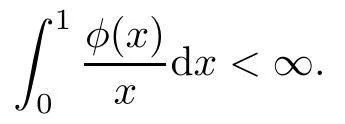
A Hilbert spaceHhas a reproducing kernelkw(z)=k(z，w) in the sense that

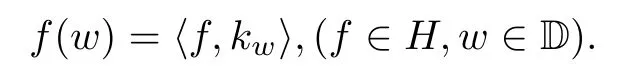
The following result is known:

Proposition 3.1(Lemma 24 of[2]) Assume that a Hilbert spaceHhas a reproducing kernelk(z，w).Letμbe a finite positive Borel measure on D.Then

From this result we immediately obtain the following characterization of a Carleson measure forH:

Corollary 3.2A finite positive Borelμon D is a Carleson measure for Hilbert spaceHwith a reproducing kernelk(z，w) if and only if

By the Cauchy-Schwartz inequality and the fact that|k(z，w)|=|k(w，z)|，we have that

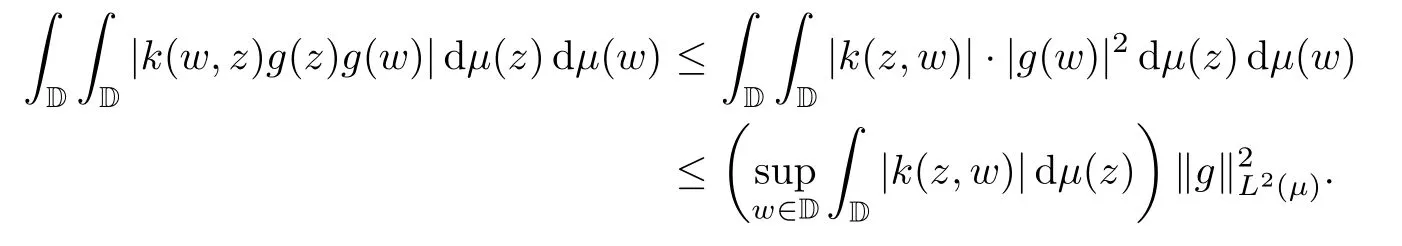
Therefore we get

Corollary 3.3A finite positive Borel measureμon D is a Carleson measure for Hilbert spaceHwith a reproducing kernelk(z，w) provided that

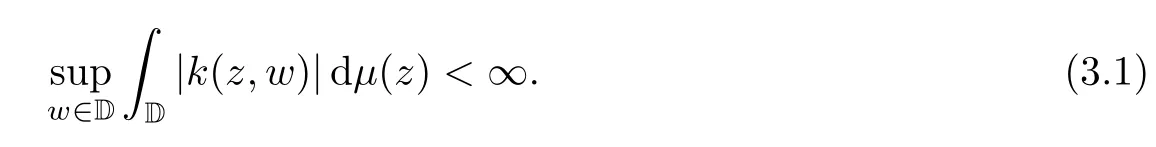
As an extension of a result of[12]，we have the following theorem:

Theorem 3.4Lets＞0，and letμbe a finite positive Borel measure on D satisfyingμ(S(I))=O(φ(|I|))，whereφ:(0，1](0，∞) is an increasing function such that

Thenμis a Carleson measure forDs.

ProofWe mainly follow the proof of Theorem 1.1 of[12].It suffices to show that (3.1) holds.In establishing (3.1)，we can restrict our attention to thosewwith＜|w|＜1，since the supremum over the remainingwis clearly finite.

LetkDs(z，w) be the reproducing kernel forDs.The following estimate is well-known:

see，for example，page 28 in[3].

Fixwwith＜|w|＜1.By (3.3)，using Fubini’s theorem to integrate by parts，we have that

is not void whent＞1-|w|and Ωt=D whent≥1+|w|.Letw=reiθ.By a geometric consideration，we can prove that Ωt⊆S(It)，whereItis the arc on∂D centered ateiθwith normalized arc length

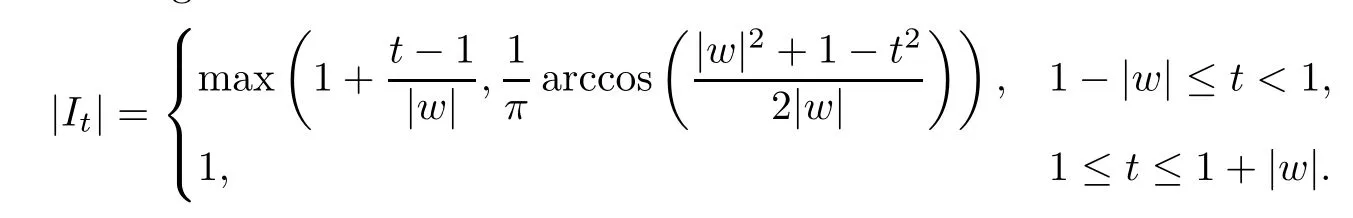
It can be easily shown that for 1-|w|≤t＜1，

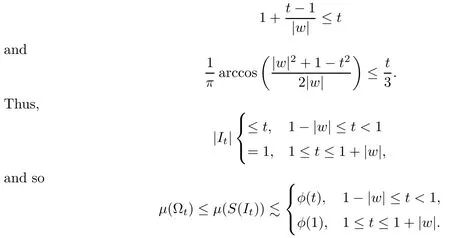
Therefore，by our condition in the theorem，we get that

By Corollary 3.3 we know thatμis a Carleson measure forDs. □

We give two examples here to illustrate this result.The first example gives an application of Theorem 3.4.

Example 3.5Let 0＜s＜1 and letβ＞1.Let.It is proved by Pau and Pel´aez in Lemma 2.1 in[14]that ifμis a finite positive Borel measure on D satisfyingμ(S(I))=O(φ(|I|))，thenμis a Carleson measure forDs.It can be easily checked thatsatisfies condition (3.2).Hence，the above result of Pau and Pel´aez is an easy consequence of Theorem 3.4.

The next result shows that the result in Theorem 3.4 is in some sense sharp.

Example 3.6For any 0＜s＜1，there exists an increasing functionφon (0，1] such thatis strictly decreasing and

and there exists a finite positive Borel measureμon D satisfyingμ(S(I))=O(φ(|I|)) such thatμis not a Carleson measure forDs.

To prove this result，we need the concept ofQsspaces，which was introduced in[5].There are several equivalent definitions ofQsspaces;here we adopt a definition using Carleson measures.

Letting 0＜s＜∞，we say that an analytic functionfon D is in the spaceQsif dμf(z):=|f′(z)|2(1-|z|2)sdA(z) is ans-Carleson measure on D (see Theorem 1.1 in[6]).Relating to this paper，the concept ofQsspaces has been generalized toQKspaces using the weight functionKdiscussed above.Please see[7，19]and[20]for some more information aboutQKspaces and some other generalizations ofQsspaces.

In Corollary 2.1 in[1]，Aleman，Carlsson and Persson proved that for everys∈(0，1)，there exist functionsf∈Qs，g∈Dssuch that

Note that the last condition is equivalent to the fact that the measure dμf(z):=|f′(z)|2(1-|z|2)sdA(z) is not a Carleson measure forDs.

Back to Example 3.6.For any 0＜s＜1，letφ(t)=ts.Then，obviously，φsatisfies all the conditions in Example 3.6.Letfbe the function in Aleman，Carlsson and Persson’s example above，and let

Sincef∈Qs，we know that dμfis ans-Carleson measure，or thatμf(S(I))=O(φ(|I|)) forφ(t)=ts.However，dμfis not a Carleson measure forDs，hence we know that Example 3.6 is true.

Finally，as a corollary to Theorem 3.4，we get the following one-box condition for Carleson measures onDKspaces:

Corollary 3.7Suppose thatKsatisfies condition (1.3).Letμbe a finite positive Borel measure on D satisfyingμ(S(I))=O(φ(|I|))，whereφ:(0，1](0，∞) is an increasing function such that

Thenμis a Carleson measure forDK.

ProofIt is proved in[11，Lemma 2.2]that if (1.3) holds，then there is a weight functionK*，comparable toK，such thatK*(t)/tis decreasing for 0＜t＜∞.Thus，DK=DK*，and since

for 0＜t≤1，we know thatDK⊆D1.By Theorem 3.4，we know thatμis a Carleson measure forD1，and hence also a Carleson measure forDK.The proof is complete. □