m-广义负相依随机阵列的完全q 阶矩收敛性
2022-06-24何其慧
何其慧
随机变量收敛性在统计等诸多领域应用广泛,对其进行研究是概率极限理论研究的热点.在随机变量收敛性中,完全收敛性是一种较强的收敛性质,它不但可以建立随机变量的强大数律,还可以建立随机变量加权和的收敛速度.完全收敛性的概念由文献[1]提出:如果对任意的ε>0,都有

假设{Xn,n≥1} 为一随机变量序列,且an>0,bn>0,q>0.文献[2]引入了下述关于完全矩收敛性的概念:
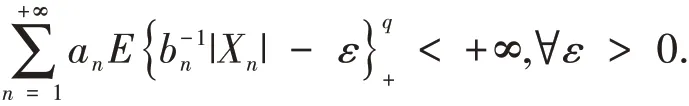
容易验证由完全矩收敛性可推出完全收敛性.因此,完全矩收敛是比完全收敛更强的一种收敛性质,对其进行研究具有十分重要的理论和实际意义.关于完全收敛性和完全矩收敛性的相关研究可参考相关文献[3-11].特别地,文献[8]得到了如下的完全1-阶矩收敛的结果.
定理1 设{Xni,1 ≤i≤kn,n≥1} 为END 随机变量阵列,{cn,n≥1} 为一列正的常数.若下列条件成立:
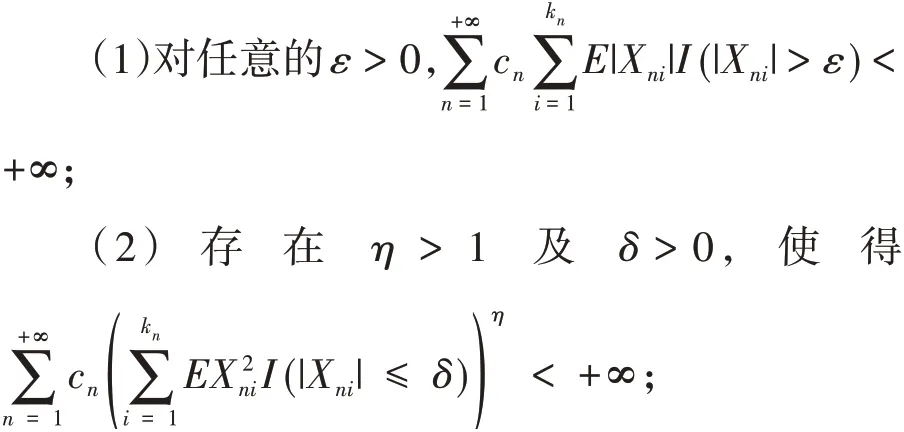

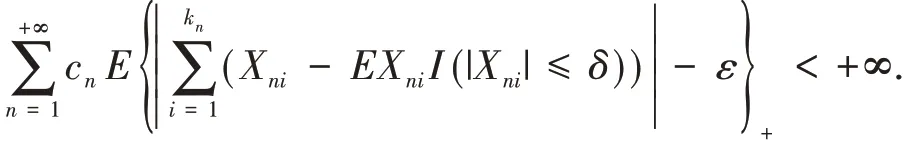
本文一方面将定理1 的结论从完全1-阶矩收敛性改进到完全q阶矩收敛性(q>0),另一方面将{Xni},1 ≤i≤kn,n≥1 从END 随机变量阵列推广到m-END 随机变量阵列,从而得到更好的结果.
文中引用如下一些记号:C表示正的常数,且在不同的地方可以取不同值,I(A)表示事件A的特征函数,a+= max{a,0}.
1 预备知识
首先回顾文献[12]提出的如下关于END随机变量的概念.
定义1 称随机变量阵列{Xn},n≥1 是END 的,如果存在一个常数M>0,使得对任意的n≥1 和所有的实数x1,x2,…,xn,都有

及

文献[13]在END 的基础上提出了如下关于m-END 随机变量的概念.
定义2 令m≥1 为给定的正整数.则随机变量阵列{Xn,n≥1} 被称为m-END 的,如果 对 任 意 的n≥2 及 任 意 的i1,i2,…,in,使 得|ik-ij|≥m,1 ≤k≠j≤n,都有Xi1,Xi2,…,Xin是END 的.
m-END 随机变量包含了END 随机变量作为特例(取m= 1),且易见还包含了一些随机过程如滑动平均过程(MA)等,故m-END是一类非常宽泛的相依结构,在这种相依结构下研究随机变量的极限定理有着较为重要的理论意义和应用价值.
为证明本文的主要结果,还需要下述几个重要引理.
引理1[13]令{Xn,n≥1} 为m-END 随机变量阵列.若{fn(·),n≥1} 为一列单调非降(或非增)的函数,则{fn(Xn),n≥1} 仍然为m-END随机变量阵列.
下述引理是关于END 随机变量的Kolmogorov 指数型不等式,具体可参见文献[14].
引理2[14]设{ }Xn,n≥1 为END 随机变量序 列,EXn= 0 且,则存在一个常数M>0,使得对任意的x>0,y>0 都有

由引理2,可得到如下关于m-END 随机变量的Kolmogorov 指数型不等式.

证明 对给定的m ≥1,总存在正整数k和j,使得n = mk + j.不妨设对一切i >n 都有Xi= 0.因此有,其中由定义2 可知,对每个固定的j,{Xmi+j,1 ≤ i ≤ k}
都是END 随机变量.故由引理2 可得

引理4 设{Xni,1 ≤i ≤kn,n ≥1} 为m-END随机变量阵列,{cn,n ≥1} 为一列正的常数.若下列两个条件成立:
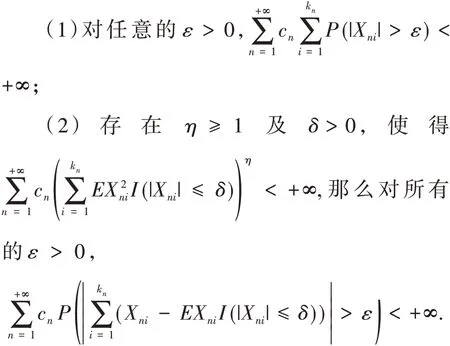
证明 用引理3 替代文献[8]中的引理3.2,可完全类似其定理2.1 的证明得到引理4.
2 主要结果


验证

由条件(1)易知

因此有

由Markov 不等式及条件(3)可得,当n →+∞时,

从而当n 充分大时,对任意的t ≥δq都有
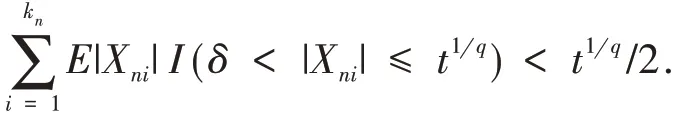
进而
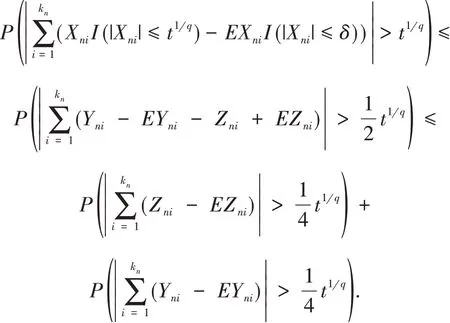
因此,可得
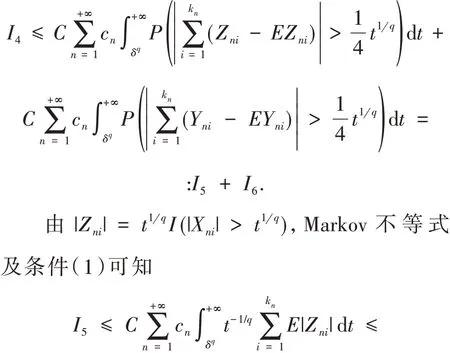
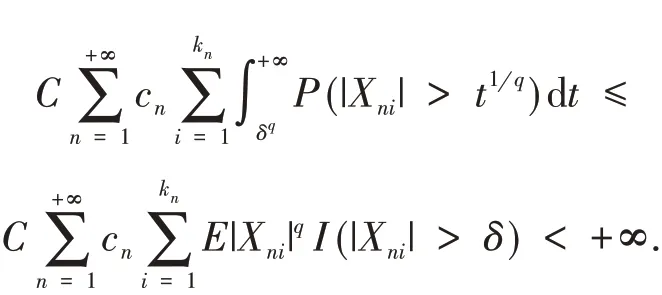
对任意给定的n≥1 及t≥δq,由引理1知,{Yni-EYni,1 ≤i≤kn}仍然是m-END 随机变量阵列. 故在引理3 中取x=t1q/4,y=其 中η>max(1,q),于是可得


而由Cr不等式及Markov 不等式,可得

对于I10,由条件(3)可知,当n充分大时,

于是由条件η>max(1,q)可得
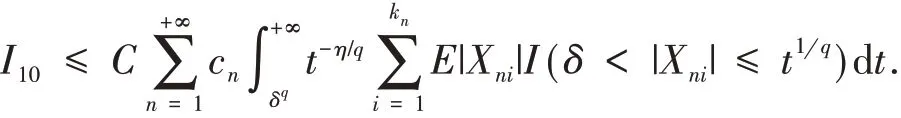
从而若q≥1,则由条件(1)及η>q可得
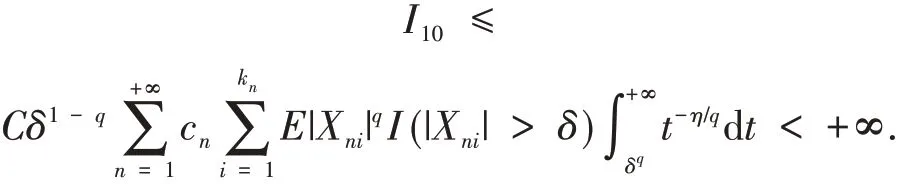
而若0 最后证明I11< +∞.由Markov 不等式及条件(3)可得,当n→+∞时, 即对所有充分大的n,都有 因此由条件(1)可得 注:在定理2 中取q= 1,m= 1,可以看出定理2 与定理1 一致.因此我们的结果将定理1 由END 随机变量阵列的完全1-阶矩收敛改进并推广到了m-END 随机变量阵列的完全q阶矩收敛. 在定理2 的基础上还可进一步得到下述定理. 定理3 设q>0,{Xni,1 ≤i≤kn,n≥1} 为m-END 随机变量阵列,{cn,n≥1} 为一列正的常数.若定理2 中的条件(1)~(3)成立,且存在一个常数,使得当n→+∞时,有 那么对任意的ε>0, 证明 显然定理2 的结论成立.因此,为证明定理3,只需证明当n→+∞时,有 分下述两种情况进行讨论. 情 况1 若δ1≥δ,则 由 条 件(3)和可得,当n→+∞时, 从而定理3 得证. 相依变量的收敛性的研究目前仍是极限理论中的热门问题.本文首先利用m-END 随机变量的定义和性质,从END 随机变量的指数不等式出发,建立了m-END 随机变量的Kolmogorov 型指数不等式. 利用此不等式,进一步得到了m-END 随机变量阵列的完全q阶矩收敛性,此结果是已有文献结果的进一步改进和拓展,具有一定的理论意义和应用价值.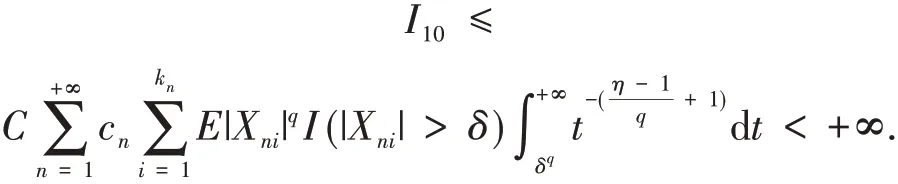
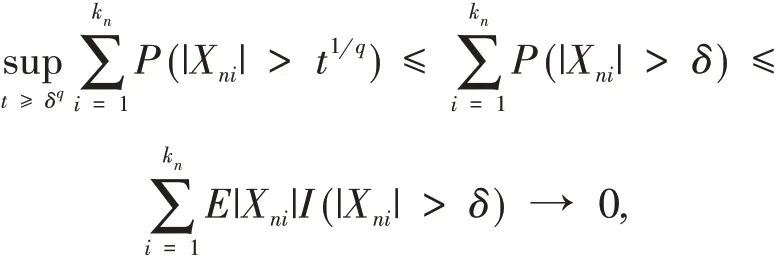
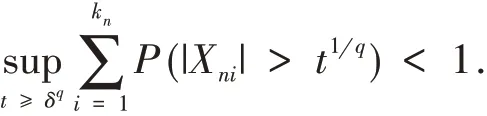

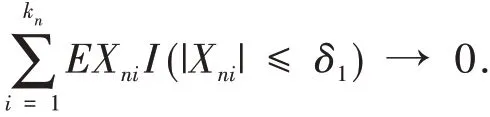
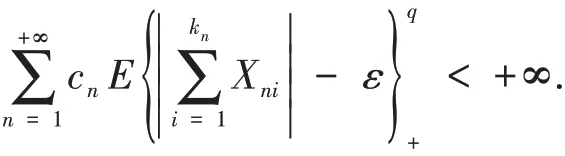




3 结论
