黄建亮 张兵许 陈树辉

(中山大学应用力学与工程系,广州 510275)

引言

增量谐波平衡法(incremental harmonic balance,IHB) 是一个半解析半数值的方法,由Lau 和Cheung[1]于1981 年提出以来,是把增量过程牛顿-拉弗森(Newton-Raphson)迭代过程和谐波平衡过程(伽辽金(Galerkin)平均过程)两者有机地结合起来,已被成功地推广应用于非线性振动的各个领域.Lau[2]和陈树辉[3]分别于1995 年和2007 年对该方法的发展及其应用做了很好的综述.在文献[3-4]中,IHB 法已被总结为具有两大优点:(1)应用于分析强非线性振动问题,并得到高精度解;(2)是一类求解非线性微分方程的计算方法,适用于大范围参数变化的定量分析.

IHB 法已广泛应用在工程中的各个领域,包含航空航天、车辆交通、海洋工程、机械等各种非线性振动问题的分析中[5-8].Wang 和Zhu[9]建立了非圆链轮的汽车皮带传动系统的动力学模型,用IHB法研究减小凸轮轴角度变化的效果.Mitra 等[10]利用IHB 法分析了强非线性半潜式平台系统的主谐波响应和高阶次谐波响应.在机械振动中,齿轮的振动被广泛研究,Li 等[11]分析了具有动态齿隙的齿轮副系统在内外周期激励下的非线性动力学特性;Zhou 等[12]基于IHB 法分析了考虑齿隙、阻尼、传动误差和啮合刚度的直齿圆柱齿轮副动力学模型,发现了跳跃不连续现象和多个稳定解共存.IHB 法对各种动力学问题具有良好的求解效果.Wang 等[13]将非线性波传播问题的控制方程转换为相应的具有多个时滞的非线性时滞微分方程,并应用IHB 法进行计算,大大简化推导的过程和计算的时间.Cheng 等[14]应用IHB 法分析了附加恒力对准零刚度隔振器的主共振和1/3 次谐波共振的影响.Li 和Chen[15]利用IHB 法研究了空气压缩机模型的周期运动,混沌运动和分岔行为.Karličić等[16]利用IHB 法分析了基于马蒂厄-达芬(Mathieu-Duffing)非线性振子模型的非线性压电能量采集器的稳态响应.Shen 等[17]用IHB 法研究了马蒂厄-达芬振子的分岔和混沌路径,识别出了一系列振子的倍周期分岔点,发现它们近似服从普适标度律.IHB 法也被应用于分数阶非线性方程的计算过程中,Shen 等[18]将IHB 法应用到分数阶非线性振子的动力学分析中,建立了该振子周期解的一般形式来获得高精度的解.对于振动系统里含有多个不可约频率的准周期运动问题,Huang 等[19-21]将IHB 法发展成为多时间尺度IHB 法,应用于求解含边频带的准周期运动,自动跟踪非线性系统的准周期运动频率响应.窦苏广等[22]和苏鸾鸣和叶敏[23]将IHB 法应用于非线性系统参数识别,分析了在周期、分岔和混沌等复杂运动状态下的参数识别,并验证了IHB 法相对于其他方法有明显的抗噪性能.此外,他们还将增量谐波平衡非线性识别理论运用到实验建模方法中[24-25].

为了提高IHB 法适应性,人们对它进行了各种改进,主要集中在两个方面.第一方面是要提高IHB 法的计算效率.Wang 和Zhu[26]对非线性代数方程的余项使用快速傅里叶变换逼近,非线性代数方程的雅可比矩阵使用Broyden 拟牛顿迭代方法逼近,从而提高了谐波平衡过程的收敛速度;第二方面是解决系统响应曲线在峰值(或拐点)处的自动跟踪问题.为了可使IHB 法能更好的追踪响应随参数变化情况,特别是在峰值(或拐点)处自动跟踪,避免出现迭代不收敛的问题,可利用弧长延拓法对IHB 法进行改进[4,26-27].另外,Zheng 等[28]在线性增量过程中引入Tikhonov 正则化来解决迭代中的不适定问题,从而改变IHB 法的收敛性能.然而对IHB 法的各种改进,没有涉及到如何选择初值条件的问题,在给定的初值条件有时并不能保证IHB 法的收敛性.

在IHB 法的牛顿-拉弗森迭代过程中,初值可以任意设定,实际上IHB 法的牛顿-拉弗森迭代过程相当于对初值进行多次尝试,并不能保证初值的收敛与否,当迭代的误差增大时相当于换一个初值进行重新迭代尝试.本文针对这一问题,引入回溯线搜索(backtracking line search,BLS)优化算法[29]来调节IHB 法的收敛步长,使步长逐渐减小直至满足弱沃尔夫(Wolfe)条件,即下降性条件,来对初值进行迭代计算.在此基础上,引入迭代负梯度方向,再利用迭代优化算法狗腿法(dogleg method)[30]的思想,加快其收敛速度,提高了初值尝试的局部收敛范围,从而提高了IHB 法牛顿-拉弗森迭代的收敛性.

1 传统的增量谐波平衡法

考虑一个一般形式的n维非线性振动系统,可表示为如下平衡微分方程

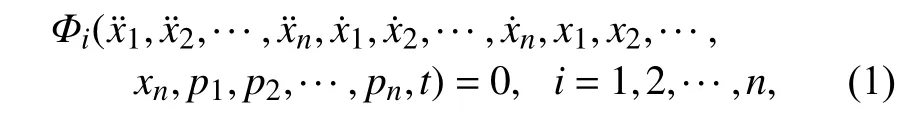
其中,“·”表示对时间t的微分,xi(t) 是位移变量,pi表示第i个外激励,Φi是二阶的非线性常微分方程.引入新的时间变量 τ,定义为

其中,ω 为系统的振动响应频率.方程(1)可表示为

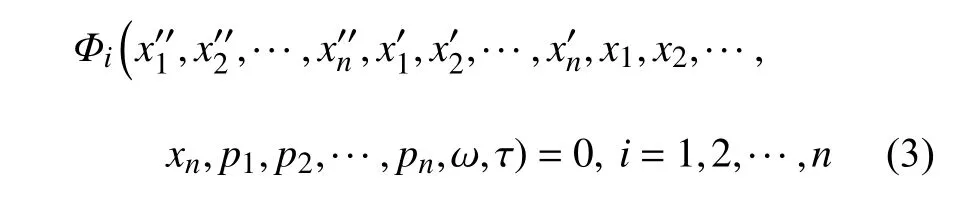
其中,“ ′ ”表示对时间 τ 的微分.

IHB 法的第一步是增量过程,即牛顿-拉弗森迭代过程.设xi0,pi0和 ω0是方程(3)的解,则其邻近解可用增量形式表示为

其中,Δxi,Δpi和Δ ω 为增量.把方程(4) 代入方程(3),并略去 Δxi,Δpi和 Δ ω 的高阶小量,得到了线性化的增量方程

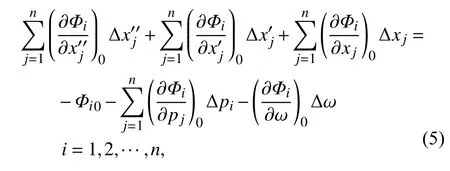
其中,下标0 表示为函数增量的初值.方程(5)可表示为矩阵形式

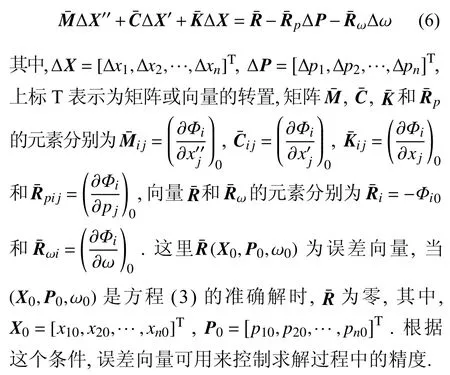
IHB 法的第二步是谐波平衡过程,即伽辽金平均过程.将n维非线性系统的稳态解及其增量都展开成傅里叶级数

其中,nc和ns是正整数,表示谐波项项数;Cs,Ai和ΔAi分别表示为

那么向量X0及其增量可分别表示为傅里叶系数向量A及其增量ΔA

积分上式并整理归并为以 ΔA,Δ ω 和 ΔP为未知量的代数方程组

这里,KA和Rp是nt×nt的矩阵,R和Rω是nt×1 的列向量,nt=n×(nc+ns) .当要分析某一固定外激励幅值下的频率响应曲线时,在方程(14)中取P为固定值,即 ΔP=0,那么方程(14)变成

当要分析某一固定外激励频率下的各响应幅值随外激励幅值变化的响应曲线时,在方程(14)中取ω为固定值,即 Δ ω=0,那么方程(14)变成

在用传统的IHB 法对方程式(19)或式(20)的求解过程中,要给定一个假定的初值,然后可先利用谐波平衡过程再利用增量过程,或也可先利用增量过程再利用谐波平衡过程,追踪出所有的解.在增量过程中,可应用频率增量,振幅增量,或弧长增量,具体可参见文献[3-4].

如上所述,在用传统IHB 法求解过程中,事先要给定一假定的初值,因此涉及到给定初值的选取问题.一般说来,当碰到这类问题时,一般是用三种途径来解决:(1)凭IHB 法使用者的经验,事先给定一接近于精确解作为IHB 法的初值;(2)以线性化系统得到的解作为IHB 法的初值;(3)利用摄动法等求得小参数范围内的弱非线性振动的解作为IHB 法的初值.在传统IHB 法用牛顿-拉弗森迭代过程中,如给定的初值在通往收敛的路径上,那么解就会收敛至精确解,即此初值点是在其收敛范围内.为了扩大初值点的选择范围,在用牛顿-拉弗森迭代过程中,本文将对迭代的增量进行两个方面的改进.

2 引入BLS 优化算法的改进增量谐波平衡法(GIHB1)

其中,向量KAk和Rk分别表示KA和R在第k次迭代的结果.

现对传统IHB 法中的迭代增量进行改进.首先,引入目标函数

当 ‖R‖→0 时,f(A)→0 .再引入一次函数和基于Cauchy-Point 的二次函数

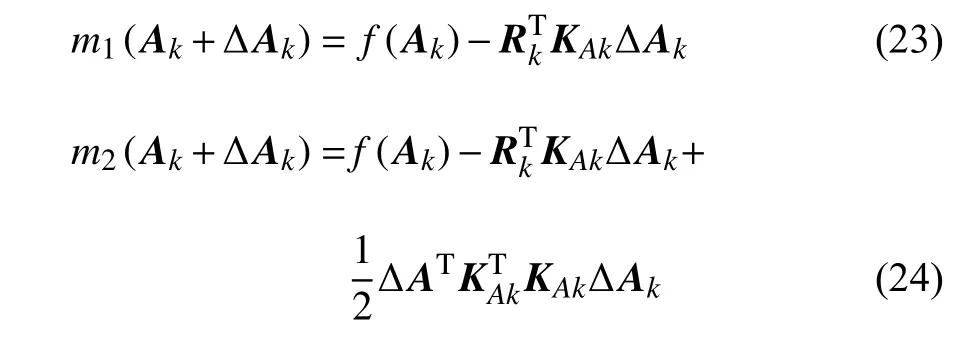
其中,向量Ak表示A在第k次迭代的结果.

当初值选择恰当时,‖ ΔA‖ 越小,对f(Ak+ΔAk)在点Ak上进行模拟,m2(Ak+ΔAk) 与f(Ak+ΔAk) 的差越小.在迭代过程中,用m2(Ak+ΔAk) 代替f(Ak+ΔAk)进行求解,则增量变为

当KAk为非奇异矩阵时,等价于原牛顿-拉弗森迭代增量式(21),即使得迭代一步就到达m2(Ak+ΔAk)最小点.

当初值选择不当时,可导致 ‖ ΔA‖ 较大,m2(Ak+ΔAk) 代替f(Ak+ΔAk) 吻合度较差,因此导致f(Ak+ΔAk) 的值不降反增,从而导致迭代不收敛.对此,引入BLS 优化算法将其迭代步长进行改进,以为牛顿-拉弗森迭代方向,由于

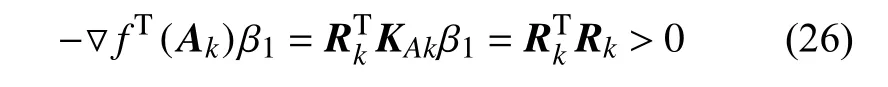
因此牛顿-拉弗森迭代的方向 β1与负梯度方向呈锐角,满足方向下降条件.在 β1前乘以系数 α ,当α较小时,满足弱Wolfe 条件时

即可选定迭代步长,然后再进行IHB 法的第二步谐波平衡过程(Galerkin procedure),其中,常数c通常较小,一般可取c=1.0×10-4,该优化算法的迭代过程如图1 所示.在图1 的算法中,为了保证较快的迭代速度,取 α =1 为牛顿-拉弗森迭代的初值,ρ在每次迭代时与 α 相乘,为了保证步α β1逐渐减小,取 0 ＜ρ ＜1 .随着迭代次数的增加,α 值逐渐减小,即A的增量 α β1逐渐减小,直至满足弱Wolfe 条件,然后跳出循环,以得到Ak为初值,重新执行牛顿-拉弗森迭代过程.

图1 结合Backtracking line search (BLS)优化算法的IHB 法(GIHB1)Fig.1 Algorithm for a generalized IHB method with backtracking line search (BLS) method (GIHB1)

3 引入狗腿法思想并结合BLS 算法的改进IHB 法(GIHB2)

为了加快BLS 算法的迭代运算速度,应用狗腿法的思想,在此过程中加入两个调节参数用于控制迭代方向.当 ‖ ΔA‖ 较小时,为负梯度方向,即最快的下降方向.m2(Ak+ΔAk) 在 β2方向上的最小值对应的系数 αmin可由

系数 αmin的主要作用是调节负梯度方向的步长,使得该步长和模拟函数牛顿-拉弗森迭代的步长处于同一个量级.在狗腿法思想基础上,引入两个调节参数 α1和 α2用于加快BLS 算法的迭代运算速度.令Ψ1k=α1αminβ2,Ψ2k=β1,其中,α1是调节目标函数f(Ak) 和二次模拟函数m2(Ak+ΔAk) 的迭代方向,α1∈(0,0.1) .当 ΔA沿 着 0 →Ψ1k→Ψ2k方向时,m2(Ak+ΔAk) 逐 渐下降到最小值,其中 0 表示为零向量.

引入函数

用于调节迭代的方向,其中,α2起线性化分割的作用,其值可取 α2∈(0,0.1) .同时,引入m2(Ak+ΔAk)与f(Ak+ΔAk) 的拟合系数 ρk,可表示为

此系数 ρk越大时,m2(Ak+ΔAk) 与f(Ak+ΔAk)的吻合程序越高,f(Ak+ΔAk) 越满足下降条件.算法的迭代过程可利用系数 ρk值的大小来判断 α 是否满足条件.对于系数 ρk界定一个阈值 ρ0,当 ρk＞ρ0时,系数 α 满足条件;否则继续减小,直至满足ρk＞ρ0,该算法的迭代过程如图2 所示.

在图2 所示的算法中,α =1 时迭代方式为牛顿-拉弗森迭代,α 与F(α) 的模长有正相关的关系.随着迭代次数的增加,α 值逐渐减小,即A的增量F(α) 的模长逐渐减小,直至 ρk＞ρ0,然后跳出循环,得到初值Ak,然后重新执行牛顿-拉弗森迭代过程.

图2 结合BLS 算法和狗腿算法的改进IHB 法(GIHB2),其中在狗腿算法的函数 F (α) 中引入2 个调节参数 α 1 和α2Fig.2 Algorithm for a generalized IHB method (GIHB2) combined with BLS method and dogleg method that contains two parametersα1 and α2 in the functionF(α)

值得注意的是上述两种改进的IHB 法随着 α 的减小,迭代效率会逐渐降低,当 α ＜10-6时,即认为迭代不收敛.为了提高收敛性的同时,提高迭代的效率,在算法实现过程中,可设 α 的下界值为0 .01,若α ＜0.01 ,则令Ak+1=Ak+0.1β1改变初值,重新执行算法的迭代过程.

4 算例

利用3 种IHB 法,即传统的IHB 法、结合BLS 算法的GIHB1 法和引入狗腿思想并结合BLS 算法的GIHB2 法,对两个算例的初值问题进行分析,一个是经典的单自由度范德波尔(van der Pol)振荡,另一个是耦合的两自由度范德波尔振荡.在IHB 法的求解过程中,此二类范德波尔振荡的极限环周期解依赖于给定的初值条件.为了检验上述3 种IHB 法计算结果的准确性,本文采用四阶龙格-库塔(Runge-Kutta,RK)数值法作为比较.四阶R-K数值法是直接对微分方程采用时间积分法,它可以较准确地给出系统某一时刻的位移、速度和加速度的数值.

4.1 van der Pol 振荡

单自由度van der Pol 振荡方程为

其中,“·”表示对间t的导数,参数 λ 在区间 [ 0,1.0] 内取值用来分析系统响应的霍普夫分岔.当单自由度van der Pol 振荡方程(32)中的2 个参数 ε 和 λ 确定时,该振荡方程具有唯一一个极限环.这类van der Pol 振荡方程在航空航天、力学以及电子等工程领域都有很广泛的应用.例如,Motta 和Malzacher[31]发展了湍流经过机翼面的van der Pol 模型,根据此模型构建了开环与闭环的流量控制.Akhtar 等[32]提出了水动力作用在圆柱/椭圆柱结构上的范德波尔-达芬振荡模型,用此模型得到的计算结果与CFD 的结果一致.Facchinetti 等[33]基于van der Pol 振荡方程研究了在涡振中结构与波的耦合振荡.

值得注意的是,经典摄动法只能适用于 ε 为小参数时van der Pol 振荡方程的求解,而不适用于大参数时的求解.Burton[34]说明了当 ε ＞1.0 时,利用摄动法去求解会得到错误的结果.而IHB 法的优势是不仅适用于弱非线性系统,也适用于强非线性系统,不失一般性,文中 ε 可取大参数作为分析.

引入新的时间变量

方程(33)变为

其中,“ ′ ”表示为时间变量 τ 的导数.

因方程(34)只含奇次项,系统是对称的振荡响应,可将x展开为含有m个奇次谐波项的傅里叶级数

根据式(14),得

其中,KA是 2m×2m的矩阵,对应于傅里叶系数向量

向量R和Rω可分别由式(16)和式(17)计算得到.在本文中取误差向量R的模 ‖R‖ 小于1 .0×10-7作为IHB 法谐波平衡过程的收敛条件.

显然,式(36)中所含的未知量的数目比方程的数目多2 个,由于系统响应频率 ω 是未知的,因此必须选定 Δ λ 为主动增量,再选定式(37)中的某一谐波项系数为参考量,如b1,那么该参考量的增量为零,即 Δb1=0,这样方程(36)就可求解.具体步骤可参见文献[3-37]等.

现利用上述3 种方法分别对van der Pol 振荡方程(32)求解,其中,λ =0.87 ,ε =5.0 ,选定b1为参考量.同时,在式(35)中取谐波项项数为m=25 .图3所示为在取不同初值时用3 种方法得到的误差‖R‖与迭代次数的关系.从图中可以得到:

(1)图3(a)中选定初值为频率 ω0=0.58,谐波项系数a1=1.0 ,b1=1.0,其余谐波项系数设为零,可以看出传统的IHB 无法收敛,另外两种改进方法均可收敛,GIHB1 法经25 步迭代达到‖R‖＜1.0×10-7的收敛条件,GIHB2 法经23 步迭代达到收敛条件,其响应频率为 ω =0.5877 ;

图3 不同初值条件下用3 种IHB 法求解van der Pol 振荡方程(32)迭代收敛情况,其中,ε =5.0 ,λ =0.87 .初值分别为:(a) ω 0=0.58 ,a 1=1.0 ,b 1=1.0 ;(b) ω 0=0.58,a 1=1.0,b 1=1.4 ;(c) ω 0=0.58,a 1=1.8,b1=-0.7Fig.3 Iteration convergence of solution of van der Pol Eq.(32) with different initial values using the three IHB methods,where ε =5.0,λ=0.87 .Initial values are (a) ω 0=0.58 ,a 1=1.0 ,b 1=1.0 ;(b) ω 0=0.58 ,a 1=1.0,b 1=1.4 ;(c) ω 0=0.58 ,a 1=1.8,b1=-0.7

(2)图3(b)中选定初值为频率 ω0=0.58,谐波项系数a1=1.0 ,b1=1.4,其余谐波项系数设为零,可以看出三种方法都可收敛,传统IHB 法误差 ‖R‖ 先增大再减少,其最大值可达到3113,然后开始下降,在误差增大过程中,增量的模长较大,易出现跳出牛顿-拉弗森迭代的现象,导致整个迭代不收敛.而对改进后的两种方法来说,误差 ‖R‖ 可一直保持减少,直至满足迭代条件.可以看出传统IHB 法需要28 步迭代达到收敛条件,而改进后的两种GIHB 法分别只需要25 步和15 步迭代达到收敛条件;

(3)图3(c)中选定初值为频率 ω0=0.58,谐波项系数a1=1.8 ,b1=-0.7,其余谐波项系数设为零,可以看出传统IHB 法无法收敛,两种改进GIHB 法均可收敛,GIHB1 法经214 步迭代才能达到收敛条件,而GIHB2 法只需58 步迭代即可达到收敛条件.

图4 所示为用3 种IHB 法求解van der Pol 振荡方程(32) 的初值a1和b1的选定范围,其他初值为ω0=0.58 及谐波项系数除值a1和b1外都为零.可以看出,两种改进后的方法其初值的选定范围一样,且均多于传统IHB 法的初值选定范围.图5 所示为取λ=0.87,ε =5.0 时van der Pol 振荡方程(32)的极限环,可以看出3 种IHB 法求出的结果是一致的,是因为两种改进的GIHB 法只涉及到增量过程的改进,而谐波平衡过程没有改变;同时3 种IHB 法求得的结果与用四阶R-K 法求得的数值结果高度吻合.

图4 用3 种IHB 法求得van der Pol 振荡方程(32)解的初值 a1 和b1的选定范围,其他初值为 ω 0=0.58 及其他谐波项系数设为零Fig.4 The regions for the initial value for a1 and b1 of solutions of van der Pol Eq.(32) using the three IHB methods,the other initial value for frequncy is ω 0=0.58 and the other initial harmonic terms are set to be zero

图5 用3 种IHB 法和四阶龙格-库塔数值法求得范德波尔振荡方程(32)的解,其中 λ =0.87 和ε=5.0Fig.5 Solutions of van der Pol Eq.(32) by the three IHB methods and numerical integration using the fourth-order R-K method,where λ=0.87 andε=5.0

4.2 耦合van der Pol 振荡

众多学者对工程中出现的耦合van der Pol 振荡的动力学特性感兴趣.Barron 和Sen[35]考虑了在一质量-弹簧结构上4 个耦合van der Pol 振荡的同步性.Siewe 等[36]从实验上分析了在非线性与时滞耦合的两个van der Pol 振荡的同步性,实验得到的结果与理论分析相一致.现考察两自由度耦合van der Pol 振荡方程[37-38]

其 中,μ1=-0.1 ,μ2=0.5 ,γ1=0.1 ,γ2=0.08 .同样 利用IHB 法求解这类强非线性耦合振荡系统,引入新的时间变量 τ =ωt,方程变为

因方程(39)只含有奇次项,系统是对称的振荡响应,可将x1和x2展开为含有m个奇次谐波项的傅里叶级数

其中,m=10 .根据式(14),同样可得方程(36),其中,KA是 4m×4m的矩阵,对应于傅里叶系数向量

同样选定 Δ λ 为主动增量,再选定式(41)中的谐波项系数b11为参考量,那么该参考量的增量为零,即 Δb11=0 ,根据方程(36)即可得在不同参数 λ 下系统响应的频率 ω ,即 λ -ω 响应曲线.在此例中,给定不同的初值,利用IHB 法会得到不同的 λ -ω 响应曲线.设选定初值为ω0=1.0

其中,l为取1 的个数,m-l表示取0 的个数.图6 表示耦合van der Pol 振荡方程(38)在其系数 μ1=-0.1,μ2=0.5,γ1=0.1 和 γ2=0.08 ,初值条件为 ω0=1.0 和式(42)下,3 种IHB 法计算所得的系统频率 ω 与参数 λ 的对应关系曲线(ω -λ),在这些曲线上的每一点就对应系统的一个极限环.在图6 中,3 种IHB 法都可求得系统响应频率 ω ≈1.0 附近的 ω -λ 关系曲线,两种改进的GIHB 法可求得系统响应频率ω ≈0.67 和ω ≈0.3 附近的的ω -λ 关系曲线,而结合狗腿法和BLS 算法的GIHB2 法还可求得系统响应频率 ω ≈0.4 和 ω ≈0.2 附近的的 ω -λ 关系曲线.表明了两种改进后的GIHB 法相比传统的IHB 法有更广的初值选定范围,得到了传统IHB 法较难求得的解,特别是结合狗腿法和BLS 算法的GIHB2 法可以得到系统解的全貌.值得一提的是:进一步研究表明,在 ω ≈1.0 附近的 ω -λ 关系曲线有一半的点对应的极限环是稳定的,另一半对应的极限环是不稳定的;其余4 条曲线对应的极限环也是不稳定的.

图6 不同初值条件下用3 种IHB 法求得耦合范德波尔振荡方程(38)的解,其中,μ 1=-0.1 ,μ 2=0.5 ,γ 1=0.1 和γ2=0.08Fig.6 The solutions of coupled van der Pol Eq.(38) with different initial values using the three IHB methods,where μ 1=-0.1 ,μ 2=0.5,γ1=0.1 ,andγ2=0.08

图7 所示为不同初值条件下用3 种IHB 法求解耦合van der Pol 振荡方程(38)在 ω ≈1.0 附近迭代收敛情况,其中,λ =0.08 ,μ1=-0.1,μ2=0.5 ,γ1=0.1和 γ2=0.08 .图7(a)中选定初值为频率 ω0=1.0,谐波项系数取式(42)中的l=7 ,b11=0.7,可以看出三种方法都可收敛,传统IHB 法误差 ‖R‖ 在前10 迭代过程中在 [ 0,100] 间波动,然后开始下降,达到收敛条件.用两种改进的GIHB 法得到的误差 ‖R‖ 一直减少,直至满足迭代条件.看出传统IHB 法需要18 步迭代达到收敛条件,而两种改进的GIHB 法分别只需要12 步和10 步迭代达到收敛条件.图7(b)中选定初值为频率 ω0=1.0 ,谐波项系数取式(42)中的l=8,b11=0.8,可以看出传统IHB 法在迭代的前10 步过程中波动,第11 步误差徒然变大,之后迭代不收敛.而两种改进的GIHB 法得到的误差 ‖R‖ 一直减少,直至满足迭代条件.改进后的GIHB1 法和GIHB2 法分别只需要14 步和11 步迭代达到收敛条件.图8所示为取λ =0.08 ,μ1=-0.1 ,μ2=0.5 ,γ1=0.1 和γ2=0.08时耦合van der Pol 振荡方程(38)的极限环,可以看出3 种IHB 法求得的结果一致,并与用四阶R-K 法求得的数值结果高度吻合.

图7 不同初值条件下用3 种IHB 法求解耦合van der Pol 振荡方程(38)在 ω ≈1.0 附近迭代收敛情况,其中,λ =0.08 ,μ 1=-0.1,μ2=0.5,γ 1=0.1 和γ2=0.08Fig.7 Iteration convergence of solution of coupled van der Pol Eq.(38)near ω ≈1.0 with different initial values using the three IHB methods,where λ =0.08 ,μ 1=-0.1 ,μ 2=0.5 ,γ 1=0.1 ,andγ2=0.08

图8 用3 种IHB 法和四阶龙格-库塔数值法求得耦合van der Pol 振荡方程(38)的解,其中,λ =0.08 ,μ 1=-0.1 ,μ 2=0.5 ,γ 1=0.1 和γ2=0.08Fig.8 Solutions of coupled van der Pol Eq.(38) by the three IHB methods and numerical integration using the fourth-order R-K method,where λ =0.08 ,μ 1=-0.1 ,μ 2=0.5 ,γ 1=0.1,and γ2=0.08

5 结论

针对传统IHB 法遇到的初值选择问题,本文提出了两种改进的IHB 法,第一种是引入BLS 优化算法的改进IHB 法(GIHB1),其目的是为了调节IHB 法的迭代步长;第二种是在第一种改进的基础上再结合狗腿法思想的改进IHB 法(GIHB2),其目的是为了调节迭代方式,使迭代方向沿着较快的下降方向,从而加快BLS 算法的迭代运算速度.两个自治系统的算例说明了两种改进IHB 法的有效性,第一算例表明两种改进的IHB 法的初值选择范围远大于传统IHB 法的初值选择范围,且GIHB2 法在一些情况下求得解的收敛步数远少于GIHB1 法;第二个算例表明在给定的初值条件下,传统的IHB 法只能得到1 条 ω -λ 关系曲线,GIHB1 法可以得到3 条ω-λ关系曲线,而结合狗腿法思想的GIHB2 法可以得到5 条 ω -λ 关系曲线,同样地,GIHB2 法求得解的收敛步数也小于GIHB1 法.另外,两种改进的GIHB 法只是改进了增量过程,而没有改变谐波平衡过程,计算的结果与传统IHB 的结果是一致的,所以两种改进的GIHB 法对于非自治系统的分析也是有效的.综上,引入BLS 优化算法再结合狗腿法思想的GIHB2 法在解决初值问题上是传统IHB 法的有效补充,可进一步推广至高维非线性振动系统上.