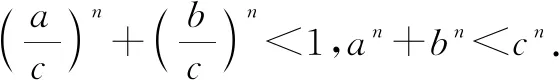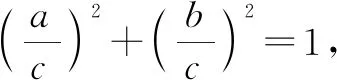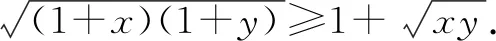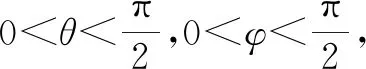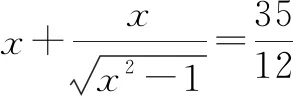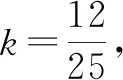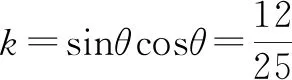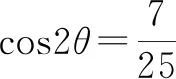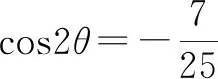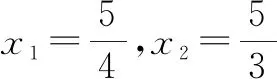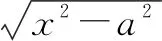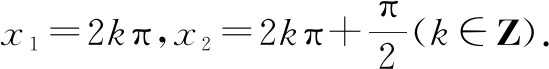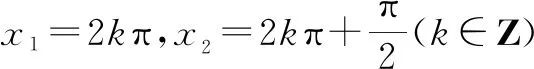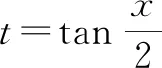⦿山东省泰安第二中学 刘延群

1 引言

在解数学题时，我们可以把某个代数式看成一个新的未知数(元)来实行变量替换，从而使问题得到简化，这种方法就是换元法.换元法的实质是转化，转化是为了达到“化繁为简、化难为易、化陌生为熟悉”的目的[1].换元法的关键是构造元和设元，它的基本思路就是等量代换.在高中数学中，我们常用换元法将分式转化为整式、将无理式转化为有理式、将高次式降幂、将超越式转化为代数式.

具体来说，采用换元解题有以下六种常见的方法.

2 比值换元法

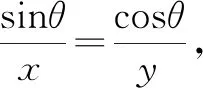
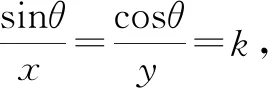
由 sin2θ+cos2θ=1(三角公式)，得

即3x4+3y4-10x2y2=0.

再由因式分解，化简为(3x2-y2)(x2-3y2)=0.

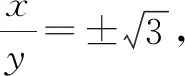
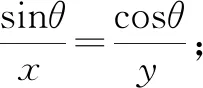
3 整体换元法

例2设x是实数，求证：(x2+4x+5)(x2+4x+2)+2x2+8x≥-10.

证明：令y=x2+4x+2.

易知y=(x+2)2-2≥-2，ymin=-2.

则(x2+4x+5)(x2+4x+2)+2x2+8x

=(y+3)y+2y-4=y2+5y-4

根据f(y)的单调性及ymin=-2可知，fmin(y)=f(-2)=(-2)2+5(-2)-4=-10.

故原不等式成立.

方法与技巧：整体换元的思路，就是通过对整体问题的观察，研究整体结构的特性，从而导出局部结构和元素的特性.这里的“整体”和“局部”是相对而言的，例如本题中的令y=x2+4x+2 就只是相对的“整体”，因为相对于整个待证式来说它又是“局部”，其优势就在于其繁琐的原式左边能用这个“局部”很简捷地表示出来，从而使证明过程变得简单明了.

4 倒数换元法

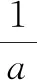
例3解方程：4x4-8x3+3x2-8x+4=0.

解：因为x≠0，可用x2除方程的两边，得

①

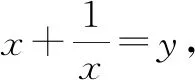
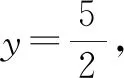
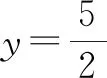
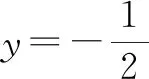
5 均值换元法

例4在复数集上解方程：(x+1)6+(x+2)6+(x+3)6=2.

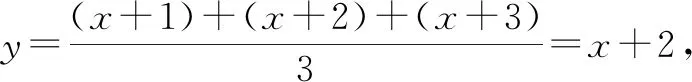
展开整理,得y2(y4+10y2+10)=0.

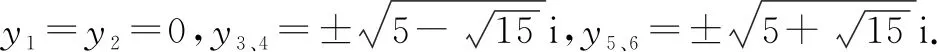
方法与技巧：本题若将方程直接展开得六次方程，不仅繁琐而且不容易解出，所以应该采用均值换元法.均值换元的实质是根据二次展开式(x+a)n+(x-a)n可消去含a的奇次项，且利用这些特征将某些高次方程转化为特殊的高次方程以便于求解.这种均值换元法还可以推广到更多项的这类特殊高次方程.

6 对称置换法

例5求函数y=sinxcosx+sinx+cosx的最大值.

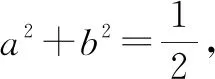
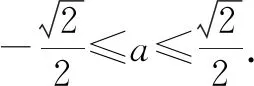
则y=(a+b)(a-b)+(a+b)+(a-b)

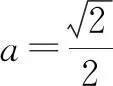
方法与技巧：本题如果直接将sinx用cosx表示，则带根式；若用万能公式则又会出现高次幂，都比较繁琐.所以我们可以根据题目的特点，采用对称换元后很快就能将其可转化为一元二次函数的最值问题[2]，达到了化难为易的目的.

7 三角换元法

例6已知a2+b2=c2(a,b,c∈R+)，求证：an+bn2且n∈N).

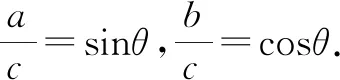
因为a,b,c∈R+，于是0

又因n-2为大于1的自然数，所以

因此，sinnθ+cosnθ

又因为 1≥cos(θ-φ),所以

①

令sinθcosθ=k，则(sinθ+cosθ)2=1+2k.

代入①式得： 144(1+2k)=1 225k2，

1 225k2-288k-144=0.

例9解方程：sinx+cosx+sinxcosx-1.

整理化简,得 2t(1-t)(t2+t+2)=0.

解得t=0，t=1.

即

由此可见，在一个比较复杂的数学式子中，当直接解答有困难时，我们可以考虑用新的变元去代替原式的一个部分或改造原来的式子，这样能使运算简化，使问题易于解决.