吉 蕾

(晋中学院 数学系，山西 晋中 030619)

0 引言

考虑如下一类椭圆系统

(1)

其中：Ω⊂RN(N≥5)是具有光滑边界∂Ω的有界开集，参数k≥0.

系统(1)源自文献[1]建立的数学模型.自此，四阶椭圆型方程得到了人们广泛的关注研究，近期相关结果可参见文献[2-6]等及其相关文献.文献[7]研究了系统(1)在一维情形下解的存在性.在非线性项形式更一般时，文献[8]运用山路引理和强极大值原理得到了系统(1)的正解.山路引理的运用需要假设(AR)条件，但在实际应用中，有很多函数不满足(AR)条件.文献[9]中作者提出了非二次条件.因此，本文考虑了非二次条件下系统(1)正解的存在性.

1 预备知识

下面给出本文所用的一些符号和定义，以及用到的命题.

设λ1是问题

-Δu=λu，x∈Ω，u=0，x∈∂Ω

Δ2u=λu，x∈Ω，Δu=u=0，x∈∂Ω

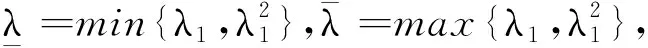
由变分法知，系统(1)的弱解对应于以下能量泛函的临界点：

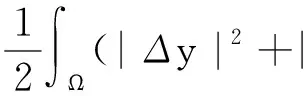
其中：u=(y,z)∈V；F(x,u)为系统(1)的位势函数，即

∇uF(x,u)=f(x,u)=(f1(x,u),f2(x,u)).

且对∀u=(y,z)，v=(ξ,η)∈V，

下面给出泛函J满足(C)c条件的定义及证明中用到的环绕定理：

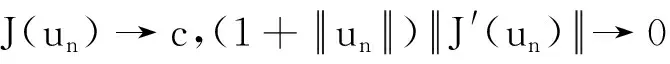
环绕定理[11]设H是实Hilbert空间，泛函J∈C1(H,R)，对∀c>0，满足(C)c条件.若存在闭子集S⊂H和Hilbert流形Q⊂H，且满足：

(ii)S与∂Q环绕；

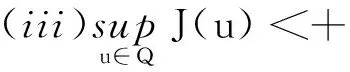
则泛函J有临界值c≥β.

2 主要结果

定理1假设系统(1)满足条件(H1)-(H5)：

(H1)f1，f2∈C(Ω×R2,R).当x∈Ω，u=(y,z)∈R2时，f1(x,u)，f2(x,u)≥0.

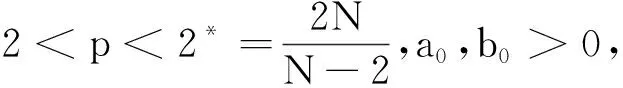
|f1(x,u)|+|f2(x,u)|≤a0|u|p-1+b0.

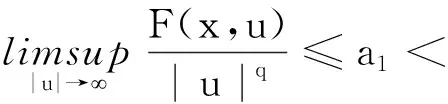
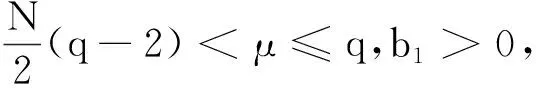
(H5)存在a2，b2>0，使得

关于a.e.x∈Ω一致成立.

则系统(1)至少有一个正解.

推论假设(H1)～(H4)成立，且

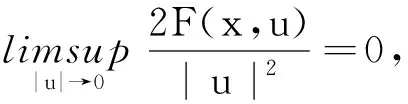
关于a.e.x∈Ω一致成立，则系统(1)至少有一个正解.

注定理中的条件(H4)即为非二次条件.比较上述结果和文献[8]中的定理，文献[8]中的条件(H3)即为(AR)条件，容易找到满足推论条件而不满足(AR)条件的函数，例如

F(x,u)=|u|2ln(1+|u|2).

3 主要结果的证明

分三步完成定理的证明.

第一步 证明对∀c∈R，泛函J满足(C)c条件.

由条件(H2)，上述泛函J∈C1(V,R)，设c∈R，任取{un=(yn,zn)}⊂V且

(2)

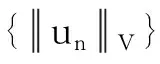
由(2)可得，存在M>0，使得

(3)

又由条件(H4)，存在实数M1>0，当|u|≥M1时，有

(4)

当|u|0，使得

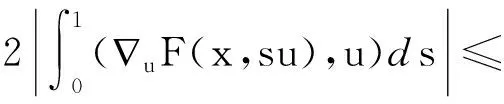
(5)

由(4)、(5)可知存在常数C2>0，使得对∀u∈R2和a.e.x∈Ω，有

成立.因此由(3)可推知

(6)

由条件(H3)，存在常数M2>0，使得当|u|≥M2时，有

当|u|0，使得F(x,u)≤C4.对∀u∈R2和a.e.x∈Ω，有

F(x,u)≤2a1|u|q+C4.

(7)

一方面，由(3)和(7)可得

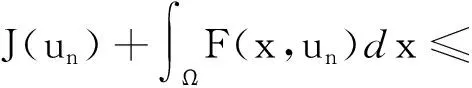
(8)

另一方面，当k≥0时，

(9)

因此由(8)、(9)可得

(10)

于是，将Hölder不等式、Sobolev嵌入不等式和式(6)应用于式(10)，可得

(11)

其中C6>0为常数.

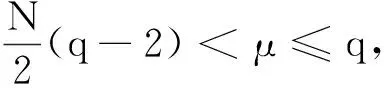
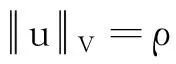
事实上，令

则

对ε0>0，由(H2)和(H5)可知，存在A≥0，B≥0，使得对∀u∈R2和a.e.x∈Ω，

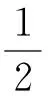
(12)

成立.所以

其中

又由(12)有

所以

(13)

令u0=(φ1,φ1)，则

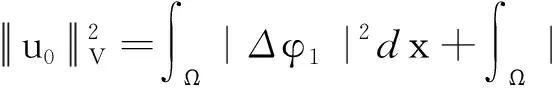
(14)

由(13)和(14)可得，当t→∞时，

第三步 证明泛函J存在非零临界点，并证明该非零临界点为系统(1)的正解.

应用环绕定理，令

其中t0>0，使得J(t0u0)≤0.因此泛函J存在临界值c≥γ>0，设J(u*)=c>0，则J′(u*)=0，即u*为泛函J的非零临界点，即为系统(1)在V中的非零弱解.设u*=(y*,z*)，根据(H1)可断言：y*≥0且z*≥0.

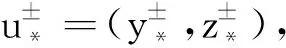
由k≥0得

由定理的结论，很容易推得推论成立.

4 结语

本文通过环绕定理和强极大值原理，当非线性项在无穷远处满足非二次条件时，得到了椭圆系统(1)正解的存在性. 此时非线性项更具一般性，所得结论推广了相关文献的内容.