付昌建 耿圣飞 刘品

(1.四川大学数学学院,成都,610064;2.西南交通大学数学学院,成都,611756)

1 引言

为了给代数群的全正性和量子群的典范基建立一个组合的研究框架,Fomin 和Zelevinsky[1]于2002 年左右引入了丛代数.随着研究的深入,人们在不同数学分支中发现了丛代数结构,使得丛代数得到广泛的关注并成为一个重要且热门的研究分支.这些数学分支包括但不限于离散动力系统、Poisson 几何、几何不变量理论、高维Teichmüller 理论以及代数表示论等[2-10].丛代数与这些不同数学分支之间的联系不同程度地刺激了各个数学分支自身理论的发展,同时反过来也为研究丛代数提供了新的工具和方法.一个典型的例子是代数表示论中的丛倾斜理论[8],它产生于丛代数的刺激,是经典倾斜理论的延续.同时,丛倾斜理论又为一大类丛代数的研究提供了加法范畴化[11],使得人们能够借助代数表示论中的方法解决丛代数中的诸多猜想[12].

丛代数具有丰富的组合结构,它是由一些称为丛变量的元素生成的交换代数,这些丛变量按某种规则构成固定势的称为丛的集合.生成元由一个初始给定的丛通过递归的方式给出,而递归的信息由一个可斜对称化的整数矩阵给出.本文将从丛代数的定义出发,回顾丛代数中出现的几类整数向量:c-向量、d-向量、f-向量和g-向量,介绍它们的定义、性质和它们在丛代数的结构理论中所发挥的重要作用,以及与之相关的研究问题和最新的研究进展.

本文结构如下:第2 节从矩阵突变的概念出发回顾丛代数的基本定义并介绍丛代数中的洛朗现象定理、正性猜想以及有限型丛代数的分类定理.第3 节介绍丛代数中的分母向量(d-向量)和分母猜想以及最新的研究进展.第4 节回顾主系数丛代数的相关理论.特别地,介绍c-向量、g-向量和f-向量的定义和相关的性质.第5 节首先回顾丛代数中的分离公式,该公式分别建立了丛变量和g-向量与F-多项式的精确关系以及系数变量和c-向量与F-多项式的精确关系.然后将c-向量、g-向量和f-向量推广至一般的丛代数并综述相关的研究进展.

2 丛代数的基本概念

本节回顾丛代数的基本概念和重要结论.主要参考文献为[1,13].

设P 是一个乘法阿贝尔群,如果其上还存在加法运算⊕且与乘法运算有分配律,那么称P 为一个半域(semifield).设z1,...,zl是l个不定元,Trop(z1,...,zl)表示z1,...,zl的所有Laurent 单项式全体.显然Trop(z1,...,zl)在多项式的乘法“·”下构成一个乘法阿贝尔群.令

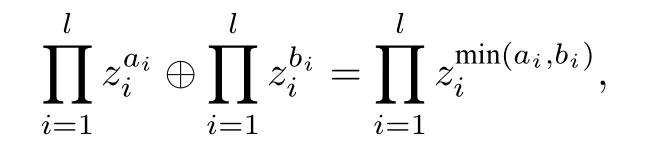
则(Trop(z1,...,zl),·,⊕)为半域,称为不定元z1,...,zl的tropical 半域.Tropical 半域在丛代数理论中起着重要作用.

固定正整数n和半域P.记ZP 为乘法群P 的整系数群环,Q(P)为ZP 的分式域.用F表示系数为Q(P)的n个不定元的多项式环的分式域,用[1,n]表示集合{1,...,n}.对于一个整数a,记[a]+=max(a,0).若α=(a1,...,an)T∈Zn,则记

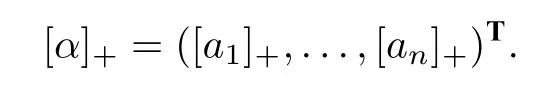
类似地,若β=(b1,...,bn)T∈Zn,则记

以Mn(Z)表示所有n阶整数方阵构成的集合.如无特别说明,本文中出现的矩阵都是n阶方阵.

2.1 矩阵突变

设B ∈Mn(Z).如果存在对角元为正整数的对角矩阵S=diag{d1,...,dn}使得SB为斜对称的(即(SB)T=-SB),那么称B为可斜对称化的,称矩阵S为B的可斜对称化子.

定义1设B=(bij)∈Mn(Z) 为可斜对称化矩阵,k ∈[1,n].定义矩阵μk(B)=()∈Mn(Z),其中

称μk(B)为矩阵B沿方向k的突变.

容易验证,μk(B) 仍是可斜对称化的且与矩阵B有相同的可斜对称化子.因此可以对矩阵μk(B) 应用沿任意l ∈[1,n] 方向的突变μl得到矩阵μl ◦μk(B).直接验算可知(B) :=μk ◦μk(B)=B,即沿同一方向的突变为对合.

定义2设B=(bij)∈Mn(Z)是可斜对称化矩阵.如果不存在指标序列1≤i1,i2,...,il ≤n使得那么称矩阵B为无环的(acyclic).两个可斜对称化矩阵B1和B2如果满足:存在一系列指标i1,...,ir ∈[1,n],使得

那么称B1和B2是突变等价的.

对于可斜对称化矩阵,有如下两个基本问题.

问题1给出一个有效的方法判断两个给定的可斜对称化矩阵是否突变等价.

问题2给出一个有效的算法判断一个给定的可斜对称化矩阵是否突变等价于一个无环的矩阵.

当n=2 时,问题1和问题2 都是平凡的.除此之外,仅对n=3 情形有肯定的回答,参见文献[14-16].

2.2 种子突变

定义3称三元组(x,y,B)为域F中的一个(系数属于P 的)带标记的种子,如果(x,y,B)满足如下条件：

(1) x=(x1,...,xn)的分量之集为域F的一个自由生成子集,即x1,...,xn是Q(P)代数无关的,且包含x1,...,xn的最小的域为F;

(2) y=(y1,...,yn)为P 中的n-元组;

(3)B ∈Mn(Z)为可斜对称化矩阵.

称x 为种子(x,y,B) 的丛(cluster),矩阵B为种子(x,y,B) 的交换矩阵(exchange matrix),元素x1,...,xn为丛变量(cluster variables),y1,...,yn为系数变量(coefficients).

矩阵突变可以自然地推广到种子突变,它是丛代数中最本质的定义.

定义4设(x,y,B) 为F中的一个系数属于P 的带标记的种子,k ∈[1,n],其中x=(x1,...,xn),y=(y1,...,yn),B=(bij)∈Mn(Z).定义三元组μk(x,y,B) :=(x′,y′,B′),其中

(1) 矩阵B′=μk(B),即B′为矩阵B沿方向k的突变;

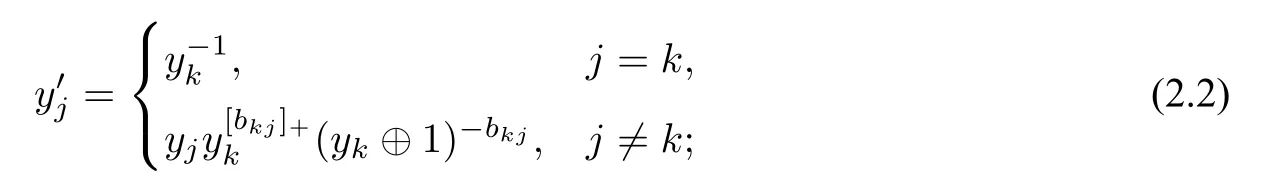
称μk(x,y,B)为种子(x,y,B)沿k方向的突变,(xk,)为一个交换对(exchange pair).

显然,三元组μk(x,y,B)仍是F中的一个系数属于P 的带标记的种子.同样可以考虑种子μk(x,y,B)沿任意l ∈[1,n]方向的种子突变,与矩阵突变类似,仍然有(x,y,B)=(x,y,B).

注1设P=Trop(z1,...,zl),则P 中的元素z为z1,...,zl的Laurent 单项式.此时P 中的n元组w=(w1,...,wn)与l×n-型整数矩阵Cw一一对应.特别地,若,i ∈[1,n],则Cw=(cij).此时种子突变中的系数变量突变公式(2.2)可由矩阵突变公式(2.1)统一给出.

注2设P 为平凡半域,即P={1}.一个系数属于P 的带标记的种子可由二元组(x,B)表示,此时也称种子(x,B)具有平凡系数.

2.3 丛模式

以Tn表示n-正则树.当n ＞1 时,它是平面上的一个具有无限多顶点的连通图,每个顶点恰有n条边与之相连,并且这n条边恰被集合[1,n]中的数标记.

例1当n=2 时,T2的顶点可以由整数集合Z 参数化,进而T2有如下形式:

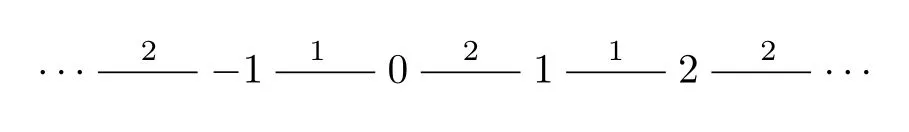
定义5设(x,y,B)为一个系数属于P 的带标记的种子.赋予Tn的每个顶点t一个带标记的种子Σt=(xt,yt,Bt).如果映射Σt满足下述条件

(2) 存在顶点t0∈Tn使得=(x,y,B),那么称映射Σt为种子(x,y,B)的丛模式(cluster pattern/seed pattern).

显然,一个丛模式Σt由t0(x,y,B)唯一确定.因此称顶点t0为该丛模式的根,为初始种子.

2.4 丛代数及洛朗现象

设(x,y,B)为一个系数属于P 的带标记的种子.固定(x,y,B)的一个丛模式Σt使得t0为其根.对每一个顶点t ∈Tn,记

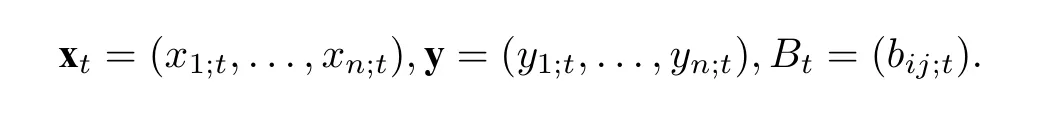
定义6记A:=A()为由所有的丛变量X:={xi;t |i ∈[1,n],t ∈Tn}生成的F的ZP-子代数.称A为丛模式Σt的丛代数,n为A的秩.若P=Trop(u1,...,ul),则称A为几何型丛代数.若A的交换矩阵B为斜对称的,则称A为斜对称型丛代数.如果存在t ∈Tn使得Bt是无环的,那么称A为无环的,此时也称丛xt为无环的.

在同构意义下,丛代数A()由任意一个顶点t ∈Tn处的种子唯一决定.

设s ∈Tn.对任意的t ∈Tn及j ∈[1,n],由交换关系(2.3) 知,丛变量xj;t可以表示为x1;s,...,xn;s的有理函数.事实上,Fomin 和Zelevinsky[1]证明了如下的洛朗现象定理.

定理1([1,定理3.1])对任意的顶点s,t ∈Tn及j ∈[1,n],有

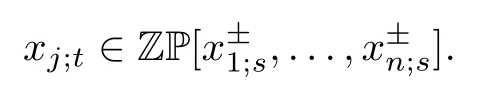
进一步,若P=Trop(u1,...,ul),则

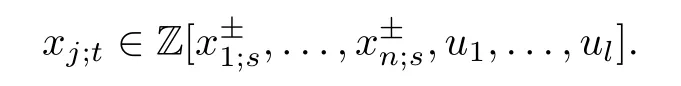
Fomin 和Zelevinsky 在文献[1]的第三节进一步猜测定理1 中的系数总是非负的(称为正性猜想).当交换矩阵B为反对称矩阵时,Lee 和Schiffler[17]利用组合方法证明了正性猜想.最近,Gross等[18]利用丛散射图和组合构造在一般情形下给出了正性猜想的肯定回答.

定理2([18,定理0.3])对任意的顶点s,t ∈Tn及j ∈[1,n],有

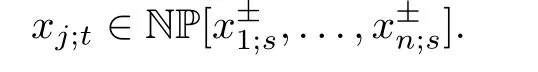
2.5 有限型丛代数的分类

设(x,y,B)为系数属于P 的带标记的种子.固定(x,y,B)的一个丛模式Σt使得t0为其根.

定义7如果集合X:={xi;t |i ∈[1,n],t ∈Tn}是有限集,即A(Σt0)只有有限多个丛变量,那么称丛代数A()为有限型.

Fomin 和Zelevinsky[19]证明了丛代数是否为有限型只与交换矩阵B有关,而与系数P 的选择无关.为了叙述这一结果,我们需回顾可斜对称化矩阵的相伴Cartan 矩阵.关于(广义)Cartan 矩阵的定义和分类,参见文献[20].

设B=(bij)∈Mn(Z)是可斜对称化矩阵.定义A(B):=(aij)∈Mn(Z),其中

显然,A(B)是一个广义Cartan 矩阵.称A(B)为矩阵B的相伴Cartan 矩阵.

Fomin 和Zelevinsky[19]给出了有限型丛代数分类定理.

定理3([19,定理1.4])丛代数A()为有限型当且仅当存在t ∈Tn使得矩阵Bt的相伴Cartan 矩阵为有限型Cartan 矩阵.

根据有限型Cartan 矩阵的分类,有限型丛代数被分类为Al(l ≥1)-型、Bl(l ≥2)-型、Cl(l ≥3)-型、Dl(l ≥4)-型、El(l=6,7,8)-型、F4-型和G2-型.易知,有限型丛代数都是无环丛代数,但并非每个丛都是无环的.

3 分母向量与分母猜想

设(x,y,B)为系数属于P 的带标记的种子.固定(x,y,B)的一个丛模式Σt使得t0为其根.

3.1 分母向量

称由同一个丛的丛变量生成的单项式为丛单项式.设s ∈Tn,根据定理1,任意丛单项式M可以唯一地表示为

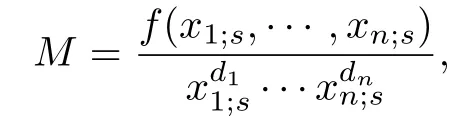
其中d1,...,dn ∈Z,f(x1;s,···,xn;s)∈ZP[x1;s,···,xn;s] 且满足对任意的i ∈[1,n],xi;s∤f(x1;s,···,xn;s).

定义8称向量dens(M) :=(d1,...,dn)T∈Zn为丛单项式M关于丛xs的分母向量(denominator vector),简称为d-向量.

显然,向量dens(M)依赖于顶点s ∈Tn的选取.最近,曹培根和李方[21]利用定理2 及丛散射图证明了Fomin 和Zelevinsky[13]关于分母向量的如下猜想.

定理4([21,定理11])固定顶点s ∈Tn,记[xs]为丛xs中的丛变量构成的集合,z为某个丛变量.

(a) 若z/∈[xs],则dens(z)∈Nn;

(b) 向量dens(z)的第k个分量只依赖于丛变量z和xk;s,而不依赖具体包含xk;s的某个丛;

(c) 向量dens(z)的第k个分量为零当且仅当存在一个丛xt使得z和xk;s同时属于[xt].

Fomin 和Zelevinsky[22]猜测所有的丛单项式是线性无关的.Cerulli Irelli 等[23]对斜对称型丛代数利用表示理论证明了该猜想.最近,该猜想在一般情形下被Gross 等[18]完全解决.曹培根和李方[21]利用定理2 和定理4(a)给出了丛单项式线性无关的一个新证明.作为定理4 的另一个应用,他们利用d-向量定义了丛变量对上的d-相容性函数,推广了Fomin 和Zelevinsky[19]关于有限型根系上的经典相容性函数.需要指出的是,d-相容性函数不再具有经典相容性函数的所有性质(参见[24]).

3.2 分母猜想

分母向量引入的初衷是为了参数化丛单项式.特别地,Fomin 和Zelevinsky[22,猜想4.17][13,猜想7.6]提出了如下的分母猜想.

猜想1(分母猜想)设s ∈Tn,则不同的丛单项式有不同的关于丛xs的分母向量.特别地,同一个丛的丛变量的分母向量构成Qn的一个基.

猜想1 的研究进展是缓慢的,对有限型丛代数都未完全验证是否成立.目前仅对秩为2 和3 的丛代数有肯定的回答.特别地,Sherman 和Zelevinksy[25]利用Kac-Moody 代数的根系对秩为2 的丛代数验证了分母猜想.Lee 等[26]利用丛变量的Newton 多面体对秩为3 的丛代数验证了分母猜想.此外猜想1 对于无环丛代数且取定的丛xs也是无环的情形成立(参见[12,27]).对于一般的丛代数的分母向量,目前未能找到一个类似于秩为2 或者无环丛代数的合适解释.

注意到丛变量是特殊的丛单项式,人们进而考虑分母猜想的一个弱形式.

猜想2(弱分母猜想)设s ∈Tn,则不同的丛变量有不同的关于丛xs的分母向量.

猜想2 可以看作代数表示论中一个经典问题的类比,即对于一个给定的有限维代数,什么样的不可分解模在同构意义下由其维数向量唯一决定? 遗憾的是人们对猜想2 也知之甚少.除前述的情形外,耿圣飞与彭联刚[28]利用代数表示论的方法对斜对称有限型丛代数验证了猜想2 成立.Nakanishi 和Stella[29]利用组合的方法验证了猜想2 对所有的有限型丛代数都成立.

如果存在t ∈Tn使得Bt是无环的且Bt的相伴Cartan 矩阵是仿射型广义Cartan 矩阵,那么称丛代数A()为仿射型丛代数.付昌建和耿圣飞[30]利用代数表示论的方法验证了猜想2 对斜对称仿射型丛代数成立.另一方面,对A,B 或C 型丛代数,分母猜想的如下弱形式成立.

定理5 ([31,定理1.2])设A为A,B 或C 型丛代数且xs为任意的丛,则对任意的丛z=(z1,...,zn),向量dens(z1),...,dens(zn)构成Qn的基.

4 主系数丛代数

本节考虑一类特殊的几何型丛代数:主系数丛代数(cluster algebras with principal coefficients).主系数丛代数在丛代数的结构理论中发挥着本质的作用.设y1,...,yn为形式变量.本节总是假定P=Trop(y1,...,yn).设(x,y,B)为一个系数属于P 的种子.固定(x,y,B)的一个丛模式Σt使得t0为其根.记x==(x1,...,xn),B==(bij).

定义9如果yt0=(y1,...,yn),那么称丛代数A()在顶点t0处有主系数.为了强调在顶点t0处有主系数,记A()为A·(;t0).

在本节中,总是假定A()为主系数丛代数且在t0处有主系数.本节主要参考文献[13].

4.1 c-向量

定义10若对任意的t ∈Tn,存在整数cji;t,j ∈[1,n],使得则称向量ci;t=(c1i;t,...,cni;t)T∈Zn为在顶点t处的第i个c-向量,矩阵Ct=(c1;t,...,cn;t)∈Mn(Z)为在顶点t处的C-矩阵.

注3(1) 由注1 可知,C-矩阵和c-向量也可由如下的递归方式定义:

· 令=In;

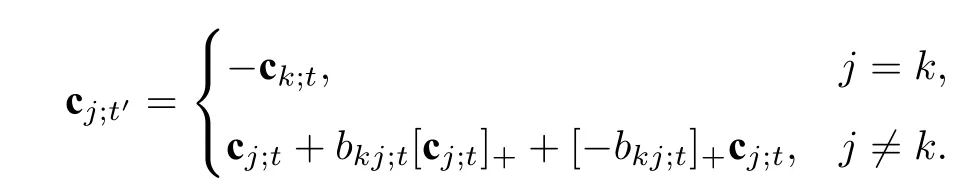
(2) 利用(1)可以将c-向量的定义推广至任意系数的丛代数.显然,该定义依赖于根t0和t0处的交换矩阵B,因此,也将ci;t和Ct分别记为

设α=(a1,...,an)T,β=(b1,...,bn)T∈Zn.若对任意的i ∈[1,n],ai ≥bi,则记α ≥β.进一步,若至少还存在一个j ∈[1,n]使得aj ＞bj,则记α ＞β.显然,“≥”是Zn上的一个偏序.

定义11设α ∈Zn.如果α ＞0 或者α ＜0,那么称向量α具有符号一致性.若α ＞0,则称α是正向量;若α ＜0,则称α为负向量.

Fomin 和Zelevinsky[13]猜测任意的c-向量都有符号一致性(称为c-向量的符号一致性猜想).Derksen 等[32]利用带势箭图的表示在交换矩阵为斜对称矩阵的情形下证明了c-向量的符号一致性猜想.随后,Plamondon[33],Nagao[5],付昌建[34]在此情形下分别给出了不同的证明.最近Gross等[18]在一般情形下完全解决了该猜想.

定理6([18,推论5.5])对任意的t ∈Tn,矩阵Ct在整数上可逆且其列向量有符号一致性.

4.2 g-向量

由定理1 知,对任意的t ∈Tn及j ∈[1,n],

注4(1) 类似于c-向量,g-向量也可由如下的递归方式定义:

· 令=In;

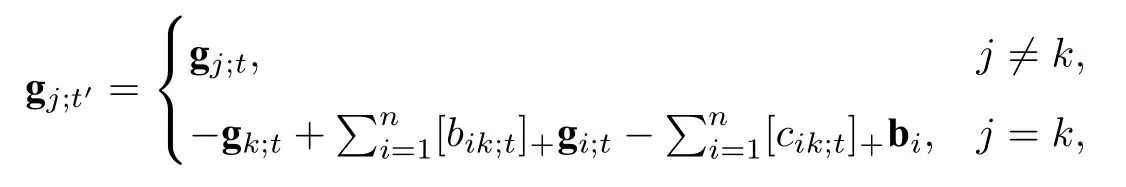
(2) 利用(1),也可以将g-向量和G-矩阵的定义推广至一般系数的丛代数.此时,为了强调它们与根t0及t0处的交换矩阵B的关系,将gj;t和Gt分别记为

Fomin 和Zelevinsky[13]猜测g-向量可以用来参数化丛单项式且G-矩阵也有类似的符号一致性(参见[13,猜想6.13]).最近Gross 等[18]给出了这两个猜想的肯定回答.

定理7([18,定理0.3 和定理5.11])(1) 不同的丛单项式有不同的g-向量;(2) 对任意的t ∈Tn,矩阵Gt在整数上可逆且其行向量具有符号一致性.

注5Derksen 等[32]利用带势箭图的decorated 表示首先在B为斜对称的条件下证明了定理7.随后,Plamondon[33]和Nagao[5]分别用丛倾斜理论和Donaldson-Thomas 不变量理论在此条件下给出了新的证明.

c-向量与g-向量之间存在如下的tropical 对偶关系,该结果是[35]和定理6 的直接推论.

定理8设S是矩阵B的斜对称化子.对任意的t ∈Tn,有

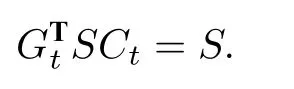
注6(1) 在B为斜对称矩阵的情形,Nakanishi[36]首次明确地证明了定理8 (同时参见[5,33,37]).随后Nakanishi 和Zelevinsky[35]在假设c-向量符号一致性的前提下证明了该定理.

(2)在c-向量符号一致性的前提下,文献[35]中定理8 的证明是初等的.另一方面,Nakanishi和Zelevinsky 发现丛代数中的诸多性质和猜想都可以通过定理8 及初等的方法证明.因此,尝试寻找c-向量符号一致性的初等证明也是非常有意义的.

4.3 F-多项式与f-向量

由定理1 知,对任意的t ∈Tn及j ∈[1,n],

根据[13]的命题5.6,下述命题与定理6 是等价的.

命题1对任意的j ∈[1,n]及t ∈Tn,多项式Fj;t(y)有唯一的次数最大的单项式,其系数为1且Fj;t(y)的其他系数非零的单项式都整除该单项式.

定义13对任意的j ∈[1,n]及t ∈Tn,记fj;t ∈Zn为多项式Fj;t(y)的次数最大的单项式的次数向量.称fj;t为丛代数A()在顶点t处的第j个f-向量,Ft=(f1;t,···,fn;t)为丛代数A()在顶点t处的F-矩阵.

例2显然,对任意的j ∈[1,n],=1.由此可知=0.

注7(1) 与c-向量和g-向量类似,f-向量也可以用递归的方式定义:

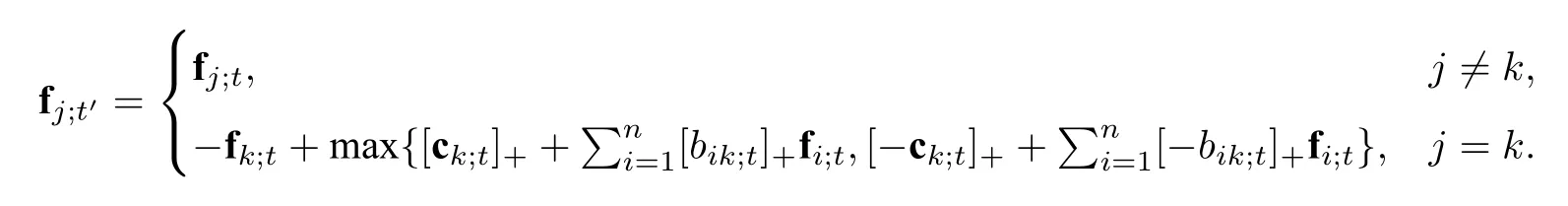
(2) 利用(1)可以将f-向量和F-矩阵推广至一般系数的丛代数.此时,为了强调它们与t0和矩阵B的关系,记fj;t和Ft分别为

5 一般系数的丛代数

在本节中,设P 为半域,(u,v,B)为系数属于P 的带标记的种子.固定(u,v,B)的一个丛模式使其以t0为根.记A(Σt0)为该丛模式的丛代数.特别地,对任意的t ∈Tn,有

为了符号的简便,记

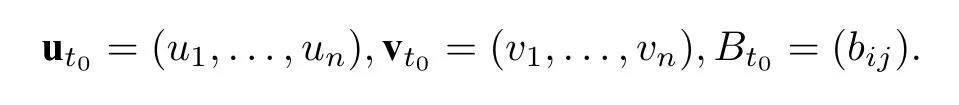
5.1 分离公式

5.2 c-向量与丛

根据注3 和注4,对丛代数A() 利用递归的方式定义c-向量和g-向量.至此,对任意的j ∈[1,n]及t ∈Tn,有c-向量cj;t,g-向量gj;t,矩阵Ct=(c1;t,...,cn;t)和Gt=(g1;t,...,gn;t).称Ct和Gt分别为丛代数A()在顶点t处的C-矩阵和G-矩阵.

显然,对于矩阵Ct和Gt,定理6 和8 仍然成立.另一方面,由[21]的命题3 知,定理7 对丛代数A()仍成立.

用C(t)表示矩阵Ct的列向量构成的集合,C+(t)表示C(t)中的所有正向量构成的子集.令

由定理6 及注3 易知,

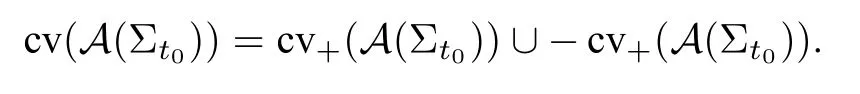
下述结论是定理7 和8 的直接推论.

推论1(1) 对任意的t,t′ ∈Tn,[ut]=[ut′]当且仅当C(t)=C(t′);(2) 丛代数A(Σt0)为有限型当且仅当|cv(A())|＜∞.

注8在文献[38]中,曹培根等利用丛变量的正性和c-向量的符号一致性对主系数丛代数证明了推论1(1).Seven[39]对主系数丛代数证明了推论1(2)(参见[34,定理A.5]).

推论1 表明C-矩阵也可以用来参数化丛.受代数表示论相关结果的启发,我们猜测每个顶点处的正c-向量集合就足以参数化丛.特别地,有如下猜想.

猜想3对任意的t,t′ ∈Tn,[ut]=[ut′]当且仅当C+(t)=C+(t′).

根据[21]的命题3,只需要对平凡系数的丛代数证明上述猜想.目前已知猜想3 对下述丛代数成立:

· 斜对称有限型丛代数;

· 秩为2 的丛代数;

· Markov 丛代数;

· 无环丛代数且初始种子无环.

最近,曹培根等[40]对Poisson 丛代数证明了上述猜想的一个类似版本.

5.3 f-向量与丛

根据注7,对丛代数A()利用递归的方式定义F-矩阵,因此,对任意的t ∈Tn,有矩阵Ft,称其为丛代数A()在顶点t处的F-矩阵.Gyoda 和Yurikusa[41]猜测F-矩阵也可以用来参数化丛.

猜想4([41,猜想4.4])对任意的t,t′ ∈Tn,ut=ut′当且仅当Ft=.

Gyoda 与Yurikusa[41]对曲面相关的丛代数验证了上述猜想.事实上,结合[42]与[28]知,上述猜想对斜对称有限型丛代数成立.类似地,由[42]与[30]知,上述猜想对斜对称仿射型丛代数也成立.最近,Gyoda[43]对所有的有限型丛代数与秩为2 的丛代数验证了上述猜想.

5.4 f-向量与相容性函数

付昌建与Gyoda[24]发现F-矩阵的(i,j)元只与相应的丛变量相关,而与具体的包含丛变量的丛的位置无关.

命题3 ([24,定理3.3 (2)])设x,x′为两个丛变量,i,j ∈[1,n] 及t,t′ ∈Tn使得x=ui;t,x′=uj;t′,则矩阵的(i,j)元与i,j,t,t′的选取无关.

命题3 保证了下述相容性函数(compatibility degree)是良定的.

定义14对任意的x,x′ ∈X,若x=ui;t,x′=uj;t′,则定义

称映射(-‖-):X ×X →Z 为丛代数A(Σt0)的相容性函数.

上述定义推广了Fomin 和Zelevinsky[3]关于有限根系的经典相容性函数(参见文献[45]).特别地,当丛代数A()为有限型丛代数时,定义14 中的函数与[3]中的函数一致.

将种子(u,v,-BT)赋予顶点t0得到一个丛模式.设x=ui;t为丛代数A()在顶点t处的第i个丛变量,记x∨为丛代数A()在顶点t处的第i个丛变量.显然,若B为斜对称的,则x=x∨.文献[24]证明了相容性函数有如下性质.

命题4([24,命题4.14])设x,x′为丛代数A()的任意两个丛变量,S=diag{s1,...,sn}为可斜对称化子,则有

(1) (x‖x′)=((x′)∨‖x∨).特别地,若B为斜对称的,则(x‖x′)=(x′ ‖x);

(2) 若x=ui;t,x′=uj;t′,则si(x‖x′)=sj(x′ ‖x).特别地,(x‖x′)=0 当且仅当(x′ ‖x)=0;

(3) (x‖x′)=0 当且仅当存在顶点s ∈Tn使得x,x′ ∈[us].

文献[24]进一步猜测相容性函数可以刻画交换对.特别地,有

猜想5([24,猜想4.23])设x,x′为丛代数A()的两个丛变量,则(x,x′)为一个交换对当且仅当(x‖x′)=(x′ ‖x)=1.

在[24]中,付昌建与Gyoda 利用加法范畴化对某些重要的丛代数类证明了上述可交换猜想.最近,曹培根、Keller 和覃帆对一般情形验证了可交换猜想成立.

注9文献[21]利用d-向量定义了丛代数A()的d-相容性函数.该函数也可以看作经典相容性函数的推广.但是d-相容性函数不满足经典相容性函数的部分性质,如定理4(1).另一方面,d-相容性函数也不满足交换猜想(参见[24,第6.5 节]).