A variational principle for Bowen estimation entropy of nonautonomous dynamical systems
2022-03-31LiuLeiPengDongmei
Liu Lei,Peng Dongmei
(School of Mathematics and Statistics,Shangqiu Normal University,Shangqiu 476000,China)
Abstract:In this paper,we study the Bowen estimation entropy for nonautonomous dynamical systems,which is an extension of the classical definition of Bowen entropy in autonomous dynamical systems.We show that the Bowen estimation entropy can be determined by the local estimation entropies of measures for nonautonomous dynamical systems.Also,we establish a variational principle for Bowen estimation entropy on compact subsets in the context of nonautonomous dynamical systems.
Keywords: Bowen estimation entropy,measure-theoretic lower α-estimation entropy,nonautonomous dynamical system,variational principle
1 Introduction
In 1958,Kolmogorov applied the notion of entropy from information theory to ergodic theory.Since then,the concepts of entropy,in particular the topological entropy and measure theoretic entropy,were useful for studying topological and measuretheoretic structures of dynamical systems,that is,topological entropy[1-4]and measuretheoretic entropy[4-6].For instance,two conjugate systems have the same entropy and thus entropy is a numerical invariant of the class of conjugated dynamical systems.The theory of expansive dynamical systems has been closely related to the theory of topological entropy[7-9].Entropy and chaos are closely related,for example,a continuous map of interval is chaotic if and only if it has a positive topological entropy[10].
Reference[11]introduced the topological entropy for any set in a topological dynamical system by a way resembling Hausdorff dimension.Bowen′s topological entropy plays a key role in topological dynamics and dimension theory[12].Reference[13]defined the measure-theoretic entropy for Borel probability measures from the idea of Reference[14]and showed that there is certain variational principle between Bowen topological entropy and measure theoretic entropy for arbitrary non-invariant compact set of a topological dynamical system.References[15-17]characterized the smallest bit rate for an exponential state estimation with a given exponentαfor a continuous-time system on a compact subsetKof its state space.As a measure for this smallest rate they introduced a quantity named estimation entropyhest(α,K),which coincides with the topological entropy onKwhenα=0,but forα>0 is no longer a purely topological quantity.Reference[18]studied the notion of estimation entropy and gave this quantity that measures the smallest rate of information about the state of a system above which an exponential state estimation with a given exponent is possible.Reference[19]discussed the estimation entropy of free semigroup action.Reference[20]studied Bowen estimation entropy and gave a variational principle for Bowen estimation entropy.
In contrast with the autonomous discrete dynamical systems and the continuoustime systems,the properties of the estimation entropies for the nonautonomous dynamical systems have not been fully investigated.A nonautonomous discrete dynamical systems is a natural generalization of a classical dynamical systems,its dynamics is determined by a sequence of continuous self-maps on a compact metric space.The topological entropy of nonautonomous discrete dynamical systems was introduced by Reference[21]and the topological and measurable theory of these systems were developed among others in References[22-30].
Reference[31]defined the Bowen topological entropy of nonautonomous dynamical systems.Their results give quite a number of contributions dealing with Bowen topological entropy of nonautonomous dynamical systems.Based on their works,we give a definition of estimation entropy of nonautonomous dynamical systems which allow us to study it by using the Carathéodory dimension structure.The Hausdorff dimension can be determined with the help of Billingsley′s theorem[32].For the Bowen topolog-ical entropy,Reference[33]gave an analogue of the Billingsley′s theorem.Motivated by Reference[33],we show that the Bowen estimation entropy can be determined via the local estimation entropies of measures for nonautonomous dynamical systems and this result can be considered as an analogue of Billingsley′s theorem for the Hausdorff dimension.By our definitions of estimation entropy and lower local estimation entropy,we obtain the following results.
We extend the result of Reference[33]to nonautonomous dynamical systems and establish an analogue of the Billingsley′s theorem between lower local estimation entropy and the Bowen estimation entropy(Theorem 3.1).
We establish a variational principle for estimation entropy on compact subsets in the context of nonautonomous dynamical systems(Theorem 4.1).
2 Preliminaries
Let N and N+denote the sets of all non-negative integers and all positive integers respectively.We call(X,φ)is a nonautonomous dynamical system(NADS for short),if(X,d)is a compact metric space andφ:[0,+∞)×X→Xis a continuous map withφ(0,x)=xfor everyx∈X.Given a NADS(X,φ).For allt∈[0,+∞)andα≥0,we define


Remark 2.1From(2.1)and(2.2),we have
2.1 α-estimation entropy for NADS
Givenϵ>0,α≥0 andt∈[0,+∞).A subsetF⊆Xis an(t,ϵ,α)-spanning set ofXwith respect toφif for anyx∈X,there existsy∈Fsuch that.A subsetE⊆Xis an(t,ϵ,α)-separated set ofXwith respect toφif for anyxyinE,one has
We note that since the spaceXis compact,it follows that(t,ϵ,α)-spanning set and(t,ϵ,α)-separated set are finite.Letsest(t,ϵ,α,X,φ)be the minimal cardinality of any(t,ϵ,α)-spanning set ofXand the quantityrest(t,ϵ,α,X,φ)be the maximal cardinality of(t,ϵ,α)-separated set ofX.We sometimes writesest(t,ϵ,α,X,φ,d)andrest(t,ϵ,α,X,φ,d)when we need to emphasise the metricd.
Remark 2.2(1)Ifϵ1<ϵ2,thensest(t,ϵ1,α,X,φ)≥sest(t,ϵ2,α,X,φ).
(2)Ifϵ1<ϵ2,thenrest(t,ϵ1,α,X,φ)≥rest(t,ϵ2,α,X,φ).
(3)We havesest(t,ϵ,α,X,φ)≤rest(t,ϵ,α,X,φ)≤sest(t,ϵ/2,α,X,φ)for everyϵ>0.
Definition 2.1Givenϵ>0 andα≥0.Set

Definition 2.2Let(X,d)be a compact metric space and(X,φ)a NADS.Theα-estimation entropy ofφrelative todis defined to be

Remark 2.3IfK⊆Xis a compact set,we call

α-estimation entropy ofK.
By Reference[18],we give the following example that showshest(α,X,φ)depends on the metricdofX.
Example 2.1[18]Letφ(s,x)=e-sxonX=[0,1]andα=2.Consider the metrics

Since the system is linear,the inequalityd(φ(s,x),φ(s,y)) LetM(X)denote the set of all Borel probability measures onX.We give the following new definition from the idea of Reference[14]. Definition 2.3Let(X,φ)be a NADSµ∈M(X),α≥0 andx∈X.Then we call the measure-theoretic lower localα-estimation entropy ofµat the pointx∈X. Definition 2.4Let(X,φ)be a NADS,µ∈M(X),α≥0 andx∈X.The measure-theoretic lowerα-estimation entropy ofµis defined by Given a NADS(X,φ).We denoteφi(x):=φ(i,x)fori∈N andx∈X.Let.For anyn∈N+,α≥0 andx,y∈X,we define For alln∈N,ϵ>0,α≥0 andx∈X,set Definition 2.5Letµ∈M(X)andα≥0.The measure-theoretic lowerαestimation entropy ofµis defined by In this section,we give the definition and some basic properties of Bowenαestimation entropy for NADSs.

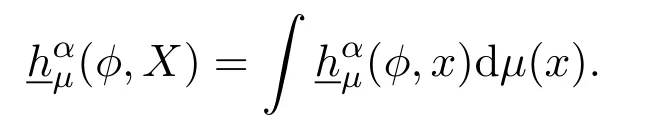



2.2 Bowen α-estimation entropy for NADS



2.3 Weighted Bowen α-estimation entropy for NADS

3 Billingsley type theorem of Bowen α-estimation entropy for NADS





4 Variational principle of Bowen α-estimation entropy for NADS
4.1 Equivalenceand




4.2 Variational principle for Bowen α-estimation entropy



