冯丽娜 方小利

(绍兴文理学院 数理信息学院，浙江 绍兴 312000)

0 引言

Turaev在研究中引入了Turaev辫子群范畴[1]，这类范畴可以产生3维同伦量子场论.Kirillov发现，这类范畴还提供了合适的数学工具来描述共形场论研究中出现的Orbifold模型[2].同时，Virelizier通过Turaev辫子群范畴构造了Hennings型不变量[3].因此Turaev辫子群范畴研究引起了代数专家强烈的兴趣.最近，一些构造Turaev辫子群范畴的新结果也陆续发表出来，为了构造新的非平凡结合子的Turaev辫子群范畴，Fang等介绍了拟三角拟Turaev群余代数，同时证明了拟三角拟Turaev群余代数的表示也是此类Turaev辫子群范畴[4]，拟三角Turaev群余代数的进一步研究还有不少[5-6].Virelizier[7]给出了Hopf群余代数中对极的定义以及若干性质，这些性质在Hopf群余代数的研究中起到了重要作用.拟Hopf群余代数的对极在拟三角拟Turaev群余代数的研究中占有重要地位，不同于一般Hopf群余代数情形，拟Hopf群余代数的对极有着很多不同的性质，但在参考文献[4-6]中，并没有对对极的相关性质进行深入研究.本文主要讨论拟Hopf群余代数上关于对极的若干性质，证明拟Hopf群余代数的对极在一般意义下不唯一.

在本文中，k为一个固定域，所有代数，线性空间等都在域k上，未经说明的⊗表示⊗k.对于乘法，使用Sweedler-Heyneman记法[8-9].

1 拟Hopf群余代数

首先规定：一族带有余乘法和余单位的代数({Hα},△,ε))是指它是一族结合且带有单位k-代数H={Hα}α∈π和带有一族代数映射

△={△α,β:Hαβ→Hα⊗Hβ}α,β∈π(余乘法)和ε:H1→k(余单位).

定义 1:设H=({Hα},△,ε)是一族带有余乘法和余单位的代数.若存在可逆元素(结合子)的Φ={Φα,β,γ∈Hα⊗Hβ⊗Hγ}α,β,γ∈π满足：

(idα⊗△β,γ)△α,βγ(h)Φα,β,γ=Φα,β,γ(△α,β⊗idγ)△αβ,γ(h)(h∈Hαβγ),

(1)

(idα⊗ε)(△α,1(h))=h,(ε⊗idα)(△1,α(h))=h(h∈Hα),

(2)

(1α⊗Φβ,γ,θ)(idα⊗△β,γ⊗idθ)(Φα,βγ,θ)(Φα,β,γ⊗1θ)

=(idα⊗idβ⊗△γ,θ)(Φα,β,γθ)(△α,β⊗idγ⊗idθ)(Φαβ,γ,θ),

(3)

(idα⊗ε⊗idβ)(Φα,1,β)=1α⊗1β,

(4)

则称H=({Hα},△,ε)为拟半群余代数.

注1.1：用Sweedler-Heyneman记法，则△α,β(h)=h(1,α)⊗h(2,β)，其中记号∑省略.采用以上记法对于所有的h∈Hαβγ,我们记：

(△α,β⊗idγ)△αβ,γ(h)=h(1,αβ)(1,α)⊗h(1,αβ)(2,β)⊗h(2,γ)

证明：注1.1的证明见参考文献[4].

我们分别用大写字母表示结合子Φ, 用小写字母表示结合子的逆Φ-1，即：

用Sweedler-Heyneman记法, 式(1)至式(4)可以记为：

(5)

h(1,α)ε(h(2,1))=h=ε(h(1,1))h(2,α),h∈Hα,

(6)

(7)

(8)

两个拟半群余代数({Aα},△A,εA,ΦA)和({Bα},△B,εB,ΦB)之间的同态是k-线性映射族f={fα:Aα→Bα}α∈π满足：

(9)

(10)

且对于所有的α∈π，fα是一个代数态射.进一步，对于所有的α∈π，若fα是双射，那么称它为拟半群余代数同构.

注1.2：(1)若拟半群余代数H中的Φ是平凡的，那么Φα,β,γ=1α⊗1β⊗1γ,H是一个半群余代数[1,7].

(2)若π是平凡的，一个拟半群余代数是一个拟双代数[11].

命题1：设H={Hα}α∈π是一个拟半群余代数，那么

(ε⊗idα⊗idβ)(Φ1,α,β)=1α⊗1β=(idα⊗idβ⊗ε)(Φα,β,1),

(11)

(12)

定义2：一个拟Hopf群余代数是一个拟半群余代数H=({Hα},△,ε)带有一族可逆反自代数同态(对极)S={Sα:Hα→Hα-1}和元素τ=(τα)α∈π以及υ=(υα)α∈π，对于所有的α∈π,τα,υα∈Hα满足[4]：

Sα(a(1,α))τα-1a(2,α-1)=ε(a)τα-1,

(13)

a(1,α)υαSα-1(a(2,α-1))=ε(a)υα,

(14)

(15)

(16)

根据定义，自然可得以下这两个命题，命题3的证明可见参考文献[7].

命题2：ε(S1(a))=a,ε(τ1)ε(υ1)=1，

命题3：设H={Hα}α∈π是一个拟Hopf群余代数，那么{α∈π|Hα≠0}是π的一个子群.

接下来构造一些拟Hopf群余代数的例子.

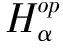
(III)反和余反拟Hopf群余代数(Hop,cop)：设H={Hα}α∈π是一个拟Hopf群余代数，可以通过H定义一个H的反和余反拟Hopf群余代数.

2 对极的若干性质

为研究对极与余乘法和结合子相容性，需要定义两族元素χ={χα,β∈Hα⊗Hβ}α,β∈π和δ={δα,β∈Hα⊗Hβ}α,β∈π其中：

(17)

(18)

引理1：(1)对于所有的α,β∈π,

(19)

(20)

(2)对于所有的a∈H1,

(21)

(22)

(3)对于所有的α,β∈π,

(23)

(24)

证明：(1)对于所有的α,β∈π, 有

据式(3)

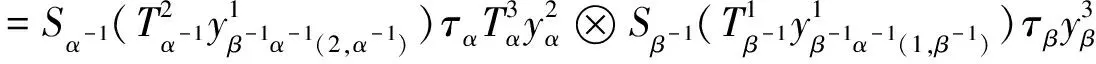
据式(4),(13)

同样的方法可得公式δα,β.

(2)根据式(17)中χαβ的定义，得到

据式(17)

据式(1)

据式(13)

=ε(a)χα,β

类似可证式(22).

(3)对于所有的α,β∈π,计算可得

据式(17),(18)

据式(3)

据式(13),(14)

据式(3)

据式(4),(11)，(13)，(14)

据式(3)

据式(4),(11),(13),(14)

据式(15)

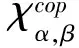
gβ-1,α-1(a(1,β-1α-1))ρα,βfα,β(a(2,αβ))=ε(a)ραβ,

(25)

(26)

(27)

(28)

证明：证明类似于本文定理1的证明.

通过元素χ和δ, 定义一族元素

(29)

F与对极有密切的关系，可见以下命题.

命题4：F是一个可逆元素，带有逆元

(30)

而且有

χα,β=Fα,β△α,β(ταβ),

(31)

(32)

对极与余乘法通过下式相容：

(33)

而且对极与结合子通过下式相容：

(34)

证明：为应用引理2设

根据引理1，这些条件都是满足的，因此得到一族可逆元素F,F和F-1刚好分别就是式(29)和式(30)所给出的，且等式(31)—式(33)成立.还需证明等式(34)，根据式(29)和式(33)，可得

(35)

(36)

我们将式(34)的证明简化为下列等式的证明.

=(1α⊗Fβ,γ)(idα⊗△β,γ)(χα,βγ)Φα,β,γ

(37)

根据式(17)、式(31)和式(33),可得

据式(3)

据式(1)

=(1α⊗Fβ,γ)(idα⊗△β,γ)(χα,βγ)Φα,β,γ

因此，完成了证明.

3 拟Hopf群余代数对极的唯一性

不同于一般Hopf群余代数情形，拟Hopf群余代数的对极在一般意义下不唯一，可以借助一系列可逆元素(κα)α∈π和κα∈Hα通过原来的Sα,τα,υα如下方式定义

(38)

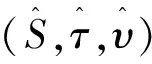
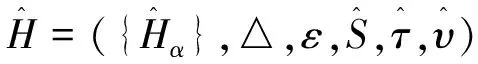
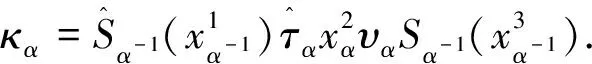
据式(13)

据式(1)

据式(14)

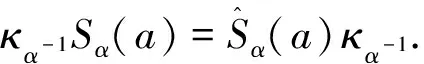
据式(11),(13)

据式(11),(13)

据式(3)

据式(12),(13)

据式(15)

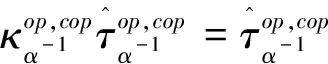
通过Sκ定义的χκ,δκ和Fκ与原S定义的χ,δ,F的关系如下：

证明：其中χκ和δκ可以直接根据χ和δ的定义得到.对于Fκ，由于