廖彬彬,徐建桥，陈晓东*,孙和平,周江存

1 中国科学院精密测量科学与技术创新研究院 大地测量与地球动力学国家重点实验室，武汉 430077 2 中国科学院大学，北京 100049

0 引言

月球是离地球最近的天体，是人类迈向太空的第一站.研究月球内部结构对人类进行空间探索、了解地月系统的演化、开采并利用月球资源等方面具有重要意义(Smith et al.,2017;Zhao et al.,2018；Sun et al.,2019).20世纪阿波罗计划在月球表面开展了一系列月震观测实验，这些月震观测数据使人类对月球内部结构有了初步的认识.早期月震的分析结果表明月球内部主要存在以下几个构造圈层：一个厚度约为50～70 km的月壳、一个厚度较大的月幔且在月幔深处存在一个低速层(Nakamura et al.,1974;Goins et al.,1981).后来月球极移和月球磁场的观测结果证明了月球存在一个液态的外核(Williams et al.,2001；Shimizu et al.,2013).在阿波罗计划之后，高分辨率遥感卫星技术的应用以及近年来对早期月震数据的重新处理使得对月球结构的认识有了新的突破(Hao et al.,2018).Sugano 和 Heki(2004)利用LP(Lunar Prospector，月球勘探者)卫星的重力观测数据推断月壳厚度约为20～60 km.Khan等(2000)利用非线性贝叶斯方法对阿波罗月震数据进行了重新处理，结果表明在月壳内深度为20 km以及45±5 km处存在速度间断面，并且月幔内深度为500 km处P波速度与S波速度显著增加.Lognonné等(2003)利用体波走时数据通过随机搜索方法发现月幔内深度500 km以及750 km处均存在速度间断面.对于月球更深部分的分层结构，Konopliv等(1998)基于LP卫星得到的月球质量、平均转动惯量以及重力数据推测：如果月核完全由固态铁组成，则半径为220 km到370 km之间；而如果月核为液态的Fe-FeS共晶体，则半径为330～590 km之间.Garcia等(2011)基于大地测量观测数据(包括月球质量、转动惯量以及勒夫数)以及月震数据得到了月球结构模型VPREMOON，其中的月核半径为380±40 km，月核平均密度为5200±1000 kg·m-3.Yan等(2015)通过Monte Carlo方法得到月核半径为370 km.而Weber等(2011)通过反演得到月核由固态内核以及液态外核组成，其中固态内核半径为240 km，液态外核半径范围为240～330 km．Williams等 (2014)以Weber等(2011)月球内部结构模型为初始模型，利用GRAIL(Gravity Recovery and Interior Laboratory,重力重建与内部结构实验室)重力场数据计算了月球2阶固体潮勒夫数、平均密度以及平均转动惯量等物理量，通过调整低速区弹性参数、低速区厚度以及内外核厚度，得到了满足GRAIL观测数据的5个月球内部结构模型 (GPM 1—5).然而Matsuyama等(2016)认为Williams等(2014)采用的勒夫数k2=0.02422±0.000012是粘弹性月球的引潮位响应，经过改正后给出了弹性月球的勒夫数为k2=0.0220±0.0017.并且Matsuyama等(2016)利用Markov Chain-Monte Carlo方法进行反演，结果显示月幔底部低速区存在的概率约为50%.综上所述，从上面目前国内外对月球结构研究结果可以看出，现阶段对月球结构模型的认识，特别是月球深部结构的认识，仍然存在许多的不确定性，这也是至今没有一个月球内部结构模型被广泛认可和采用的根本原因.

目前可以用来反演月球内部结构的数学方法有很多，各种方法或多或少都存在一定的局限性.传统线性反演方法要求模型参数与观测数据之间的映射是(拟)线性的，然而实际中观测数据与模型的关系往往是非线性的，甚至可能都不是一一对应的映射关系(Tarantola,2005).已有的研究结果表明利用非线性Bayes反演方法可以很好解决传统线性反演方法的不足(De Wit et al.,2013).Bayes反演方法基于Bayes理论，利用观测数据d、模型的先验分布σ(m)和似然函数L(d|m)计算模型参数后验概率密度分布σ(m|d)，从而获得模型的最优解，即最大后验概率对应的模型(De Wit et al.,2013).由于采用了更加复杂的概率模型与参数估计方法，Bayes反演方法完全摆脱最小二乘方法要求观测数据和模型参数之间存在线性关系的限制.Bayes反演方法通常利用Monte Carlo方法来实现(Käufl et al.,2013)，然而Monte Carlo方法受限于“维度诅咒”(Bellman,1961)，往往计算量巨大，需要较长的计算时间.另一种可行的Bayes反演方法是混合密度神经网络方法(Mixture Density Neural Network，MDN)，其基本原理是建立一个以观测数据为输入，以模型参数的后验概率密度分布为输出的神经网络(Bishop,1995).与Monte Carlo方法相比，MDN方法可以避免“维度诅咒”，从而极大地提高计算效率(De Wit et al.，2013).此外MDN方法还可以得到观测数据与模型参数之间的函数关系，为进一步分析月球内部结构模型的精度提供了可能.

本研究采用Williams等(2014)基于GRAIL观测任务给出的平均密度ρ和平均转动惯量MOI以及Matsuyama等(2016)给出的弹性勒夫数k2作为观测约束，通过MDN方法获得了月球内部结构模型的低速层、外内核的半径、P波和S波速度等8个模型参数的后验概率密度分布，计算了平均月球内部结构模型Mean、最大后验概率密度对应的MAP模型以及满足1-σ准则的月球内部结构模型的参数范围.最后利用观测值与月球内部结构模型的参数之间的函数关系，采用不同观测值观测误差范围内月球内部结构模型参数的变化幅度作为度量，定量地分析了不同观测值的精度对月球内部结构模型的影响.

1 数据和方法

对月球内部结构的反演工作主要由两部分组成：(1)以Weber等(2011)的月球内部结构模型为初始模型，对内外核及低速区的厚度、P波及S波速度进行均匀采样，得到所有可能的月球内部结构模型，然后正演计算得到对应的固体潮勒夫数、平均密度及平均转动惯量；(2)利用混合密度神经网络方法和上面计算的三个观测值，得到对应月球内部结构模型的后验概率密度.

1.1 观测数据的正演计算

假设月球是一个非自转、完全弹性、各向同性以及横向均匀的分层球体，并且各个圈层的密度以及弹性参数均为常数.Matsumoto等(2015)利用Bayes方法反演了月球内部结构，他们的结果表明：月幔底部低速区以及月核的半径、弹性参数和密度都存在很大的不确定性，而低速区以上的部分模型参数的不确定性相对较小.因此本研究假设在低速区以上部分月球内部结构模型参数为定值，均采用Weber等(2011)给出月球内部结构模型中的数值，而低速区以下的模型参数则为反演的自由度.此外由于观测值个数较少，出于简化反演问题的考虑，低速区与内外核的密度同样也采用Weber等(2011)给出月球内部结构模型中的对应数值.并且为了与嫦娥1号、Clementine等其他月球任务给出的月球半径观测数据吻合(Ping et al.,2009;Zuber et al.,2013;Smith et al.,2017)，Williams等(2014)建议将Weber等(2011)的月球内部结构模型中的半径调整为R=1737.151 km.最终在反演问题中需要考虑的模型参数总共8个，包括内核半径ri、内核P波速度VPi、内核S波速度VSi、外核半径ro、外核P波速度VPo、低速区半径rl、低速区P波速度VPl以及低速区S波速度VSl，所有参数先验的变化范围如表2中“先验模型范围”一列所示.假设8个模型参数的先验概率分布满足均匀分布，在表2给出的先验模型范围内对它们进行随机采样，总共生成100000个月球内部结构模型样本.

研究中观测值固体潮勒夫数k2、平均密度ρ以及平均转动惯量MOI的具体数值以及误差范围如表1所示.本文中固体潮勒夫数k2采用的是Matsuyama等(2016)给出的弹性勒夫数k2=0.0220±0.0017.为了获得上述100000个月球内部结构模型样本的模拟观测值，首先通过正演数值计算方法获得每个月球内部结构模型对应固体潮勒夫数、平均密度以及平均转动惯量的模拟观测值.其中在求解二阶潮汐勒夫数时，需要求解一个由动量平衡方程与泊松方程组成的二阶偏微分方程组边值问题，本研究采用廖彬彬等(2019)给出的谱元法进行数值计算.对于平均密度和平均转动惯量，则用Gauss-Legendre数值积分方法进行计算(Quarteroni，2009).此外由于实际观测值存在误差，因此需要对上面正演计算得到的模拟观测值加上观测误差才能得到实际观测值.研究中假设三个观测值在误差范围内服从均匀分布，对其进行随机采样得到相应的观测误差，然后加上对应的观测值便可得到之后训练神经网络所需要的模拟观测值.

表1 反演计算采用的观测值及其精度Table 1 Observations and their accuracies used in the inversion calculation

1.2 用混合密度神经网络方法反演后验概率密度

神经网络反演方法主要特点在于它可以解决反演过程中的“非线性”和“不唯一性”等问题.该方法与一般采样反演方法相比，计算效率更高，关键是还可得到模型参数后验概率密度分布与观测值间的映射关系.这种映射关系可用来进一步研究观测值精度对模型精度的影响，也是本文研究模拟观测值精度对月球内部结构模型精度影响采用的主要数学方法.神经网络的数学本质是实现从输入层(Input layer)到输出层(Output layer)之间任意映射关系的近似表达，其映射关系如图1所示，可用下面公式(1)和(2)来描述(De Wit et al.,2013)：

图1 神经网络映射关系示意图Fig.1 Schematic diagram of the neural network mapping relationship

(1)

(2)

混合密度神经网络是以观测数据为输入层，以其反演的结构模型后验概率密度函数为输出层的两层神经网络(Bishop,2006).MDN方法输出层的后验概率密度函数为高斯混合分布，其定义如下：

(3)

式中w表示公式(1)和(2)中的权重和偏置，αi是Softmax函数，它代表第i个高斯核函数φi的权重.高斯核函数φi定义为

φi(m|d;w)=

(4)

式中c为模型参数m的维度，μi和σi分别为第i个高斯核函数的均值及标准差，μi、σi和αi可以分别控制第i个高斯核函数的中心位置、宽窄、高低(权重).不同于传统线性反演方法中以单个高斯分布模型作为概率模型，本研究月球内部结构模型参数所用的概率模型(见公式(3))是M个高斯分布的线性组合.理论上随着高斯核函数个数M趋近于无穷大，公式(3)给出的概率模型可以近似地表示任意概率分布函数(Bishops,1995).利用公式(3)给出的概率模型，可实现从一个观测值到多个可能模型值(平均值μi)之间的映射关系，从而解决了反演的“不唯一性”问题.此外通过混合密度神经网络方法，还实现了由观测数据到概率模型参数μi、σi和αi的函数映射，而不仅限于线性映射，因此该方法解决了传统最小二乘方法只能处理观测值与模型参数为线性映射的问题，这也是本研究选用该方法的主要原因.

在使用MDN反演方法的过程中，构建了一个以固体潮勒夫数、平均密度及平均转动惯量的观测值为输入层，以低速层半径、内外核的厚度、P波和S波速度的联合后验概率分布(即公式(3))的参数μi、σi和αi为输出层的两层神经网络.该神经网络输入层节点个数为I=3，其激活函数为“Rule”函数；隐藏层节点个数为50，其激活函数为g(a)=a；而对于输出层，设高斯核个数M为10，节点个数为K=170.各项超参数(训练步数、批训练大小、优化器类型、激发函数类型以及节点个数等)的具体选择方法将在下面进行叙述.

神经网络的训练过程是一个不断更新节点权值和每一层的偏置(即公式(1)和(2)中的w与b)，从而使得损失函数接近最小的过程.MDN方法的损失函数loss是后验分布函数(公式(3))的似然函数(Bishop，1995)，它可以用来衡量所输出的概率模型与训练数据之间的相似程度，其定义如下：

(5)

其中N为训练样本总数.训练所采用的最优化方法是随机梯度下降法，通过这种方法可将训练集数据分批逐次地代入损失函数当中，而不必一次性计算所有训练集数据损失函数的和(Goodfellow et al.,2016).本研究采用的随机梯度下降算法是“Adam”算法.为了避免最优化解陷入局部最优解，需要对神经网络进行多次训练，从中选择损失函数最小的解，并且在每次训练之前需要对权值进行不同的初始化(Bishop,1995).此外，为了避免输出的月球内部结构模型中各层半径出现负值，本文采用log(ri)、log(ro-ri)和log(rl-ro)代替内核半径ri、外核半径ro以及低速区半径rl作为神经网络的输出.最后通过z-socre标准化方法对观测值与模型参数进行预处理可以有效避免训练过程中出现“梯度饱和”(De Wit et al.,2013).

在神经网络训练完后，还要对其泛化能力进行评估，神经网络的泛化能力是指其能正确预测未参与训练数据的能力.为了度量神经网络的泛化能力，本研究以8∶1∶1的比例将100000组观测数据与对应模型参数成对组成的数据集分成训练集、测试集以及验证集，三者中只有训练集参与神经网络的训练，后面两者作为检验标准分别在训练过程中超参数的选择阶段和训练结束后结果评价阶段对神经网络的泛化能力进行评估(Goodfellow et al.,2016).与传统最优化问题不同，为了提高训练得到神经网络的泛化能力，避免“过拟合”的发生，神经网络最优化的目标函数并非参与训练的训练集损失函数，而是未参与训练的验证集与测试集损失函数，训练集的损失函数仅仅为最优化过程提供了方向(Goodfellow et al.,2016).在训练过程中，利用验证集损失函数的大小来对训练过程中的各种超参数进行抉择.以训练步数的选择为例，图2中展示了1000个步长学习过程中训练集与验证集损失函数随训练步数的变化曲线.在上文给出的各种超参数的条件下，经过1000个步长时训练集和验证集的损失函数均趋近于收敛，且无明显过拟合现象.而经过1000个步长后，验证集的损失函数不再继续减小，因此我们将训练步长选为1000是合理的.在训练结束阶段，用测试集损失函数的大小对训练好的神经网络的泛化能力进行评估，最终得到的神经网络训练集的平均损失函数值为-1.88，验证集的平均损失函数值为-1.84，测试集的平均损失函数值为-1.82，三个值相差很小，说明未参与训练数据的损失函数与参与训练数据的损失函数相当，足以证明训练得到的神经网络模型具有足够强的泛化能力.

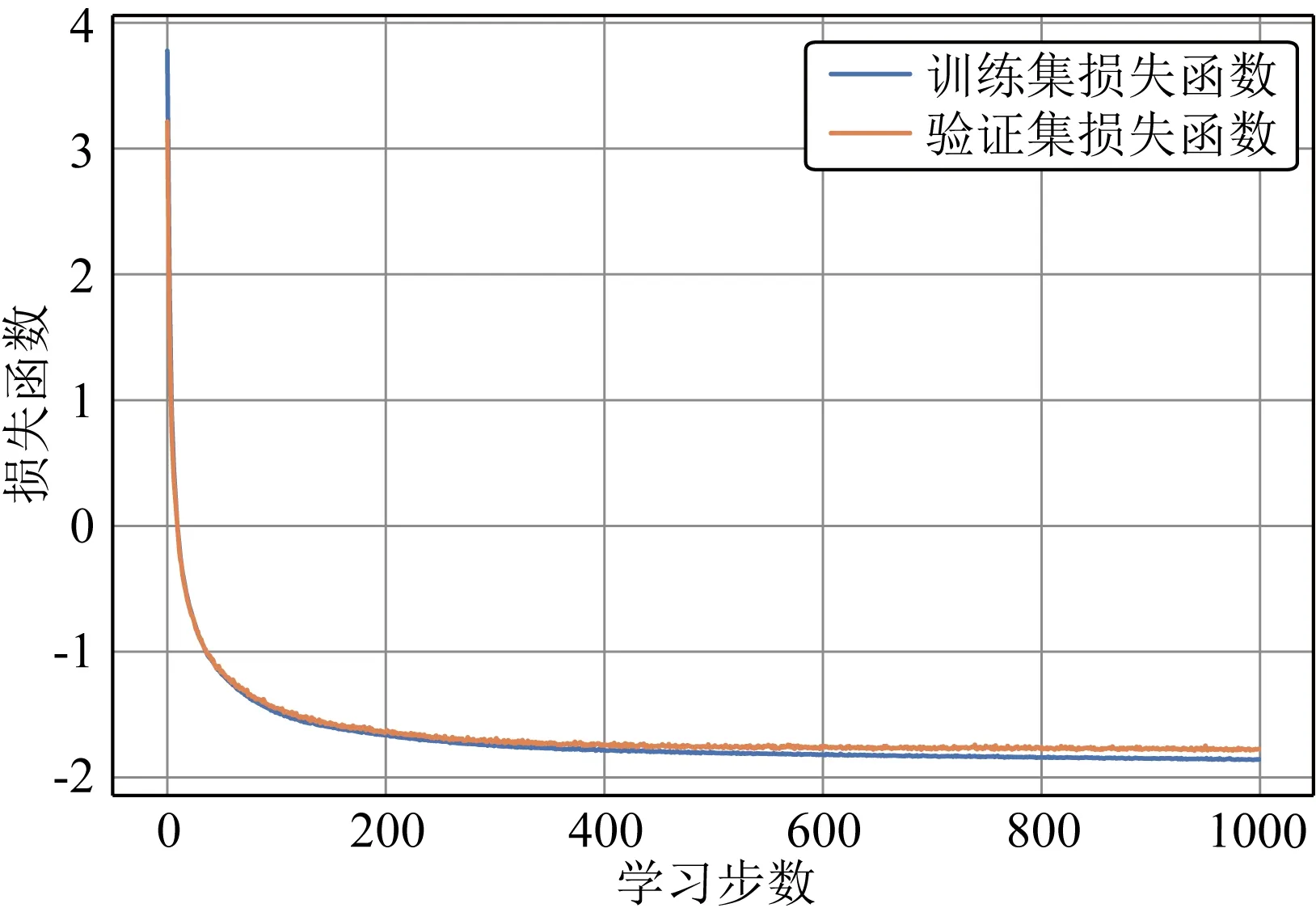
图2 学习曲线(训练集与验证集损失函数随训练步数的变化曲线)Fig.2 Learning curves (loss function′s variation curves of training set and verification set with the number of training steps)

2 计算结果与分析

为了验证混合密度神经网络(MDN)方法的有效性，需要将MDN方法的结果其与其他独立方法的结果进行比较，本研究将其与随机采样方法的结果进行比较.并且根据MDN方法得到模型参数后验概率密度分布对月球内部结构模型进行采样，并正演计算月球内部结构模型参数样本对应的模拟观测值，从而分析了MDN方法的结果与实际观测值误差的符合程度．然后基于模型参数的后验概率密度分布，计算平均月球内部结构模型(Mean模型)、最大后验概率密度对应的模型(MAP模型)以及基于1-σ准则给出的月球内部结构模型(1-σ模型).最后依据得到的不同观测值与模型参数间的函数关系，并利用模型参数在不同观测值误差范围内的变化幅度为度量，研究了不同观测值的观测精度对月球内部结构模型的影响.

2.1 MDN方法计算结果有效性的独立验证

由于似然函数不是一个绝对的评价指标，其对应的损失函数值为-1.82，并不能说明MDN方法的反演结果能有效地反映观测数据中所包含月球内部结构的全部信息.因此为了验证MDN方法结果的有效性，需要将MDN方法计算的结果与其他独立方法的结果进行比较.本研究用来对比的独立方法是随机采样方法，其主要步骤如下：(1)利用随机采样方法获得100000个月球结构模型样本，它们参数的变化范围如表2所示；(2)利用1.1节所述正演方法计算每个样本对应的观测值；(3)假设这些观测值在各自误差范围内满足均匀分布，对于步骤(2)中观测值落在误差范围内的样本加以保留，对于落入误差范围外的样本则拒绝，从而获得符合观测误差的月球结构模型样本.所采用的观测值及其误差范围如表1所示.

图3给出了MDN方法计算结果与随机采样方法获得的月球内部结构模型样本的比较.图3中蓝色为MDN方法的结果，其右侧和上侧是单个月球内部结构模型参数的边缘概率密度分布.由于随机采样方法受限于“维度诅咒”，最终100000个样本中符合观测误差的样本只有36个，在图中用红色“×”表示，并且这36个样本大部分都落在MDN方法联合概率密度分布的高密度区域，因此MDN方法的计算结果能够有效地表达随机采样方法结果的主要特征.以内核半径与外核半径联合概率密度分布为例，MDN方法得到二者的皮尔逊相关系数(Pearsonr)为-0.95，p值(显著性水平)为0，随机采样方法得到二者皮尔逊相关系数为-0.91，p值为5.4×10-24；由于二者的皮尔逊相关系数均接近-1，说明二者存在线性负相关关系，而p值均远小于0.05说明这种线性相关是显著的.MDN方法与随机采样方法的比较结果可证明MDN方法能有效解决月球内结构模型的反演问题，得到的解是非平凡解.

图3 MDN方法结果与随机采样方法结果的比较蓝色为MDN方法的结果，红色叉号为随机采样方法的结果．(a)内核半径与外核半径联合概率分布；(b)外核半径与低速区半径联合概率分布；(c)低速区P波与S波速度联合概率密度分布．Fig.3 Comparison of results obtained by the MDN method and the random sampling methodThe blue areas are results of the MDN method,and the red crosses are results of the random sampling method.(a)Joint probability distribution of the inner core radius and the outer core radius.(b)Joint probability distribution of radii of the outer core and the LVZ (Low-Velocity Zone).(c)Joint probability distribution of P-wave and S-wave velocities of LVZ.

为了评价MDN方法得到月球内部结构模型参数的精度，需要研究这些月球内部结构模型对应的模拟观测值与实际观测值的符合程度.对MDN方法得到月球内部结构模型后验概率分布进行1000次独立采样，同样利用正演方法计算它们对应的模拟观测值.图4给出了这些模拟观测值与实际观测值的比较，其中橙色竖线是实际观测值，橙色横线是其误差范围.图4a中平均密度模拟观测值的平均值为3345.64 kg·m-3,标准差为0.31 kg·m-3，与实际观测值3345.56±0.4 kg·m-3相比差别非常小，模拟观测值的平均值偏差与标准差的和(0.39 kg·m-3)在实际观测值的误差范围以内，说明反演结果对应的模拟观测值相对于与实际观测值的偏离程度以及反演结果的离散程度在误差允许范围内.图4b中平均转动惯量MOI的平均模拟观测值为0.393100，标准差为0.000029，其实际观测值为0.393112±0.000012，因此反演结果对应的平均值相对于实际观测值的偏差(0.000012)在误差范围内，然而反演结果对应的标准差要大于1倍中误差.图4c中勒夫数k2模拟观测值的平均值为0.0228，标准差为0.0008，其实际观测值为0.0220±0.0017；与实际观测值相比，模拟观测值平均值有0.0008的偏离，但是这个偏离加上标准差(0.0016)小于实际观测值的一倍中误差.造成三个模拟观测值精度与实际精度不一致的主要原因是MDN方法的目标函数是月球内部结构模型参数的似然函数，如公式(5)所示，并未利用任何观测值的精度信息.

图4 MDN方法获得的月球内部结构模型对应模拟观测值的统计直方图橙色实线表示实际观测值以及其误差范围．(a)平均密度;(b)平均转动惯量;(c)勒夫数k2.Fig.4 The statistical histogram of the simulated observation values corresponding to the lunar model obtained by the MDN methodThe orange solid lines are the real observations and their error range.(a)Mean density;(b)Mean solid MOI;(c)Love number k2.

MDN方法的反演结果是月球内部结构模型的后验概率密度分布，对于所有满足该分布的月球内部结构模型的模拟观测值而言，它们与观测值中的平均密度以及勒夫数k2的符合程度较好；而对于观测值中的平均转动惯量而言，它们的平均值的符合程度较好，而标准差则稍大于实际误差范围.但是本文给出的平均月球内部结构模型(Mean模型)和最大后验概率密度模型(MAP模型)对三个实际观测值观测误差都符合，进一步说明本文给出的最优化月球内部结构模型满足了所有观测值的观测误差.

2.2 月球内部结构模型的反演结果

表2给出了月球内部结构模型参数先验变化区间以及反演结果，其中Mean模型是服从后验概率密度分布月球内部结构模型的期望，它是所有反演得到月球内部结构模型的平均值；MAP模型是最大后验概率密度对应的月球结构模型，它是所有反演得到月球内部结构模型当中可能性最大的模型.两个模型相差很小，原因是反演得到的后验概率密度分布是一个简单的单峰分布，因此可以将MAP模型当作反演得到的最优化月球结构模型.“1-σ”一列是在1-σ准则下月球内部结构模型参数的变化范围，它对应着在Mean模型参数附近概率密度积分为68.26%的区域内所有月球内部结构模型.

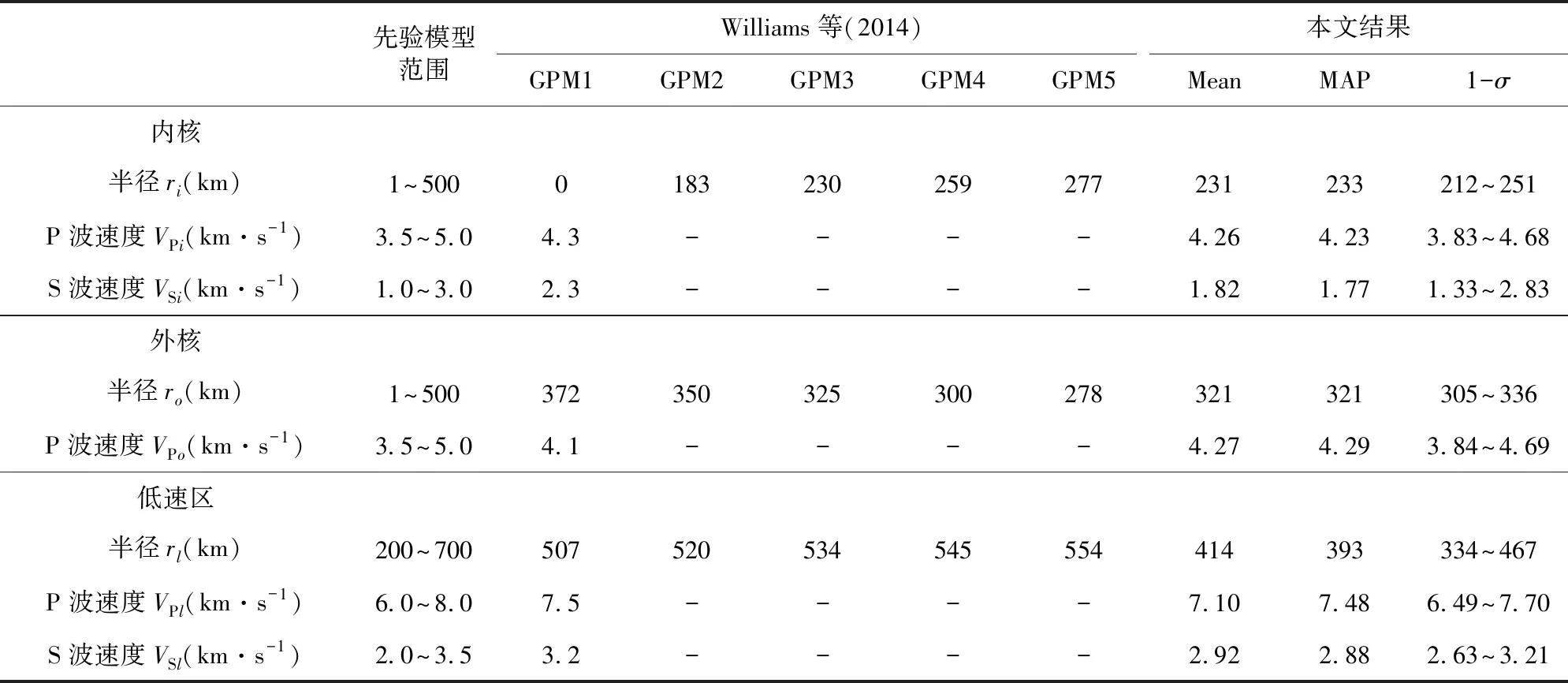
表2 月球内部结构模型参数先验变化区间和反演结果Table 2 The priori variation intervals and inversion results of the lunar internal structure model parameters

图5是月球内部结构模型中各层半径、P波和S波速度的垂直剖面图，其中灰色线条表示Weber等(2011)的月球内部结构模型，蓝色虚线表示表2中的MAP模型.在图5a中的红色误差棒表示表2中1-σ模型中的低速区、外核以及内核半径的变化范围，它们值分别为212～251 km、305～336 km、334～467 km.Matsuyama等(2016)给出1-σ准则下的半径变化范围分别为6～275 km，194～362 km，345～505 km.本文结果与他们的结果相比，给出的变化区间更窄，这是由于本文假设月球结构模型中的密度以及低速区LVZ以外圈层的其他模型参数均为定值，而在Matsuyama等(2016)的工作中这些参数都是变量，因此模型的不确定性更大.图5(b，c)表示P波速度VP以及S波速度VS的垂直剖面，其中红色虚线的区间表示表2中1-σ准则下P波速度与S波速度的变化范围.Matsumoto等(2015)给出低速区内的P波及S波速度分别为7.1±1.0 km·s-1、2.9±0.5 km·s-1；本文1-σ准则下给出的6.49～7.70 km·s-1、2.61～3.21 km·s-1与Matsumoto等(2015)的结果相比区间更窄，原因与上面半径类似.MDN方法的反演结果与前人的反演结果基本吻合，但是由于简化了反演参数个数，因此本文反演的模型不确定度小于前人的结果.此外Matsuyama等(2016)的结果显示低速区LVZ存在的可能性约为50%，本文结果给出的低速区S波速度为2.63 ～ 3.21 km·s-1，明显低于Weber等(2011)的月幔S波速度4.50 km·s-1，因此本文结果支持月幔底部存在低速区的观点.

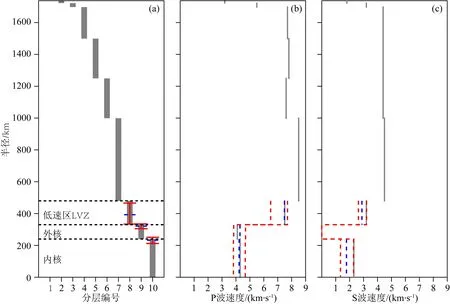
图5 月球内部结构模型各层半径(a)、P波(b)及S波(c)速度的垂直剖面灰色实线为Weber等(2011)的月球内部结构模型，左图中红色的误差棒和右边两图的红色虚线为本研究中1-σ准则下月球内部结构模型变化区间，蓝色虚线为MAP模型.Fig.5 Vertical profiles of the radii (a),P-wave (b)and S-wave (c)velocities of lunar modeled layersThe gray solid lines are the lunar model given by Weber et al.(2011).The red error bars in the left figure and the red dotted lines in the two right figures are the ranges of the lunar model under the 1-σ criterion in this study.

利用模型参数间的联合概率密度分布可以对模型参数之间的相关性进行研究.图6给出了利用MDN方法得到的内外核半径以及外核半径与低速区半径的联合概率密度分布，其中黄色菱形表示表2中MAP模型,红色五角星则对应于Williams等(2014)的月球内部结构模型GPM 1—5，其数值见表2.如2.1节所述，内外核半径之间存在明显的线性负相关关系，这是平均密度、平均转动惯量以及勒夫数k2的观测值与误差范围共同作用的结果.从2.3节的研究结果来看，在三个观测值现有的观测误差范围内，k2允许模型参数在较大的范围内变化，因此它对模型参数的约束较弱，因此月球内部结构模型的变化范围主要受到平均密度和平均转动惯量约束.在本研究问题的假设背景下，低速区密度(3.4 kg·m-3)与月幔相同，因此低速区半径的改变对平均密度和平均转动惯量没有任何影响，而月核中内核密度(8.0 kg·m-3)大于外核密度(5.1 kg·m-3).因此为了保持平均密度不变，二者的半径必然存在线性负相关关系；此外对于平均转动惯量，由于采用的是归一化的数值，因此其变化趋势与平均密度一致.内外核半径联合概率密度分布的结果与GPM 2—5模型符合程度较好，并且Mean模型和MAP模型几乎与GPM 3模型重合.而月球内部结构模型中的低速区半径低于GPM 1—5模型，造成这种差异的主要原因是所采用的固体潮勒夫数k2为Matsuyama等(2016)给出的0.0220±0.0017，而非Williams等(2014)采用的0.02422±0.00022,该结果进一步说明了固体潮勒夫数k2的观测值及其精度对月球内部结构模型影响较为显著.

图6 月球内部结构模型参数联合概率密度分布(a)内核半径与外核半径；(b)外核半径与低速区半径.黄色菱形为MAP模型,红色五角星分别对应了月球内部结构模型GPM 1—5．Fig.6 Joint probability density distribution (JPDD)of lunar model parameters(a)The JPDD of the inner core radius and the outer core radius；(b)The JPDD of the outer core radius and the LVZ radius.The yellow diamond refers to the MAP model and the red stars are lunar models GPM 1—5,respectively.

2.3 观测值精度对反演的月球内部结构模型的影响

与其他反演方法相比，MDN方法除了可以得到月球内部结构模型的后验概率密度分布之外，还可以得到观测值与月球内部结构模型参数的函数关系，这种函数关系为我们评估观测值精度对所反演月球内部结构模型的影响提供了可能.

图7给出了在平均密度与平均转动惯量为定值(取值如表1所示)条件下，勒夫数k2与月球内部结构模型参数之间的关系.橙色实线为MDN方法得到的Mean模型与勒夫数k2的函数关系，蓝色实线是利用正演数值计算方法得到二者函数关系.MDN方法与正演数值计算方法结果的差异反映了MDN方法作为一种函数近似方法的近似误差.在一倍观测误差(0.0017)以内，函数的梯度有着明显的变化，模型参数与勒夫数k2之间函数关系呈现出明显的非线性．在Williams等(2014)给出的固体潮勒夫数k2=0.02422±0.00022附近，内核半径与外核半径的斜率趋近于0，而低速区半径的斜率则是一个较大的正数，因此勒夫数k2在误差范围内的变化对低速区半径的精度影响较大，而对内外核半径的精度影响较小.而对于Matsuyama等(2016)给出的固体潮勒夫数0.0220±0.0017而言，勒夫数k2的观测误差对上述三个模型参数精度的影响程度相当.此外由于内外核半径以及低速区半径存在ri

图7 月球内部结构模型参数与勒夫数k2的函数关系(a)内核半径；(b)外核半径；(c)低速区半径.Fig.7 Function relationship between lunar model parameters and the Love number k2(a)Radius of the inner core；(b)Radius of the outer core；(c)Radius of the LVZ.

图8给出了观测误差为0时，利用MDN方法以及表1中的观测数据得到月球内部结构模型的后验概率密度分布，其中红色五角星为GPM1～5模型.图8中内外核半径以及低速区半径均在275 km附近，而2.2节中的平均月球内部结构模型Mean内核半径为231 km，外核半径为321 km，低速区半径为414 km.造成二者差异的原因主要是因为观测值k2=0.0220趋近于其取值范围的下边界，因此对于Matsuyama等(2016)给出的固体潮勒夫数k2=0.0220±0.0017,其有效变化范围为k2=0.0220～0.0237，如果k2为0.0220时反演结果表明内核半径为275 km而外核与低速区厚度为0，而如果k2为0.0237时反演得到内核半径为218 km，外核半径为318 km,低速区半径为480 km；在假设k2服从均匀分布的条件，其平均值为0.02285，则反演结果便如图6中所给出.这也是图4反演结果中勒夫数k2模拟观测值平均值相对于实际观测值有明显偏离的主要原因.

表3 观测值在其误差范围内变化时导致的月球内部结构模型参数变化幅度
Table 3 Variation range of lunar model parameters caused by variations of observations within their errors

观测值精度对月球内部结构模型的影响主要由两个方面决定：第一个方面是问题的物理背景，月球内部结构模型参数通过正演过程得到对应的模拟观测值，因此模拟观测值与模型参数之间通过控制方程建立起如图7所示的函数关系.在不同观测值附近函数斜率不同，因此月球内部结构模型对模拟观测值的敏感程度也不同.第二个方面是实际观测值的概率密度分布.如果实际观测值观测误差为0，那么反演得到的模型参数会是一个准确值；而当用概率模型描述观测值的精度时，实际观测值并不是常数而是一个随机变量.实际观测值作为随机变量在误差范围内变化时，对应的模型参数会在函数的某一段区间内上下浮动，其变化幅度的大小取决于误差范围的大小以及函数在各点上的斜率.

从图7可以看出勒夫数k2与模型参数的函数在其误差范围内具有明显的非线性，因此利用函数在观测值处的斜率分析模型参数可能的变化范围是不合理的.此外考虑到其他模拟观测值与模型参数的函数可能是非单调性的，因此用在观测值误差范围内模型参数最大值与最小值的差来度量模型参数的变化范围是一种更为合理的方法.为了比较不同观测值对模型精度的影响，在其他两个观测值为确定值的条件下，计算单个观测值在其误差范围内变化时对应月球内部结构模型参数的变化幅度.表3给出了三个观测值在各自一倍中误差范围内对应月球内部结构模型参数的变化幅度.表3结果显示在观测值的误差范围内，勒夫数k2对应的月球内部结构模型参数变化幅度远远大于其他两个观测值，例如对于低速区S波速度而言，勒夫数k2的影响幅度为202.79 m·s-1，约是MOI影响幅度1.91 m·s-1的200倍；对于其他月球内部结构模型参数而言，k2的影响同样远大于MOI和平均密度的影响.

内核外核低速区半径ri(km)P波速度VPi(m·s-1)S波速度VSi(m·s-1)半径ro(km)P波速度VPo(m·s-1)半径rl(km)P波速度VPl(m·s-1)S波速度VSl(m·s-1)勒夫数k260.5952.9735.3648.4319.46198.50105.42202.79平均转动惯量MOI0.357.681.430.281.030.354.691.91平均密度ρ(kg·m-3)2.5927.66.072.183.62.3821.03.21

3 结论

利用混合密度神经网络(MDN)方法以Williams等(2014)基于GRAIL任务给出的月球平均密度和平均转动惯量、Matsuyama等(2016)给出的月球弹性勒夫数k2作为观测约束，对月球内外核以及低速区的半径、P波和S波速度共计8个参数进行了反演，得到了月球内部结构模型的后验概率密度分布，获得了最优化月球内部结构模型，即最大后验概率密度对应的MAP模型.除此之外还计算了后验概率密度分布的平均月球内部结构模型(Mean模型)以及基于1-σ准则给出的月球内部结构模型范围.Mean模型与MAP模型差别较小且后验概率密度分布是单峰分布说明以MAP模型作为最优化月球内部结构模型是合理的.反演得到的月球内部结构模型中，内核半径与外核半径呈现出明显的线性负相关关系，这是因为在三个观测值观测精度内勒夫数k2允许模型参数在较大的区间内变化，而与之相比平均密度和平均转动惯量在误差允许范围内几乎可以认为是不变的.反演结果中低速区S波速度(2.63～3.2 km·s-1)明显低于月幔S波速度(4.50 km·s-1)，因此本文结果支持月幔底部存在低速区.

相比于其他反演方法，MDN方法的优势主要体现在三个方面：(1)与传统的最小二乘法反演方法相比，MDN方法可以解决反演的不唯一性与非线性性；(2)与反演中经常采用的蒙特卡洛方法相比，MDN方法避免了“维度诅咒”，因此计算效率更高；(3)MDN方法不仅可以获得一个实际观测值对应的月球内部结构模型参数，还可以获得实际观测值与月球内部结构模型参数之间的函数关系，为进一步分析不同观测值观测误差对月球内部结构模型的影响提供了可能.

通过研究勒夫数k2与模型参数间的函数关系，数值结果表明勒夫数k2存在一个约为0.022的下限值.利用在观测误差范围内模型参数的变化分布作为度量，研究了不同观测值精度对模型的影响，结果显示现有观测精度条件下勒夫数k2的精度对月球内部结构模型的影响明显要大于其他两个观测值.在将来的月球观测任务中，期望能首先考虑提高固体潮勒夫数的观测精度，这样就能对月球内部结构进行更加准确的约束.