代丽芳， 梁茂林

天水师范学院 数学与统计学院， 甘肃 天水741001

张量是数值多重线性代数的主要研究对象， 其在量子力学、 心理测量学、 化学计量学、 信号处理、 高阶统计等领域有重要应用[1-3]． 张量是向量和矩阵的高阶推广， 它的许多性质与矩阵情形类似， 但也有很大不同[4]． 张量相关问题的研究要比矩阵情形复杂得多． 目前， 在张量分解、 张量的低秩逼近、 张量互补问题、 张量特征值问题和张量方程等方面已有诸多研究成果[4-9]． 本文考虑基于Einstein积[10]的一类张量方程的求解问题．

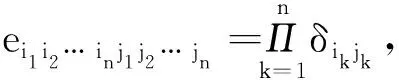
若张量A=(ai1i2… imj1j2… jn)∈CI1×I2×…×Im×J1×J2×…×Jn，B=(bj1j2… jnk1k2… kp)∈CJ1×J2×…×Jn×K1×K2×…×Kp， 则它们的Einstein积A*nB为I1×I2×…×Im×K1×K2×…×Kp-维张量， 依据文献[7]定义其元素为

进一步， 设张量S=(ai1i2… imj1j2… jn)，T=(bk1k2… kml1l2… ln)且S，T∈CI1×I2×…×Im×J1×J2×…×Jn， 则其内积定义为

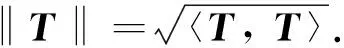
定义1设张量A=(ai1i2… imj1j2… jn)∈CI1×I2×…×Im×J1×J2×…×Jn， 则其共轭转置AH定义为

若张量A∈CI1×I2×…×Im×I1×I2×…×Im满足条件AH=A， 则称之为Hermitian张量．

若定义1中A是实张量， 则共轭转置退化为转置[7]． 值得一提的是， 最新的研究发现， Hermitian张量在量子纠缠中有实际应用[11]． 本文考虑张量方程

A*nX=B

(1)

的Hermitian解， 这里A，B∈CP1×P2×…×Pm×I1×I2×…×In为已知张量，X∈CI1×I2×…×In×I1×I2×…×In为未知的Hermitian张量． 张量方程(1)在控制系统、 连续力学等领域有实际应用[7，11]． 例如， 对于2-维泊松方程

Ω={(x，y)|0≤x，y≤1}， 利用中心差分格式， 可以离散为张量方程[7]

A*2U=F

(2)

这里张量A∈RN×N×N×N的非零元为

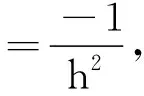
F∈RN×N， 对于没有约束条件的张量方程(1)， 文献[7]引入了张量逆的概念， 得到了它的最小二乘解． 进一步， 作为张量逆的推广形式， 文献[12]提出了张量的Moore-Penrose广义逆， 并讨论了张量方程(1)的可解性及其通解形式．

在图像处理等领域的应用中， 考虑方程解的特殊结构是降低算法复杂度的重要途径[13]， 但是对于带有约束条件的形如方程(1)的张量方程求解问题尚无研究． 借助张量的Moore-Penrose广义逆的性质， 我们将建立张量方程组(1)有Hermitian解的充要条件， 并得到有解时的一般解表达式． 进一步， 将考虑张量方程(1)约束下的张量逼近问题．

(3)

其中Θ表示张量方程(1)的所有Hermitian解的集合．

1 主要结果及证明

为了研究Hermitian张量约束下的张量方程(1)的求解问题， 我们首先引入如下引理， 这对得出本文的主要结果是十分重要的．

引理1[19]设F∈CI1×I2×…×Im×J1×J2×…×Jn，G∈CK1×K2×…×Kp×L1×L2×…×Lq，E∈CI1×I2×…×Im×L1×L2×…×Lq， 则张量方程F*nZ*pG=E有解当且仅当F*nF+*mE*qG+*pG=E， 此时它的通解为

Z=F+*mE*qG++Y-F+*mF*nY*pG*qG+

其中张量Y∈CJ1×J2×…×Jn×K1×K2×…×Kp是任意的．

引理2设张量A，B∈CP1×P2×…×Pm×I1×I2×…×In， 则张量方程(1)有Hermitian解的充要条件为张量方程组

(4)

有一般解．

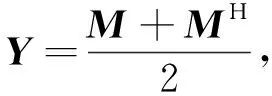
由引理2可见， 求解张量方程(1)的Hermitian解等价于求解张量方程组(4)的一般解． 基于此， 我们得到如下定理．

定理1设张量A，B∈CP1×P2×…×Pm×I1×I2×…×In， 则张量方程(1)有Hermitian解的充要条件为

A*nBH=B*nAH，A*nA+*mB=B

(5)

此时它的一般解为

(6)

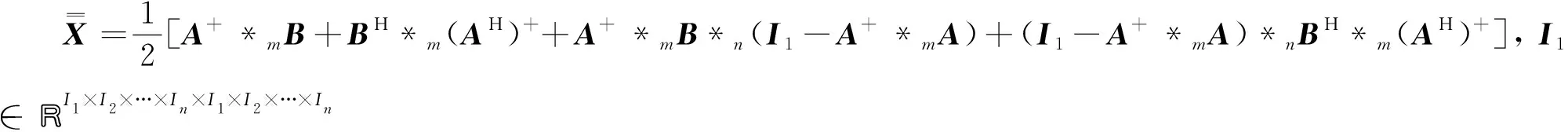
证根据张量Moore-Penrose广义逆的性质和引理1可知， 张量方程(1)有解的充要条件为

A*nA+*mB=B

(7)

此时

X=A+*mB+(I1-A+*mA)*nZ

(8)

这里Z∈CI1×I2×…×In×I1×I2×…×In为任意张量． 当式(7)成立时， 结合式(4)可知A*nBH=B*nAH， 即知式(5)成立．

进一步， 将式(8)代入式(4)的第二个方程X*nAH=BH并整理得

(I1-A+*mA)*nZ*nAH=BH-A+*mBnAH

这是关于变量Z的张量方程． 在条件(7)成立时， 该方程总是有解的， 且由引理1知其一般解为

(9)

其中W∈CI1×I2×…×In×I1×I2×…×In为任意张量． 将式(9)代入式(8)可得

结合引理2的证明过程可得式(6)成立． 命题得证．

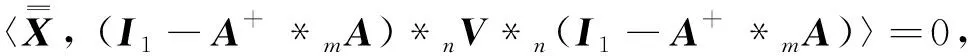
接下来考虑张量的最佳逼近问题(3)． 首先引入如下引理．

引理3[19]设E∈CI1×I2×…×Im×J1×J2×…×Jn，F∈CI1×I2×…×Im×I1×I2×…×Im，G∈CJ1×J2×…×Jn×J1×J2×…×Jn且满足

F*mF=F=FH，G*nG=G=GH

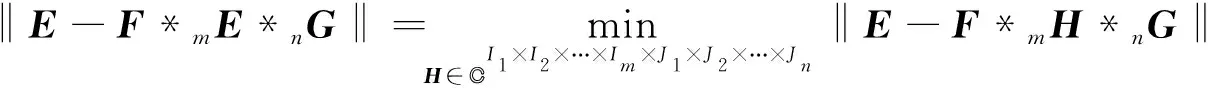
根据引理3， 我们可以证明张量逼近问题(3)的解是唯一的， 并给出解的具体形式．

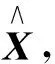
(10)

成立， 此时

(11)

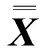
证当定理1中的条件(5)成立时， 张量方程(1)的解集合Θ是非空的， 且容易验证它是一个闭凸集， 这说明最佳逼近问题(3)有唯一解． 由式(6)和式(3)可得

(12)

因为I1-A+*mA为正交投影张量， 故满足引理3中的假设条件， 从而有

(13)

当且仅当

(14)

由式(12)和式(13)可得式(10)， 而式(6)和式(14)说明最佳逼近问题(10)的唯一解为

(15)

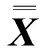
2 数值试验

本节通过数值例子验证所得结论的可行性． 接下来的所有实验数据均是通过配置了Inter(R) Core(TM) i5-4200M CPU与4.00 G内存的电脑上的MATLAB软件编程实现， 其中张量积的运算用到了张量工具包[20]．

例考虑离散的2-维泊松方程的Hermitian解， 即张量方程(2)， 这里取张量F=eyes(N，N)为单位张量． 另外， 给定张量U0∈RN×N随机产生， 即U0=randn(N，N)， 容易验证， 已知张量A和F满足定理1中的条件(5)， 故相应的张量逼近问题

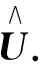
图1 给定张量及最佳逼近解

3 总结

本文考虑了基于Einstein积的张量方程A*nX=B关于Hermitian张量X的可解性问题． 利用张量Moore-Penrose广义逆的性质， 得到了上述问题有解的充要条件， 并得到了它的一般解表达式． 另外， 对于任意给定张量， 在假定上述条件成立时， 讨论了相应的张量最佳逼近问题， 证明了解的唯一性， 并得到了它的具体表达式． 最后给出实际应用实例验证了本文所得结果的可行性， 这些结果对张量相关理论的完善具有重要意义．