魏文军 尉晶波

(1.兰州交通大学自动化与电气工程学院,甘肃兰州 730070;2.兰州交通大学光电技术与智能控制教育部重点实验室,甘肃兰州 730070)

1 引言

多智能体系统的一致性控制由于其广泛的应用,如无人机编队控制[1-2],自主移动的智能体群[3]等,引起了广泛的关注.一般而言,多智能体系统的一致性问题分为无领导者一致性[4]和有领导者跟随一致性[5].无领导者一致性是为每个智能体设计一致性控制律,通过智能体间的局部通信,使智能体最终趋于一致.有领导者跟随一致性是指一个智能体作为领导者,其余智能体作为跟随者.领导者作为指令发出者,生成参考轨迹,跟随者通过智能体间的局部通信跟踪到领导者信号,实现多智能体的跟踪一致性.

多智能体最优一致性控制是多智能体一致性控制的一个重要的分支,在实际工程应用中有着重要的意义.最优控制是指在满足系统稳定性条件下,使得系统的性能指标取得极值.文献[6-8]提出了一种通过求解线性二次调节器(linear quadratic regulator,LQR)问题的分布式最优控制设计方法,虽然解决了多智能体系统的最优控制问题,但系统达到稳态的时间长.针对具有输入约束的一般线性多智能体系统的最优一致性控制问题,文献[9]利用逆最优方法提出了基于滚动时域控制的一致性策略,设计了最优一致性协议.文献[10]利用逆最优方法研究了线性多智能体系统中各智能体状态可测的最优一致性控制问题.文献[11-12]提出了一种基于模糊自适应动态规划的最优控制算法,解决了多智能体系统的一致性最优控制问题.文献[13]提出了一种基于神经逆最优控制的控制律设计方法,解决了非线性离散多智能体系统的分散镇定控制问题.文献[14]为解决非线性离散多智能体系统的分布式逆最优控制问题,提出了一种基于非合作博弈的协同控制方法.而对于全局最优控制问题,通常需要智能体的全局信息,在实际应用中很难获得智能体的全局信息.在文献[15]中,为每个智能体设计了分布式近似最优控制器,解决了系统的分布式最优控制问题.文献[16]为解决异构非线性多智能体系统的最优控制问题,通过分布式观测器为每个智能体提供领导者信息,利用无模型近似动态规划算法提出了一种最优分布式控制协议.文献[17]考虑了指定性能和带有输入死区约束的严格反馈非线性系统,提出了自适应模糊最优控制算法,使系统的跟踪误差约束在指定范围内.文献[18]研究了一类不确定的严格反馈非线性系统的自适应模糊反优化控制问题,利用反步递归算法提出了自适应模糊逆向优化方案,保证系统从输入到状态的稳定性,并且在目标函数方面实现反优化.文献[19]研究了一般线性多智能体系统的逆最优控制问题,提出了基于静态输出反馈的最优协同控制协议.

在实际应用中,智能体控制性能的好坏对系统整体的运行有重要的意义,比如瞬态性能、稳态性能和最优性能,其中系统的瞬态性能依赖于系统特征值的位置.针对这一点,文献[20]引入两个关于闭环系统特征值的性能指标来评价一致性性能:收敛率和阻尼率.收敛率用于评价智能体的收敛速度,阻尼率用于评价智能体的振荡行为.然而,现有的基于LQR的一致性设计方法[6-8,21]在解决这类问题时存在重大缺陷,因为很难选择合适的权重矩阵,使得多智能体系统的特征值不能位于特定的区域,从而很难获得理想的一致性性能.

上述文献虽研究解决了多智能体系统的最优控制问题,但这些文献解决智能体控制性能的同时没有考虑系统整体性能最优.主要存在以下问题:1)研究对象主要为线性或非线性离散多智能体系统,所提的研究方法无法满足一般连续非线性多智能体系统;2)仅仅考虑了系统的整体最优性能,单个智能体的控制效果一般且收敛时间长,无法满足对单个智能体性能要求高的系统.

基于上述讨论,本文针对一般连续非线性多智能体系统,研究拓扑切换下的全局最优协同控制问题.主要的创新点如下: 1)提出了通过一种IT2 T-S模糊模型将连续非线性系统等价转化为线性系统;2)基于局部稳定性理论,给出了全局逆最优控制的充要条件和全局逆最优控制的设计过程;3)基于全局逆最优控制条件,设计了拓扑切换下全局最优控制律,使得多智能体系统实现期望性能下的全局最优控制,同时实现了单个智能体的期望性能,解决了现有文献中控制效果一般和系统达到一致时间长的问题.

2 图论

考虑具有N个节点的非空有限集的加权有向图G=(V,E,A),其中V(ν1,ν2,...,νN),边集E ⊂V×V,相关的邻接矩阵A[aij]RN×N.始于根节点j并终止于节点i的边缘用(νj,νi)表示,这意味着信息从节点j流向节点i,边(νj,νi)的权重aij为正.即若(νj,νi),则aij ＞0,否则,aij0.在本文中,假设没有重复的边和自闭环,即aii0,∀i{1,2,...,N}.若(νj,νi),则节点j称为节点i的邻接节点.节点i的邻接节点集表示为Ni{j|(νj,νi).定义有向图的入度矩阵Ddiag{diRN×N,其中di定义拉普拉斯矩阵LD-A.若图G中两个节点可以通过一条路径连起来,则称图G为连通图.若图G中的每两个顶点都可以有一条有向路连接,则称图G为强连通图.若图G为强连通图,其含有一个零特征值.图G含有一个有向生成树,则存在从节点i到图中每个其他节点的有向路径.

3 非线性多智能体系统

本文考虑非线性多智能体系统由N个非线性子系统组成.第i个非线性子系统的动态方程为

其中:i1,2,...,N,N为非线性智能体的个数;AiRm×m为系统状态矩阵;BiRm×n为系统输入矩阵;xi(t)Rm为第i个子系统的状态列向量;ui(t)Rn为第i个子系统的控制输入向量;fi(.):Rm →Rm非线性函数.

为了表示非线性系统的局部线性输入/输出关系,应用一种局部线性输入输出关系模型[4]-IT2 T-S模糊模型.非线性系统可根据IT2 T-S模糊模型转化为下列局部线性子系统:

其中:EilRm×m,l1,2,...,r,r为模糊规则数.xi[xi1xi2...xim]T;ui[ui1ui2...uin]T.

局部线性子系统式(2)的全局方程为

利用单点模糊化,乘积模糊推理和加权平均数模糊化,IT2 T-S模糊系统将式(1)可写为式(4)

其中隶属度函数

系统式(3)的全局动态方程为

不失一般性,推导本文结论前,对IT2 T-S模糊化的多智能体系统做出以下假设:

假设1(Bil)是可控的.

假设2图G含有一个有向生成树.

分别对有领导者和无领导者情况下当智能体能够获取邻接智能体的状态信息,基于LQR方法[21]设计的全局状态反馈控制器

使得多智能体系统的全局目标函数(9)最小.

其中:Kl为局部线性子系统全局反馈增益;Ql,Rl为已知的对称非负定矩阵;反馈增益矩阵

其中Pl为Riccati方程式(10)的唯一正定对称解.

式(10)可等价为

则S为李雅普诺夫渐进稳定的.

由引理2可推出下列命题.

命题1若以下条件成立

2)Kl是稳定的到Pl的零空间;对于逆最优控制问题,Kl是最优的和Pl为Riccati方程的半正定解.

证由式(11)可得

考虑以下性能指标:

命题2对于逆最优控制问题,Kl是最优的;当Ql≥0和Rl≥0时,Pl为Riccati方程的唯一半正定解,当条件成立

1)Kl/2是稳定的在Pl的零空间;

2)KlBl为半正定矩阵.

由上述证明可知,对任意x0Rm且x00时,系统性能指标的最优值为

4 多智能体系统全局逆最优控制律设计

不失一般性,设计全局逆最优控制律前,假设模糊

本文假设智能体i能够获取邻接智能体的状态信息,在此前提条件下研究有向拓扑切换下有领导者和无领导者的非线性多智能体系统全局逆最优协同控制问题.

4.1 有领导者多智能体系统全局最优控制

假设领导者和跟随着为同构智能体.领导者系统的动态方程如下:

其中:v0为领导者系统的状态向量,为领导者系统的状态矩阵.

设计局部子系统i的控制律uicKilεi,使得多智能体系统的所有节点都能同步于领导者节点,同时使得系统的二次型性能指标值达到最小.

定义线性子系统i邻接误差方程为

系统的全局邻接误差方程为

模糊化的多智能体系统的全局闭环方程为

多智能体系统的全局闭环误差方程为

引理3[10]设λi为矩阵(L+H)σ(t)的特征值.若全局闭环跟踪误差系统实现渐近稳定,当且仅当矩阵-cλiBlKl为Hurwitz.

定理1对于全局跟踪误差系统,设计分布式控制律式,当且仅当矩阵(L+H)σ(t)为正定矩阵,系统的全局二次性能指标达到最优.

证(必要性) 由命题3可知,若分布式控制律u-c(L+H)σ(t)⊗Klε为最优,矩阵[(L+H)σ(t)⊗Kl](In ⊗B)为正定矩阵.存在一个非奇异矩阵T1满足

其中Λ1为矩阵(L+H)σ(t)⊗(KlBl)的特征值对角阵.

矩阵(L+H)σ(t)和KlBl的约旦标准型分别为

将式(25)-(26)代入式(28)中,可得

由于系统的通信拓扑图G包含一个生成树,其中至少有一个非零增益连接到根节点.因此拓扑图G所对应的矩阵(L+H)σ(t)的全部特征值均有正实部.假设(L+H)σ(t)有共轭复根α±jβ,其中α ＞0,0R.假设µ为矩阵KlBl的一个非零特征值,则µ(α±jβ)为Λ1的特征值.可得µ(α±jβ)＞0.当µ＞0和β0时,矩阵(L+H)σ(t)为正定的.

(充分性) 设Kl[K1K2]Rn×m,矩阵

其中ΣSA11+A21-cλiB1K1-(SA12+A22-cλiB1K2)S.

当cλi ＞1,推导可知(x)＜0,因此-cλiBlKl为Hurwitz.根据引理2,选择S,F和c ＞cmin,使得系统为渐进稳定的.根据命题3可知,c(L+H)σ(t)Kl为最优反馈控制增益.

其中Pl为Riccati方程式(36)的唯一正定对称解.

证毕.

4.2 无领导者多智能体系统全局最优控制

对于无领导者多智能体系统的一致性问题,当时间t →∞,智能体的状态能够达到同一状态.即

通过设计分布式一致性控制律ui,使得系统的每个智能体达到同一状态,并使系统的性能指标达到最小.设计的无领导者局部线性子系统的全局分布式一致性控制律

其中:c ＞0,反馈增益矩阵KlRn×m.线性化的多智能体的闭环系统方程可写为

全局闭环系统可写为

假设系统的通信拓扑为强连通的,拓扑图对应的Laplace矩阵Lσ(t)的特征值λ10,其余的特征值均为有正实部的非零特征值.

定理2对于全局闭环系统(40),在分布式一致性控制律u作用下,系统的全局二次性能指标式(41)是最优的.

此外,由于全局逆最优分布式一致性控制律式(38)稳定在零空间Im ⊗Lσ(t),系统的通信拓扑为强连通拓扑,因此在最优控制律作用下,智能体系统能够实现一致性.

于是cLσ(t)⊗Kl可写为

下面证明cLσ(t)⊗Kl能够渐近稳定到Lσ(t)⊗In的零空间.

对角阵J3是由一个零特征值和n-1个正特征值构成的对角阵,即J3diag{0,λ2,...,λn}.由此可推导得出

根据引理1可知,cLσ(t)⊗Kl为渐近稳定到零空间Lσ(t)⊗In.因此,命题1中的条件均满足,无领导者分布式反馈控制律为最优的且渐近稳定,非线性多智能体系统中的每个智能体能够最终达到一致.证毕.

从实际角度来看,多智能体系统的一致性能够达到预期的期望值是非常有意义的.系统中的每个智能体的瞬态状态取决于系统闭环极点的位置.为了更好地使多智能体系统的一致性能够达到期望值,本文采用逆最优分布式反馈控制方法解决系统的一致性能够达到预期值.针对有无领导者非线性多智能体系统,给出逆最优分布式控制律设计步骤.

1) 无领导者系统.

步骤1:根据IT2 T-S模糊将非线性多智能体系统转化为多个局部线性子系统.

步骤2:根据智能体间的通信拓扑Lσ(t),求出对应的最小特征值并令c1/

步骤3:设计矩阵S使得A11-A12S的m-n个特征值{ω1,ω2,...,ωm-n}全部位于指定位置.

步骤4:根据式(34)求解反馈增益矩阵Kl并令γ→+∞.

步骤5:根据求得的反馈增益矩阵Kl确定系统的逆最优分布式控制律.

2) 有领导者系统.

步骤1:根据IT2 T-S模糊将非线性多智能体系统转化为多个局部线性子系统.

步骤2:根据智能体间的通信拓扑(L+H)σ(t),求出对应的最小特征值并令c1/

步骤3:设计矩阵S使得A11-A12S的m-n个特征值{ω1,ω2,...,ωm-n}全部位于指定位置.

步骤4:根据式(34)求解反馈增益矩阵Kl并令γ→+∞.

步骤5:根据求得的反馈增益矩阵Kl设计系统的全局逆最优分布式一致性控制律.

5 仿真算例

下面分别对有向拓扑切换下的有无领导者非线性多智能体系统的全局最优控制给出算例仿真,验证逆最优分布式反馈控制律的有效性和正确性.

5.1 无领导者系统

非线性系统由6个非线性智能体组成,智能体间的有向切换拓扑如图1所示,1 s为一个拓扑切换周期.

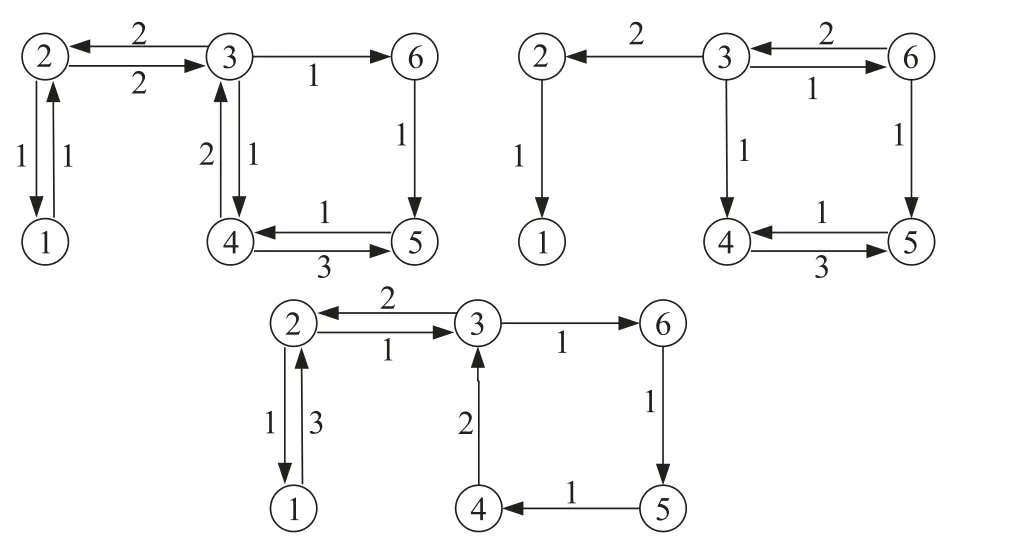
图1 系统的有向切换拓扑Fig.1 The system’s directional switching topologies

非线性系统动态方程如式(48)所示.

利用IT2 T-S模糊规则将非线性系统化为不同模糊规则下的线性子系统.线性子系统可写为

规则li1若xi2在0的微小邻域内,则

规则li2若xi2在±π/2的微小邻域内,则

模糊规则所对应的隶属度函数如式(51)所示.

系统的有向切换拓扑如图1所示,其对应的Laplace矩阵L的最小正特征值0.8340,可得出c1.1991.

1) 基于LQR分布式反馈控制律.

选择权重矩阵QI3和R1,根据式(10)求解最优反馈增益Kl.在控制律式(12)作用下,非线性多智能体系统的一致性如图2所示,系统误差如图3所示,所有的智能体在4.3 s达到一致.

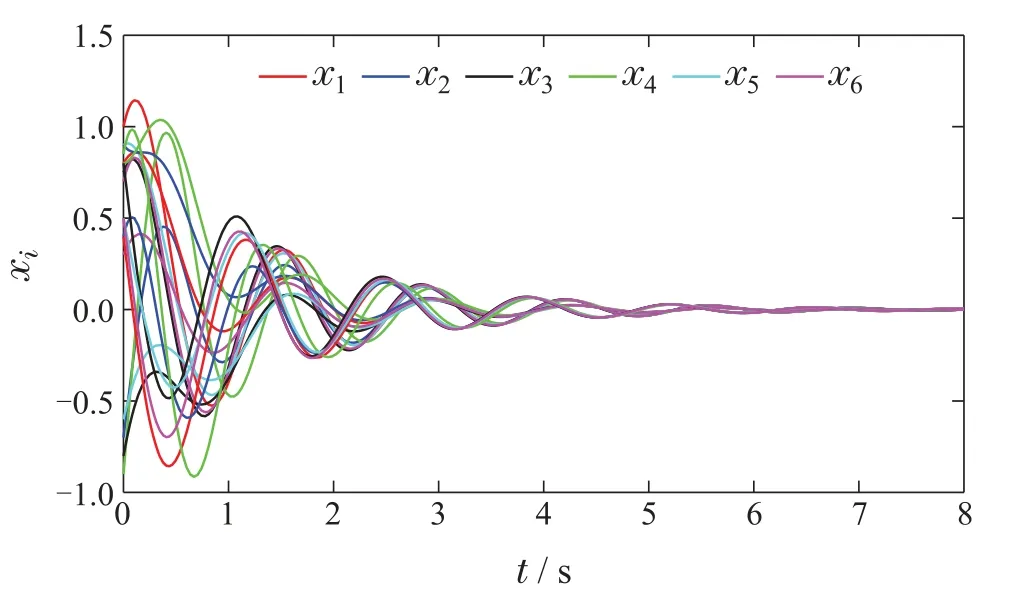
图2 基于LQR分布式反馈控制律下智能体状态Fig.2 Agent state under LQR distributed feedback control law

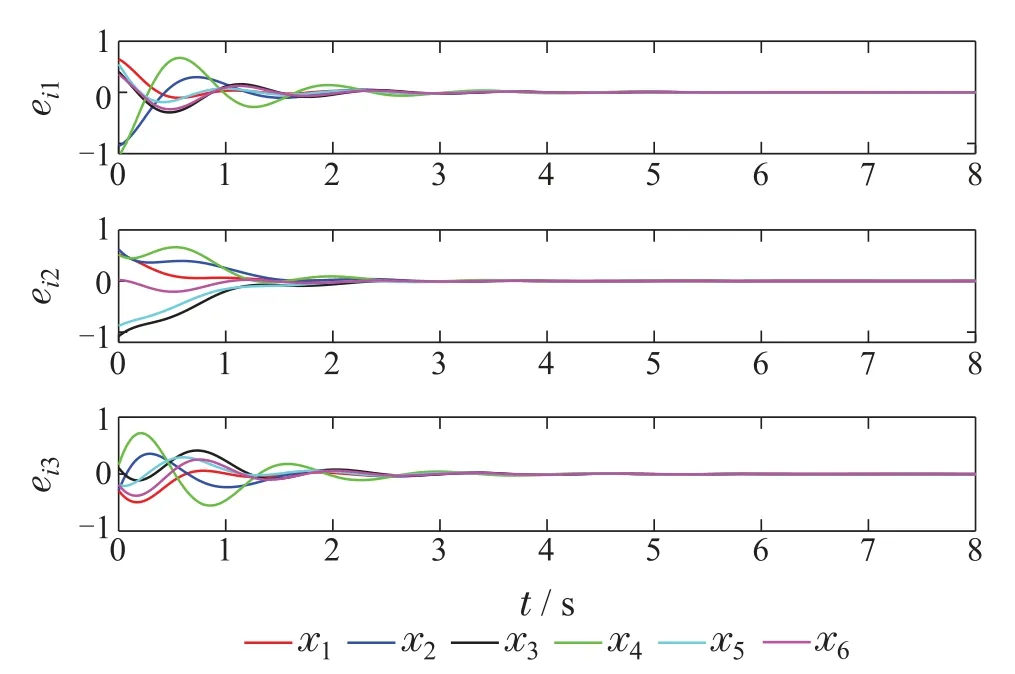
图3 基于LQR分布式反馈控制律智能体误差Fig.3 Agent error under LQR distributed feedback control law

2) 逆最优分布式反馈控制律.

设系统中A11-A12S对应的特征值为-3±j0.5,γ20.在逆最优控制律作用下,智能体的状态如图4所示,智能体间的误差如图5所示,所有的智能体大约在2 s达到一致,误差衰减为零.

图4 逆最优分布式反馈控制律智能体状态Fig.4 Agent state under Inverse optimal distributed feedback control law

通过图3和图5对比,基于逆最优方法设计的分布式一致性最优反馈控制律作用于多智能体系统时,非线性智能体达到一致所需时间明显缩短,对系统有很好的控制效果.

图5 逆最优分布式反馈控制律系统误差Fig.5 Agent state under Inverse optimal distributed feedback control law

5.2 有领导者系统

系统由6个非线性智能体和1个非线性领导者构成,通信拓扑如图6所示,拓扑切换周期为1 s.

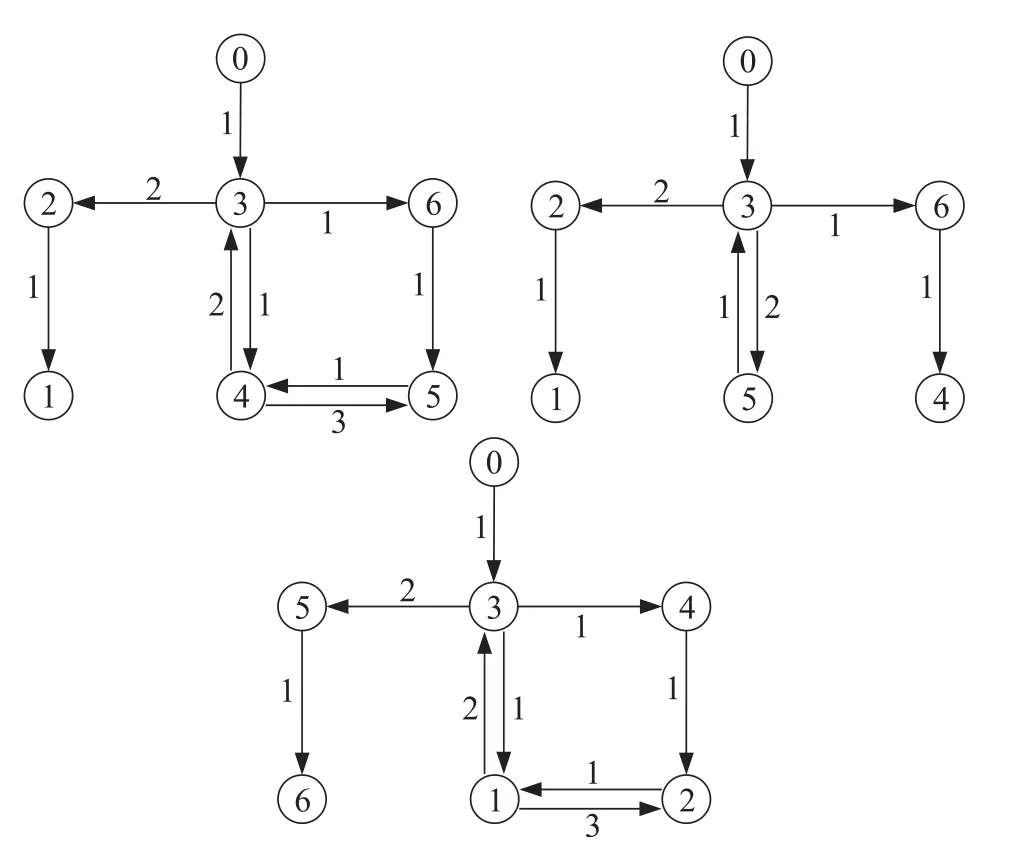
图6 系统的有向切换拓扑Fig.6 The system’s directional switching topologies

非线性领导跟随者多智能体系统的动态方程如式(48)所示.

非线性领导者系统方程如式(52)所示

通信拓扑网络图2对应的矩阵(L+H)σ(t)最小正特征值0.4544,则c2.2007.领导跟随者系统在不同控制律下的领导跟随一致性.

1) 基于LQR分布式反馈控制律.

选择权重矩阵QI3和R1,根据式(10)求解最优反馈增益矩阵Kl.在控制律式(12)作用下,非线性智能体的状态如图7所示,系统误差如图8所示,所有智能体大约在5 s时跟踪到领导者,误差衰减为零.

图7 基于LQR分布式反馈控制律智能体状态Fig.7 Agent state under LQR distributed feedback control law

图8 基于LQR分布式反馈控制律下智能体误差Fig.8 Agent error under LQR distributed feedback control law

2) 逆最优分布式反馈控制律.

假设A11-A12S对应的特征值为-2±j1.2,γ100,在逆最优分布式反馈控制律作用下,智能体的状态如图9所示,系统误差如图10所示,所有智能体在4 s达到一致,系统误差衰减为零,系统的一致性满足期望值.

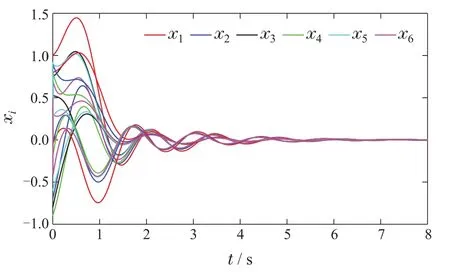
图9 逆最优分布式反馈控制律智能体状态Fig.9 Agent state under inverse optimal distributed feedback control law

对比图8和图10,有领导者非线性多智能体系统通过逆最优法设计的控制律对非线性多智能体系统有更好的控制效果,智能体跟随到领导者所需时间比一般控制律更短.

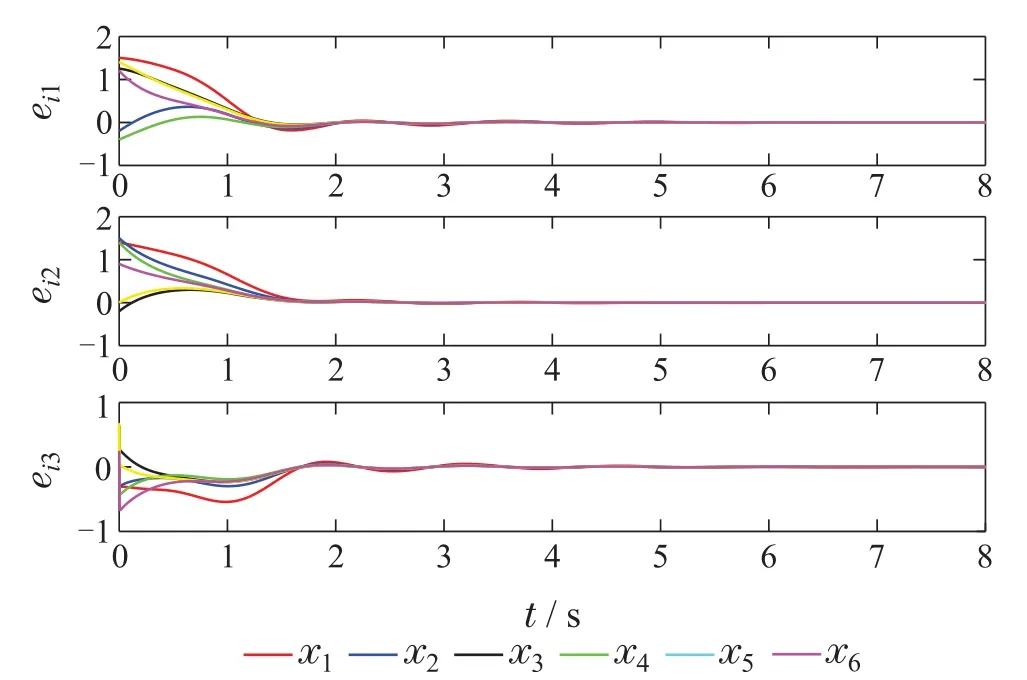
图10 逆最优分布式反馈控制律智能体误差Fig.10 Agent error under inverse optimal distributed feedback control law

6 结论

本文研究了拓扑切换下连续非线性多智能体系统全局逆最优控制问题,提出了用于一般连续非线性系统的方法,通过IT2 T-S模糊模型将非线性系统方程转化为线性系统方程;基于逆最优方法设计了拓扑切换下的一致性最优协同控制律,与基于LQR的方法相比,基于逆最优方法的最大优势在于: 1)对非线性多智能体系统有更好地控制效果,控制效果能够满足要求;2)智能体趋于一致或跟随到领导者所需时间更短,多智能体系统能够快速的达到期望值.