潘晓伟 刘忠信 陈增强

(1.南开大学人工智能学院,天津 300350;2.南开大学智能机器人技术重点实验室,天津 300350)

1 引言

纳什平衡问题(Nash equilibrium problems,NEP)由John Nash在文献[1-2]中正式提出.广义纳什平衡问题(generalized Nash equilibrium problems,GNEP)是NEP的拓展,由Gerard Debreu在文献[3-4]中正式提出,其特点是每个参与者的约束集合也依赖于其他参与者.GNEP在许多领域中都有所应用,如电信系统、环境污染控制等,参考综述文献[5].

近年来,基于算子分裂框架的求解方法正在得到越来越多的关注,其基本思路是将GNEP转化为算子的寻零问题,然后应用不同的算子分裂方法,可以得到相应的求解算法[6].基于两算子分裂方法的有: forward-backward(half)forward splitting[7-8,12],forward-backward splitting[9-10],forward-reflected-backward splitting[13]等.

基于forward-backward-forward splitting的算法[7],[8,算法2],每一轮迭代需要进行两次信息交换;基于forward-backward-half forward splitting 的算法[8,算法3],[12,Eqn.(6.11)]和基于forward-backward splitting的算法[9],需要假设伪梯度映射是强单调的,而另一基于forward-backward splitting的算法[10],则需要假设伪梯度映射是协强制的;基于forward-reflectedbackward splitting 的算法[13,算法5],其每一轮迭代只进行一次信息交换,而且只需要假设伪梯度映射是单调的和李普希茨的.

其他的求解算法有连续时间算法[11],邻近点算法(proximal point algorithm,PPA)[13,算法6],[14],交替方向乘子法(alternating direction method of multipliers,ADMM)[15]等.文献[11]中的算法要求伪梯度映射是严格单调的;文献[13]中的算法6只是针对一类具有特殊结构的聚合博弈设计的,其只需要假设伪次梯度映射是单调的;文献[14]中的算法需要假设代价函数是可导的,而在GNEP中会有非光滑项;文献[15]中的算法4.1经过变换之后,其实是一种forward-backward算子分裂方法.

根据上述内容可知,在基于算子分裂设计的方法中,要么对伪梯度映射均有较强的假设条件,要么每次迭代需要交换两次信息.

针对前述问题,本文的主要工作在于,基于三算子分裂算法forward-reflected-Douglas-Rachford(FRDR)算法[17],提出一种半分布式的FRDR算法.该算法有如下特性: 可以实现邻点映射和投影映射分别进行计算,因此更适用于分开计算时可以得出具体表达式的情形,而省去解决一个优化子问题;不需要假设伪梯度映射是协强制的或者强单调的;通过存储上一轮交换的信息,可以做到所需信息在每一轮迭代中只进行一次交换;同时,也给出了迭代残差的收敛速率,即o(1/(k+1)).跟本文算法比较相似的是基于forward-reflected-backward splitting的算法[13,算法5],区别在于FRDR 算法中邻点映射和投影映射的计算是分开进行的;此外,文献[13]中的算法5是针对聚合博弈设计的,而本文算法是针对一般的GNEP设计的.

本文的主要结构如下.第2节包括后续分析所需的预备知识以及对所研究问题的描述.第3节给出了半分布式FRDR算法的设计及其收敛性分析.第4节给出了仿真例子用来验证算法的有效性.最后是全文总结.

2 预备知识和问题描述

令Rm表示m维欧式空间,〈.,.〉是内积.Im表示m×m维单位矩阵.A ⊗B表示矩阵A和B的克罗内克积.对于向量x,‖x‖表示欧式范数;对于矩阵C,‖C‖表示导出范数.文中出现的向量,除非特别说明,均指列向量.(x1,...,xn)表示由列向量x1,...,xn等按列排列生成的列向量.diag{A1,...,An}表示由矩阵A1,...,An生成的分块对角阵.0m表示m维零向量.

2.1 算子理论及图论

集合S ⊂Rm是凸的,若,∀0＜α＜1,有αx+(1-α).intS表示集合S的内点.非空凸集S在处的法锥定义为NS(x):Rm|〈y-x,ξ〉≤0;若,则NS(x):∅.点R到非空闭凸集S的投影映射定义为projS(x):≤0.函数f:Rm →R是凸的,若其上图epif:{(x,u)Rm×R|f(x)≤u}是凸集,其次微分定义为∂f(x):Rm|f(y) ≥f(x)+Rm},其邻点映射定义为proxγf(x):

对于集值算子F:Rm⇉Rm,其图像定义为gphF:{(x,u)Rm×Rm|y F(x)}.算子F是单调的,若∀(x,u),(y,v)gphF,有〈x-y,u-v〉≥0是极大单调的,若F是单调的且不存在单调算子使得其图像能够真包含gphF是严格单调的,若∀(x,u),(y,v)gphF且,有〈x-y,u-v〉＞0是强单调的,若F -σId是单调的,其中σ ＞0.算子F的预解算子定义为JγF:(Id+F)-1,其中Id是单位算子.算子F的零点定义为zer(F):Rm|0(x)}.单值算子T:Rm →Rm是协强制的,若Rm,有〈x-y,T(x)-T(y)〉≥η‖T(x)-T(y)‖2,其中η＞0是李普希茨的,若Rm,有‖T(x)-T(y)‖≤ς‖x-y‖,其中ς ＞0.

以上内容均参照文献[18]给出.以下为图论相关内容.

智能体之间的通信拓扑可由G(V,E)描述,其中V{1,...,n}是顶点集合,E ⊂V ×V是连接边的集合.令cij≥0表示边(i,j)上的权重,若cijcji则表示G是无向图.定义图G的拉普拉斯阵为Lc:[lij]i,j∈V,其 中lij-cij,当;lii令µmax表示Lc的最大特征值.图G是连通的当且仅当Lc的零特征值是单根.

2.2 问题描述

考虑n个智能体参与的广义纳什平衡问题,智能体之间的通信拓扑为G(V,E).对于,其模型描述为

假设1对于,给 定x-i,fi(.,x-i)是 凸的,连续可导的,且其导数关于x是连续的;gi是正常且下半连续的凸函数;集合Si是闭凸集.

那么,在假设1和假设2成立的条件下,由文献[15]中的定理3.3和引理3.5可知,x*是v-GNE当且仅当,存在Lagrange乘子,满足

假设3伪梯度映射是单调的.

假设4智能体之间的通信连接图G是无向连通的.

那么,可以得到与文献[9]中定理2类似的结论.

引理1在假设1-4均成立的条件下,有如下结论:

1) 若

2) zer(G+F+C+NS×R˜mn×R˜mn)/∅.

引理1的证明与文献[16]中引理1的证明类似,此处不再给出.

3 算法设计与分析

为表示方便,令B:F+C,通过引理1,求解式(1)的v-GNE的问题可转化为求解满足0(w)+B(w)+的w.这是关于3个算子的寻零问题,因此,可以应用文献[17]中的算法进行求解

假设5伪梯度映射是ρ-Lipshitz连续的.

应用forward-reflected-Douglas-Rachford分裂算法[17]可得

关于v的更新律为

关于u的更新律为

消去vy和vλ,可得

因此,把uy和uλ的初值设为0,继续化简可得

注1从式(3)中可以看出,函数g的邻点映射与关于S的投影映射是分开计算的.文献[13]中的Algorithm 5需要计算函数gi+的邻点映射,其中为集合Si的示性函数.因此,当分开计算相较于合起来计算更容易时,式(3)更为适用.此处所指为可以得出具体表达式的情形,而省去解决一个优化子问题.例如,令P表示{1,...,m}的一个划分,x:(ˇx,t)∈Rm-1×R,函数g(x):其中,x[p]表示对应p的分量.根据文献[20,§6.5.4],可以计算g(x)的邻点映射为

注2得益于FRDR算法的特性,式(3)所代表的算法,其收敛不需要假设伪梯度映射是强单调的或协强制的.后续将会给出证明.

式(3)的伪代码如算法1所示.

定理1在假设1-5均成立的情况下,若β ＞0,且0＜γ ＜β/(1+2ϱβ),则有算法1中的xk收敛到v-GNE.

证

步骤1首先,证明wk收敛到zer(G+B+).

由假设1可知,G和N˜˜S都是极大单调的;由假设3和假设4可知,B是极大单调的;由假设5以及F和C的定义可知,B是ϱ-Lipshitz连续的,其中ϱρ+µmax+‖C‖.根据文献[17]中的定理5.1可得,wk收敛到zer(G+B+).

步骤2然后,证明xk收敛到v-GNE.

根据引理1,由wk收敛到zer(G+B+)可得,xk收敛到v-GNE.

证毕.

注3算法1之所以叫作半分布式,是因为当目标函数依赖于所有智能体的xi时,获取全部的信息需要通过中心结点来实现;而当其仅受邻居影响时,该算法就是分布式的.无论如何,对偶变量λi的信息总是通过分布式的方式获取.所以,采用半分布式来命名该算法.

注4从算法1中可以清楚地看到,每个智能体通过存储上一轮收集到的信息,从而实现了每一轮迭代中只进行一次信息交换.另外,也可以将上一轮计算的伪梯度信息存储下来,这样的话,每一轮迭代只需要计算一次伪梯度.

尽管算法的收敛速率并未在文献[17]中直接给出,但是根据其定理5.1的证明可推出如下结论.

推论1对于式(2)所产生的序列{(wk,uk)},有如下关系成立:

证令

根据文献[19]中的引理1第4部分可得

利用范数的等价性.证毕.

4 数值仿真

考虑由编号1,...,21共21个公司(智能体)和编号M1,...,M6共6个市场组成的网络化古诺博弈,其网络结构如图1所示,其中圆形表示公司,方形表示市场,箭头表示公司向市场供应产品.智能体之间的通信连接如下图2所示.

图1 网络化古诺博弈的网络结构Fig.1 Structure of networked Cournot game

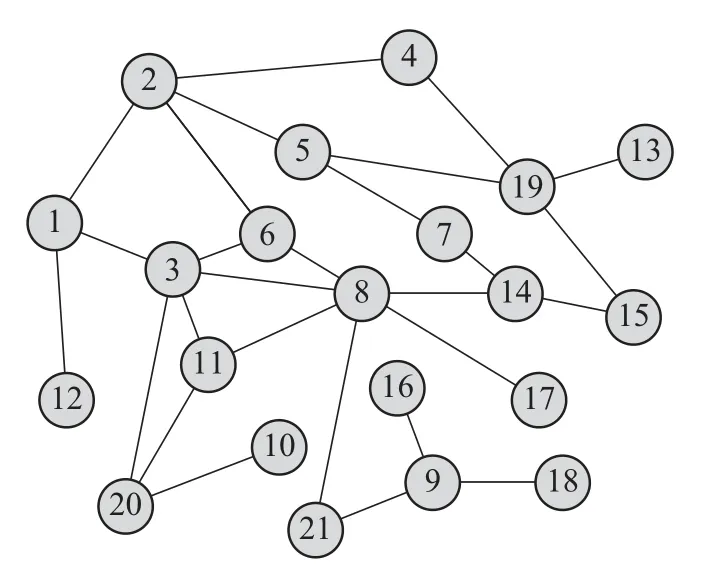
图2 智能体之间的通信拓扑Fig.2 Communication topology between agens

给定目标函数为

图3-5分别表示迭代残差,一致性误差和约束残差的变化趋势.从图3-5中可以看出,迭代残差和约束残差以及一致性误差都呈现出减小的趋势,说明{xk}是逐渐收敛的且趋向于约束集合,同时{λi,k}逐渐达到一致.

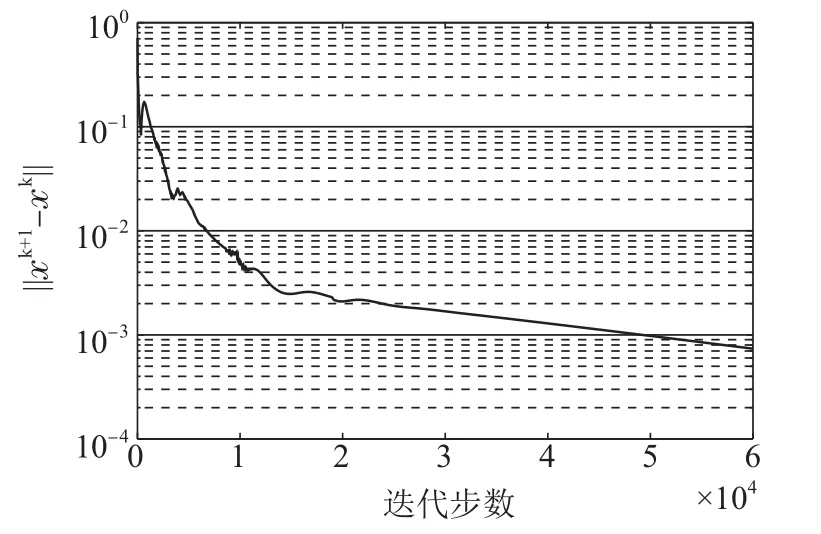
图3 迭代残差Fig.3 Iteration residual

5 结论

本文基于三算子分裂算法forward-reflected-Douglas-Rachford(FRDR)算法,提出一种半分布式的FRDR算法.该算法有如下特性: 可以实现邻点映射和投影映射分别进行计算,因此在计算上更适用于分开计算简单而合起来计算困难的情形;而且不需要假设伪梯度映射是协强制的或者强单调的;通过存储上一轮交换的信息,可以做到所需信息在每一轮迭代中只进行一次交换.此外,数值仿真验证了所提算法的有效性.

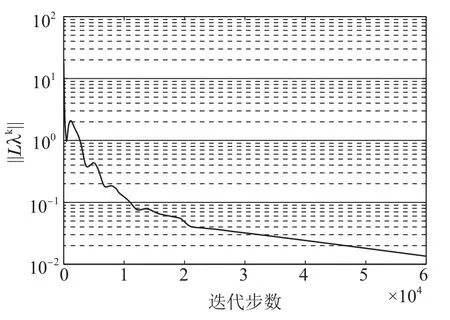
图4 一致性误差Fig.4 Consensus error

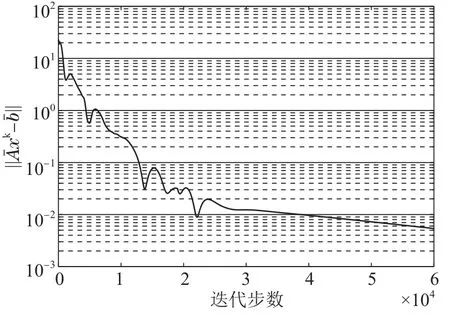
图5 约束残差Fig.5 Constraint residual